基于二次方程组的邻近圆轨道四冲量最优交会*

陈长青，解永春

（1.北京控制工程研究所，北京100190；2.空间智能控制技术国家级重点实验室，北京100190）

基于二次方程组的邻近圆轨道四冲量最优交会*

陈长青1，2，解永春1，2

（1.北京控制工程研究所，北京100190；2.空间智能控制技术国家级重点实验室，北京100190）

研究了一种基于二次方程组的邻近圆轨道四冲量最优交会的求解方法.给出邻近圆轨道交会的无量纲化动力学方程及相应的基向量方程，介绍由Carter提出的一种基于二次方程组的四冲量最优交会的求解方法，在提出邻近圆轨道最优冲量交会的原始解、相反解、对偶解、对偶相反解概念的基础上，分析基于二次方程组的四冲量最优交会的求解方法存在的问题，并给出修正方法.仿真结果表明，该方法是对Carter提出的基于二次方程组的四冲量最优交会求解方法的有效补充.

邻近圆轨道；四冲量最优交会；二次方程组

在交会对接过程中，对燃料消耗的优化一直是国内外学者研究的热点.20世纪60年代末，Prussing关于邻近圆轨道有限时间内多冲量最优交会理论是其间很突出的成果.Prussing［1-2］针对邻近圆轨道平面交会问题，选择两圆形轨道的中间轨道建立参考坐标系，利用线性方程下共轭变量与状态变量的解耦性，分别对基向量和边界值问题进行求解，得到具体交会时间和初末相对状态下最优冲量模式的分布情况.在Prussing［1-2］的工作基础上，国内外不少学者对该理论进行了补充和延伸：文献［3］选择平均速率参考轨道，重复了Prussing的工作，使得交会结束后参考系原点与目标航天器重合，同时提高了追踪航天器与目标航天器存在较大初始相位差时的交会精度；文献［4］和［5］研究了具体轨道下不同交会时间的三冲量最优交会模式；文献［6］以目标航天器轨道为参考轨道，研究邻近圆轨道的最优冲量交会问题，分析了不同交会模式的边界分布情况；文献［7］针对四冲量求解问题，提出了一种基于二次方程组的求解方法，大大提高了求解的效率.

但是文献［7］提出的求解方法，在某些存在四冲量最优解的交会问题中无法得到正确解.本文在文献［7］的研究基础上，提出原始解、相反解、对偶解、相反对偶解的概念，分析文献［7］中求解方法无法得到正确解的原因，并给出一套完整的基于二次方程组的四冲量最优交会的求解方法.

1 动力学方程和基向量方程

如图1所示，追踪航天器和目标航天器均沿圆轨道运动，其初始相位角之差为β，O点为地球球心，选择中间轨道为参考轨道，参考坐标系的初始原点在地心与追踪航天器连线的延长线上，利用如下无量纲化的线性方程研究航天器相对参考圆轨道的平面内相对运动［1-2］：

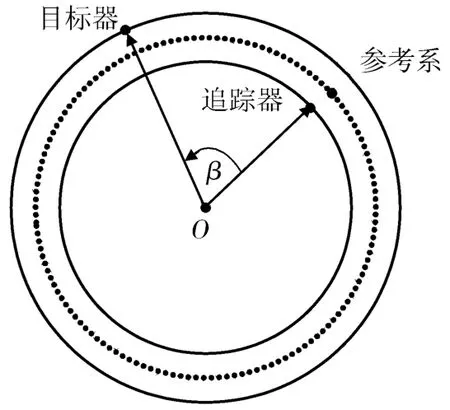
图1 相对运动与参考轨道

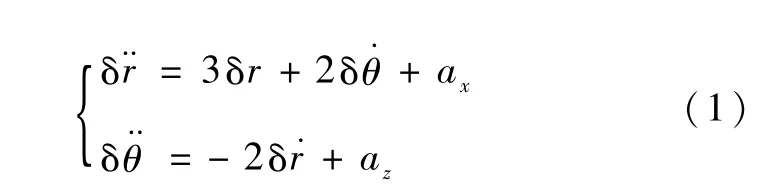
式中，归一化后的参考圆轨道的轨道半径为1，δr为航天器与参考轨道的半径差的归一化表示，δθ为航天器与参考系原点的相位角之差，以飞行方向为正向，ax和az分别为径向和切向归一化后的推力加速度.方程（1）中的导数都是相对于无量纲化后的时间τ求得的.记则方程（1）写成状态方程的形式如下：

方程（2）的状态转移矩阵为

式中τ为归一化后的转移时间.对于邻近圆轨道交会问题，交会时间为τF时，初末相对状态为

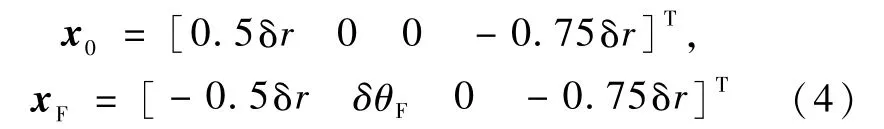
式中δθF＝β－0.75τFδr.定义基向量p＝－λv＝［λμ］T，其中λv为状态变量的共轭变量，利用最优控制理论可以得到基向量方程为［1-2］

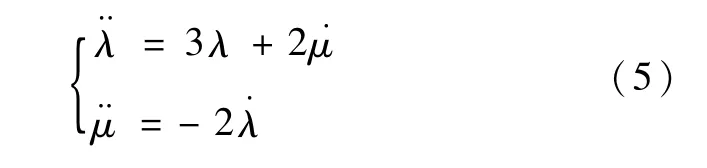
可以求得方程（5）的解为

式中参数A，B，C为待定常数.

本文将利用方程（1）、（2）、（5）描述邻近圆轨道的交会活动，研究文献［7］提出的基于二次方程组的四冲量最优交会的求解方法.

2 基于二次方程组的邻近圆轨道四冲量最优交会

本文只给出一些关键的推导过程，分3部分进行阐述，具体的求解过程参见文献［7］.

（1）基向量解的简化表示

由最优交会的必要条件可以得到当四脉冲最优交会成立时基向量满足对称性、相交条件和相切条件［1，7］.利用对称性分析式（6）中的参数，可以得到

引入新的变量

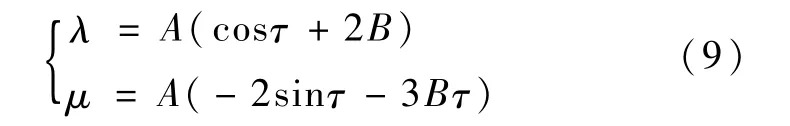
（2）基向量方程的求解

下面基于式（9），利用二次方程组来求基向量解的相关参数.通过相切条件可以得到

式中β（τ3）和γ（τ3）的表示与文献［7］中式（40）和式（41）相同.利用相交条件可以得到

式中δ（τ3，τ4）和η（τ3，τ4）的表示与文献［7］中式（48）和式（49）相同.

在已知交会时间τF的条件下，可以得到τ4＝τF／2，则由式（12）可以求得含τ3，τ4的B

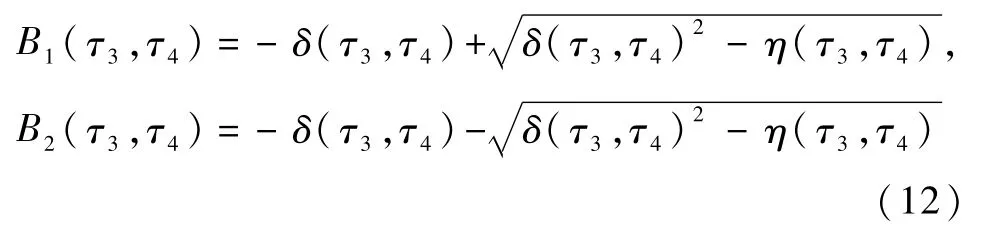
把式（12）代入式（11）可以得到方程（13）是两个只含有τ3的二元一次方程，容易求解得到τ3.将τ3代入方程（12）可以得到B.由基向量模值等于1可以求得

由对称性容易求得

则4个冲量时刻为

（3）边界值问题的求解

当初末相对状态由式（4）表示时，可以利用边界值求解问题得到4个冲量幅值.记

又记Gi＝Φ（τi－τ1）B pi，则进一步可以求得4个冲量幅值如下：

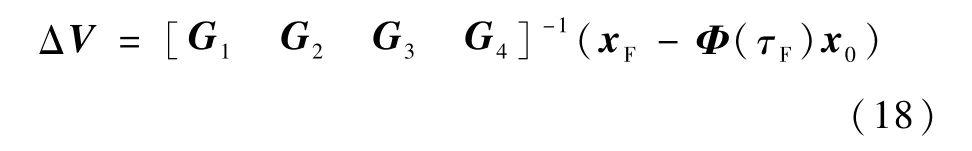
式（17）中i＝1，2，3，4.若ΔV中的4个分量均不小于0，则存在四冲量解，4个冲量时刻由式（16）决定，冲量方向由式（17）确定，冲量大小由式（18）确定.

3 邻近圆轨道交会中的原始解、相反解、对偶解和对偶相反解

在文献［7］中，Carter利用简化的基向量解方程（9），通过解二次方程组来求解四冲量最优基向量解，大大简化了求解过程.但是对于某些满足四冲量最优交会的问题，利用该方法可能无法得到正确解.下面从基向量方程出发，根据基向量解中的原始解、相反解、对偶解和对偶相反解，分析无法得到正确解的原因；根据边界值问题中的原始解、相反解、对偶解和对偶相反解，探讨无法得到正确解满足的初末相对状态和交会时间.

3.1 基向量解中的原始解、相反解、对偶解和对偶相反解

对方程（5）进行分析，可以推导得到关于基向量的两个方程

式中，第一个方程只存在奇次导数项，第二个方程只存在偶次导数项.显然若有λ（τ）满足方程（19），则必有λ（－τ）也满足方程（19）；同样若有μ（τ）满足方程（19），则必有μ（－τ）也满足方程（19），即若方程（19）存在如下原始解：

则必然存在分别由方程（21）、（22）、（23）表示的相反解、对偶解和对偶相反解

这3组解的参数与原始解的参数之间存在如下关系：

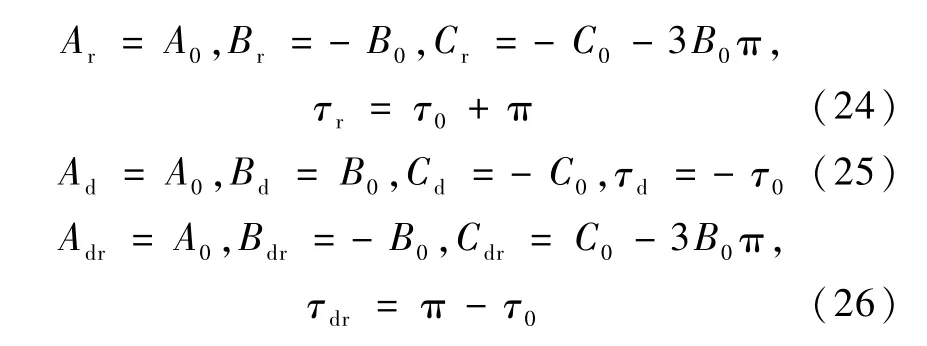
对于四冲量最优交会问题，若原始解冲量时刻的4个相位角为τ1，τ2，τ3，τ4，且四冲量最优交会问题存在式（15）所示的对称性，则对偶解冲量时刻的相位角同样也可以表示成τ1，τ2，τ3，τ4.类似的，相反解和对偶相反解冲量时刻的相位角可以表示成π＋τ1，π＋τ2，π＋τ3，π＋τ4.

式（7）中当n＝0时，C0＝0，原始解和对偶解可以由式（9）求得.当n为其他偶数时，由式（9）可以很容易得到原始解和对偶解，其四冲量解与n＝0时的解一样.显然通过文献［7］的方法可以求得原始解和对偶解.当C0＝0，n＝1时，可以验证由式（21）、式（24）确定的相反解和由式（23）、式（26）确定的对偶相反解，变换A，B，τ后同样可以写成式（9）的形式.当n取不等于1的其他的奇数时，类似的，经过变换，相反解和对偶相反解也可以写成式（9）的形式，但是通过式（9）求得系数A，B后需要做相反的变换，否则得不到相反解和对偶相反解.文献［7］中的方法没有进行相反变换，所以无法得到这两组解.

3.2 边界值问题中的原始解、相反解、对偶解和对偶相反解

若有一组最优交会解满足相对高度差为δr0，初始相位角差为β0，δθF0＝β0－0.75τFδr0.记这组最优交会解为原始解，其冲量方向为（λ01，μ01），…，（λ0n，μ0n），冲量幅值为ΔV01，…，ΔV0n；对应的相反解的冲量方向为（－λ01，－μ01），…，（－λ0n，－μ0n），冲量幅值为ΔV01，…，ΔV0n，相反解对应的交会问题满足δrr＝－δr0，βr＝－β0，δθFr＝－δθF0；对应的对偶解的冲量方向为（λ0n，－μ0n），…，（λ01，－μ01），冲量幅值为ΔV0n，…，ΔV01，对偶解对应的交会问题，其高度差与原始解互为相反数，即δrd＝－δr0，初始相位角差为βd＝β0－1.5τFδr0，且有δθFd＝βd－0.75τFδrd＝δθF0；对应的对偶相反解的冲量方向为（－λ0n，μ0n），…，（－λ01，μ01），冲量幅值为ΔV0n，…，ΔV01，对偶相反解对应的交会问题满足δrdr＝δr0，βdr＝－β0＋1.5τFδr0，δθFdr＝－δθF0.表1给出了这4组解之间的关系.

表1 边界值问题中原始解、相反解、对偶解、对偶相反解之间的关系

从以上分析可以看出对于同一个交会时间，存在4组解，且当它们分别对应于不同的轨道高度差和初始相位角差时，它们的冲量方向与冲量幅值存在一定的关系.文献［7］的方法只能得到原始解和相反解，而当边界值问题中的初末相对状态满足对偶解和对偶相反解时无法得到正确解.

3.3 四冲量最优交会中的原始解、相反解、对偶解和对偶相反解

在文献［7］中，对于一个具体的交会时间τF，可以利用求解二次方程组的方法求得4个冲量时刻的相位角.由于四冲量最优交会解具有对称性，所以原始解和对偶解的相应冲量时刻的相位角是一致的.可以从利用文献［7］的方法，通过求解边界值，求得原始解和对偶解.

当边界值问题中的初末相对状态满足相反解和对偶相反解时，无法用文献［7］中的方法求得相反解和对偶相反解，这时需要增加对相反解和对偶相反解的判断求解，即从方程（24）、方程（26）求得相反解和对偶相反解的系数，再利用边界值问题进行判断求解.

4 仿真分析

考虑邻近圆轨道的交会问题，若目标器轨道高度为400 km，追踪器轨道高度为360 km，选择中间轨道为参考轨道，则有Rr＝6 758.14 km，可以计算得到δr＝0.005 919，τ4＝5.145，τ3＝2.134，B＝0.370 1，交会时间为905 4s，即τF＝10.29.

当追踪器和目标器的初始相位角之差为1°，即β＝0.017 45 rad时，初末相对状态分别为x0＝［－0.002 959 0 0 0.004 439］T，xF＝［0.002 959－0.045 57 0 －0.004 439］T，则可以求得满足四冲量最优交会的4个冲量幅值为［13.998 13.550 2.180 2.133］Tm／s.由于四冲量最优交会的对称性，当βd＝－0.073 9 rad，δr＝0.005 919时，同样可以求得这个交会问题的4个冲量幅值为［2.133 2.180 13.550 13.998］Tm／s.这两组解分别为原始解和对偶解.

当两个航天器的轨道高度与原始解的轨道高度相反，且相位角差为－β＝－0.017 45 rad时，利用文献［7］的方法求得的4个冲量幅值为［－13.998－13.550 －2.180 －2.133］Tm／s，显然不满足四冲量最优交会.而实际上相反解可以满足该交会问题.由式（24）有B＝－0.370 1，C＝－3.488，τr＝π＋τ0，可以得到冲量幅值为［13.998 13.550 2.180 2.133］Tm／s，可以验证该解满足四冲量最优交会的必要条件.同样当轨道高度为δr＝0.005919，初始相位角差为βdr＝0.073 9 rad时，由文献［7］的方法可求得冲量幅值为［1.405 1.089－21.198 13.080］Tm／s，显然不满足四冲量最优解.而对偶相反解满足该交会问题，利用式（26）重新计算，可得到冲量幅值为［2.133 2.180 13.550 13.998］Tm／s，可以验证该解满足四冲量最优交会的必要条件.

从上面的仿真和分析可以看出，文献［7］中提出的方法遗漏了相反解和对偶相反解，而本文对基向量解的补充修正，增加了对这两组解的计算，防止了解的遗漏，完善了基于二次方程组的四冲量最优交会的求解方法.从仿真还可以看出，所遗漏的两组解其参数B与原始解的相应参数互为相反数，漏解的原因是在基向量解简化表示过程中，当n为奇数时，解的形式实际上已经发生变化，所以利用文献［7］的方法求解基向量后，需要对该形式进行还原.本文对相反解、对偶相反解的判断求解，实际上就是对n为奇数时的还原求解.

5 结 论

Carter针对Prussing的邻近圆轨道最优交会理论，提出了一种基于二次方程组的四冲量最优交会的求解方法，大大简化了求解过程，但是在某些情况下无法得到正确解.本文在前人研究的基础上，给出了原始解、相反解、对偶解、对偶相反解的概念，完善了Carter的四冲量最优交会求解方法，并指出原始解和对偶相反解的存在是最优交会模式对称的根本原因.仿真结果表明，本文的工作是对文献［7］提出方法的有效补充，进一步完善了邻近圆轨道最优冲量交会理论.

［1］ Prussing JE.Optimal four-impulse fixed-time rendezvous in the vicinity of a circular orbit［J］.AIAA Journal，1969，7（5）：928-935

［2］ Prussing JE.Optimal two and three-impulse fixed-time rendezvous in the vicinity of a circular orbit［J］.AIAA Journal，1970，8（7）：293-310

［3］ Liu F C，Plexico L D.Improved solution of optimal impulsive fixed-time rendezvous［J］.Journal of Spacecraft and Rocket，1982，19（6）：521-528

［4］ Qi Y H，Cao X B.Optimal rendezvous trajectory planning with time constraint［C］.1stInternational Symposium on Systems and Control in Aerospace and Astronautics，Harbin，2006

［5］ 齐映红，曹喜滨.三脉冲最优交会问题的解法［J］.吉林大学学报（工学版），2007，36（4）：608-612

［6］ 陈长青，解永春.参考系在目标器轨道的邻近圆轨道最优脉冲交会研究［J］.载人航天，2007，25（3）：16-19

［7］ Carter T E，Alvarezs A.Quadratic-based computation of four-impulse optimal rendezvous near circular orbit［J］.Journal of Guidance，Control and Dynamics，2000，23（1）：109-117

Quad ratic-Based Computation of Four-Impulse Optimal Rendezvous between Near Circular Orbits

CHEN Changqing1，2，XIE Yongchun1，2
（1.Beijing Institute of Control Engineering，Beijing 100190，China；2.Nationalkey Key Laboratory of Science and Technology on Space Intelligent Control，Beijing 100190，China）

In this paper，a method of solving quadratic equations-based four-impulse optimal rendezvous between near circular orbits is investigated.Dimensionless dynamics equations for rendezvous between near circular orbits and their corresponding primer vector e-quations are introduced.And the method of quadratic equations-based four-impulse optimal rendezvous presented by Carter is explained.Then four concepts including original solution，reciprocal solution，dual solution and dual reciprocal solution of rendezvous between near circular orbits are given.By using these concepts the problems of solving quadratic equations-based fourimpulse optimal rendezvous are analyzed，and amodifying method is given.The simulation results show that the modifying method is a good supplement for the method of quadratic equations-based four-impulse optimal rendezvous.

near circular orbit；four-impulse optimal rendezvous；quadratic equations

V526

A

1674-1579（2009）06-0045-05

*国家自然科学基金资助项目（90305024）.

2009-04-07

陈长青（1979—），男，福建人，工程师，研究方向为交会对接的制导技术（e-mail：changqingchen＠hotmail.com）.