空间机器人动力学建模与模型验证*

张 军，胡海霞

（1.北京控制工程研究所，北京100190；2.空间智能控制技术国家级重点实验室，北京100190）

空间机器人动力学建模与模型验证*

张 军1，2，胡海霞1，2

（1.北京控制工程研究所，北京100190；2.空间智能控制技术国家级重点实验室，北京100190）

建立带任意节机械臂的空间机器人动力学模型，并验证了模型的正确性.采用Kane方程建立了各体间转铰具有三自由度的空间多体系统的动力学模型，利用投影算子将所建立的模型退化为各节机械臂间具有单自由度转铰连接的空间机器人动力学模型，依据动力学三大基本定理，即动量定理、动量矩定理、动能定理设计了模型验证方案，通过数学仿真验证了所建立模型的正确性.

空间机器人；动力学建模；Kane方程

符号表

上标× 列阵的反对称阵

t 当前时间

x｜t＝0变量x的初值

n 机械臂的节数

N 描述系统自由度的变量的个数

i 空间机器人各体的编号，取0时代表基座

p 广义坐标变量的编号，取值1，2，…，N

Fe惯性坐标系oexeyeze

Fii体的本体坐标系oixiyizi，oi取i体与第i－1体的铰接处，i＝0时oi为基座上任意点

Eii体的动能

mii体的质量

e Fe的3轴单位方向矢量

biFi的3轴单位方向矢量

Ae，i从Fi到Fe的坐标转换矩阵

Aij从Fj体到Fi的坐标转换矩阵

qi单自由度转铰连接情况下第i节机械臂相对i－1节机械臂的转角

ii

Sijj体相对oi的静矩

Jijj体相对oi的转动惯量系统所受总的外力

M→ii～n体所受外力相对oi的力矩与i～n体所受外力矩之和

空间机器人由卫星基座及搭载的机械臂组成，主要用于在轨服务，包括自主交会对接、失效卫星的抢救及零部件安装与更换等.随着国际空间站［1］、ETS-Ⅶ［2］、XSS-10［3］、XSS-11［4］、“轨道快车”［5］的相继发射，空间机器人正成为人类开发利用太空资源的重要手段.相对于地面固定基座的机器人，空间机器人具有漂浮基座，卫星本体与机械臂的运动相互耦合，其动力学特性更复杂［6］.对空间机器人进行动力学建模并确保模型的正确是控制系统设计与方案设计的基础.

尽管已有的成熟商业化软件（如ADAMS）能进行多体系统的建模，并在前期工作中可用于系统的初步动力学分析，但为进行控制系统的设计及详细的动力学分析，建立空间机器人模型的显式无疑是基本的，目前对空间机器人建模的主要方法包括Lagrange方程法［7］、虚拟机械臂法［8］、等价机械臂法［9］、广义Jacobian矩阵法等［10］.采用Lagrange方程建模，需要对Lagrange函数进行二阶求导，计算非常复杂；采用虚拟机械臂方法建模时，首先假设在系统质心相对惯性系铰接，然后采用固定基座机器人的建模方法建模；等价机械臂继承虚拟机械臂的建模方法，将空间机器人的模型与地面机器人的模型进行等价转换；广义Jacobian矩阵法本质上采用的是New ton-Euler法.上述方法都是将系统的质心平动与转动解耦，而空间机器人实际上是变惯量系统，物理上并不存在与系统质心对应的确定的点.实际任务操纵及控制系统设计时，人们常要关心系统上确定位置的运动状态，如交会对接过程中就要考虑卫星基座上交会测量相机的运动状态，如果采用上述方法建模，则需要将系统质心的位置变化转化为相机的位置变化，然后再设计相应的控制策略.

与上述方法不同，本文采用Kane方程建立空间机器人的动力学模型，尽管各种多体动力学建模方法都很复杂，但采用Kane方程建模，过程烦而不难，并且Kane方程采用卫星基座上任意一点（而非系统质心）的平动及各体间的相对转动来描述整个系统的运动状态，物理意义明确，所建立的动力学模型可直接用于控制系统的设计.

此外，从工程的角度，针对目前文献都没有对所建立的模型进行验证的问题，本文利用动力学三大基本定理，即动量定理、动量矩定理、动能定理，对所建立的模型设计了验证方案，通过数学仿真验证了所建立模型的正确性.

1 基于Kane方程的动力学建模

从结构上来看，空间机器人是具有漂浮基的多体树形系统，其拓扑结构如图1所示.不失一般性，这里只考虑单只机械臂的情况，含多只机械臂的动力学模型可以很容易地由单只机械臂的情况演化得到.

图1 空间机器人的树形拓扑结构

1.1 机械臂的运动描述

dmi的加速度为

1.2 广义坐标的选取与系数矩阵的确定

为了用Kane方程对空间机器人进行建模，将系统中各点的速度表示成如下形式：

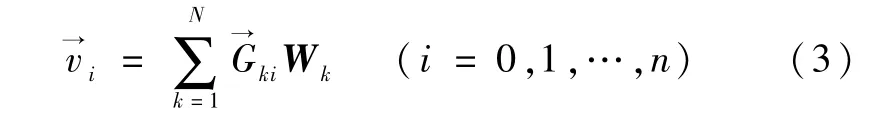
式中，Wi为系统的广义速度，为相对Wi的系数矩阵表示其元素为矢量.

对空间机械臂取广义速度

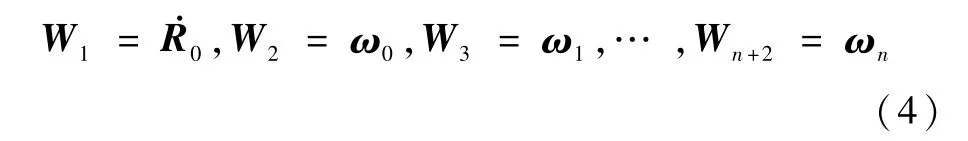
根据式（1）和式（3）可得

1.3 动力学方程的建立

暂不考虑系统中的挠性部件，则系统弹性势能为0，由Kane方程知，相对第p个广义坐标的动力学方程可由下式得到：

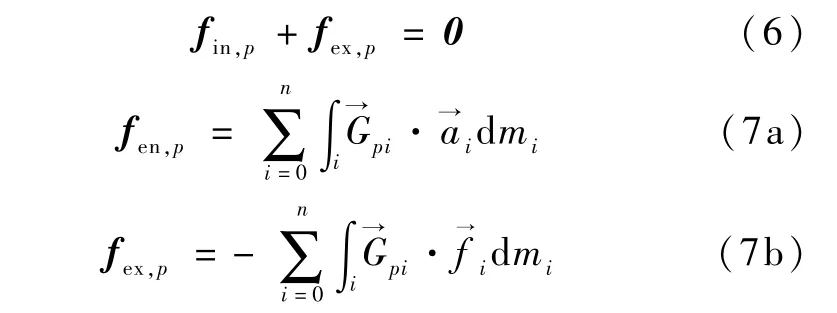
式中，fen，p为广义惯性力，fex，p为广义外力为作用在i体上的分布式系统外力［11］.

对于空间机器人，不考虑空间环境干扰力矩时，系统所受力与力矩不是分布式的，为集中力或集中力矩，不需用上面式子中的积分就可直接得到各阶广义外力.则由式（6）和式（7）可得到关于、ω0、ωi的动力学方程分别为

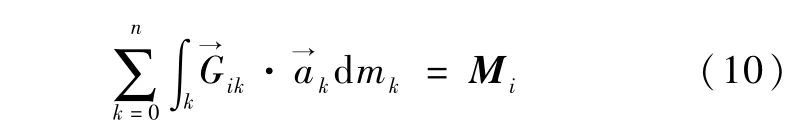
将式（2）和式（5）代入式（8）～（10），经过推导可得到关于、ω0、ωi的动力学方程，进而得到如下形式的系统动力学方程：

式中，

式（11）建立的动力学模型中各体间具有3个转动自由度，而一般空间机器人各节机械臂只具有单自由度.不失一般性，这里假设该单自由度沿Fi的zi方向，此时空间机器人动力学模型可由式（11）经过投影算子变形得到

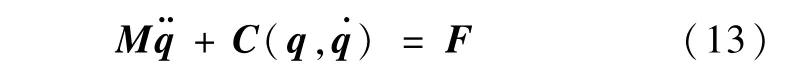
式中，

P为Fi中在zi上的投影算子.

2 模型验证方案

理论上采用成熟方法建立的动力学模型都是正确的，但由于空间机器人动力学模型十分复杂，所以必须对所建立的动力学模型进行验证，实践也证明，未进行验证和修正的模型常常存在错误，而其导致的后果则是灾难性的.对模型的验证可采用两种方法：一种是与采用另外方法（如商业化软件ADAMS等）建立的模型进行仿真结果的比对；另一种是采用物理定律进行验证.采用第一种方法时，首先需要另外建立一套模型，而在相同的输入与参数设置下，一旦两套模型输出不一致，进行问题定位就非常困难，因此是一种理论上简单而实际操作比较困难的方法.

本文采用第二种方法，利用动力学系统三大基本定理，即动量定理、动量矩定理、动能定理，对模型进行验证，只要所建立的模型在任意参数设置与任意输入下，始终满足三大基本定理，就认为所建立的模型是正确的.不同的参数与不同的输入可以暴露空间机器人各子体的运动特性，因此验证方案均针对整个空间机器人系统设计.

2.1 动量定理验证方案

动量定理描述的是系统质心的线运动规律.对于任意一个动力学系统，其质心的运动规律由所受的外力决定，与系统内力及内外力矩无关，其运动规律满足牛顿第二定律.

定义j体相对oi的静矩Sij：

可得系统质心在F0中坐标为

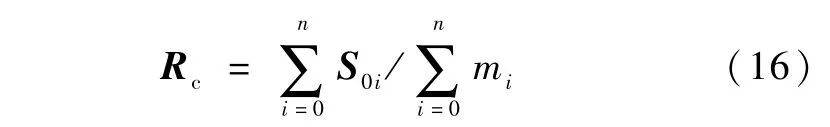
则系统质心在Fe中的坐标可表示为

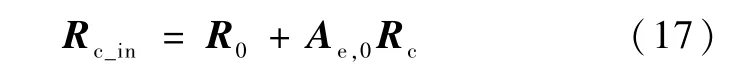
由牛顿第二定律可知

2.2 动量矩定理验证方案

i体的质心相对Fe的线速度在Fe中的坐标可表示为

i体的质心相对系统质心的矢量在F0中的坐标可表示为

则系统总的角动量为

式中：Mom1为系统各体由于平动导致的相对系统质心的角动量；Mom2为各体由于转动导致的角动量.

j体上外作用力相对oi的矢量坐标为

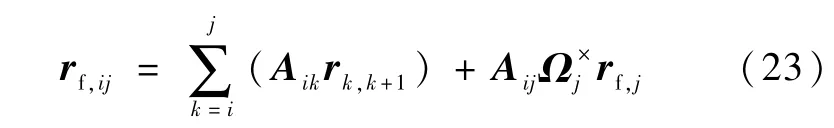
相应外力在Fi中的坐标为

则动力学方程中与各体相应的外力矩可表示为

系统所受相对系统质心的总的外力矩可表示为

由动量矩定理，系统应始终存在如下等式关系：

积分号上标tnow表示当前时间。

2.3 动能定理验证方案

系统总的动能为

式中

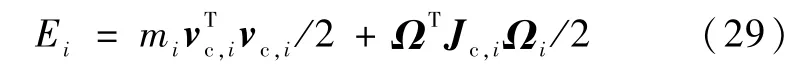
外力与外力矩作用的功为

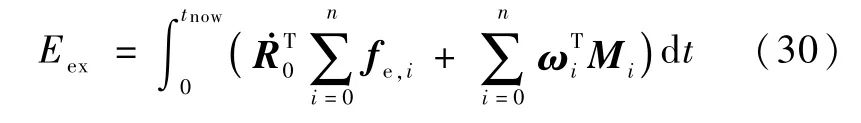
由动能定理，系统应始终存在如下等式关系：

3 数学仿真

针对所建立的空间机器人动力学模型与验证方案，采用Matlab／Simulink进行数学编程，建立空间机器人仿真系统，下面给出一组仿真算例.

仿真中假设空间机器人有6节机械臂，此时机械臂末端可以以任意姿态定位在空间中任意点.

一般来讲，空间机器人的机械臂质量及惯量值要远小于基座本体，但在进行模型验证时，为了放大机械臂的动力学影响，仿真中将机械臂的质量及惯量参数设成与基座的同等量级，其中各体相对其质心的转动惯量及质量取为Jc5＝1．2Jc0，Jc6＝0．8Jc0，m0＝440kg，m1＝350kg，m2＝300kg，m3＝280kg，m4＝260kg，m5＝320kg，m6＝340kg.下面的仿真中，为了具有一般性与代表性，在空间机器人各体上都施加外力与外力矩，具体值由Matlab随机生成，记Me＝，rf，取值：

在10s≤t≤30s时，外力与外力矩取式（31）中各值；在40s≤t≤60s时，外力与外力矩反向，但值保持不变；其余时间内外力与外力矩取0.空间机器人初始状态为在惯性空间中静止，各变量初始值取0.图2为星体基座的三轴角速度与欧拉角，从图中可以看到，前10s基座处于静止状态，从第10秒开始，基座出现非零角速度，至到仿真结束；图3为6节机械臂的6节关节角，也是从第10秒开始出现运动，至到仿真结束；图4中给出的是空间机器人系统质心的速度与受到的总外力曲线，由于外力在10s≤t≤30s及40s≤t≤60s中都是常值，因此系统质心在惯性空间中先后分别作匀加速与匀减速运动，60s后系统质心重新处于静止状态，其运动规律符合动量定理；图5（a）中给出空间机器人的角动量曲线，图5（b）中给出的曲线为将仿真中外力撤除后，即只作用Me时空间机器人的角动量曲线，图5（a）中第60秒后，系统存在残余角动量，而图5（b）中第60秒后，系统角动量完全为0，因为在惯性空间中前后两段时间外力矩作用的大小相等、方向相反，则最后系统的总角动量必然为0；图6则为与图5相对应的系统的总动能；在图7和图8中给出了在Simulink下设置不同的相对容许误差，容许误差为式（27）与式（31）中等号左边项减去右边项后的值，图（a）、（b）、（c）分别将容许误差设为10－9、10－12、10－15，从仿真曲线可以看到，式（27）与式（31）左右两项相减后的残差随着设置的容许误差的减小而减小，因此可认为仿真中式（27）与式（31）的左右两边是完全相等的，相减后的残差由仿真误差引起，即动量矩定理与动能定理得到了验证.

图2 基座3轴角速度与欧拉角

图3 6节机械臂的相对转角

图4 系统的质心速度与所受总的外力

图5 系统的3轴总角动量

图6 系统的3轴总动能

除了上述仿真算例，还采用其他输入条件与参数进行了各种数学仿真，也都得到了与上述一致的仿真结果，证明了所建立的模型都能满足所设计的模型验证方案.条件成熟后，还采用相同的输入与初始条件，与NASDA进行ETS-7方案论证时采用的模型进行了仿真结果比对，结果完全一致，也进一步证实了本文所建模型及验证方案的正确性.

4 结 论

采用Kane方程建立了空间多体系统的动力学模型，利用投影算子将所建立的动力学模型退化为采用单自由度铰接连接的空间机器人动力学模型，接着依据动力学三大基本定理，即动量定理、动量矩定理、动能定理设计了模型的验证方案，通过仿真验证了所建立的动力学模型的正确性及验证方案的有效性.本文建立的空间机器人的动力学模型采用卫星基座上固定点的平动及相邻体间的转动运动来描述系统的状态，物理意义明确，特别适合于空间机器人的任务规划及控制系统的设计.

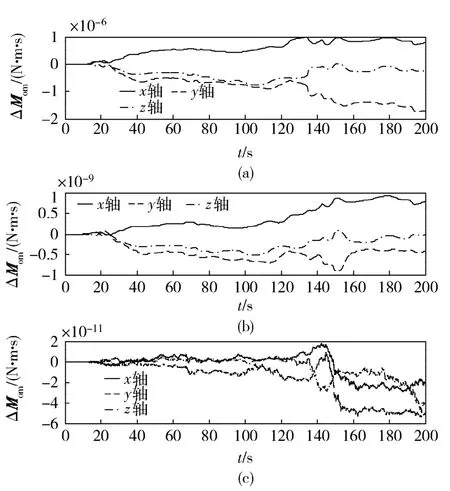
图7 不同容许误差下的角动量仿真误差

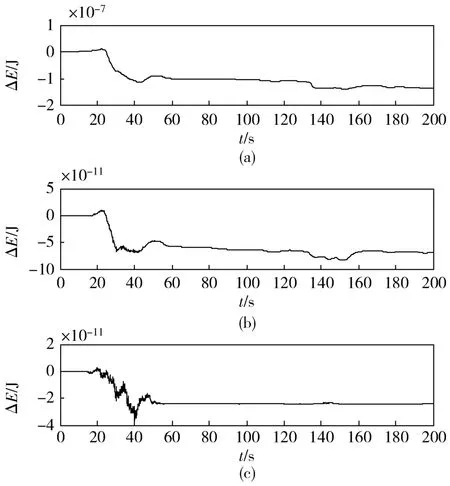
图8 不同容许误差下的动能仿真误差

［1］ Mah H W，Modi V J.A relatively general formulation for studying dynamics of the space station based arms with applications［R］.AIAA-88-0674，1988

［2］ Oda M.On the Dynamics and control of ETS-7 satellite and its robot arm［C］.The IEEE／RSJ／GI International Conference on Intelligent Robots and Systems，Tokyo，Japan，1994

［3］ Barnhart D A，Hunter R C，Weston A R，et al.XSS-10 micro-satellite demonstration［R］.AIAA-98-5298，1998

［4］ 闻新，王秀丽，邓宝忠.美国试验小卫星XSS-11系统［J］.中国航天，2006（7）：22-25

［5］ Shanes，Pejmun M.Orbital express capture system：concept to reality［C］.SPIE，Bellingham，WA，USA，2004

［6］ Dubowskys，Papadopoulos E.The kinematics，dynamics and control of free-flying and free-floating space robotics systems［J］.IEEE Transactions on Robotics and Automation，1993，9（5）：531-543

［7］ Papadopoulos E，Dubowskys.On the nature of control algorithms for free-floating space manipulators［J］.IEEE Transactions Robotics and Automation，1991，7（5）：750-758

［8］ Vafa Z，Dubowskys.On the Dynamics of space manipulator using the virtual manipulator with application to path planning［J］.The Journal of the Astronautical Science，1990，38（4）：441-472

［9］ 梁斌，刘良栋，李庚田.空间机器人的动力学等价机械臂［J］.自动化学报，1998，24（6）：761-767

［10］ Umetani Y，Yoshida K.Resolved motion rate control of space manipulators with generalized Jacobian matrix［J］.IEEE Transactions on Robotics and Automation，1989，5（3）：303-314

［11］ 黄文虎，邵成勋.多柔体系统动力学［M］.北京：科学出版社，1996：53

［12］ 张军.空间机器人动力学建模与仿真验证［R］.北京控制工程研究所，2007

Dynamics Modeling and Simulation Verification for Space Robot

ZHANG Jun1，2，HU Haixia1，2
（1.Beijing Institute of Control Engineering，Beijing 100190，China；2.National Key Laboratory of Science and Technology on Space Intelligent Control，Beijing 100190，China）

The dynamicsmodel of a free-flying space robotwith arbitrary joints connected manipulator is established，and verified by numerical simulation.Firstly，the model of a space multi-body system with three degrees of freedom in adjacent bodies is established using Kane equation.Then，projective operators are used to transform general equations into the dynam icsmodel of a space robot with one degree of freedom between the bodies of itsmanipulator.Three fundamental dynamical theorems，i.e.momentum theorem，momentum moment theorem，kinetic energy theorem are used to design the algorithm to verify the dynamicsmodel.Finally，numerical simulation verifies the dynamicsmodel of the space robot.

space robot；dynamicsmodeling；Kane equation

*国家自然科学基金（10872028）资助项目.

2009-04-07

张 军（1980—），男，湖北人，工程师，研究方向为空间站、空间机器人及在轨服务GNC技术（e-mail：zhangjun10＠gmail.com）.

TP24

A

1674-1579（2009）06-0006-07