微重力板式贮箱推进剂重定位的数值仿真

胡 齐，陈 健，李 永

（北京控制工程研究所，北京100190）

微重力板式贮箱推进剂重定位的数值仿真

胡 齐，陈 健，李 永

（北京控制工程研究所，北京100190）

板式表面张力贮箱内推进剂重定位对确定推进剂分布情况、研究晃动影响、提高控制精度等具有重要意义.为研究板式贮箱内推进剂重定位的规律，对微重力下板式贮箱内液体重定位问题进行数值仿真.计算时使用三维非定常两相流动流体（VOF）模型，对某一板式贮箱寿命末期在不同微重力加速度情况下各种重定位过程进行数值仿真，得到各种工况下重定位的全过程，以及定位后推进剂的分布情况.数值仿真结果为板式贮箱的设计提供有利依据.

微重力；板式表面张力贮箱；推进剂；重定位；数值仿真

表面张力贮箱是应用最为广泛的卫星推进剂贮箱，它利用表面张力进行液体输送和气液分离，为发动机或推力器提供不夹气的推进剂［1］.从其推进剂管理装置（PMD，propellantmanagement device）类型来分，表面张力贮箱可以分为筛网式和板式两种.第一代表面张力贮箱都是筛网式的结构，推进剂管理装置使用许多毛细筛网，利用液体在筛网上的表面张力，通过筛网来收集推进剂，同时阻止气体进入管路通道.第二代表面张力贮箱推进剂管理装置则以板式结构为主，尽量减少筛网的使用，利用流体在导流板上的表面张力驱动推进剂，对贮箱内的推进剂实行全管理，可以满足各种流量要求，并适应于不同的微重力环境，尤其是微重力相对较低的大型卫星平台［2］.

板式表面张力贮箱具有结构简单、质量轻、可靠性高等一系列优势［3］.但是板式贮箱的性能不能在地面＋g环境下进行充分验证，对其内部流动规律的验证主要依赖于数值仿真和微重力试验验证［4］.由于微重力试验验证费用昂贵而且需要通过数值仿真提供预估的结果，因此数值仿真在板式贮箱设计中具有极其重要的意义.在板式贮箱的设计中，对微重力环境下贮箱内推进剂重定位的研究至关重要，该研究对确定推进剂分布情况、计算质心位置、研究晃动影响、提高控制精度等都具有重要意义.由于条件所限，以往对推进剂重定位的研究偏重于最终定位结果，随着计算流体力学的发展和计算机性能的提高，求解推进剂重定位全过程成为可能［5－6］.本文使用三维非定常流体的两相流动模型，对某一板式贮箱寿命末期在不同微重力加速度情况下各种重定位过程进行数值仿真，得到各种工况下液体重定位的全过程，以及重新定位后推进剂的分布情况.

1 VOF模型基本原理

VOF模型是一种求解气液两相流动和自由表面流动的算法.最早由美国Los Alamos科学实验室开发用于处理含有自由面的二维粘性流体的数值计算方法［7－8］.该方法通过引入流体体积组分函数及其控制方程来表示混合流体的密度并跟踪自由面的位置.若设α为液相的体积组分，当网格中的体积组分α＝1时，表示该网格内完全是液体，当网格中的体积组分α＝0时，表示网格中完全是气体，当0＜α＜1表示网格中含有气液两相组分.

建立VOF模型时，有两个关键问题需要解决：一个是对气液交界面的重构问题，另一个是交界面随着时间的运移问题.以两相流动为例，当在某一网格内流体体积组分0＜α＜1时，说明这个网格是气液界面，界面重构就是指如何确定界面在网格中的位置.一般来说，VOF模型中界面重构的方法有两类：分段定常界面构造法（PCIC，piecewise constant interface construction）和分段线性界面构造法（PLIC，piecewise linear interface construction）.其中PCIC方法构造精度较低；而PLIC方法是后来发展的，构造精度较高.交界面随时间的运移算法有两种，即算子分裂算法和算子不分裂算法.算子分裂算法将界面从一个时刻到另一个时刻的运移过程看作界面分别在不同方向运动的合成；算子不分裂算法是直接根据网格中流体的当前位置和速度，判断下一个时刻流体到达的位置，直接得到下一个时刻各个网格内的流体分布.

（1）物性方程

流体的物性是由流体中不同相的体积组分确定的，物性方程就是不同体积组分流体物性的表达式.贮箱内部流动只有气液两相，假设第二相的体积组分被跟踪，那么流体的密度属性方程为：

式中，ρ为混合流体的密度，α1、α2分别为第一相和第二相的体积组分；ρ1、ρ2分别为第一相和第二相的密度，它们为给定值.

（2）连续方程

流体连续方程的基本表达式如下：

式中，u为混合流体速度，R为源项.

刘雁衡睁开眼，说了一句令石警官很不满的话。刘雁衡把冻僵的左手手指蜷起来，和右手一起把箫抱到胸前，淡淡对四小姐说：“对不起，你挡了我的风。”

根据物性方程（1）和连续方程（2）可以得到各相体积分数的运移方程：

式中，αq为第q相的体积组分，R是由净相变引起的，R＝Re－Rc，其中Re表示蒸气生成率，Rc表示蒸气凝结率.在本模型中，由于R很小，故在求解时将此项可忽略不计.

（3）动量方程

混合流体的动量方程为：

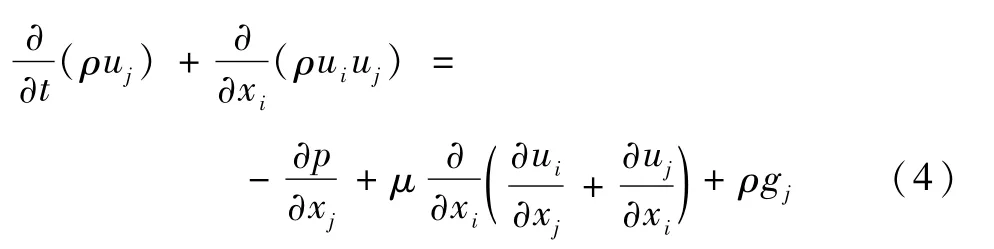
式中，p为贮箱压力，uj，ui分别为二相混合流的液相和气相速度，xj，xi分别为二相混合流的液相和气相位置，t为时间，gj为微重力加速度，μ为粘性系数.由于表面张力的作用，在界面处有：

式中，σ为表面张力系数，r为液带曲率半径，联立式（4）和式（5），得：

这就是混合流体的动量方程.

2 计算模型

计算选用如图1所示的贮箱结构，液体位于贮箱下半球蓄液器区域.采用结构化网格对蓄液器区域进行网格划分，如图2和图3所示.整个蓄液器内计算区域网格数为203 866，整个蓄液器与贮箱计算区域网格数为178 368.

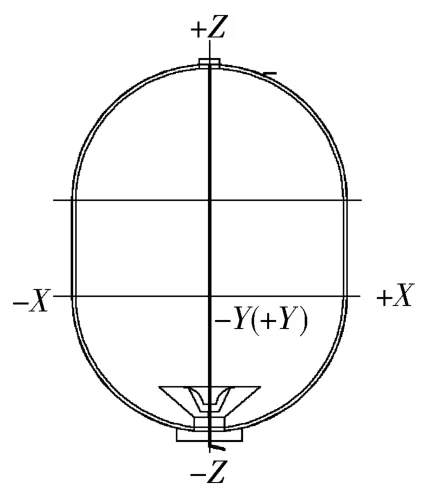
图1 贮箱结构图

计算时，采用液态酒精作为模拟介质，表面张力系数为0.022 03 N／m.假设整个蓄液器内以及蓄液器与贮箱壁区域是处于密封状态，将各个壁面都设为固壁边界条件，即采用无穿透、无滑移边界条件.

在初始情况下，假设模拟推进剂处于沉底状态.计算域包括液体和气体两部分，在进行计算时，先设定计算域内的初始体积组分分布作为计算域内气液两相分布的初始条件.初始化时设定液面高度，在该区域内模拟推进剂的体积组分为1；其余区域模拟推进剂的体积组分为0.

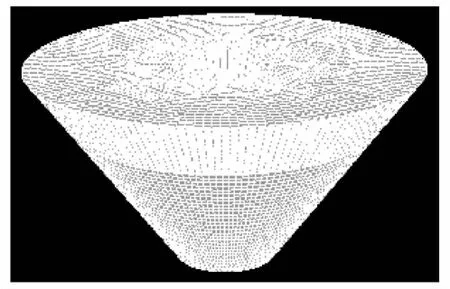
图2 蓄液器网格图

图3 蓄液器与贮箱壁区域网格图

3 计算结果及分析

在寿命末期贮箱内推进剂应该定位在蓄液器区域即贮箱出液口处，从而贮箱可以长时间为推力器提供不夹气的推进剂.根据卫星在轨工作情况，考虑零重力、10－3g微重力（－X、－Y方向），10－4g（－X方向）等微重力环境.

本文采用VOF两相流动模型，模拟各种微重力情况下蓄液器内和蓄液器与贮箱壁区域内的推进剂的重定位过程，具体结果如下.

3.1 蓄液器内推进剂重定位过程

（1）各种微重力加速度下液面的分布

图4描述在各种微重力加速度下蓄液器内重定位过程中液面的最终分布状态，图中深色部分代表模拟介质.

（2）零重力情况下重定位过程

在零重力情况下，推进剂将从沉底状态沿着蓄液器弧壁向上缓慢爬升，并能够到达蓄液器顶部.由于蓄液器顶部与蓄液器弧壁夹角较小，在表面张力的作用下有利于推进剂的蓄留，之后推进剂继续沿着顶部先前缓慢爬升，但是由于顶部是平面而不是弧面，表面张力不足以支撑推进剂继续先前爬升，最终重定位的状态如图4（a）所示.

（3）10－3g微重力（－Y方向）情况下重定位过程

在10－3g微重力（－Y方向）情况下，推进剂重定位过程存在振荡的现象，推进剂在表面张力的作用下沿着蓄液器壁面向上爬升，在达到一定高度之后向下跌落，然后又沿着壁面向上爬升，如此振荡多次，逐渐达到平衡状态，形成如图4（b）所示的凹面.推进剂重定位过程所引起的振荡会造成整个贮箱质心移动，这对卫星的控制精度会产生一定影响，因此对整个振荡过程的准确模拟能够为提高卫星控制精度提供有利参考价值.

（4）10－3g微重力（－X方向）情况下重定位过程

在10－3g微重力（－X方向）情况下，在微重力和表面张力作用下，推进剂从沉底状态向－X方向运动，迅速充满－X方向的半个蓄液器，并将其顶部淹没，若此时顶部没有密封，推进剂将从该位置进入蓄液器外部.然后液面形状也开始振荡，并最终趋于平衡，达到图4（c）所示的状态.

图4 不同微重力下蓄液器内液面最终分布

3.2 蓄液器与贮箱壁区域内推进剂重定位过程

（1）各种微重力加速度下液面的分布

图5描述各种微重力加速度下蓄液器与贮箱壁区域重定位过程中液面的最终分布状态，图中深色部分代表模拟介质.

图5 不同微重力下蓄液器与贮箱区域液面最终分布

（2）零重力情况下重定位过程

在零重力情况下推进剂在表面张力作用下将从沉底状态沿着贮箱壁和蓄液器外壁弧面向上缓慢爬升，期间出现液面不断的振荡，直到表面张力不足以支撑推进剂继续向上爬升，逐渐形成较规则的液面，最终重定位的状态如图5（a）所示.

（3）10－3g微重力（－Y方向）情况下重定位过程

在10－3g微重力（－Y方向）情况下，推进剂重定位过程仍然存在振荡的现象，开始阶段，推进剂在表面张力的作用下沿着贮箱壁面和蓄液器壁面向上爬升，在达到一定高度之后向下跌落，然后又沿着壁面向上爬升，如此振荡多次，逐渐达到平衡状态形成较规则液面，最终重定位状态如图5（b）所示.

（4）10－4g微重力（－X方向）情况下重定位过程

在10－4g微重力（－X方向）情况下，开始阶段，由于微重力相对表面张力较小，推进剂在表面张力的作用下仍然沿着贮箱壁面和蓄液器壁面向上爬升，期间液面也仍然存在振荡的现象，在达到一定高度之后，在微重力作用下，推进剂缓慢地向－X方向运动，液面同时存在振荡，但由于微重力的值较小，振荡幅度大幅减小，最终趋于平衡，达到图5（c）所示的状态.

4 结 论

（1）通过数值仿真得到不同工况下推进剂重定位的全过程以及定位后推进剂的分布情况，结果表明这种板式PMD可以有效地蓄留推进剂，为推力器提供不夹气的推进剂，验证其对推进剂管理的良好性能.

（2）对不同工况下推进剂重定位过程的研究，可以为整个贮箱在卫星不同工作状态下推进剂的分布提供参考，进而为板式贮箱的设计提供有利依据.

（3）推进剂重定位过程是个动态过程，存在反复振荡现象.对推进剂重定位的过程数值仿真得到推进剂液面振荡的全过程，进而为提高卫星控制精度提供有益的参考.

［1］ Rollins JR，Grove R K，Jaekle Jr D E.Twenty－three years of surface tension propellant management system design，development，manufacture，test，and operation［R］.AIAA 85－1199

［2］ 李永，潘海林，魏延明.第二代表面张力贮箱的研究与应用进展［J］.宇航学报，2007，28（2）：503－507

［3］ Debreceni M J.W illiam D L，Jaekle Jr D E，Graffer A C.Design and development of the AXAF－IPS PMD＆PMD integration［R］.AIAA 97－2812

［4］ Netter G，Renner U，Dreyer M.Design and verification of a standard surface tension propellant tank［C］.The 35thJoint Propulsion Conference and Exhibit，Los Angeles，California，June 20－24，1999

［5］ 潘海林，洪儒珍.挡板对液体推进剂晃动力的影响［J］.中国空间科学技术，2000（1）：6－12

［6］ 潘海林，魏延明，洪儒珍.微重力环境中重力梯度加速度引起的流体晃动力和力矩的模拟［J］.宇航学报，1998，19（2）：66－72

［7］ Torrey M D，Cloutman L D，M jolsness R C.NASAVOF2D：a computer program for incompressible flows with free surfaces［M］.Los Alamos National Lab，LA－10612－MS，1985

［8］ Hirt CW，Nichols B D.Volume of fluid（VOF）method for the dynamics of free boundaries［J］.Journal of Computational Physics，1981（39）：201－225

Numerical Simulation for Reorientation of Propellant in a Vane Tank under Microgravity

HU Qi，CHEN Jian，LIYong
（Beijing Institute of Control Engineering，Beijing 100190，China）

Reorientation of propellant in a vane surface tension tank is of great significance for the ascertainment of propellant distribution，and research on liquid shaking mechanism，and improvement of control accuracy and so on.In order to investigate a law of propellant reorientation，propellant reorientation processes in vane type tank under different microgravity conditions are numerically simulated.The paper introduces a twophase flow model of three-dimensional unsteady VOF（volume of fluid），and based on the model numerical-ly simulates all kinds of reorientation processes in a vane type tank during near depletion phase under different microgravity acceleration conditions，then all processes of propellant reorientation under different working conditions and propellant distributions after reorientation are obtained.The simulation results provide advantageous foundation for design of the vane tank.

microgravity；vane surface tension tank；propellant；reorientation；numerical simulation

V43

A

1674-1579（2009）06-0054-04

2009-09-22

胡 齐（1985—），男，江西人，硕士研究生，研究方向为航天推进技术（e-mail：hqbuaa03＠sohu.com）.