基于单目视觉的非合作航天器相对位置和姿态测量算法

张劲锋，孙承启，蔡 伟

（1.北京控制工程研究所，北京100190；2.空间智能控制技术国家级重点实验室，北京100190）

基于单目视觉的非合作航天器相对位置和姿态测量算法

张劲锋1，2，孙承启1，2，蔡 伟1

（1.北京控制工程研究所，北京100190；2.空间智能控制技术国家级重点实验室，北京100190）

对非合作航天器的相对位置和姿态测量问题进行了研究，提出了一种新的单目视觉测量算法——相似迭代算法.该算法根据相似三角形原理推导出一种新的深度迭代机制，通过深度估计和绝对方位问题求解两个步骤对相对位置和姿态参数进行迭代计算.数值仿真结果表明了该算法的有效性.

单目视觉；非合作航天器；相对位置和姿态

在空间交会对接、在轨服务等航天任务的最后逼近段，通常采用光学成像敏感器来测量追踪航天器与目标航天器之间的相对位置和姿态（以下简称相对位姿），国内外许多学者已经对合作目标航天器（目标航天器上安装有目标标识器）的视觉测量算法进行了大量研究［1-3］.针对合作目标的相对位姿测量方法虽有精度高、抗干扰能力强的特点，但其作用距离受限于合作目标尺寸，且只能对装有目标标识器的航天器进行测量.而针对非合作目标的相对位姿测量方法，不仅可对合作目标测量方法形成冗余，而且可对没有安装目标标识器的非合作或敌对目标（统称为非合作目标）航天器的相对位姿进行测量.该方法本身具有重要的实际应用价值和潜在的军事用途，已经引起了国内外许多学者的关注［4-5］.

本文从非合作目标测量的实际需求出发，对非合作航天器相对位姿测量问题进行了研究，提出了一种新的单目视觉测量算法.由于该算法的主要特点是根据三角形相似原理提出一种新的深度迭代机制，因此本文称之为相似迭代算法.该算法的每一个步骤均有多种实现方法，本文利用直接线性变换算法［6］来求解深度初值，利用单位四元数求解绝对方位问题［7］.

1 问题描述

假设摄像机已经过标定，如图1所示，目标坐标系为OoXoYoZo，摄像机坐标系为OcXcYcZc，焦距为f，z轴垂直于图像平面G.平面H通过目标坐标系原点Oo且平行于图像平面G，H与摄像机坐标系原点Oc的距离为zc0，即点Oo在摄像机坐标系中的z轴坐标.目标上点Pi在平面H上的正交投影点为Mi，Mi在图像平面上的透视投影为点mi，即点Pi的弱透视投影点为mi，其透视投影为点pi.分别从点Pi、Mi和pi向轴OcZc作垂线，垂足分别为点E、D和C.

现给定三维目标上的一组特征点Pi，i＝1，2，…，n，n≥6均位于摄像机的视场内，令特征点Pi在目标坐标系中的坐标poi＝［xoi，yoi，zoi］T，在摄像机坐标系中的坐标为pci＝［xci，yci，zci］T，则

其中，

图1 相关坐标系和摄像机成像模型

展开式（1），可得

在摄像机坐标系中，点Pi经过透视变换，得到对应的2维投影图像点pi，令点pi在图像坐标系中的坐标为［ui，vi］T，则

将式（3）代入式（4），可得

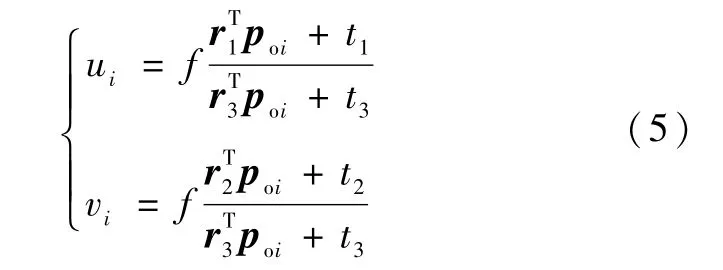
要解决的问题就是在已知目标特征点坐标及其对应的图像坐标的条件下，根据式（5）所表达的非线性约束，求解未知的姿态旋转矩阵R和平移向量t.

2 相似迭代算法

本文提出的相似迭代算法包括深度估计和绝对方位问题求解两个步骤.在深度估计步骤，利用新的深度迭代公式估计新的深度值；在绝对方位问题求解步骤，由上一步得到的深度值构造所谓的绝对方位问题，求解出相对位姿参数.对上述两个步骤进行反复迭代，直至满足一定的收敛条件.对于迭代初值可以用多种算法来求解，由于直接线性变换算法［6］较为简单，速度快，因此本文采用该算法用于求解迭代初值.

2.1 深度估计

由图1所示，在摄像机坐标系中，令di表示向量的长度，这里称为点Pi的深度值.在ΔOcEPi中，由于Cpi∥EPi，根据三角形的相似性，有

又已知

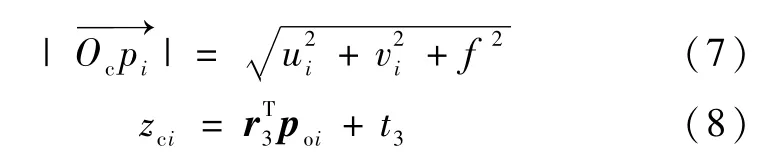
可得

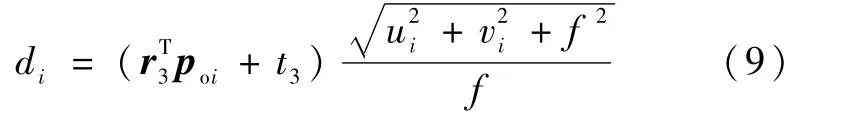
显然，若已计算出r3和t3，则可利用上式迭代计算各个特征点的深度值di.

2.2 绝对方位问题求解

令si表示向量方向上的单位向量，即

则点Pi在摄像机坐标系中的坐标为

现在已知目标特征点Pi在目标坐标系中的坐标poi及其在摄像机坐标系中的坐标pci，要求解目标坐标系与摄像机坐标系之间的刚体变换，即旋转矩阵R与平移向量t，该问题常称之为绝对方位问题［7］.

求解绝对方位问题有多种算法，文献［7］利用单位四元数表达旋转矩阵，给出了问题的闭式解，本文采用该算法来求解绝对方位问题.

1）计算两个三维点集的均值，将数据归一化

2）构造反对称矩阵

式中（·）×表示向量对应的叉乘矩阵.

3）对矩阵A进行特征值分解，则矩阵A的最小特征值对应的特征向量即为所求的单位四元数q.将单位四元数q转化为旋转矩阵R，则所求的平移向量为

2.3 求解深度初值

本文利用直接线性变换算法［6］来求解初始的相对位姿参数R和t，然后由式（9）计算深度的初始值.

将相对位姿参数R和t组合成一个12维向量h，即

则式（5）可改写为如下线性方程组：

式中2n×12系数矩阵A为

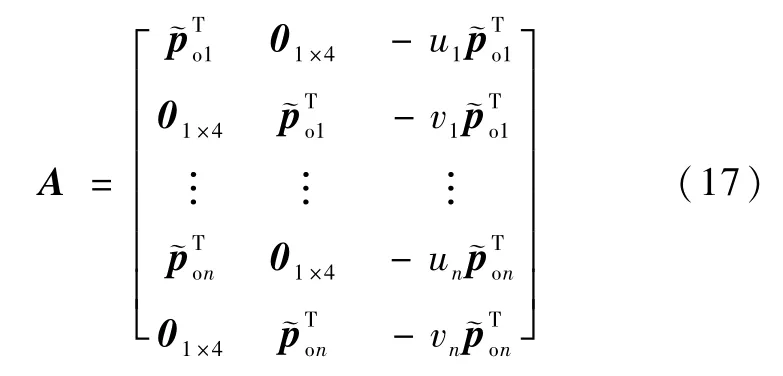
直接线性变换算法就是求解合适的h，使得‖Ah‖为最小，一般约束条件取‖h‖＝1，利用拉格朗日乘子法，可得下面的无约束优化目标函数

对上式求h的偏导数，并令其为0，可得

可得

可知，所求的向量h是对应于对称矩阵ATA的最小特征值λ的特征向量.

利用上述算法求得旋转矩阵R和平移向量t后，就可由式（9）对深度值进行迭代更新.如果前后两次迭代的深度误差小于某个阈值，则停止迭代，并输出相对位姿参数R和t；否则继续进行迭代循环.

3 数值仿真

为了验证本文提出的相似迭代算法的有效性，利用Matlab软件进行了数值仿真.

为了简化计算，取非合作航天器的本体为1×1×1的立方体，航天器带两个太阳帆板，如图2所示.

图2 仿真用的目标航天器模型

将航天器的18个顶点作为目标特征点，各特征点在目标坐标系中的坐标如表1所示，这里不考虑遮挡问题.

表1 特征点在目标航天器坐标系中的坐标

固定平移分量t1＝5，t2＝5，以t3为变量，取步长为1，在5～500内变化；在每个距离点处，3个旋转角θ1、θ2和θ3按照均匀分布在－30°～30°间随机取值，并产生1 000个旋转矩阵.由得到的旋转矩阵和平移向量分别对特征点进行刚体变换和透视投影变换，得到对应的图像特征点.假设图像噪声的方差σ与信噪比τ的关系为

取信噪比为80 dB，由式（21）算出不同距离处的图像噪声方差σ，在图像点坐标中加入均值为0、方差为σ的高斯随机噪声.利用本文提出的相似迭代算法计算出3个旋转角和3个平移分量在不同距离处的平均误差，仿真结果如图3和图4所示.

图3 相对姿态误差随目标距离的变化

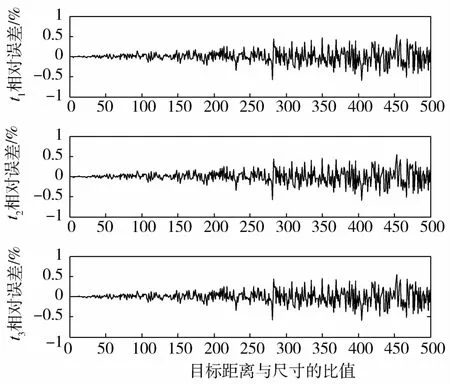
图4 相对位置误差随目标距离的变化

由图3和图4可知，相对位姿的平均误差均随着目标距离的增大而增大，3个旋转角的最大平均误差不超过0.5°，平移分量的最大相对误差不超过1%，能够基本满足非合作航天器相对位姿参数的测量要求.如果星载计算机运算能力和时间允许，还可以采用更为精确的迭代初值或适当增加迭代次数来获得更高的测量精度.

4 结 论

本文对非合作航天器的相对位姿测量问题进行了研究，提出了一种新的单目视觉测量算法——相似迭代算法.数值仿真结果表明该算法具有精度高、抗噪声能力强的优点，能够基本满足非合作航天器相对位姿测量的需求.此外，该算法还提供了一种灵活的分步实现框架，其中的每个步骤可分别用多种方法来实现，有利于算法的进一步改进和推广.

［1］ Ho C C，Mc-Clamroch N H.Aspacecraft docking problem：position estimation using a computer vision approach［C］.AIAA Guidance，Navigation and Control Conference，Portland，USA，Aug 1990

［2］ Calhoun P C，Dabney R.Solution to the problem of determining the relative 6 DOF state for spacecraft automated rendezvous and docking［J］.SPIE，1995，2466：175-184

［3］ 林来兴，李灿.交会对接逼近阶段CCD相机的测量方法［J］.宇航学报，1994，15（2）：24-34

［4］ Cropp A，Palmer P L，Mc-Lauchlan P，et al.Estimating the pose of a known target satellite［J］.IEE Electronic Letters，2000，36（15）：1331-1332

［5］ 张世杰，曹喜滨，陈闽.非合作航天器间相对位姿的单目视觉确定算法［J］.南京理工大学学报，2006，30（5）：564-568

［6］ Hartley R，Zisserman A.Multiple view geometry in computer vision［M］.Cambridge：Cambridge University Press，2003

［7］ Horn B K.Closed-form solution of absolute orientation using unit quaternion［J］.Journal of the Optical Society of America，1987，4（4）：629-642

Monocular Vision-Based Relative Position and Attitude Measurement Algorithm for Non-Cooperative Spacecrafts

ZHANG Jinfeng1，2，SUN Chengqi1，2，CAIWei1
（1.Beijing Institute of Control Engineering，Beijing 100190，China；2.National Key Laboratory of Science and Technology on Space Intelligent Control，Beijing 100190，China）

Anovel monocular vision-based relative position and attitudemeasurement algorithm named as the Sim ilar Iteration algorithm is presented for non-cooperative spacecrafts in this paper.The algorithm derives a new depth iteration mechanism from principle of triangular similitude and involves two steps，i.e.the depth estimation and solving the absolute orientation problem.Numerical simulations have demonstrated the effectiveness of the proposed algorithm.

monocular vision；non-cooperative spacecraft；relative position and attitude

V448.2

A

1674-1579（2009）06-0050-04

2009-02-25

张劲锋（1979—），男，河南人，博士研究生，研究方向为空间目标识别与相对测量（e-mail：zjf519＠yahoo.com.cn）.