基于太阳敏感器的静止轨道卫星轨道估计方法研究

徐菁宇，高益军

（北京控制工程研究所，北京100190）

基于太阳敏感器的静止轨道卫星轨道估计方法研究

徐菁宇，高益军

（北京控制工程研究所，北京100190）

为解决目前通过星上配置敏感器进行地球同步轨道卫星自主轨道估计的问题，利用太阳敏感器和红外地球敏感器的测量信息进行轨道估计.根据地球静止轨道的特点，结合Hill方程，利用太阳敏感器和红外地球敏感器的测量信息以及轨道的摄动特性，建立导航系统的状态方程和测量方程.数学仿真结果表明，该方法可以较准确地估计出卫星的经度漂移，是一种可行的地球同步轨道卫星自主导航方法.

静止轨道卫星；太阳敏感器；红外地球敏感器；轨道估计

随着地球静止轨道卫星的发展，对其自主生存能力的要求越来越高.卫星实现自主生存的一个重要因素是卫星轨道的自主估计和自主控制.高轨道天文导航方法基本上采用的是星敏感器和红外地球敏感器相结合的自主轨道确定方法，这种方法的优点是经度和纬度偏差均可进行估计，但是由于星敏感器的使用复杂性及星敏感器的费用相对较高等因素导致了这种方法不能广泛使用［1］.一般文献中给出的导航方法在测量数据比较完备的情况下能有效给出轨道六要素.极少情况下也有考虑测量受限时通过各种预报、估计等方法给出轨道要素的情况，如在文献［2］中，提出了利用太阳敏感器和星敏感器进行轨道确定，该文献着重考虑了滤波算法的稳定性，但没有对系统能观性等问题进行详细阐述.本文正是在此种测量受限的情况下，根据星上现有的太阳敏感器和红外地球敏感器的测量信息进行轨道估计，该系统显然是不能观的，但可以通过系统降维处理等近似方法，滤波得到卫星东西漂移量，而不去深究各个轨道要素的变化.本系统对于卫星南北漂移量可通过外推估计得到，对于东西漂移量测量精度在30天内可达到±0.02°，这一结果在工程上具有较大的实用价值.

1 摄动对静止轨道的影响

对于静止轨道卫星而言，影响卫星轨道的摄动因素有很多，主要有地球非球形摄动、日月引力摄动、太阳光压摄动.在文献［2-3］中阐述了这些摄动因素对地球静止轨道卫星的影响.其他摄动，如大气阻力摄动、后牛顿效应摄动、坐标系附加摄动等，摄动力的数量级与上面三种摄动相差甚远，所以本文在研究静止轨道卫星受摄动力影响时，只考虑上面三种主要摄动因素.图1～3给出了轨道半长轴、轨道倾角和偏心率在摄动作用下的长期变化规律.图1为定点位置在东经120°的卫星的半长轴在30多天中的变化曲线.图2为两颗卫星的倾角矢量在一年内不受控制时的变化，其中，ix为倾角矢量在x轴方向的分量，iy为倾角矢量在y轴方向的矢量.图3为偏心率在一年内的变化，其中，ex为偏心率矢量在x轴方向的分量，ey为偏心率矢量在y轴方向的分量.

通过摄动分析可知：摄动干扰对轨道要素的影响具有一定的规律性，特别是偏心率矢量和倾角矢量在摄动干扰下具有很强的变化趋势.当卫星位置估计精度要求不是很高时，卫星的南北位置可以按倾角矢量进行估计，偏心率矢量和倾角矢量均可以用较简单的数学方法进行描述.但是，东西方向受各种摄动影响较大［4］，长时间外推必然偏离真实值，所以一般地面需要定期进行星上轨道要素的更新，以维持一定的导航精度，显然频繁的数据注入不利于卫星的自主生存，同时也给地面长期在轨管理增加了负担，因此，本文寻求一种简便的算法估计东西方向上的变化趋势.

图1 半长轴变化规律

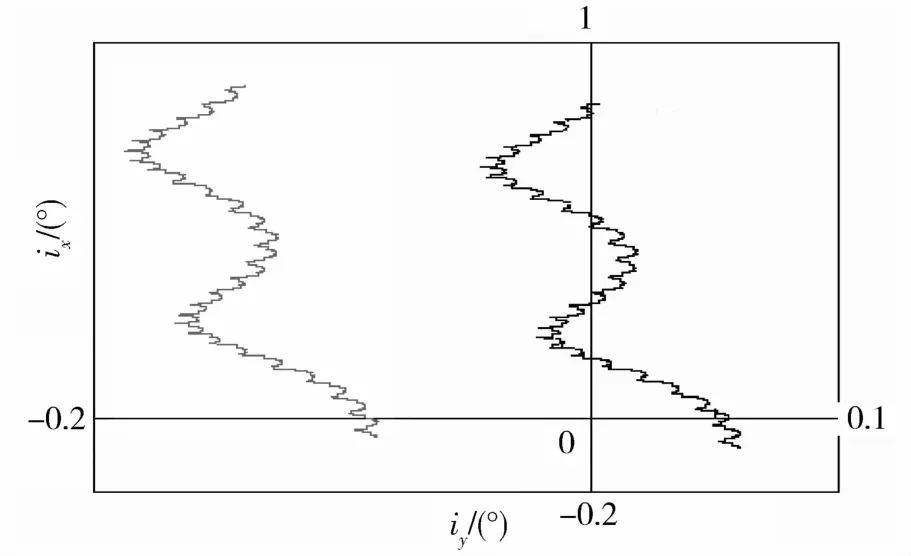
图2 倾角矢量在一年内的变化特性

图3 偏心率在一年内的变化特性

2 轨道估计方法研究

2.1 系统状态方程的建立

假定静止轨道上有一颗假想卫星在运动，它不受摄动影响，则卫星每一天环绕地球一圈，相对地面方位固定，在其上建立标称静止轨道坐标系.而对于在静止轨道上运动的受摄动影响的卫星，通常要求卫星在东西方向的偏差不超过±0.1°，南北方向的偏差不超过±0.1°.如图4所示，其中方块代表真实卫星，在小方块下面的小椭圆代表假想卫星［1］.

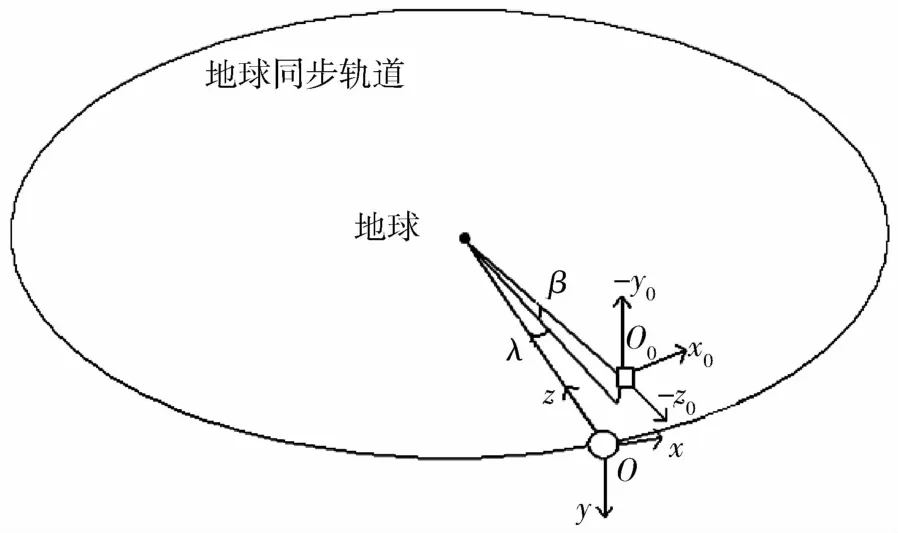
图4 静止轨道坐标系下假想卫星与真实卫星的运动情况

在标称静止轨道坐标系下，真实卫星相对于假想卫星的相对运动方程——Hill方程为

式中，ω0是静止轨道的轨道角速度，ax、ay、az是作用在卫星上的摄动加速度在标称静止轨道坐标系上的分量.将经度漂移λ＝x／rgeo，纬度漂移β＝y／rgeo，径向漂移r＝z／rgeo代入到式（1）中

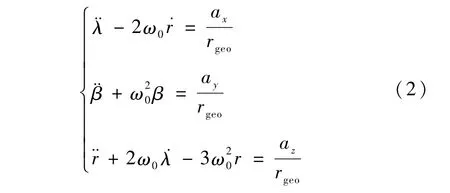
式中，rgeo是静止轨道的半径，λ和β的空间表示见图4.

定义状态矢量X

由于卫星在南北方向上的运动较有规律，可以在相对较长的一段时间内外推获得卫星的南北漂移量β，因此测量数据主要估计东西方向上的漂移λ.通过调整X的排列，得到两个向量X1和X2

状态方程可写为

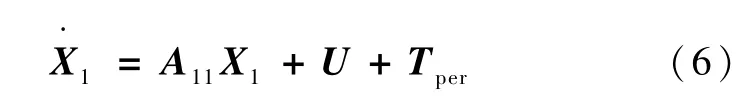
根据方程（2）可知

设当0≤t0≤T（30天）时，对方程（7）的两边进行积分，可得

将式（8）代入到方程（2）的第1个方程中

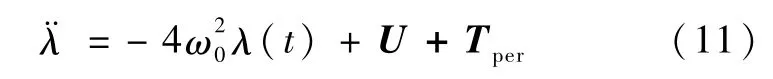
则系统（6）中

2.2 系统测量方程的建立

根据太阳敏感器和红外地球敏感器的测量信息得到太阳相对于卫星的单位矢量S1，地心相对于卫星的单位矢量E.S2是太阳相对于标称静止轨道坐标系原点O的单位矢量，Z是地心相对于标称静止轨道坐标系原点O的单位矢量.空间方位见图5，A代表太阳敏感器，B代表红外红外地球敏感器.因此可得到两个夹角η、η′

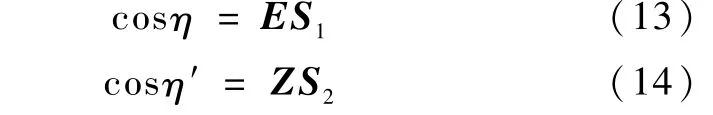
由此得到测量矢量g

θ为假想卫星所在处的赤经，则E、S1、S2、Z在地心赤道惯性坐标系中的坐标［1］

式中，Γ为测量误差，根据式（20），同时认为卫星在南北方向上的偏移β是小量，即cosβ≈1，则可建立导航系统的观测矩阵C1，其线性化后的表达式为

图5 空间方位图

2.3 能观性说明

状态方程及测量方程如下：

由此能够建立起轨道估计系统的能观性矩阵

当S2xsinθ－S2ycosθ≠0时，判断线性时变系统的能观性，计算得到矩阵的秩为2，所以式（22）所示的子系统是能观的.事实上，若子系统能观性矩阵的秩为2，则要求S2xsinθ－S2ycosθ≠0，当｜S2xsinθ－S2ycosθ｜＜δ（0＜δ≪1）时，系统的能观性很差.因此，使用此测量方程时，要避免使用S2xsinθ－S2ycosθ在0附近的数据，即当太阳、地球、卫星处在一条直线附近时，不要进行经度漂移估计.

2.4 数学仿真

仿真条件为：起始时间2010年3月24日08时00分00秒；仿真初始轨道要素a＝4.216 5×107m，e＝0.000 4，i＝0.01°，Ω＝220°，ω＝100.1°，f＝80°；仿真采样周期为1 min；红外地球敏感器测量噪声0.03°(3σ)；太阳敏感器的视场范围为－60°～60°；当视场范围为－25°～25°时，太阳敏感器的测量噪声是0.05°（3σ），否则为0.1°（3σ）.

在卫星稳定运行期间，图6显示太阳敏感器与红外地球敏感器在没有测量噪声的前提下3天内的经度漂移仿真曲线.由于太阳敏感器使用的特殊性，因此在太阳可见的情况下给出测量值.图中矩形波反映了太阳可见和太阳不可见的情况，当矩形波为0.1时太阳可见，当矩形波中较短一段为0时也是太阳可见的情况.但是在Kalman滤波时，当测量方程矩阵中出现接近0的较小值时，滤波增益矩阵出现计算奇异，对应的系统能观性急剧下降，表现为太阳敏感器的测量范围在20°之内滤波结果误差明显增大.因此仿真中取太阳敏感器测量信息在20°之外的测量值.矩形波中较长一段为0时太阳不可见，此时滤波后数据保持不变.

图6 3天内经度漂移真实值与导航值的仿真曲线

在实际应用该方法时，会碰到一个非常重要、也非常可能出现的问题，就是Kalman滤波的初始值不够精确的问题.在此仅给出状态变量λ在初始值估计偏差较大的情况下的仿真曲线，见图7.从图中可以看出，无论初始值估计偏差有多大，系统都能很好地跟踪卫星在东西方向上的变化，得出卫星在空间的运动趋势.

从30天的仿真曲线上可以看出，经过几个小时的滤波后，选取最后的滤波值作为导航值，导航值与真实值的误差在0.02°范围内，说明系统能够很好地跟踪东西方向上的变化（如图8所示）.图中仿真用的30天测量数据中无系统误差，但包含测量噪声.真实星上敏感器测量时存在系统误差，此系统误差一般为恒定量，可以通过地面测轨标定获得，并且可以通过在轨进行补偿，因此系统误差在东西方向上的轨道估计可以得到修正.

图7 初始偏差较大时经度漂移导航值与估计值的仿真曲线

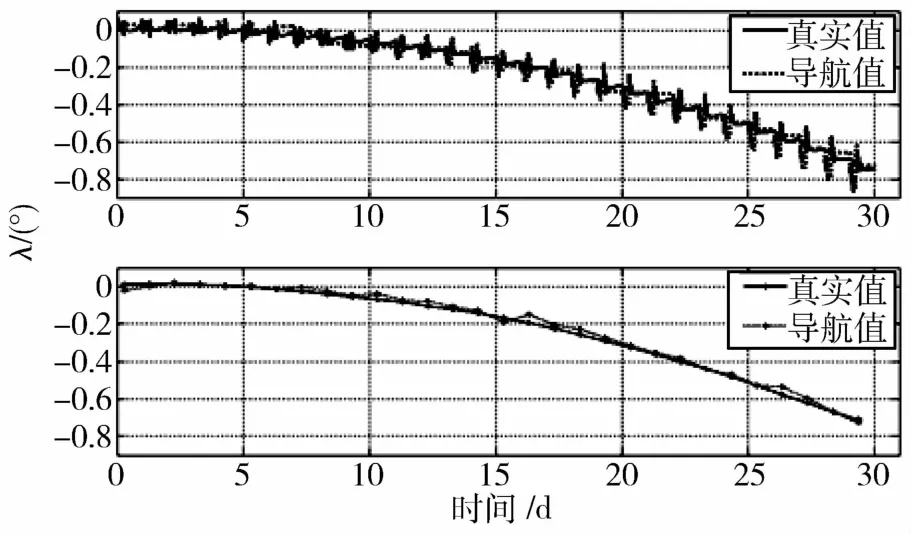
图8 30天精度漂移真实值与导航值仿真曲线

3 结束语

本文结合地球静止轨道的特点，用太阳敏感器和红外地球敏感器的测量信息进行静止轨道卫星的轨道估计，其特点是：导航系统采用星上常用的基本配置姿态敏感器——太阳敏感器和红外地球敏感器，导航算法简单，实现成本低，且在较长时间内，可以估计出东西漂移量以及外推得到的南北方向轨道参数，从而较准确地得到了卫星的位置，基本满足了星上轨道估计的需要.

［1］ 郭建新，解永春.基于姿态敏感器的地球同步轨道卫星自主导航研究［J］.航天控制，2003，21（4）：1－6

［2］ 任之幸.使用姿态敏感器的自主卫星导航和轨道保持［J］.宇航学报，1986，7（1）：22－31

［3］ Eric Ms.地球静止轨道手册［M］.北京：国防工业出版社，1999

［4］ Gottzein E.Challenges in control and autonomy of communications satellites［C］.IFAC Automatic Control in Aerospace，Seoul，Korea，1998

［5］ 章仁为.卫星轨道姿态动力学与控制［M］.北京：北京航空航天大学出版社，1998

Sun Sensor-Based Orbit Position Estimating Method for GEO Satellites

XU Jingyu，GAO Yijun
（Beijing Institute of Control Engineering，Beijing 100190，China）

In order to estimate orbit position of GEO satellites using existing on-board equipments，this paper describes the system composed of sun sensors and earth sensors.According to nature of orbit of GEO satellites combined with Hill equation，state equations and measurement equations of this system are established by using measurement information from sun sensors and earth sensors，as well as orbit perturbation characteristics.Simulation results show that longitude’s excursion of the satellite can be accurately estimated by this method，and it is a feasible autonomous navigation method for GEO satellites.

GEO satellite；sun sensor；earth sensor；orbit’s estimation

V249.32

A

1674-1579（2009）06-0041-04

2009-06-22

徐菁宇（1977—），女，北京人，工程师，研究方向为卫星自主导航（e-mail：xujingy＠sina.com）.