素质化数学课堂教学应如何建构

耿占平

摘 要:数学课堂教学要素质化,其核心就是在数学课堂教学过程中,加强知识发生过程的教学,充分调动学生思维的主动性、积极性,有计划、有目的地培养学生的思维能力和创造能力,有效地渗透数学思想,让学生主动建构有个性色彩的数学思想体系,引导学生更好地重建认知结构,以形成带有个性特征的数学观念,从而达到提高学生整体数学素养的目的。

关键词:数学教学;素质化建构;数学能力;估算能力;数学观念;数学思想方法

中图分类号:G633.6 文献标识码:A 文章编号:1009-010X(2009)06-0047-02

数学课堂教学要素质化,其核心就是在数学课堂教学过程中,加强知识发生过程的教学,充分调动学生思维的主动性、积极性,有计划、有目的地培养学生的思维能力和创造能力,有效地渗透数学思想,让学生主动建构有个性色彩的数学思想体系,引导学生更好地重建认知结构,以形成带有个性特征的数学观念,从而达到提高学生整体数学素养的目的。作为构成学生数学素质的四大要素:数学能力、估算能力、数学观念、数学思想方法,如何去建构它们将是实施数学课堂教学素质化的关键问题。

一、数学能力的建构

所谓能力,说法很多。一般认为,能力是符合活动要求,影响流动效果的个性心理特征,而数学能力应具备数学特点,一般指“运算能力、逻辑思维能力和空间想象能力”,严格说,还应包括创造力,这也是21世纪对人才的需要标志之一。由此可见,数学能力是学生通过思考,采用比较、分析、综合概括、联想,把原认知结构中的知识技能进行组合再组合,从而主动构建起新的认知结构的本领。因此,在数学课堂教学中,应使“课堂”成为学生进行有意义活动的“学堂”,课堂内提倡的是一种“鼓励独立思考、合作学习、大胆猜测、合理推断、主动交流和相互尊重理解”的氛围,应当创造一种“有利于促进学生的数学能力充分发展的教学环境”。

二、估算能力的建构

估算是一种开放型的创造性活动,往往带有很多不确定因素,有时结果也不是唯一的。这就要求学生知道什么时候估算是可行的,如何提取主要因素,哪些数据可忽略不计。这些技能的培养不是一朝一夕所能造就,而要贯穿于数学教学的全过程。数学估算的方法很多,像由特殊估算一般、由局部估算整体、由一般规律估算个体情况等,现在广泛使用的特例法,其实就是一种简单的估算。比如,一袋方便面有多重?告诉你有50克、125克、500克、600克四个答案,那么你选择哪一个?这时只需心算或简单估计即可。

三、数学观念的建构

数学观念并不是外界和别人强加的,而是以知识为载体、经验为中介,经过主体的建构才得以形成。比如:a°=1,为什么规定a°=1?规定a°=2行吗?这些“规定”对于初学者来说很抽象,但随着知识的掌握与积累,不断反思,这些“规定”的观念得以建构发展,便可认识到这些“规定”的合理性、必要性。

四、数学思想的建构

在课堂数学中,如何有效地发展学生的数学思想呢?首先,我们可以把诸如转化思想、数形结合的思想、由特殊到一般再由一般到特殊的思想、整体的思想、比较的思想等等数学思想先传授给学生,这时,学生接受的思想框架可能空洞,可能未被理解;其次,再让学生自己的思维活动逐步理解它并内化为认知形态的数学思想,构建起较为系统的、独立的、活化的数学思想体系。例如“梯形中位线定理”的教学,可作如下设计:

1.创设问题情境。问题1:如图1,直线AB∥EF∥DC,当AE=ED时,则BF与FC有何关系?线段EF可看作梯形ABCD的什么线。

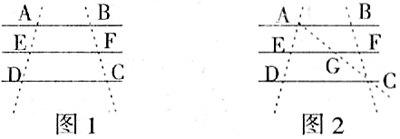
问题2:三角形的中位线有何性质?你能猜想一下梯形的中位线EF具有什么性质吗?

2.学生自主探索与研究。根据实际情况,决定教师的介入程度,教师可构建解决问题的框架,鼓励学生自主探索研究。

①在图2中,连结AC交EF于G点,则AC与GC在数量上有何关系?

②从位置上观察EF具什么性质?

③测量一下EF,在数量上又具有什么性质?

3.构建数学思想。如何验证猜想EF∥AB,EF=1/2(AB+CD)呢?

方案一 ①转化为三角形中位线,如何实现转化?(连结AF并延长AF交DC延长线于H点)如图3所示;

②根据情况决定教师介入的程度,比方说:连结AC行吗?……有不同意见吗?

方案二 ①用上节课证明三角形中位线定理的同一法来求证。②转化为平行四边形,如何实现转化?(作平行线,分别过B、F点作BG∥FH∥AD)如图4所示;③根据情况决定教师的介入程度。比方说,过C点作平行线行吗?把梯形ABCD倒过来让一腰重合与原来的梯形组成平行四边形行吗?

4.反思与评价。从上面的学生推导过程中,发现转化思想很重要,但又是什么启发我们用这种思想解决问题呢?是梯形中位线与三角形中位线之间的特殊与一般的联系或梯形与平行四边形的特殊关系。因而在探求梯形中位线性质时,自然就联想到转化为三角形中位线或平行四边形知识来研究。

上述设计不但能帮助学生构建数学思想方法,而且使学生在重新发现数学方法的过程中,其非逻辑思维水平得到提高。

当然,数学思想方法、观念、意识、能力等素质的培养不能仅仅着眼于某一堂课,它是一个潜移默化的过程,是在多次理解和反复应用的基础上逐步形成的,它是数学教学的一项长期任务。