初中数学教学情境的设计研究

潘友勤

教学情境的基本涵义

情境《现代汉语词典》中解释为“情景；境地”。情境含有情形、景象以及环境、境况的意思。《实践教育学》（熊川斌）中指出；情境通常指由特定要素构成的、有一定意义的氛围或环境，它可以由风气、习俗、事件和物质条件等形式来表现。

教学情境是“情”与“境”的融合，这里的“境”是指教学环境，它既可以是一个用实物或多媒体创设的具体环境，也可以指教学双方的关系；“情”是指在“境”中的教学双方人物之间的情感交流、思维互动。教学情境是为了达到既定的教学目标，从教学需要出发，利用具体的场所（教室环境）、景象（课文文境）、境况（学生心境）等来制造或设定与教学内容相适应的场景或师生共同营造的课堂情感氛围，来引起学生的情感体验。

数学教学情境数学教学情境则是指教师根据数学学科特点以及学生数学学习的心理特点，创设各种含有数学知识和数学思想的教学情境。

数学教学情境创设的作用

教学情境对于学生的作用最重要的作用就是改变学生的学习方式。中学生的思维与认识总倾向于直观性和形象化。学习总是与一定的社会文化背景即“情境”相联系的，因为在“情境”的作用下，那些生动直观的形象才能有效地激发学生联想，唤起学生原有认知结构中有关的知识、经验及表象，从而使学生利用有关知识与经验去“同化”或“顺应”当前学习到的新知识，达到对新知识的建构。

教学情境对于教师的作用1）有利于促使教师转变观念，形成新的教学观念。创设情境是在建构主义学习理论指导下的教学活动、教学设计，不仅要考虑教学目标分析、学习者特征分析以及媒体的选择与利用，还要考虑有利于学生建构意义情境的创设问题，并把情境创设问题看作是教学设计的重要内容之一。2）有利于促使教师学习新的教学技术，适应教学模式改革的要求。

数学教学情境创设中存在的主要问题

对教学情境的误解

1）把学生表面的活跃当成成功的情境。创设教学情境的目的之一是为了活跃课堂气氛，调动学生的情绪。但许多时候，学生的活跃仅仅是表面现象，他们只是喜欢好玩的游戏、好听的故事，情境并没有起到增强教学效果的作用，只能作为课堂的装饰或摆设。

例如“多边形”公开课，教师设计20多个问题，学生一个接一个回答问题，教师一问到底，几乎没有对教材进行精讲分析，课堂上似乎显得轻松自如，游刃有余，但学生却疲于应付，杂问碎答，重点不突出，缺少针对性，主次不明，心中疑惑仍在提问中延续。

2）把简单的教学活动当做情境。如把简单的数学问题或者应用题视为情境，将几个极为简单的、挑战性不强的数学问题理解为问题情境；将由生活事例编制而成的应用题理解为生活情境等。

陷入情境的生活化设置误区1）虚构生活实际。将数学知识置于不符合生活实际的情境中，不仅不会使学生感受到生活中有数学，反而让学生认为数学只出现在虚构的生活中，数学是编出来的，是没有用的。2）照搬学生生活例子。部分教师认为将包含数学知识的生活情节搬到数学课堂中来，就是成功地将数学与生活相联系，让学生体验了生活中的数学。

创设的情境没有内涵浮于表面形式，缺乏知识的思考性。创设的情境不能只以情境本身来吸引学生，而应以包含在情境中或由情境引发的知识的思考性，开放性，挑战性来吸引学生，使学生感受数学的魅力，发展数学思维。

教学情境过于丰富、繁琐从教学情境的内容看，所设计的情境情节冗长，出现了过多与教学内容无关的信息，冲淡了情境的主题和主要的教学目标；从教学情境的制作和运作过程看，教师花费了过多的时间和精力创设情境，导致课堂教学效率下降。

再有就是创设的情境模糊不清，缺少科学性。

数学教学情境创设的基本思路与方法

创设实验操作型教学情境思维作为学习过程中智力活动的核心，一般要经过动作思维、形象思维、抽象逻辑思维3个发展阶段，动作思维是一种初级的、基本的思维方式，可以促进其他两种思维的快速发展。而实验就是强调学生通过自己的动手、动脑去制作、设计、发现，通过探讨、归纳、总结，从而发现规律。

创设认知矛盾型教学情境矛盾型问题指问题提示教学内容相关知识之间的矛盾之处，有意识地挑起学生认知中的矛盾，促使学生原有知识与新知识发生激烈的冲突，使学生意识中的矛盾激发，从而产生问题情境，引发学生的思考。如新旧知识的矛盾，日常概念与科学概念的矛盾，直觉、常识与客观事实的矛盾等，都可以使学生处于心欲求而不得，口欲言而不能的“愤”“悱”状态，引起认知冲突，激起学生强烈的探究欲望和学习动机。

创设实践型教学情境实践型情境是指学生从自然、社会文化和生活中根据自己的兴趣选择课题进行自主研究、写出报告或完成作品、进行交流的情境。

创设争论型情境教师故意设错立疑，引发学生争论，学生在争论中思维碰撞，激发兴趣，深化学生对有关知识的认识和理解。同时，也拓展了学生的视野，培养学生的发散性思维。

创设阶梯型教学情境阶梯型教学情境，就是将问题化整为零，层层深入地设置一系列问题的教学情境。它是在学生已有知识仍难以理解有关问题时设置的。

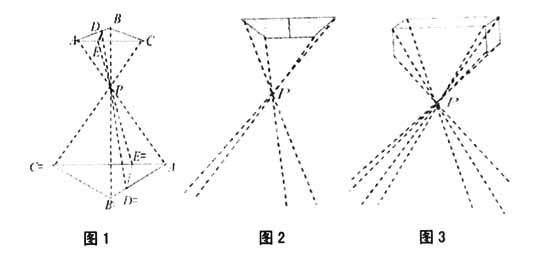
例 1）如图1，经过△ABC三个顶点的三条光线都通过一点P，然后发散出去，在这三条光线经过的地方分别作三个点，依次连结这三个点形成三角形，使作出的三角形与原三角形相似，面积是原来三角形的4倍，怎样画出三角形？这时三角形内的任何线段与对应三角形中的对应线段有什么关系？2）如果定义四边形相似如下：对应边成比例，对应角相等的四边形叫相似四边形，那么你能在图2中画出相似四边形吗？此时，四边形内任一条线段与它对应四边形中的对应线段有什么关系？3）有三边对应成比例的两个三角形相似，那么，四边对应成比例的两个四边形是否一定相似？若相似，说明理由，若不相似，请举反例，然后给出一个用线段定义相似的四边形定义。4）如图3，你能画出与给你的长方体形状相同的长方体吗？5）你能利用灯光把透明照片中的图形进行放大吗？怎样放大？

创设体验数学建模的教学情境 《数学课程标准》指出：强调从学生已有经验出发，让学生亲身经历将实际问题抽象成数学模型并进行解释与应用的过程。

数学教学情境创设需要注意的问题

语言表述、呈现时间和方法等方面的问题1）语言表述上要注意明确具体。心理学研究表明：“教师对问题不同的语言表述，直接影响学生思维的方向和解决问题的方式”。2）注意问题提出的时机与对象的选择。教师创设的问题能否引起学生的积极思考、学生间的讨论，往往取决于提问和选择答题学生的先后顺序。例如，教师一出示问题，就让某位同学回答；提出问题，学生还没有想好，教师就重复问题或重新组织问题或另请一位学生回答，使学生失去信心或减少思维。3）方法上要有目的地创设促使学生提出问题的情境。创设问题情境最终是为了引导学生发现问题。

要注意形成系列化，促进有效延伸教师创设问题情境→学生读懂问题情境→数学问题，会多花时间。思考：能否在一节甚至在一章内容的学习中用同一个问题情境？

例 “字母表示数”一章，起始课的情境引入——用火柴棒摆正方形的活动，不仅解决了字母表示数引入的必要性问题，还引出代数式的概念，以及后续的代数式求值、合并同类项的内容的学习。

必须体现数学化的过程数学化是指学生从自己的数学现实出发，经过自己的思考得出有关数学结论的过程。数学活动就是学生学习数学，探索、掌握和应用数学知识的活动。数学活动不是一般的活动，而是让学生经历数学化过程的活动。

精心创设数学教学情境，开发课程资源数学教学情境是以问题为核心形成的教学氛围，在教学中要围绕问题转，在发现问题、提出问题、解决问题的过程中，让学生的能力得到培养。因此，数学教学情境也是不可缺少的课程资源。

（作者单位：浙江省玉环县坎门一中）