傅里叶变换与反变换在点阵图像信息压缩处理中的应用

张　淼

【摘要】本文采用MATLAB软件编写程序，利用一维或二维的傅里叶变换函数，实现了对二维图像信息的傅里叶变换，通过程序对其频谱结果进行处理，利用傅里叶反变换函数，实现了对二维图像信息的压缩，进而展示了傅里叶变换与反变换在信号的时域、频域处理方面的作用。本文有助于对信号处理原理的学习与理解。

【关键词】二维信号 二维离散 傅里叶变换 傅里叶反变换 图像压缩 MATLAB

一、引言

对信号的分类，可以从不同的角度进行，通常可以分为时域信号、频域信号，一维信号、二维或多维信号，连续信号、离散信号等。将信号采用数学函数表达式表示，给信号的连续性、确定性的研究提供了必要的研究基础，而常见的一维或二维的信号，如连续的一维声音信号、连续的二维图像信号，它们在时域上离散表示时，通常采用相关的数据表示。本文研究的内容，主要是时域上离散的二维图像信号数据与其频域信号的变换、处理问题。

二、二值化离散

对于二维离散数据可以理解为：它们原先是时间函数在一定采样频率下离散的结果。对一张图像、一个指纹、一个汉字等二维平面上的信息采样，可得到二维离散数据。离散后的数据，一般为正实数内的数据，为简便起见，下面对一个汉字进行二维数据进行二值化离散，即非0即1的离散。

将汉字“王”字的二维二值化数据，可用如图1(a)所示的矩阵描述，在f(m，n)矩阵中，将汉字中的笔画上的点用“1”表示，无笔画的地方用“0”表示。图1(b)为将图1(a)中“0”去掉以后的情形，由此可见，图1(a)所示的矩阵能基本表示出“王”字的信息。当然，点阵数越多，所描述出的汉字信息也越多，准确性越好，失真越小。

图1 “王”字的16*16点阵矩阵

对二维连续信号的傅里叶变换，定义为

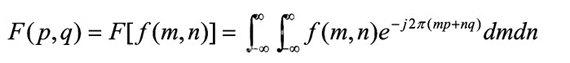(1)

其中p、q为空间频率，通常f(m，n)为空间频率的复数值函数，它也有模值与相角，其模值为二维幅度谱(能量谱、密度谱)。由于式(1)可表示为

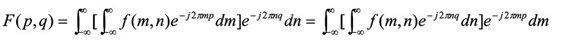
因此，对二维连续信号f(m，n)的傅里叶变换可视为先沿一个方向进行一维的傅里叶变换，再沿另一个方向进行一维的傅里叶变换。同理，对傅里叶反变换也可以两次按一维进行。

与一维连续傅里叶变换相似，式(1)为二维连续信号的傅里叶变换，要想用计算机处理，必须将其离散化，二维离散傅里叶变换为

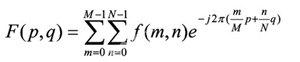(2)

式(2)中，离散矩阵f(m，n)的行与列为M行、N列，M与N可以不相等，但都为正整数。如在图1中M=N=16。

三、软件实现

在MATLAB软件中，对一维数组a进行傅里叶变换使用函数fft(a)进行，对二维数组c进行傅里叶变换，可以利用对一维数组进行傅里叶变换的函数，进行二维数组的傅里叶变换函数，其形式为：fft(fft(c).′).′，也可以直接利用对二维数组的傅里叶变换函数fft2(c)进行；对二维数组c的傅里叶反变换函数，其形式为ifft2(c)。下面的MATLAB程序实现对图1所示的二维离散数据的进行显示、傅里叶变换、能量谱的显示、频谱压缩、傅里叶反变换、还原显示等处理，程序行右边以“%”开头的是程序的注释。

imshow(f，'notruesize')%显示矩阵f点阵图，如图2所示。

a=input('aaaaa=')%等待从命令窗口输入任意数，目的是看清图2结果。

F = fft2(f)；%对矩阵f进行2维傅里叶变换，赋值到F中

F0=F；%将F保存到F0中，后续还要用到F

F1 = log(abs(F))；%对变换结果取模值，并取常用对数，数越大，幅度越强

imshow(F1，[-1 4]，'notruesize')；%以五种颜色显示频谱，

colormap(jet)； colorbar%结果如图3所示

a=input('bbbbb=') %等待从命令窗口输入任意数

由图3可知，频谱的中心部分对应图像的高频分量，其能量较低，它们在傅里叶变换反变换中作用较小，为此，可将中心部分的频谱去掉，清空为零，，然后进行傅里叶变换反变换，得到点阵图案。为此，可继续执行如下程序。

for i=8：1：10；%对第8到第10行

for j=6：1：12；%对第6到第12列

F( i，j )=0；%频谱的中间清空(为0)

end%列循环结束

end%行循环结束

f1=ifft2(F)%对中空的频谱做傅里叶反变换

f2=abs(f1)%对变换结果取绝对值，因为变换结果为有正、负的实数

imshow(f2，'notruesize') %将矩阵f2中的数据显示出来，结果与图2完全相同

a=input('cccccc=')%等待从命令窗口输入任意数，目的是看清图的结果

从中空的频谱的反变换所得到的点阵图像与原点阵图像相同这一点说明，二维数据的频谱从能量上看，主要分布在边缘部分，如果将原频谱F0的四角重新组织在一起，从16*16频谱矩阵F0生成一个新的8*8频谱矩阵F2。

这样处理，实际上就是实现了频谱压缩，将压缩的频谱进行傅里叶变换反变换，得到压缩一般的点阵图案，为此，可继续执行程序(程序略)。

由图4可见，这是一个非二值化的灰度图象，已基本上看不清是一个“王”字，因为在f4矩阵中的数据尽管是实数，但并非是非0即1的数据，为此，要进行二值化处理，将高于某个数值的认为是1，而低于某个数值的认为是0，这个数值即阈值。对阈值的选择，可取f4矩阵中的数据的平均值。

四、结论

通过程序执行发现，用平均值作阈值所得到的图像并不是十分理想，而当阈值y=2.53~2.71时，形成的压缩图像保持一致，如图6所示。比较图2原16*16点阵图与图6压缩8*8点阵图，压缩图笔画信息稍有失真。可见，还原阈值的选择十分重要。

以上例子显示了利用傅里叶变换与反变换函数，对二维图像信息的压缩处理与还原的具体应用，展示了傅里叶变换与反变换在信号的时域、频域处理方面的作用。

参考文献：

[1]程佩青.数字信号处理教程[M].北京：清华大学出版社，2001，8.

[2]樊昌信.通信原理[M].北京：国防工业出版社，2008，3.