引导学生体验生活培养数学应用能力

柯家文

摘要：数学教学不仅仅是知识的教学，更是一种过程教学、体验教学。密切数学与生活之间的联系，突破学科本位，体现教学生活化、活动化和情感化是数学新课程强调的重要教学目标。通过学生亲自动手操作，经历观察、记录、整理、分析、交流，加之于小组的密切合作，能够更好地感受数学、体验数学、应用数学。关键词：数学体验；探索；问题意识；生活情景；培养

爱因斯坦说过：“对一切来说，只有热爱才是最好的老师。”在数学教学中，教师要努力挖掘数学与生活的联系，将教学组织的深入浅出，生动有趣，让学生感受到数学就在我们身边，无处不在，无处不有。

一、观察身边事物，触动生活积累，让学生感受数学

课程内容的设计要力求从生活实际出发，从学生熟悉的感兴趣的问题引入学习的主题，创设丰富的问题情境，用心营造一种学生能独立思考。大胆质疑，积极主动参与的教学氛围。实践表明，学生有了强烈的问题意识，才会深入思考，才能创造性地提出问题和解决问题。

从学生身边的数学问题引入，充分激发学生的思维，既要求学生从实践中归纳结论，又要求学生把发现的结论用自己的文字语言或数学语言表达出来，尽可能让抽象的数学概念在生活中找到原形。在教学中可充分运用网络资源，选用富有生活情趣的动画、图景、贴近学生的生活的实例制作课件，沟通书本知识与现实生活的联系，调动学生学习的积极性、主动性，点亮学生智慧的火光，使学生觉得学数学是有趣的、有用的，并热爱数学。

案例1：《直线与圆的位置关系》的教学。上这节课的时候，以“同学们看过海上日出吗?”引入新课，把同学们的思绪带到广阔的大海边，在大脑的荧光屏上放映出太阳从海平面慢慢升起的画面。然后引导学生按照以下三个步骤进行：

(1)勾勒生活形态：请同学们先在脑子里勾勒出太阳从海平面慢慢升起直至离开海平面的轮廓。

(2)抽象数学模型：学生说脑子里出现了蓝色的平静的海平面，红色的朝阳。海平面的尽头象是一条直线，红色的太阳象是一个圆。

(3)总结认知规律：利用多媒体课件放映日出的全过程并把太阳抽象成一个圆，海平面抽象成一条直线，进而让学生讨论圆与直线有几种位置关系?再用几何画版放映出圆与直线的位置关系的变化过程，最后归纳出圆与直线的相切、相交、相离的三种相对位置关系。该节课运用这种“生活化”的新课引入法取得了很好的效果。

教师所引入的生活画面与形态越逼真，学生学习就越有兴趣，理解得就越深刻，同时还培养了学生的想象力，激发了学生的学习主动性。

二、联系日常生活，突出应用意识，让学生体验数学

探索是人类思维中最活跃、最生动、最富有魅力的活动。探索的结果往往导致问题的解决和新的发现。无论是布鲁纳主张的发现法，还是玻利亚倡导的数学启发法，其精髓都是重在让学生学会探索，学会发现。如布鲁纳所倡导的，不是把学习材料直接星现给学生，而是给出一些提示性的线索，通过问题启发，做一做，想一想，试一试，议一议等方式，让学生自己通过积极主动的探索活动来学习数学，提高学生的实践探索能力。

现代心理学认为：教学时应设法为学生创设逼真的问题情境，唤起学生思考的欲望。荷兰著名教育家弗霄登塔尔指出，要从学生的生活实际中发现和创造，即强调从学生熟悉的生活环境和生活经验出发进行教学。让学生置身于逼真的问题情境中，体验数学学习与实际生活的联系，品尝到用所学知识解释生活现象以及解决实际问题的乐趣，感受到借助数学的思想方法，解释生活中常见的各种数学现象，如优惠措施、行程问题的最佳选择、物品的分配等。《数学课程标准》指出，数学教学必须注意从学生的生活情境和感兴趣的事物出发，为他们提供参与的机会，使他们体会到数学就在身边，对数学产生亲切感。

案例2：甲乙两商店以同样价格出售同样的商品，并且各自推出不同的优惠方案：在甲店累计购买100元商品，再购买的商品按原价的90％收费；在乙店累计购买50元商品后，再购买的商品按原价的95％收费。

学生活动1——独立思考以下几个问题：

1、现有4个人，准备消费40元，80元，140元，160元，那么去哪家商店更合算，为什么?

2、甲商店购物款达多少元可以优惠?乙商店购物款达多少元可以优惠?

通过简单数据的比较，学生猜想到：

①若劣汁购物不超过50元，则在两家商场花费是一样的。

②若累计购物超过50元，但不超过100元，则在乙商场购物花费小。

③若累计购物超过100元又可能存在有三种情况。

学生活动2——继续分组讨论结论③：(1)什么情况下，在甲商场购物花费小?(2)什么情况下，在乙商场购物花费小?(3)什么情况下，在两家商场购物花费相同?若累计购物超过100元时，分别在什么情况下甲优惠、乙优惠、甲乙费用相等?

教师分析——设消费x元时(x>100)分别表示甲店、乙店的费用。根据哪个店优惠，即该店费用便小于另一个店的费用，于是建立不等关系。学生在教师启发引导下得出结论③即累计购物超过100元而不到150元时，在乙商店购物省钱，累计购物恰好150元时，两个商店购物花费一样，累计购物超过150元时，在甲商店购物省钱。

学生独立思考并归纳——根据甲、乙商店的销售方案，顾客怎样选择商店购物能获得更大优惠?你能为消费者设计一套方案吗?

通过体验如何选择商场购物，感受实际生活中存在的不等关系，根据实际问题中的不等关系列出不等式，就把实际问题转化为数学问题。这样，学生就走出了从数学到数学的圈子，从生活中找数学，学生活中的数学，感受到数学是生活中处处存在的，学习数学是为了解决生活中的实际问题，使学生增强学习兴趣，提高他们学习的积极性，调动学生学好数学的原动力。

三、注重动手实践，解决生活问题，让学生应用数学

一个人数学素质的优势不在于其掌握数学知识的多少，也不在于其能解决多少数学难题，而在于他能不能应用数学知识去解决实际问题。构建学生数学应用的理念，是教学中必不可少的一个环节，在课堂教学中占有重要的地位。数学新课程体现了数学刻画现实世界的过程和全貌，教师应在数学课程和教学中努力为学生提供生活背景和实践机会。使学生逐步形成数学应用意识和应用能力。

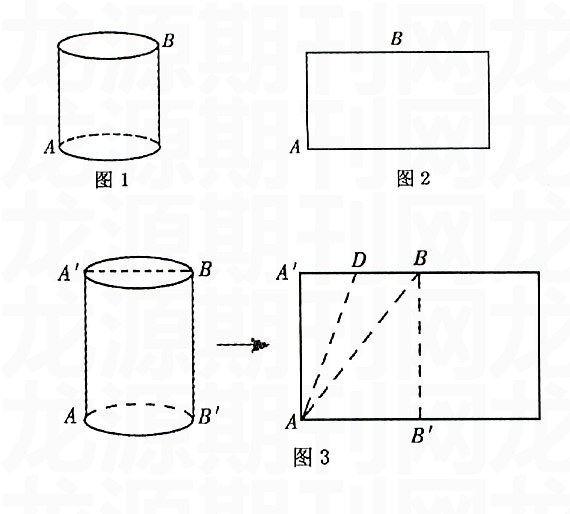
案例3：为了让学生能够真正掌握“圆柱的侧面展开图”数学知识的应用，在教学中呈现“蚂蚁怎么走最近?”这一鲜艳活泼的生活问题：

如图1，有一个圆柱，它的高等于12厘米，底面半径等于3厘米。在圆柱形的底面A点有一只蚂蚁，它想吃到上底面上与A点相对的B点处的食物，需要爬行的最短路程是多少?(π的值取3)。

(1)同学们可自己做一个网柱，尝试从A点到B点沿圆柱的侧面画出几条路线，你觉得哪条路线最短呢?(小组讨论)

(2)如图2，将圆柱侧面剪开展开成一个长方形，从A点到V点的最短路线是什么?你画对了吗?

(3)蚂蚁从A点出发，想吃到B点上的食物，它沿圆柱侧面爬行的最短路程是多少?(学生分组讨论，教师公布结果并讲解)

我们知道，圆柱的侧面展开图是一长方形。好了，现在咱们就用剪刀沿母线AA将圆柱的侧面展开(如图3)。

我们不难发现，刚才几位同学的走法：(1)A→A′→B；(2)A→B′→B；(3)A→D→B；(4)M→B。

哪条路线是最短呢?你画对了吗?第(4)条路线最短。因为“两点的所有连线中，线段最短”。

经过练习。学生发现这是一道与生活密切相关的问题。可见，学生经常接触与生活联系密切的数学问题，就会在现实生活中真正懂得如何应用数学。

当然，学生应用意识的提高还不能局限于某个知识点的应用上，由于学科活动本身具有的综合性，所以只有通过设计与社会生活密切联系的教学活动才能激发学生的学习兴趣，增强应用的能力。例如，学习了解三角形后，让学生测量学校旗杆的高度，测量山高；学习从部分看整体的教学中，可以组织学生到社会中调查某一种情况，引导学生收集数据，对数据进行整理、分析，得出结论；在制作剪纸和镶边的过程中，进一步理解轴对称及其性质，体验轴对称在现实生活中的广泛应用和丰富的文化价值等。这样的实践活动，更贴近学生生活。学生的应用能力得到了提高，思维得到了发展，数学整体素质也得到了提高。

综上所述，只有在数学教学中强调从学生身边的行为、自身的活动出发，激发学生对活动的参与热情和学习兴趣，才能体验到生活中的数学，实现数学的应用价值，达到培养学生的主动性和创造性的目的。

参考文献：

[1]黄新民_初中数学课堂创新教学理论与实践[M]，杭州：浙江大学出版社，2004

[2]数学课程标准研制组编写，数学新课程标准(实验稿)解读[M]，北京：北京师范大学出版社，2002

[3]课程教材研究所，中学数学课程教材研究开发中心，课程教学设计与案例[M]，北京：人民教育出版社，2004