高中数学课程标准对学生数学素养的要求
苏洪雨 吴周伟
在现代社会,人们日益离不开数学,因此具有一定的数学素养是现代公民适应生活、工作的必要条件。高中数学教育在培养学生的数学素养方面起着举足轻重的作用,作为义务教育后的数学教育,高中数学包含了数学体系中最基本的内容,同时又和深层次的数学紧密相连,它在学生的数学学习过程中,有着承上启下的过渡作用,而且有可能是学生最终的学校数学教育。所以,高中数学使学生获得必要的数学素养至关重要。2003年的《普通高中数学课程标准(实验稿)》(以下简称:《标准》)在课程总目标中提出:使学生在九年义务教育数学课程的基础上,进一步提高作为未来公民所必要的数学素养,以满足个人发展与社会进步的需要。
那么,具体来说,《标准》对培养学生数学素养提出哪些要求?这些要求对于数学课程的发展和数学教学有着怎样的影响?在学校数学教育中,如何结合教学实践培养学生的数学素养?
一、 数学素养的内涵
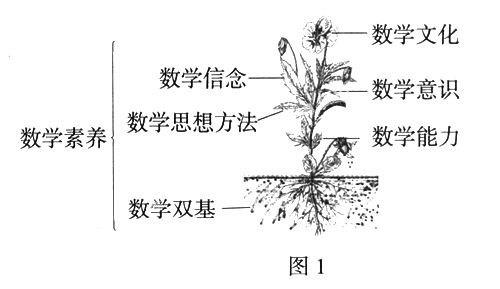
关于数学素养,人们有着不同的理解和认识。“MA”课题组(1997)认为,数学素养是指以人的先天生理特点为基础,在后天的环境和数学教育影响下形成并发展的心理方面的稳定属性。王子兴(2002)认为,数学素养是数学科学所固有的内蕴特性,是在人的先天生理基础上通过后天严格的数学学习活动获得的、融于身心中的一种比较稳定的状态,……是一种心理品质。朱德全(2002)认为数学素养的生成是个体在已建立数学经验基础之上对数学感悟、反思和体验的结果。在《普通高中数学课程标准解读》中,数学素养是一种基本的文化素养,……基础教育数学课程的基本目标就是要提高学生的数学素养。由此,我们发现,上述的认识(包括标准),都把“数学素养”作为一种“人们内隐的、逐步形成的”能力、素质或者修养,它是一种学生在数学方面的抽象的综合表现。《标准》认为高中数学课程是培养学生素质的基础课程,提高学生的数学素养可以从六个方面进行:数学双基、数学思想方法、数学能力、数学意识、数学信念和数学文化。这六个方面是紧密相连,互不分割,共同发展;通过具体的数学内容,在问题情境中展现出学生的数学素养。因此,我们可以用一个图形来表示他们彼此的关系。(如图1所示)
1.数学双基
数学双基包括:数学基础知识和基本技能。知识和技能是学生在数学上发展和进步的土壤,依托数学知识,掌握基本的技能,才能培养学生的数学能力、数学信念,了解和理解数学思想方法,从而体验数学文化的无穷魅力。
2.数学能力
数学能力是学生在进行数学活动的过程中,逐步形成的一种心理特征。《标准》认为在高中阶段,数学能力包括空间想象、抽象概括、推理论证、运算求解、数据处理等基本能力,以及数学地提出、分析和解决问题(包括简单的实际应用问题)的能力,数学表达和交流的能力,还有独立获取数学知识的能力。数学能力是数学素养的重要组成部分,当人们进行相关的数学活动时,数学能力就外显出来。培养学生的数学能力也是数学教育的一个重要目标,如果把知识和技能看作学生发展的基石,那么数学能力将是帮助学生解决问题的助推剂。
3.数学思想方法
数学思想方法是指关于数学自身的论证、运算以及应用的思想、方法和手段,除此之外,还包括关于数学(其中包括概念、理论、方法与形态等)的对象、性质、特征、作用及其产生、发展规律的认识。同一个数学思想,当用它去解决别的问题时,就称之为方法,当评价它在数学体系中的自身价值和意义时,就称之为思想。数学知识是数学学习过程中的载体,而技能是处理知识的基本操作过程,但是蕴含在知识和技能之中的就是重要的数学思想方法。
4.数学意识
我们把应用数学的意识和创新意识称之为数学意识;也可以说,这是对数学的一种感觉。在生活实践应用数学过程中,有的人可以熟练地运用数学思想方法和数学工具,有的却只能就事论事,不能从数量关系或者空间位置中发现问题的本质,两者不同的表现就是数学应用意识的不同。再者就是创新意识,在学习数学和应用数学过程中,善于发现其中的数学模式,尝试使用不同的数学方法解决问题,从思想和观念上开拓创新,这就是创新意识。
5.数学信念
数学信念也可以称之为数学观,就是对数学的基本看法,数学是什么?有用的,没用的?有趣的,还是枯燥的?学生有没有学习数学的信心和毅力?等等。这都是关于数学信念的问题,同时这也是数学素养的重要组成部分。
6.数学文化
数学是一种文化,张奠宙先生认为,“数学文化在特定的社会历史下,数学团体和个人在从事数学活动时,所显示的民族特征、传统习惯、规则约定、以及思想方法等的总和。”郑毓信先生指出:“数学作为文化的特殊性在于数学对象的形式建构性与数学世界的无限丰富性和秩序性”。《标准》对数学文化有这样的阐述:“数学是人类文化的重要组成部分。数学是人类社会进步的产物,也是推动社会发展的动力。”学生的数学素养不仅体现在数学地解决问题、良好的数学意识以及正确的数学信念,还体现在能够欣赏数学的价值,展示一定的数学文化气息。
二、 标准对数学素养的要求
数学素养是一种个人蕴含的内在品质或者能力,《标准》没有对数学素养提出直接的要求,正如图1,我们希望这棵树苗能够茁壮成长,但不能对这个树苗提出什么要求。《标准》认为,高中数学课程对于认识数学与自然界、数学与人类社会的关系,认识数学的科学价值、文化价值,提高提出问题、分析和解决问题的能力,形成理性思维,发展智力和创新意识具有基础性的作用,也是学习其他学科的基础,它为学生的终身发展,形成科学的世界观、价值观奠定基础,对提高全民族素质具有重要意义。
《标准》对学生在数学方面的最终目标是:希望学生能够提高必要的数学素养。这是一种综合性的要求,这种综合性的要求可以在学生面对现实情境,运用数学处理问题时,得到检验。例如。
一家汽车公司与某出口商定了一个合同:在一段相当长的时间内,每天至少把60辆汽车运到指定的港口,准备出口。公司使用A和B两种类型的运输车,A型运输车能装运10辆汽车,B型运输车能装运8辆汽车。现在公司有4辆A型运输车和6辆B型运输车,但只有8个司机能工作。如果运输车每天只能运一次,那么每天最多能运多少辆汽车?每天最少需要多少个司机?面对这样的问题,学生要有一定的数学意识,不仅能从情境中抽象概括出数学语言,还要寻找蕴含的数学模式,应用适当的数学思想方法解决问题。当然,这一切都离不开数学的基础知识,也不能脱离基本的数学技能。在解决类似问题的过程中,学生逐步建立数学信念,体验数学文化。
1.获得数学知识技能,掌握数学思想方法
数学基础知识和数学基本技能是培养学生数学素养的载体,在进行数学双基的教学过程中,不断渗透数学思想方法;通过处理各种和数学相关的问题,培养学生的数学能力,进而提高数学意识和文化修养。因此,《标准》指出,获得必要的数学基础知识和基本技能,理解基本的数学概念、数学结论的本质,了解概念、结论等产生的背景、应用,体会其中的数学思想和方法,以及它们在后续学习中的作用。
例如,《标准》有这样的例子。
观察自己的教室,说出观察到的点、线、面之间的位置关系,并说明理由。
那么,必要的数学知识就是关于空间立体几何的基本定理。
公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内。
平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行。
一个平面内的两条相交直线与另一个平面平行,则这两个平面平行。
一条直线与一个平面内的两条相交直线垂直,则该直线与此平面垂直。
一个平面过另一个平面的垂线,则两个平面垂直。
……
在具备一定的数学知识的基础上,必要的基本技能也有助于学生在数学上进一步发展。技能包括快速且准确地进行计算,逻辑地进行数学的基本论证。《标准》认为,随着时代的发展,数学课程要重新审视“双基”。
数学双基赋予学生知识和技能,但是进行数学地理解是一个必不可少的过程,只有理解了,学生才能认识到数学思想方法的重要性,才能在实践中应用数学思想方法解决问题。理解数学就要领会数学概念的内涵,了解数学公理、定理的本质和背景,通过进行数学探究、发现学习、再创造等过程,掌握数学思想方法,不断深化数学的理解。
掌握数学思想方法,是指掌握蕴含在数学知识和技能中的精髓。富兰克林在18世纪中叶提出过:“可惜知识是无穷的,而学生的时间却是有限的。”事实上,在学生离开课堂,走入社会,如果不是从事和数学紧密相关的行业,真正记住的数学知识并不多,但是一些重要的数学思想方法却让他们难以忘却,在自觉与不自觉中,归纳、演绎、类比、分析、综合等逻辑推理都得到了运用。《标准》在课程的基本理念中强调:使学生理解数学概念、结论逐步形成的过程,体会蕴涵在其中的思想方法。
2.提高基本数学能力,逐步培养数学意识
如果把数学知识和技能看作植物的根部,也就是数学素养的发展基础,那么,数学能力应该是植物的主干,在数学能力的支配下,学生才可以进行各种数学活动,同时结合重要的数学思想方法,学生可以合理地利用数学解决问题。我国在以往的数学教学大纲中有运算能力、逻辑推理能力和空间想象能力之说,后来又加上了运用数学知识分析和解决实际问题的能力。在社会发展的新时代,《标准》与时俱进,在原来的基本数学能力上,新增了抽象概括能力和数据处理能力。在一般能力上,除了数学地提出、分析和解决问题(包括简单的实际应用问题)的能力,还增添了数学表达和交流的能力,独立获取数学知识的能力。在课程的基本理念中,强调注重提高学生的数学思维能力,其中包括:直观感知、观察发现、归纳类比、空间想象、抽象概括、符号表示、运算求解、数据处理、演绎证明、反思与建构等思维能力。
《标准》认为,学生数学能力的获得在提高自主学习、实现可持续发展中至关重要。数学能力是学生数学素养形成的重要因素,它可以通过了解学生对知识的掌握和运用水平体现出来。学生数学能力是在数学知识建构和问题解决过程中逐步获得的。例如可以从课堂数学学习、数学探究和建模活动中,培养学生发现问题和提出问题的能力;再者通过联系相关的数学知识,提出问题解决的思路,建立恰当的数学模型,尝试解决问题,培养学生有效的收集信息的能力。在这些过程中,要训练学生独立思考,和他人合作交流,清晰的数学思想表达能力。
数学意识是学生在数学学习和进行数学问题解决过程中逐步发展起来的。《标准》要求,发展数学应用意识和创新意识,力求对现实世界中蕴涵的一些数学模式进行思考和做出判断。例如在学习计数原理、统计案例、概率等内容中,学生要“能用所学知识解决一些简单的实际问题,进一步体会概率模型的作用及运用概率思考问题的特点,初步形成用随机观念观察、分析问题的意识。”再如在“数学建模”过程中,学生将体验数学在解决实际问题中的价值和作用,体验数学与日常生活和其他学科的联系,体验综合运用知识和方法解决实际问题的过程,增强应用意识;激发学生学习数学的兴趣,发展创新意识和实践能力。
3.树立良好数学信念,体会数学文化价值
良好的数学信念在学生学习数学,形成数学素养过程中起着积极的推动作用。数学信念会影响学生的学习和学习成果,包括他们对数学之认识、理解和表现。《标准》要求:提高学习数学的兴趣,树立学好数学的信心,形成锲而不舍的钻研精神和科学态度。数学信念就是学生对数学的情感态度问题。著名的数学家华罗庚教授认为:“就数学本身来说,也是壮丽多彩,千姿百态,引人入胜的。一个问题想不出来时,固然有些苦恼,若一旦豁然想通,那滋味难道不是甜蜜蜜的,这和音乐,舞蹈艺术的享受有何不同?”《标准》制定者指出:对学习产生兴趣,树立学好数学的信心,是学生和未来公民应该具备的一种重要素质,……同其他学科相比,数学课程的学习更需要一点精神,需要锲而不舍的钻研精神,需要有克服困难的意志力和决心,因而数学课程也就成为我们培育学生具备这种精神和态度的很好的载体。《标准》建议可以从教材的编写,案例的引入等方式来激发学生数学学习兴趣,培养学生良好的数学信念。
数学是人类文化的重要组成。在新课程中,尤其重视数学文化的教学。数学文化、数学探究和数学建模贯穿于整个高中数学课程,渗透在每个模块或专题中。《标准》希望学生通过在高中阶段数学学习,初步了解数学与人类社会发展之间的相互作用,体会数学的科学价值、应用价值、人文价值,开阔视野,寻求数学进步的历史轨迹,激发对于数学创新原动力的认识,受到优秀文化的熏陶,领会数学的美学价值,从而提高自身的文化素养和创新意识。
例如在学习导数及其应用的内容时,希望学生体会导数的思想及其丰富内涵,感受导数在解决实际问题中的作用,了解微积分的文化价值。再如,在二项式定理中介绍我国古代数学成就“杨辉三角”,在统计案例中介绍所学统计方法在社会生活中的广泛应用,以丰富学生对数学文化价值的认识。
三、 总结
在《标准》看来,数学素养是学生在数学学科上的综合素质。国际教育成就评价协会(IEA)在TIMSS 2003测试中,从对基本事实和过程的了解、概念的使用、解决常规问题和说理四个不同的认知水平层次对学生的能力进行测评。而国际学生评价项目PISA认为:数学素养是一种个人能力,学生能确定并理解数学在社会所起的作用,得出有充分根据的数学判断和能够有效的运用数学。这是作为一个有创新精神、关心他人和有思想的公民,适应当前及未来生活所必须的数学能力。对照三者,其实有着很多类似的地方,数学素养就是学生在数学问题情境中,应用数学的过程所表现出来的数学能力、数学信念,也包含着数学思想方法的运用,对数学的欣赏,体会其价值等。数学素养的这些元素相互联系,不可分割;反之,学生在数学知识技能、数学能力等的发展对培养学生的数学素养也有着至关重要的影响。
《标准》对学生在数学上的表现提出了一个整体性的要求,这对于学生的发展数学素养有着积极的意义,同时也为我们的数学教学提供了一个明确的方向,而对教师来说也提出了更高的要求。
参考文献
[1] 中华人民共和国教育部. 《普通高中数学课程标准》(实验).北京:人民教育出版社,2003,4.
[2] “MA”课题组.“发展学生数学思想,提高学生数学素养”教学实验研究报告.课程·教材·教法,1997(8):35~39.
[3] 王子兴.论数学素养.数学通报,2002(1).
[4] 朱德全.数学素养构成要素探析.中国教育学刊.2002,49~51.
[5] 严士健等.普通高中数学课程标准解读.南京:江苏教育出版社,2004.2.
[6] 解恩泽,徐本顺主编.数学思想方法.济南:山东教育出版社,1989,11.
[7] 王林全.中学数学思想方法概论.广州:暨南大学出版社,2000,10.
[8] 张奠宙.中学数学中的文化涵义.宁波:教育部数学教育高级研讨班发言稿,2007.4.
[9] 郑毓信.数学文化学.成都:四川教育出版社,2001.11.
[10] 上海中小学课程教材改革委员会.数学.(文科高中三年级).上海:上海教育出版社,2004.8:26.
[11] 布鲁纳.邵瑞珍译.教育过程.北京:文化教育出版社,1982.6.
[12] 黄毅英.数学观研究综述.数学教育学报.2002(11).
[13] 华罗庚等.数学家谈怎样学数学.哈尔滨:黑龙江出版社,1986.9.
[14] 江春莲.TIMSS系列研究简介(1).数学通讯,2006(9).
[15] 黄惠娟等.PISA:数学素养的界定与测评.上海教育科研,2003(12).
(责任编辑刘永庆)

