识别菱形三策略

房延华

菱形是一种特殊的平行四边形,也是一种近似“完美”的四边形,因为它具有很多特殊的性质.如何识别菱形?我们可以从以下几个方面去考虑.

一､从菱形的定义考虑

例1(2007年·娄底)如图1,已知点D在△ABC的BC边上,DE∥AC交AB于点E,DF∥AB交AC于点F.

(1)试说明:AE=DF;

(2)若AD平分∠BAC,试判断四边形AEDF的形状,并说明理由.

分析 由平行四边形的性质容易得出AE=DF.由DE∥AC,DF∥AB,可知四边形AEDF为平行四边形,再利用AD平分∠BAC可得出AF=DF,故由定义可判定四边形AEDF为菱形.

解:(1)∵ DE∥AC,DF∥AB,∴四边形AEDF为平行四边形.

∴AE=DF.

(2)若AD平分∠BAC,则四边形AEDF是菱形.理由如下.

由(1)知四边形AEDF是平行四边形.

∴∠BAD=∠ADF.

∵AD平分∠BAC,∠BAD=∠DAF,∴∠DAF=∠ADF.

∴AF=DF.

∴ AEDF为菱形.

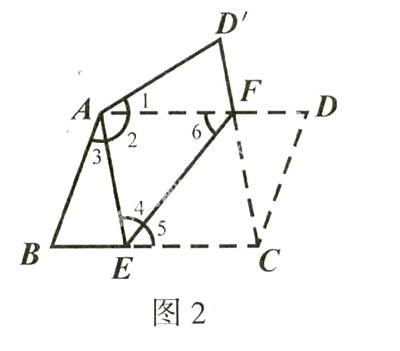
例2(2007年·青岛)将平行四边形纸片ABCD按如图2的方式折叠,使点C与点A重合,点D落到点D′ 处,折痕为EF.

(1)求证:△ABE≌△AD′F;

(2)连接CF,判断四边形AECF是什么特殊四边形.证明你的结论.

分析 由边角关系易证△ABE≌△AD′F.猜想四边形AECF是菱形.由轴对称性质知AE=EC,从而只需再判定四边形AECF是平行四边形即可.

解:(1)由折叠性质可知:∠D=∠D′,CD=AD′,∠BCD=∠D′AE.

∵四边形ABCD是平行四边形,

∴ ∠B=∠D,AB=CD,∠BCD=∠BAD.

∴ ∠B=∠D′.AB=AD′.∠D′AE=∠BAD,即∠1+∠2=∠2+∠3.

∴ ∠1=∠3.

∴ △ABE ≌△A D′F(ASA).

(2) 猜想四边形AECF是菱形,证明如下.

由折叠可知:AE=EC,∠4=∠5.

∵ 四边形ABCD是平行四边形,∴AD∥BC.∠5=∠6.

∴ ∠4=∠6. AF=AE.

∵AE=EC,∴ AF=EC.

又∵ AF∥EC,∴ 四边形AECF是平行四边形.

∴ AECF是菱形.

点评:利用定义判定菱形时,一般先证明四边形是平行四边形,再利用条件找出一组邻边相等.如果已知有一组邻边相等,则只需让四边形为平行四边形即可.总之,两个条件缺一不可.

二､从四条边的数量关系考虑

通过判定四边形的四条边相等,来说明四边形为菱形.

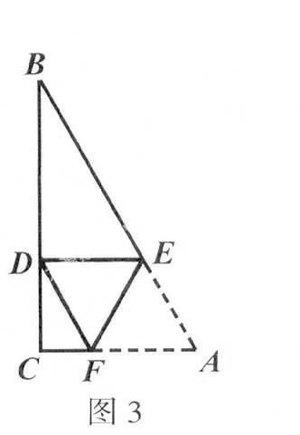
例3 (2007年·巴中)如图3所示,在Rt△ABC中,∠C=90°,∠A=60°.点E､F分别在AB､AC上.把∠A沿着EF对折,使点A落在BC上点D处,且使ED⊥BC.试说明四边形AEDF是菱形.

分析 由折叠的性质和等边三角形可得出很多相等的边,所以可利用四边相等来证明四边形AEDF是菱形.由轴对称性质知:AF=DF,AE=DE.从而只需再判定AE=AF即可.

解:由折叠性质可知:AF=DF,AE=DE,∠AEF=∠DEF.

∵ ∠C=90°,∠A=60°,∴ ∠B=30°.

又∵ ED⊥BC,∴ ∠BED=60°.

∴ ∠AEF=∠DEF=1/2(180°-∠BED)=60°.

∴ △AEF为等边三角形.AE=AF.

∴AF=DF=AE=DE.四边形AEDF为菱形.

点评:利用四边相等证明菱形,一般是利用轴对称或三角形全等等知识.另外值得注意的是,两个全等的等边三角形可以“拼成”菱形.

三､从对角线的角度考虑

通过判定四边形的对角线互相垂直平分,来判定四边形为菱形.

例4(2006年·张家界)如图4,已知ABCD的对角线AC､BD相交于点O.BD绕点O顺时针方向旋转,交AB､DC于点E､F.

(1)试说明:四边形BFDE是平行四边形.

(2)BD绕点O顺时针方向旋转多大角度时,四边形BFDE为菱形?请说明理由.

分析 根据题目的特点,本题应把握与对角线有关的两个判定:(1)对角线互相平分的四边形是平行四边形;(2)对角线互相垂直的平行四边形是菱形.

解:(1)因为四边形ABCD是平行四边形,所以OB=OD,AB∥CD,所以∠OBE=∠ODF.

又∠BOE=∠DOF,所以△BOE≌△DOF(AAS).

所以OE=OF.而OB=OD,所以四边形BFDE是平行四边形.

(2)BD绕点O顺时针方向旋转90°时,四边形BFDE是菱形.

理由:因为∠DOF=90°,所以EF⊥BD.又因为四边形BFDE是平行四边形,所以四边形BFDE为菱形.

点评:通过对角线互相垂直平分判定菱形,其实质是先利用对角线互相平分判定平行四边形,再利用对角线垂直判定菱形.