“函数的单调性”教学设计

教学目标

认识目标：掌握函数单调性的概念；会判断一些简单函数的单调性。

能力目标：培养学生的分析、归纳和总结能力；培养学生运动变化和数形结合的数学思想；培养学生理论联系实际的辩证唯物主义思想。

情感目标：营造亲切、活跃的课堂气氛，实施多元化评价，激励学生，使学生尝试成功，以点燃学生的学习热情。

教学重点、难点

重点：函数单调性概念和函数单调性的判断。

难点：判断函数的单调性。

教学过程设计与分析

创设问题情境

多媒体：学校的简介。（利用Flash进行演示）

提出问题：学校准备建造一个长方形的花坛，面积设计为16平方米。由于周围环境的限制，其中一边的长度长不能超过10米，短不能少于4米，求花坛半周长的最小值和最大值。

教师说明：此环节为创设情境。我们学校是上海市投资新建的郊区四所寄宿制重点高中之一，有着一流的硬件设施，绿化建设正在进行之中。抓住这一点，我设计了这节课的引例，切合实际，让学生有种亲切感。提出问题后，让学生思考、讨论下列问题：如何把实际问题归结为数学问题？经过思考、讨论，估计学生可以把问题归结为：设受限制一边长为x米，4≤x≤10，则另一边为16/x米，求半周长y＝x＋16/x（4≤x≤10）的最小值和最大值。如何求最小值？——运用基本不等式。如何求最大值？经过思考、讨论，最后大家一致认为利用y＝x＋16/x（4≤x≤10）的图像可以得出结论。

多媒体：利用Flash演示y＝x＋16/x（4≤x≤10）的图像,如图1所示。

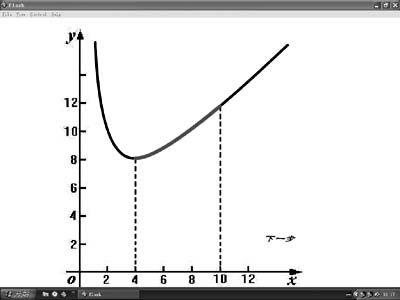
教师说明：利用Flash给出函数的图像，从函数图像可以直观地得出结论，但是缺乏理论依据。指出缺乏理论依据的结论是站不住脚的，所以问题转化为寻找其理论依据，从而引入课题。这样可以培养学生严谨的治学态度。

揭示课题，引入新课

1.几何画板演示，点明课题。

多媒体：利用几何画板演示y＝x＋16/x（4≤x≤10）的动态的变化过程。用鼠标从左向右缓慢拖动y＝x＋16/x（4≤x≤10）上的A点，引导学生观察A点的纵坐标的变化情况（随着自变量x的增大，函数值y也在增大），如图2所示。

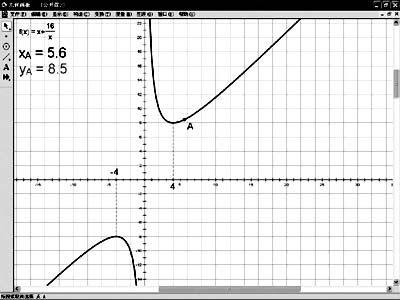
2.请学生根据自己的理解给出增函数定义。

一般地，对于给定区间上的函数f(x)：如果对于属于这个区间的自变量的任意两个值x₁和x₂，当x₁＜x₂时，都有f(x₁)＜f(x₂)，那么就说函数f(x)在这个区间上是增函数。

3.请学生通过类比得出减函数的定义。

教师说明：在减函数定义的教学过程中，我改变了以往“灌输结论”的做法，让学生通过对增函数定义的理解从而得到减函数的定义，培养了学生的类比的重要数学思想方法，对于学生学习新知识、新概念有很大的帮助。

巩固新知，深化扩展

1.一次函数的单调性问题。

[例1]证明函数f(x)＝3x＋2在区间(－∞，＋∞)上是增函数。

引申：探索一次函数f(x)＝kx＋b(k≠0)在区间(－∞，＋∞)上的单调性。

2.二次函数的单调性问题。

[例2]判断函数f(x)＝x₂－2x的单调区间，并加以证明。

教师说明：例题的给出由简单的一次函数到二次函数，遵循了学生一般的认知规律，使学生容易接受，易于理解。在二次函数f(x)＝x²－2x的单调性的证明中，分工合作，第一、二组的学生完成函数在[1，＋∞)上的证明；第三、四组的学生完成函数在(－∞，1]上的证明，倡导自主学习、合作学习的新的学习方式。通过例1、例2的解决，让学生归纳判断函数单调性的基本步骤，培养学生分析、归纳和总结的能力。

判断函数单调性的基本步骤：

第一步，设x₁、x₂是区间内的任意两个实数，且x₁＜x₂。

第二步，比较f(x₁)、f(x₂)的大小。

第三步，给出结论。

自主解决——[引例]的解决

教师说明：有了上述理论作基础，一开始提出的问题就能迎刃而解：证明函数y＝x＋16/x在区间[4，10]上是增函数；得出结论，当x=10时，y_max=11.6。此环节起到了首尾呼应的作用，让学生体会到数学源于生活又服务于生活，体会到数学的魅力，并指出，函数单调性的研究为解决函数的最值问题提供了又一重要方法，可见研究函数的单调性是非常有必要的。那么我们为何不乘胜追击，探索更一般的情况，研究函数y=x+k/x(k∈Ｒ)的单调性。

多媒体：利用Authorware进行探索、总结y=x+k/x(k∈Ｒ)图像，寻找一般的结果。（从特殊到一般）如图3、4所示。

学生总结、教师归纳

教师说明：提出问题，这节课你学到了哪些数学知识？学生一一罗列：函数单调性的概念、判断函数单调性的常用方法、证明函数单调性的基本步骤。进一步提出问题：整堂课体现了哪些重要的数学思维？自问自答：从特殊到一般的研究方法；从大胆的猜想到严格的证明；数形结合、类比的思想。利用计算机使我们探索数学问题的过程更加直观、简洁和生动。

（作者单位：上海市南汇中学 201300）

点评

“问题是数学的心脏”。一个好的问题能引起学生兴趣，启迪学生的思考，将思维引向深刻。闵丽红老师的“学校花坛问题”是一个很好的实际问题：在学校绿化建设中，如何建造其费用最省？闵老师通过引导学生观察问题、发现问题、提出问题、探究和解决问题，使学生感受到数学源于生活又服务于生活，以培养学生形成科学观，培养学生的创新精神和实践能力。

这节课最大的特点是贯穿始终的现代软件技术的应用，娴熟地运用了PowerPoint、Authorware、Flash和几何画板等多种教学媒体和手段，通过直观的画面和动态的影像，将数学知识的发生和发展淋漓尽致地展现在学生面前。尤其在利用Authorware进行探索、总结图像的过程中，首先，研究特殊情况（当k=2时）,使用列表描点、几何绘图两种方法，利用计算机动态地绘画出它的图像。紧接着，探索、总结其一般结果：随机地输入k的值，随即电脑显示相应函数的图像。最后，显示所有情况，一目了然，使每位学生对于图像都有了清晰的、精确的认识。利用多媒体处理这一部分达到的效果，是传统教学所不及的，充分地体现了现代技术的优越性。

现代建构主义的教学观认为，知识并不能简单地由老师传授给学生，而主要由每个学生依据自身已有知识和经验主动地加以建构。闵老师理解了这一观点的精髓，改变了以往单一被动的学习模式，提倡主动探索、合作学习，体现了上海市二期课改的精神，是一节成功的公开展示课。