快速生成海面目标雷达微多普勒特征的方法

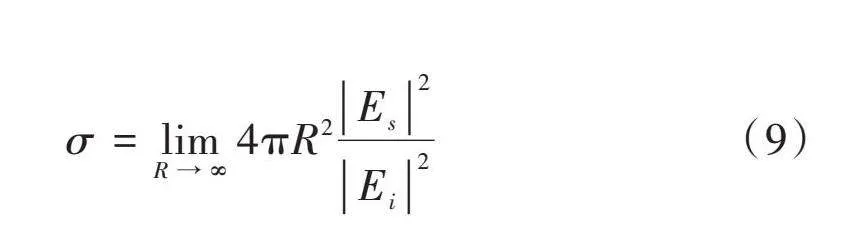
摘" 要： 由于海浪在不同海况下展现出的复杂性和多变性，海面场景下运动目标的雷达回波数据获取与模拟一直是研究的难点。针对角反射体和舰船这两个典型目标，文中创新性地提出了一种数学方法来解决这一问题。首先根据海面目标的耐波性理论，分析目标的六自由度运动，结合欧拉旋转矩阵建立动态运动模型；其次根据设定的雷达参数，使用FEKO电磁仿真软件获取静态时全方位俯仰角的雷达散射截面RCS；然后结合动态运动模型和静态散射数据建立数学模型；最后通过仿真实验可知：利用此模型可以精准、快速地获取海面运动目标的雷达回波数据，采用短时傅里叶变换处理数据可得到微多普勒特征，能够为基于微多普勒特征的海面目标分类算法提供样本支撑。

关键词： 海面目标； 微多普勒； 时频分析； 角反射器； 耐波性； FEKO

中图分类号： TN955⁃34" " " " " " " " " " " " " " 文献标识码： A" " " " " " " " " " " "文章编号： 1004⁃373X（2025）03⁃0007⁃06

A method for rapid generation of radar micro⁃Doppler features of sea surface targets

WANG Zheng1， 2， SUN Zhaoyang2， LI Shibao1， ZHOU Hang2， LI Lianghai3， LI Fazheng1， 2

（1. College of Oceanography and Space Informatics， China University of Petroleum （East China）， Qingdao 266580， China;

2. Beijing Research Institute of Telemetry， Beijing 100076， China;

3. China Aerospace Electronics Technology Research Institute， Beijing 100094， China）

Abstract： It is difficult to obtain and simulate the radar echo data of moving targets in the scene of sea because the waves have complex and variable shapes in different sea conditions. In view of this， a mathematical method is proposed innovatively by focusing on the two typical targets of corner reflectors and ships. According to the sea⁃keeping theory of the sea target， the six⁃degree⁃of⁃freedom motion of the target is analyzed and the dynamic motion model is established in combination with the Euler rotation matrix. According to the set radar parameters， the radar cross section （RCS） of static omni⁃directional attitude angle is obtained by the electromagnetic simulation software FEKO. Then the mathematical model is established by combining the dynamic motion model and static scattering data. It is known by the simulation experiment that the model can accurately and quickly obtain the radar echo data of sea moving targets， and then the data are processed by the short⁃time Fourier transform to obtain the micro⁃Doppler feature. To sum up， the model can provide sample support for the sea target classification algorithm based on the micro⁃Doppler features.

Keywords： sea surface target; micro⁃Doppler; time frequence analysis; corner reflector; sea⁃keeping ability; FEKO

0" 引" 言

海面目标的检测在军用和民用等领域具有广泛的应用和需求，比如角反射体具有便于存储使用、易携带、能快速布防形成雷达假目标等优点[1]，被当作无源干扰广泛应用，快速高效地区分角反射体和舰船是近些年的热门研究内容[2⁃3]。以海面拖曳式角反射体为例，假设其在海面上除了具有一定的平动速度，在随机海浪的作用下，还会产生绕物体中心的摇摆运动，这种运动属于微动的范畴[4]。微动广泛存在于各类事物中，例如直升机旋翼的旋转、汽车轮子的旋转、人体肢体的摆动等。不同的目标具有不同的散射现象和机理，微多普勒特征和目标结构特征之间存在联系[5]。目前在军用和民用等领域，微多普勒特征与特征融合、深度学习等方法结合，在目标分类任务中发挥了重要作用[6⁃7]。

在实现准确的目标分类和精确的电磁散射特性分析时，获取高置信度的目标数据是至关重要的一步。相比于目标实验测量[8]和微波暗室缩比测量[9]，建模仿真[10]具有低成本、易重复的优势，在实际测试之前先对目标进行分析，可以节约成本。针对海面目标的雷达回波仿真研究存在诸多挑战，这主要是由于海面环境的复杂性和动态性导致的，包括复杂的海况、海浪影响下的目标运动形式以及目标雷达散射截面（RCS）的变化等因素。

本文以角反射体和舰船为研究对象，旨在通过建立一个数学模型来快速、准确地获取具有微多普勒特征的雷达回波数据，可以真实反映海面目标的结构特性和运动状态。雷达回波仿真需要解决两个问题：目标受到海浪作用下的运动形式的仿真和目标在不同的雷达方位俯仰角下RCS的变化。

针对这两个问题，模型的建立分为两个步骤：

1） 动态运动模型的建立。推导目标的运动形式进而得到雷达中心相对目标中心的实时方位俯仰角。

2） 静态电磁散射数据库的建立。利用FEKO电磁仿真软件计算出目标全方位俯仰角的静态RCS。

最后通过仿真实验分析验证了通过该模型可快速为海面目标分类生成大量、准确，具有微多普勒特征的雷达回波数据。

1nbsp; 海面目标动态模型仿真原理

1.1" 海浪作用下的摇摆模型

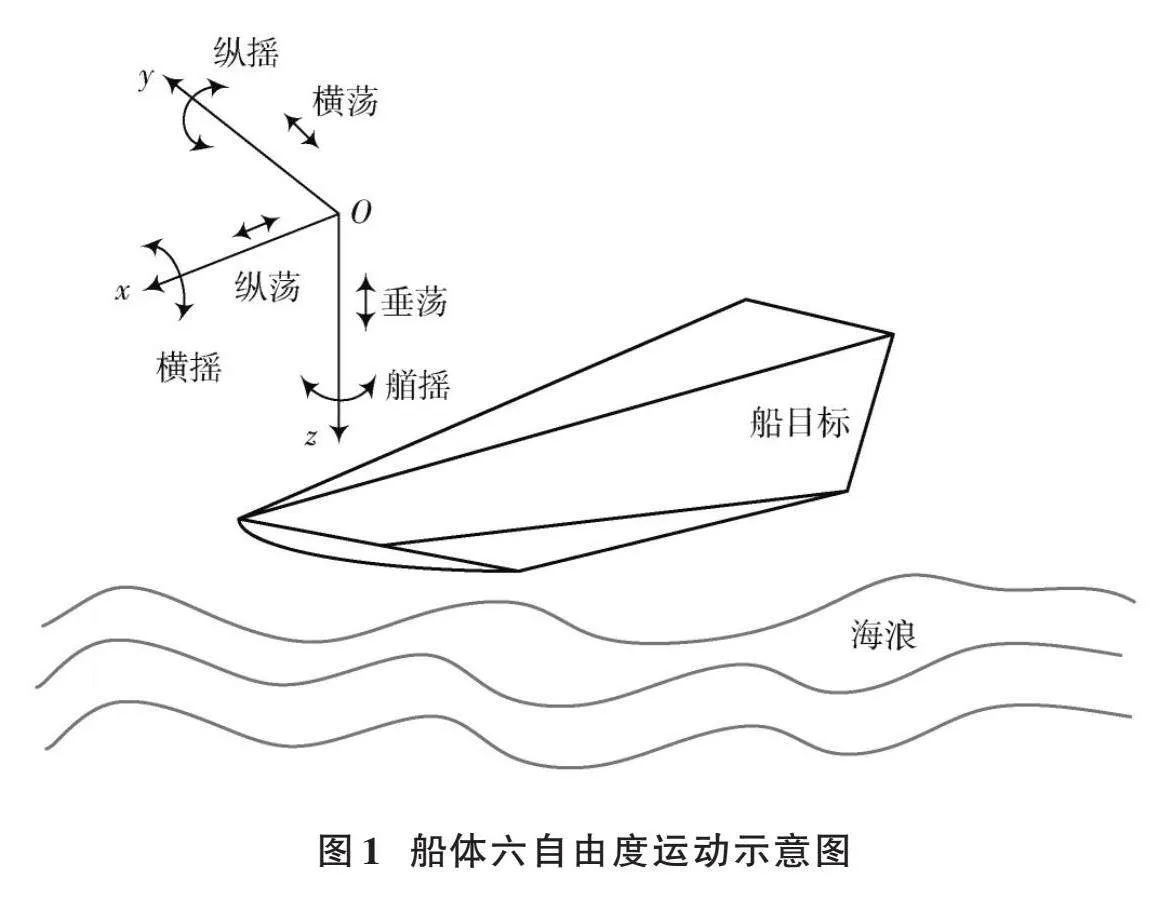
海面目标的运动是基于船舶的耐波性理论，这一课题被国内外学者进行了长期深入的研究和探索。海面目标在海浪中呈现了三种角位移运动：横摇、纵摇、艏摇；三种线位移运动：横荡、纵荡、垂荡。称为六自由度运动[11]。具体定义如图1所示，坐标系[xOy]固定在船体中，[O]点为船体的运动中心，[Ox]的正轴指向船首，[Oy]的正轴指向右舷方向，[Oz]的正轴垂直向下。

实际海况下的波浪具有复杂性和随机性，是由无限个不同幅度和频率的单元规则波线性叠加而成。当海面目标以航速[u]、航向角[χ]（船首与海浪传播方向之间的夹角）在海上航行时，参数如下[12]：

[Sφ（ωn）=0.78ω5nexp-3.11H2ω4nδn=Sφ（ωn）2Δωωe=ωn-ω2ngucosχSϕ（ωe）=Sφ（ωn）1-2ωngucosχ]" （1）

式中：[Sφ（ωn）]为国际船模试验池会议ITTC推荐的单参数标准海浪谱；[H]为有义波高，它表征了波高的统计值，不同的海况下，[H]的输入值是不同的，可以通过查表方法获取[13]；[ωn]为第[n]个单元规则波的角频率；[δn]表示第[n]个单元规则波的波高；[ωe]是遭遇频率，[Sϕ（ωe）]是遭遇海浪谱。遭遇频率和遭遇海浪谱定义为在海面目标坐标系下观测得到的海浪频率和海浪谱。

海面目标任意时刻的摇荡运动[12]表达式如下：

[θi（t）=n=1NRaoi（ωn）δncos（ωnt+ψn+ϕi，n） ] （2）

式中：[i]=1，2，3，4，5，6，表示六个自由度；[ψn]是在[0]～[2π]之间变化的随机相位；[Raoi]定义为目标在第[i]个自由度的幅值响应函数，描述了海面目标对各个频率单元规则波的响应程度；[ϕi，n]是幅值响应函数的相位；[Raoi]是幅值响应函数的幅度。[Raoi]和海面目标的尺寸、吃水深度、结构等有关，通过在正横规则波中求解线性微分方程的方法求解出幅值响应函数[Raoi] [13]，需要定义船体的长、宽、吃水深度、阻尼系数等固定参数。

在实际运动中海面目标具有一定的位移速度，会产生多普勒频移，所以在运动方向上的微动（横荡、纵荡）对整体多普勒的影响不大，海面目标的垂荡运动引入的径向距离变化率非常小，故而引入的多普勒频率分量较小。为了简化实验，海面目标微动情况只讨论摇摆情况，也就是横摇、纵摇、艏摇三种角位移运动。

将式（1）的参数计算代入式（2）中，得到函数[B]，输入的变量是由海况等级决定的，有义波高[H]，输出为海面目标的3个摇摆运动曲线[θi（t）]。

1.2" 实时方位俯仰角计算

目标在波浪中的运动是三维空间的复合运动，对于沿坐标轴旋转的纵摇、横摇、艏摇而言，三维转动其每一转角分量随时间的变化可以用一个函数表示，由函数[B]输出的[θi（t）]可以代替三个转角分量，表达式如下：

[φ=θ1（t），" θ=θ2（t），" ϕ=θ3（t）] （3）

[t]时刻的海面目标旋转矩阵表达式如下：

[Mrot（t）=A1（φ）⋅A2（θ）⋅A3（ϕ）] （4）

式中：[A1（φ）]、[A2（θ）]、[A3（ϕ）]分别为船体绕[x]、[y]、[z]轴的旋转矩阵[14]，表达式如下：

[A1（φ）=1000cosφ-sinφ0sinφcosφA2（θ）=cosθ0sinθ010-sinθ0cosθA3（ϕ）=cosϕ-sinϕ0sinϕcosϕ0001]" （5）

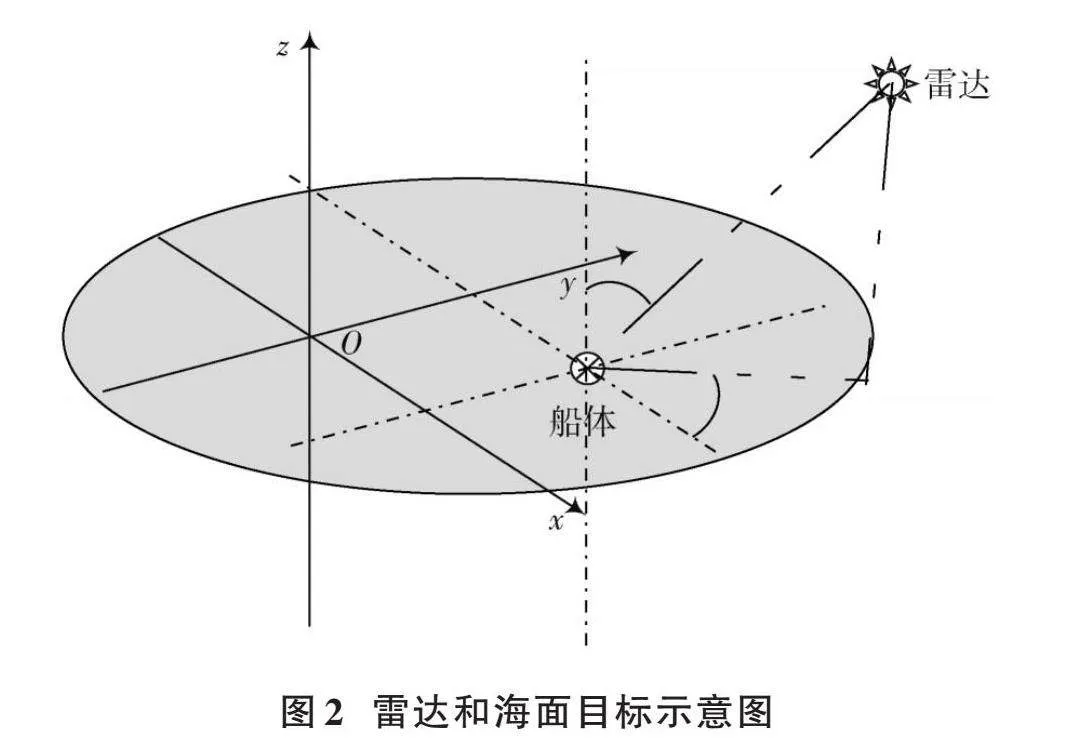
根据旋转矩阵求雷达相对于海面目标中心的方位俯仰角，设定地理坐标系，[xyz]为固定地理坐标系，雷达在地理坐标系中的位置为[（xm，ym， zm）]，海面目标在地理坐标系中的坐标为[（x0，y0， z0）]，目标在海面的航速为[u]，航向角为[χ]。雷达和海面目标的示意图如图2所示。在本场景的设定中海浪沿着[y]轴正方向运动，航向角就是船头的运动方向与[y]轴正方向的夹角。

在各慢时间采样时刻，雷达到目标中心的矢量坐标计算如下：

[xl（t）yl（t）zl（t）=Mrot（t）xmymzm-x0+utsinχy0+utcosχz0] （6）

目标转动时，雷达到目标中心的斜距表达式为：

[R（t）=xl（t）2+yl（t）2+zl（t）2] （7）

那么根据对应关系，各个慢时间[t]，雷达视线相对于目标中心的俯仰角[ψ（t）]和方位角[α（t）]的表达式如下：

[ψt=arccoszltRtαt=arctanyltxlt]" （8）

联立式（3）～式（8）可得到函数[E]，输入为雷达与目标的初始坐标和横摇、纵摇、艏摇三种自由度摇摆运动函数[θi（t）]，输出为雷达与海面目标中心的实时俯仰方位角[ψt]和[αt]。

2" 海面目标静态散射数据的计算

在雷达目标的回波仿真中，对不同目标选择不同的RCS计算方法很重要，不同的计算方法适用于不同的目标，和目标的电尺寸与材料介质有关[15]。

雷达后向散射截面积（RCS）的单位是[m2]，符号为[σ]，定义如下：

[σ=limR→∞4πR2Es2Ei2 ] （9）

式中：[R]是距离；[Es]是远场散射电场的强度；[Ei]是远场入射电场的强度。

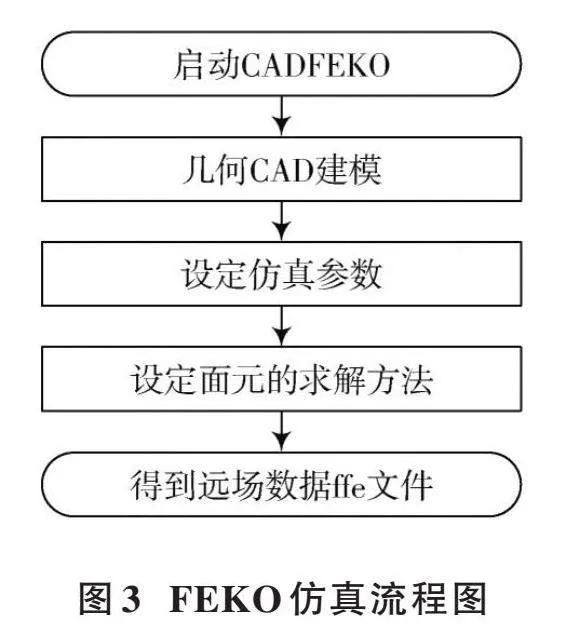
传统的RCS计算是目标和雷达相对位置固定，把目标看为由固定的散射点组成，计算目标的RCS。但是具体的场景下，海面目标具有特定的结构，当雷达中心和目标质心的俯仰角方位角发生变化时，RCS的幅度和相位都会发生变化，进而决定了微多普勒信息的变化，所以为了得到动态变化所影响的回波，就需要先对整个海面目标的静态全方位俯仰角下的RCS进行仿真计算。用物理光学法（PO）和大面元物理光学算法（LEPO）分别对角反射体和舰船进行仿真计算，可以提高计算效率，减少内存占用。

FEKO仿真流程图如图3所示。

3" 数学模型的建立

利用前期的推导和仿真分析得到静态散射数据和动态运动模型，由此建立一个数学模型[Z]，需要给定一个海面目标，设定输入参数，利用此数学模型即可快速生成此目标的雷达回波样本数据。数学模型[Z]的示意图如图4所示。

雷达发射的是载频为[f]的脉冲波，假设从一个散射点[P]返回的信号基带是距离[r（t）]的函数，表达式如下：

[s（t）=ρ（x，y， z）expj2πf2r（t）c=ρ（x，y， z）exp{jΦ[r（t）]}] （10）

式中：[ρ（x，y， z）]是在目标本地坐标系[（x，y， z）]中描述散射点[P]的反射率函数；[c]是电磁波的传播速度。

在某一时刻，[s（t）]的值是个复数，[data=a+bi]，所以在一段时间[t]的雷达回波数据是由复数组成的矩阵，[timedt]是维数，[time]是雷达观测时间，[dt]为时间间隔，是雷达的脉冲重复频率PRF的倒数。

静态回波数据由FEKO导出的ffe文件进行解析获取，依次读取在每个俯仰方位角的数据。

[data=ReEθ+ReEφ+ImEθ+ImEφi] （11）

式中：[ReEθ]和[ImEθ]是俯仰向的实部和虚部；[ReEφ]和[ImEφ]是方位向的实部和虚部。

如果要得到更小的角度间隔的数据，可采用线性插值法拟合，最终得到雷达回波[data]数据库[M]。

[data=M（φ，θ）] （12）

式中：[φ]是方位角；[θ]是俯仰角。

设定的函数[B]如下式：

[θi（t）=B（H）]" "（13）

式中：[H]代表有义波高；[i]=1，2，3，分别表示横摇、纵摇、艏摇三种摇摆运动。

设定的函数[Ε]如下：

[[ψ（t），α（t）]=Ε（rad，tar，θi（t））]" "（14）

式中：[rad=（xm，ym， zm）]表示雷达在地理坐标系中的初始位置坐标；[tar=（x0，y0，z0）]为海面目标中心点在地理坐标系中的初始位置坐标；[θi（t）]由函数[B]得出；[ψ（t）]和[α（t）]表示输出得到的俯仰角和方位角随时间的变化函数。

由式（12）～式（14）可得：

[Cdata=data[N]=M（φ，θ）[N]=M[ψ（t），α（t）][N]=M[E（rad，tar，θi（t））][N]=M[E（rad，tar，B（H））][N] ] （15）

式中：[N=time*PRF]，[time]是雷达观测时间，PRF是脉冲重复频率；[Cdata]是目标的雷达回波数据。

利用短时傅里叶变换（STFT）作时频分析提取微多普勒特征，其原理简单、计算效率高，属于线性变换。在工程应用上，STFT常采用离散形式[16]。

[S（m，n）=i=-∞+∞s（i）w（i-m）e-j2πni] （16）

式中：[s（i）]是离散雷达回波；[m]和[n]分别是时间和频率采样点；[w（i）]是窗函数。

将上述过程重复[G]次，就得到了[G]次样本数据。

综合上述计算流程将得到数学模型[Ζ]，定义如下：

[result=Ζ（time，rad，tar，H，G）] （17）

式中输入的变量依次是雷达观测时间、雷达初始坐标、海面目标初始坐标、海况等级、样本数量，输出为具有微动信息的雷达回波样本数据。

4" 仿真实验与分析

4.1" 实验准备

用FEKO对舰船、三角形角反、由4个三角形角反组成的组合角反进行CAD建模，计算RCS。

舰船参数：长为115 m，宽为14 m，甲板高度为5 m。三角形角反和组合角反的边长都设为5 m。俯仰角的范围是0～90°，方位角的范围是-90°～90°，角度间隔是0.1°，雷达入射波为单频3 GHz。三个海面目标的RCS如图5所示。单位为[dBm2]，从图5中可以看出RCS的复杂程度，舰船gt;组合角反gt;三角形角反，符合实际建模。

4.2" 模型性能分析

从两个方面来评判模型的性能：雷达回波仿真的精确度和雷达回波数据的可分性。为了简化实验，目标的速度和航向角设为固定值，速度为10 m/s，航向角为30°，雷达观测时间设为90 s，雷达的脉冲重复频率为90 Hz，海况等级为6级，查表得到有义波高[H]=3 m，设定雷达坐标为（30，40，50），随机生成三个目标舰船、三角角反、组合角反的初始坐标，分别为（60，70，0）、（-35，-50，0）、（30，-40，0），坐标的单位为m。分别用模型仿真和调用EDITFEKO仿真舰船、三角角反、组合角反的雷达回波数据，对雷达回波数据经过时频分析和信号处理得到时频图如图6所示。

经过图6a）和图6d）对比、图6b）和图6e）对比、图6c）和图6f）对比，由设定的条件可知，同一个海面目标的输入参数变量相同，由图像可知，数学模型仿真出的时频图与用EDITFEKO仿真出的时频图基本相同，验证了模型仿真出的雷达回波数据的准确性。在相同条件下，每次运行模型仿真出的时频图都有细微的差别，因为海浪的运动是随机且复杂的，可以反映较为真实的海面运动目标的微多普勒特征。

由图6a）、图6b）、图6c）对比可知，对于由模型仿真出的舰船、三角角反和组合角反的雷达回波数据，从时频图可以很容易分辨出三者的区别，三角形角反和组合角反的微多普勒频率的幅度大致相同，但是组合角反比三角形角反的微多普勒频率分量更多，这符合实际建模，因为组合角反比三角形角反的结构更加复杂。舰船的结构非常复杂，所以时频图的微多普勒频率分量呈现出极其不规则的形式，和两个角反形成鲜明的对比，通过肉眼可以直接进行分辨，数据的特征明显，作为训练集可以达到分类的效果。

4.3" 仿真时间对比

将数学模型仿真和通过EDITFEKO脚本顺序运行出的时频图消耗的时间进行统计。例如仿真一张时频图，8 192个脉冲回波，经过10次测试，消耗的平均时间如表1所示。

通过表1的比较得到结论，利用此模型生成雷达回波数据节省了大量的时间，达到了快速生成雷达回波样本数据的目的。

5" 结" 语

针对海面场景下运动目标雷达回波数据难以直接获取和有效模拟的问题，本文创新性地融合了船舶耐波性理论、欧拉旋转变换、FEKO电磁建模仿真技术以及微多普勒时频域分析等理论，构建了一个具备高度适用性和精确性的数学模型。

相较于文献[12]中对海面角反射体的微多普勒频率仿真研究，本文所提出的模型能够针对多种类型的海面目标进行仿真分析。通过该模型，可以快速、精确地生成包含微动信息的雷达回波数据，更真实地反映海面目标的结构特性和运动状态，为海面目标的分类训练提供了有力的数据支撑。

本文采用的将动态运动模型与静态散射数据相结合的建模方法具有广泛的适用性，这种方法可以进一步拓展到其他场景下的运动目标雷达回波数据模拟中，为相关领域的研究提供新的思路和方法。

注：本文通讯作者为王筝。

参考文献

[1] 张俊，胡生亮，杨庆，等.异型角反射体阵列寻优研究[J].海军工程大学学报，2019，31（6）：46⁃50.

[2] LÜ Q Z， FAN H X， ZHAO Y H， et al. Agile frequency RCS⁃based deep fusion network for ship and corner reflector identification [J]. IEEE geoscience and remote sensing letters， 2024， 21： 1⁃5.

[3] HE Y M， YANG H Z， HE H F， et al. A ship discrimination method based on high⁃frequency electromagnetic theory [J]. Remote sensing， 2022， 14（16）： 3893.

[4] CHEN V C. The micro⁃Doppler effect in radar [M]. Boston · London： Artech House， 2019.

[5] 李郝亮，陈思伟.海面角反射体电磁散射特性与雷达鉴别研究进展与展望[J].雷达学报，2023，12（4）：738⁃761.

[6] ABDU F J， ZHANG Y， DENG Z. Activity classification based on feature fusion of FMCW radar human motion micro⁃Doppler signatures [J]. IEEE sensors journal， 2022， 22（9）： 8648⁃8662.

[7] CHAKRABORTY M， KUMAWAT H C， DHAVALE S V. Application of DNN for radar micro⁃Doppler signature⁃based human suspicious activity recognition [J]. Pattern recognition letters， 2022， 162： 1⁃6.

[8] BEZERRA D X， LORENZZETTI J A， PAES R L. Marine environmental impact on CFAR ship detection as measured by wave age in SAR images [J]. Remote sensing， 2023， 15（13）： 3441.

[9] 骆颖.基于TDSBR的海上目标与角反射器复合时域电磁散射及干扰分析研究[D].西安：西安电子科技大学，2021.

[10] JIANG W Q， WANG L Y， LI X Z， et al. Simulation of a wideband radar echo of a target on a dynamic sea surface [J]. Remote sensing， 2021， 13（16）： 3186.

[11] 陈万紫，张培珍，黄健儿，等.动态海面上方船舶六自由度运动仿真[J].海洋技术学报，2019，38（1）：40⁃45.

[12] 黄孟俊，陈建军，赵宏钟，等.海面角反射器干扰微多普勒建模与仿真[J].系统工程与电子技术，2012，34（9）：1781⁃1787.

[13] 王广兴.基于响应幅值算子的船舶耐波性运动建模[D].大连：大连海事大学，2020.

[14] 吕方方.海面目标动态回波仿真与特性分析[D].西安：西安电子科技大学，2019.

[15] 张远浩.角反射器和舰船目标动态电磁散射特性研究[D].哈尔滨：哈尔滨工业大学，2022.

[16] 姚鑫.基于微多普勒特性分析的行人目标检测与识别方法[D].西安：西安电子科技大学，2022.