变频驱动游梁有杆泵系统仿真与频率优化研究

针对电机匀速驱动游梁抽油机运行过程中周期性交变载荷变化大、系统能耗高及故障多的问题，分析了电机变频驱动对抽油机运动规律、悬点载荷、变速箱扭矩及电机功率的影响，建立了变频控制抽油系统动态能耗的仿真模型。以电机输出功率均方根最小、输出功率峰值最小和负发电最小为目标函数，综合考虑平均频率不变、上下冲程时间分配、频率范围等约束条件，建立了周期运行频率优化设计的数学模型，并采用粒子群优化算法求解周期频率分布函数的傅里叶系数，即周期运行频率分布。实例分析表明：优化实时频率可以显著改善抽油机的动力性能，悬点载荷、曲柄扭矩和输出功率的峰值均有所降低；电机平均输出功率降低16.2%，负发电减少14.77%，节能效果显著。所得结果可为变频驱动游梁有杆泵系统的设计及应用提供参考。

游梁抽油机井；动态能耗仿真；频率分布；悬点；粒子群算法

TE28

A

DOI： 10.12473/CPM.202401076

Simulation and Frequency Optimization Research of Variable

Frequency Driven Beam Pump System

Zhang Chuanxin1" Yao Jinhang1" Kong Youwei2" Chu Haoyuan1" Tan Chaodong2，3" Feng Ziming4" Feng Gang5

（1.Research Institute of Engineering Technology， PetroChina Xinjiang Oilfield Company;2.College of Petroleum Engineering， China University of Petroleum （Beijing）;3.College of Information Science and Engineering， China University of Petroleum （Beijing）;4.School of Mechanical and Electrical Engineering，Wenzhou University;5.Xian Supcon World Technology Development Co.， Ltd.）

A beam pumping unit driven by a motor at a constant speed features greatly varying cyclic alternating load， high energy consumption and frequent failures during operation. In this paper， the motion behavior， load at the suspension point， gearbox torque and motor power of the pumping unit driven by a motor at variable frequency were investigated， and a simulation model for dynamic energy consumption of the variable frequency controlled pumping system was built. Taking the minimum root mean square of output power， minimum peak output power and minimum negative power generation of the motor as the objective functions， and considering the constraints such as constant average frequency， time share of up-down stroke and frequency range， a mathematical model for optimizing the cyclic operating frequency was built. In addition， the particle swarm optimization （PSO） algorithm was used to solve the Fourier coefficient of the cyclic frequency distribution function， that is， the cyclic operating frequency distribution. Case analysis shows that optimizing real-time frequency can significantly improve the power performance of the pumping unit. The peak values of polished rod load， crank torque and output power all reduce to some extent. The average output power of the motor decreases by 16.2%， and the negative power generation decreases by 14.77%， indicating a remarkable energy saving effect. The research results provide reference for the design and application of variable frequency driven beam pump systems.

beam pumping well;dynamic energy consumption simulation;frequency distribution;suspension point;PSO

基金项目：国家自然科学基金项目“基于大数据解析的大规模非集输油井群生产及拉运调度协同优化”（51974327）；国家自然科学基金项目“变速驱机-杆-泵全耦合动力学行为及优化运行节能机理研究”（51774091）；中国博士后科学基金项目“杆管液三维耦合振动力学行为及变速降载运行机制研究”（2018T110268）。

0" 引" 言

张传新，等：变频驱动游梁有杆泵系统仿真与频率优化研究

游梁式抽油机在匀速驱动时，由于其固有的结构特点，悬点和减速箱要承受剧烈的周期性交变载荷冲击。采用变频调速技术，使电动机转速与抽油机当前的负载相匹配，可以提高运行效率、节能降耗；但在变速驱动的应用过程中仍存在一些技术问题，如扭矩过大、过载和泵效率低。因此有必要对抽油机在变速驱动运行中的运动规律、能耗仿真、频率优化等开展进一步研究。

在抽油机能耗仿真方面，1963年，S.G. GIBBS［1］建立了抽油系统动态参数的一维波动方程模型，该力学模型可以用来描述杆柱纵向振动，实现了对抽油机悬点载荷的预测。1983年，D.R.DOTY等［2］考虑管筒内的液柱惯性和振动载荷对悬点载荷的影响，建立了杆柱-液柱的二维耦合波动方程，提高了悬点载荷的预测精度。1989年，余国安等［3］针对国内油管一般不锚定的现状，建立了杆柱-液柱-管柱三维耦合波动方程并提出求解方法。1990年，H.A.TRIPP等［4］对建立的耦合振动模型与试验进行了比较，证明了耦合振动模型的高精确性。1995年，S.D.L.LEKIA等［5］对单相不可压缩流体和单相可压缩流体分别建立数值仿真模型。1996年，董世民等［6-7］考虑到高转差电机的转子转速与磁场的不同步性，建立了考虑电机转速波动的有杆抽油机系统仿真模型。2015年，XING M.M.等［8］建立了皮带传动滑移模型，对采油系统进行生产优化，提高了计算精度和收敛速度。

抽油机变速优化运行最早由S.G.GIBBS在1975年提出［9］，并建立了变速运行时抽油机运动学和动力学的相关数学函数，以及给出求解耦合问题的流程。1990年，F.E.MCKEE［10］通过改变电动机输出电流的频率改变驱动速度，从而达到提高系统效率的目的。2009年，K.PALKA等［11］为了增加油井产量、减载节能，在单个抽汲周期内改变电动机转速。2016年，董世民等［12］建立了变频控制游梁式抽油机系统的仿真模型，以及实时频率优化设计模型，并采用了罚函数法求最优解。2017年，TAN C.D.等［13］建立了有杆抽油井的柔性变速控制模型及优化算法，通过采用遗传算法确定电机频率分布最佳傅里叶系数，实现产油量最大化。2018年，王林等［14］建立了抽油机变速运行动力模型并研究了机组动态特性的变化，降低了系统惯性扭矩峰值。2020年，宋微等［15］为充分利用抽油机运动部件的惯性能，建立了变速运动优化模型和求解方法，改善了抽油机井系统的综合性能。2020年，FENG Z.M.等［16］将抽油机运动方程、杆管液纵向耦合动力方程和电动机变速函数等联合成方程组，给出求解变速控制抽油机的求解流程，提出了变速运行对整个系统的综合性能评价方法。

抽油机变速运行技术是目前油田最先进的节能技术之一。目前大多数研究都展示了具体的变速优化曲线，但并没有具体说明速度曲线采用的优化方法，也没有明确数学模型［17］。本文综合考虑实时频率变化对抽油系统的影响，以输出功率均方根最小、输出功率峰值最小和负发电最小3个指标为优化目标函数，采用粒子群算法求解最佳频率分布。所得结果可为变频驱动游梁有杆泵系统的设计及应用提供参考。

1" 变频驱动游梁有杆泵动态仿真模型

游梁式抽油机主要由电动机、皮带轮、减速箱、四连杆机构、驴头、悬绳器、井口、组合杆柱、油管、抽油泵以及机架等部分构成。游梁式抽油系统如图1所示。

由图1可知，电动机的高转速通过皮带轮、减速箱传递递减，同时四连杆机构将旋转运动转换为光杆的往复运动，再通过抽油杆柱将原油举升到地面。变频控制的抽油机在运行过程中，通过变频器改变电机电源频率，从而改变电机转速，使得悬点运动速度发生变化，造成悬点动载荷和抽油机各构件的惯性扭矩发生变化，引起曲柄扭矩和电机功率需求变化。

因此，通过改变电源频率寻找合适的电机频率分布，有利于平衡抽油机负载、减少周期性交变载荷冲击、降低峰值扭矩和峰值功率，提高系统运行效率。这里通过图2所示的技术路线实现变频驱动抽油机井周期频率的优化。首先分析游梁式抽油机的运动规律，得到变频控制抽油机的电机频率分布和悬点载荷、悬点速度与加速度、曲柄轴净扭矩和输出功率等之间的关系，建立抽油井能耗动态仿真模型；然后将电机频率函数通过傅里叶级数展开，并采用粒子群优化算法求解最佳频率分布。

variable frequency driven beam pumping well

1.1" 悬点运动规律

抽油机结构和尺寸决定了抽油机的悬点位移［18］，抽油机悬点位移S如下：

S=±A（ψmax-ψ）（1）

式中：A为抽油机前臂长，m；ψ为后臂和基杆间的夹角，（°）；ψmax为抽油机下死点时ψ角最大值，（°）。

悬点速度和曲柄转角随时间的变化速度有关，悬点速度v的计算如下：

δ=ψmax－ψ（2）

v=Aωdδdθ（3）

式中：δ为游梁摆动角位移，（°）；ω为曲柄角速度，rad/s；θ为曲柄转角，（°）。

悬点加速度a计算如下：

a=AKRCLdω2

±sin β cos α sin ψ－RCsin α cos β sin θksin3 β

+TfAωdωdθ（4）

式中：K为基杆长度，m；R为曲柄半径，m；C为游梁后臂长度，m；Ld为连杆长度，m；α为曲柄与连杆间夹角，（°）；β为传动角，（°）；θk为曲柄与基杆间夹角，（°）；Tf为扭矩因数，m。

1.2" 悬点示功图计算

抽油机悬点载荷是研究地面装置受力状况的主要依据，悬点载荷主要由静载荷、惯性载荷和摩擦载荷组成。

抽油机上冲程悬点载荷为：

Fup=frLρrg+（fp－fr）Lρlg－fphcρlg+

frLρra+（fp－fr）Lρlaε+Fv+Ff（5）

式中：Fup为上冲程悬点载荷，kN；fr为抽油杆柱截面积，m2；L为抽油杆柱长度，m；ρr为抽油杆柱密度，kg/m3；g为重力加速度，m/s2；fp为活塞截面积，m2；hc为泵的沉没度，m；ρl为液体密度，kg/m3；ε为考虑油管过流断面扩大引起液柱加速度降低的系数，无量纲；Fv为振动载荷，kN；Ff为摩擦载荷，kN。

抽油机下冲程悬点载荷为：

Fdown=frL（ρr－ρl）g－frLρra－Fv－Ff（6）

式中：Fdown为下冲程悬点载荷，kN。

1.3" 抽油机扭矩计算

抽油机在变速运行情况下，曲柄变角速度转动会产生惯性扭矩，曲柄轴净扭矩为载荷扭矩、平衡扭矩与曲柄轴惯性扭矩之和：

Mn=ηk1cW－B+JbfrεbTf－Mcsinθ+τ+Jp3Rεq（7）

式中：Mn为曲柄轴净扭矩，kN·m；kl为指数，Tf＞0时kl=-1，Tf＜0时kl=1；W为悬点载荷，kN；B为不平衡重，kN；Jb为游梁转动惯量，kg·m2； εb为游梁摆动角加速度，m/s2 ；Mc为曲柄最大平衡扭矩，kN·m；τ为偏置角，（°）；ηc为四连杆机构的传动效率，无量纲；Jp3为曲柄转动惯量，kg·m2 ；εq为曲柄加速度，m/s2。

1.4" 电机功率计算

电机输出扭矩为：

Td=Mn+1DJp－Jp3εqiηk2m（8）

式中：Td为电机输出扭矩，kN·m；D为电机转子半径，m；Jp为电机转动惯量，kg·m2；i为传动比，无量纲；ηm为电机传动效率；k2为指数，Mn＞0时k2=-1，Mn＜0时k2=1。

电机转速为：

n=60f（t）p（9）

式中：n为电动机输出轴转速， r/min；t为时间，s；f（t）为变频器输出电压的瞬时频率，Hz；p为电动机极对数，无量纲。

输出功率P为：

P=Tdn9 550（10）

通过上述公式，可以计算出抽油机地面系统各节点的变量：悬点载荷、悬点速度与加速度、曲柄轴净扭矩，电机轴的扭矩、转速和输出功率等。因此可以基于上述公式对抽油机变频优化效果进行评价。

2" 基于粒子群周期运行频率优化求解

游梁式抽油机采用变频控制电机驱动时，电机转速和其他各节点的能耗参数都会发生改变。这里以电机的输出功率为优化目标建立实时频率分布优化模型，对实时频率函数进行傅里叶变换，并以其傅里叶系数为优化变量，采用粒子群算法优化求解实时频率分布。

2.1" 周期频率函数分布

对于游梁式抽油机变频调控，采用的基本原则是“重载慢驱，轻载快行”。1个运行周期内，在上冲程和下冲程的功率及载荷峰值点，减小电机频率，其他地方适当增大电机频率，保持平均频率不变，重新改变电机的频率分布。以此来减少周期性载荷的冲击，达到降载节能的目的。

图3为按照变频调控的基本原则，在平均频率50 Hz下常见的4种不同频率分布。图4为对应的电机输出功率对比。由图3和图4中可以看出，对于不同的频率分布，电机输出功率差异明显。因此通过优化周期频率分布，能够更好地降低能耗。

电机频率分布函数是以曲柄转角θ为自变量，2π为周期的连续函数，因此可以将电机频率用傅里叶级数展开，电机频率的分布曲线形态取决于傅里叶系数。傅里叶级数展开如下：

fθ=a0+∑Nm=1amcos（mθ）+bmsin（mθ）（11）

式中：fθ为曲柄转角为θ时的电机频率，Hz；a0、am、bm为傅里叶系数，Hz；N为傅里叶级数的截断项数，无量纲。

2.2" 周期频率优化方法

在抽油机变频优化调控中，考虑到实际应用时不同需求有不同的优化目标。这里综合选取输出功率均方根最小、输出功率峰值最小和负发电最小3个指标，作为游梁式抽油机系统的优化目标。

输出功率均方根最小评价函数为：

Y1=min" 12π∫2π0P2dθ（12）

输出功率峰值最小评价函数为：

Y2=minPmax（13）

式中：Pmax为最大输出功率，kW。

负发电最小评价函数为：

Y3=min∑Nθi=1min（0，Pi）（14）

式中：Pi为i点的输出功率，kW；Nθ为曲柄转角的位置，取1°，2°，3°，…，360°。

综合考虑输出功率均方根最小、输出功率峰值最小和负发电最小3个指标作为评价标准，并使用线性加权的方法构造数学模型，数学表达式为：

Y=ω1Y1+ω2Y2+ω3Y3（15）

式中：ω1、ω2、ω3分别为3个评价指标的权重系数，无量纲。

为了精确建立变频控制抽油系统动态能耗的仿真模型，需综合以下约束条件：

（1）电机转速不超过额定转速，n≤ne。

（2）减速箱输出轴扭矩不超过额定扭矩，Mnh≤Me。

（3）变速优化前后电机的平均频率不变，f—=f—0。

（4）上下冲程时间分配条件：0.9≤tu/td≤1.1。

其中：ne为电机额定转速，r/min；Mnh为减速箱输出轴扭矩，kN·m；Me为额定扭矩，kN·m；f—和f—0为变速前后电机的平均频率，Hz；tu和td为上、下冲程时间，s。

2.3" 基于粒子群算法的频率分布优化

粒子群算法（PSO）通过模拟个体间信息的交流和合作优化问题，粒子通过不断改变自身的速度和位置实现寻找最佳目标。该算法具有并行处理、鲁棒性好等特点，能以较大概率找到问题的全局最优解，且计算效率比传统随机方法高，其最大的优势在于简单易实现、收敛速度快。将其应用到抽油机电机变频优化中，主要步骤如下。

（1）生成粒子群。将电机频率通过三阶傅里叶展开，将傅里叶系数a0、a1、b1、a2、b2、a3、b3作为一组初始解。

（2）计算适应值。根据输入的傅里叶系数和游梁式抽油机地面能耗动态仿真模型，计算目标函数作为适应值。

（3）通过迭代，更新每个粒子的速度和位置，粒子的速度和位置计算如下：

vT+1i=λ·vTi+c1·r1·bi－xTi+

c2·r2·gi－xTi（16）

xT+1i=xTi+vT+1i（17）

式中：λ为惯性权重；T为粒子迭代次数；vTi为粒子速度；xTi为粒子位置；c1、c2为学习因子；r1、r2为加速因子；bi和gi分别为粒子历史最优值和当前最优值；式中各量均无量纲。

（4）评估粒子的适应值。计算目标函数，更新粒子当前最优位置和全局最优位置。

（5）判断是否满足输出条件，如果满足，输出最佳傅里叶系数；如果不满足，返回步骤（3），直到满足结束条件。

采用粒子群算法优化频率分布主要有以下优点：①可同时对傅里叶系数a0、am、bm进行调整，相比人工逐个调试各项参数的方法效率更高；②可以对大量参数的结果自动进行计算，寻优范围更广，优化度更高；③可以根据实际需求自定义目标函数；④可以对过程参数和目标结果范围进行约束，保障系统运行的稳定性。

采用粒子群优化算法求解周期频率分布函数的傅里叶系数算法流程图如图5所示。

3" 实例分析

3.1" 抽油机井能耗仿真计算

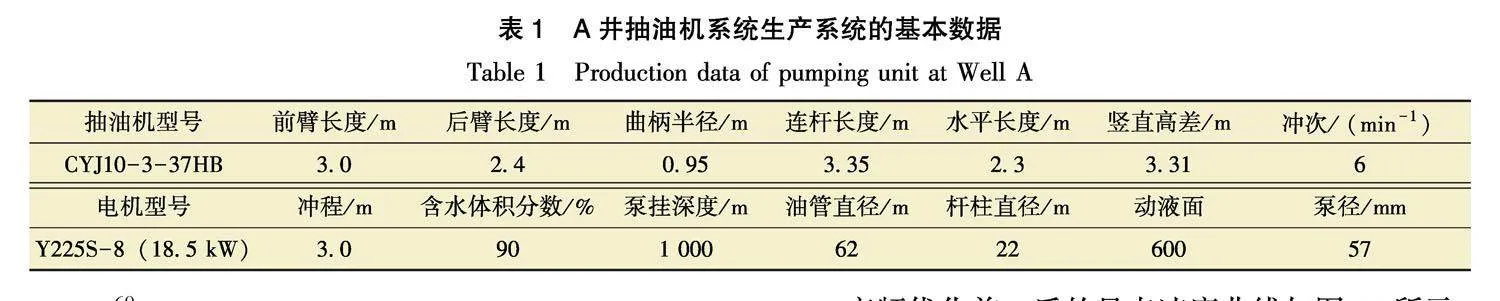
为验证模型和算法的适用性，以新疆某油田A井为例进行了分析评价。表1为A井抽油机举升系统基本生产参数。

根据游梁式抽油机地面能耗动态仿真模型对A井示功图、扭矩图、功率图仿真计算。图6为实测抽油机示功图和仿真结果，图7为实测曲柄轴净扭矩曲线与仿真结果，图8为实测电动机输出功率曲线与仿真结果。由图6～图8可以看出，仿真结果与实测曲线十分接近，表明该模型具有较高的仿真精度。

3.2" 变频优化效果分析评价

根据优化目标，采用粒子群算法进行优化，设置最大迭代次数为200，惯性权重为0.7，学习因子为0.6。图9为粒子群算法迭代过程中的适应度值变化图。由图9可以看出，迭代次数到130时，适应值函数下降趋于稳定，粒子群算法优化结果达到最优。最优傅里叶系数a0为50、a1为-6、b1为-4、a2为19、b2为-1、a3为4、b3为-2，优化后的最佳电机频率分布曲线如图10所示。

变频优化前、后的悬点速度曲线如图11所示。由图11可以看出，变频优化后悬点曲线的峰值速度有所降低，悬点速度峰值点后移，从而降低了因速度引起的动载荷、降低了峰值载荷。

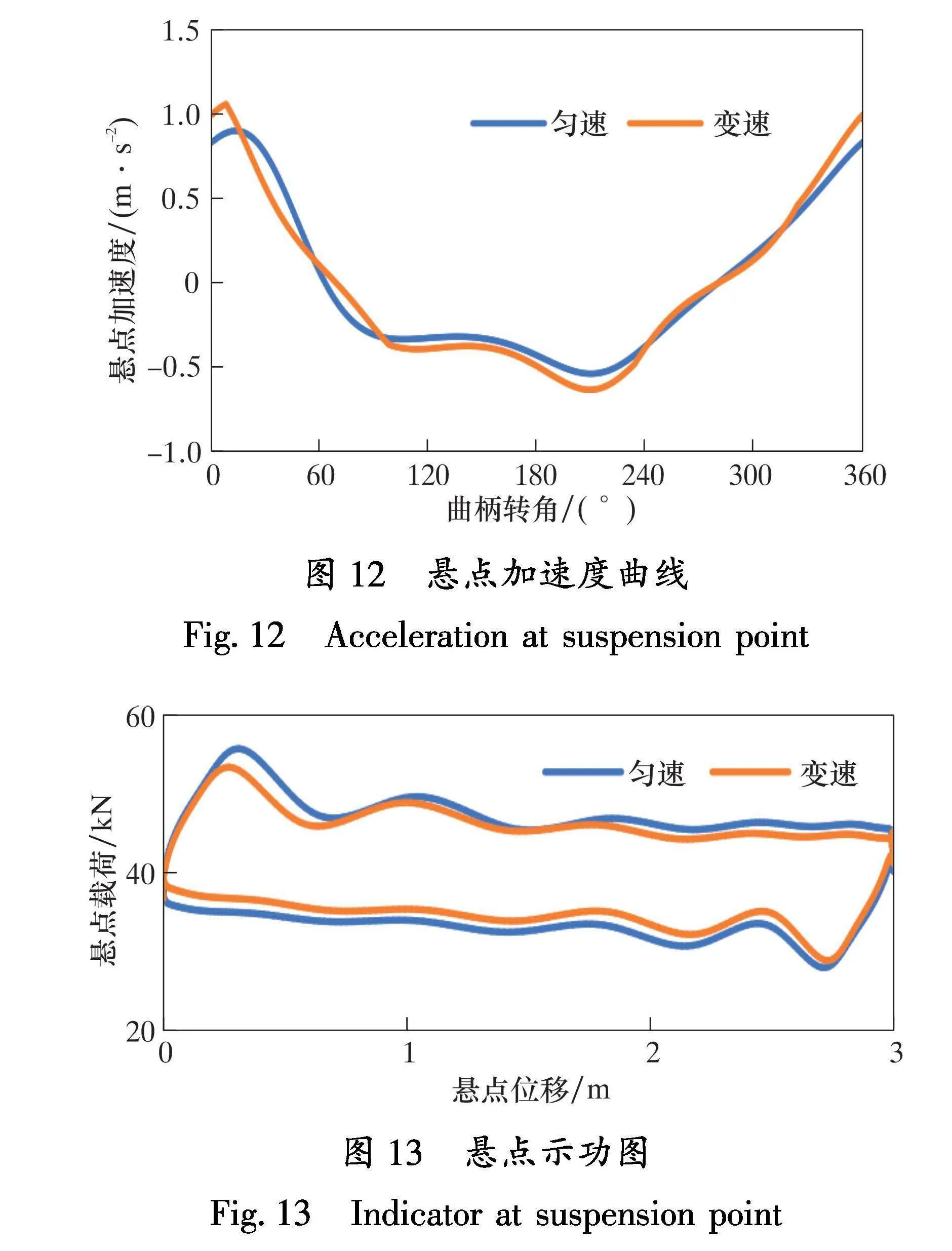
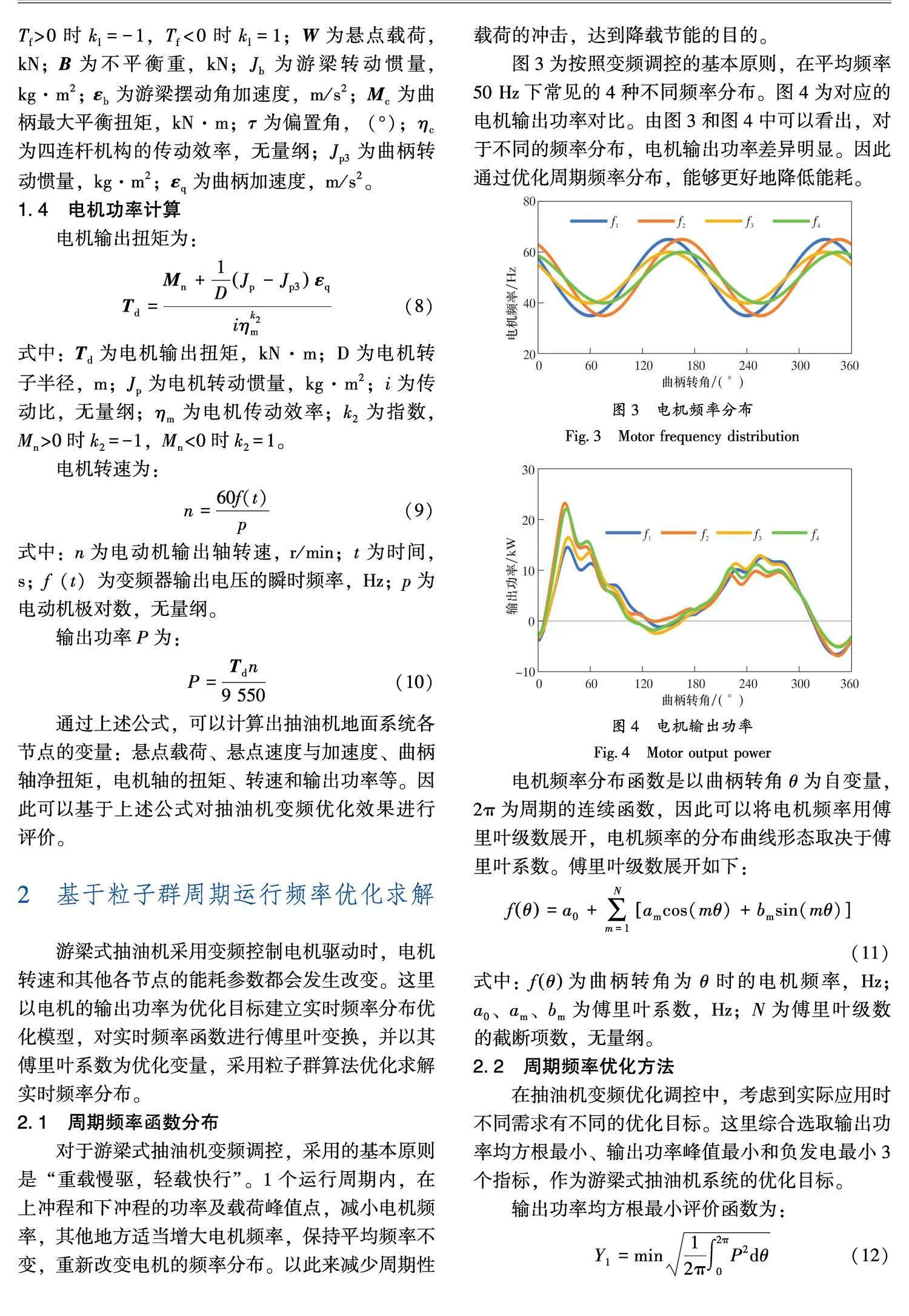
变频优化前、后的悬点加速度曲线如图12所示。由图12可以看出，变速运行时的悬点加速度峰值增加，将增加下冲程的惯性载荷，从而降低了下冲程的悬点载荷。变频优化前、后的悬点示功图如图13所示。由图13可以看出，变速驱动降低了悬点峰值载荷，也提高了悬点最小载荷，且悬点载荷波动减小，说明其有效缓解了悬点载荷冲击造成的影响。

变频优化前、后的减速箱输出净扭矩如图14所示。由图14可以看出：相比于匀速驱动，变速驱动下的减速箱输出净扭矩峰值有所降低，曲线中间部分扭矩几乎消除，优化效果明显；扭矩曲线更加平缓，扭矩波动小，使系统运行更加平稳。变频优化前后的电机输出功率如图15所示。由图15可以看出：变速驱动无论是功率峰值还是负功率都要降低很多，上、下冲程功率峰值相近，功率波动小；系统运行更加平稳，提高了电机效率。

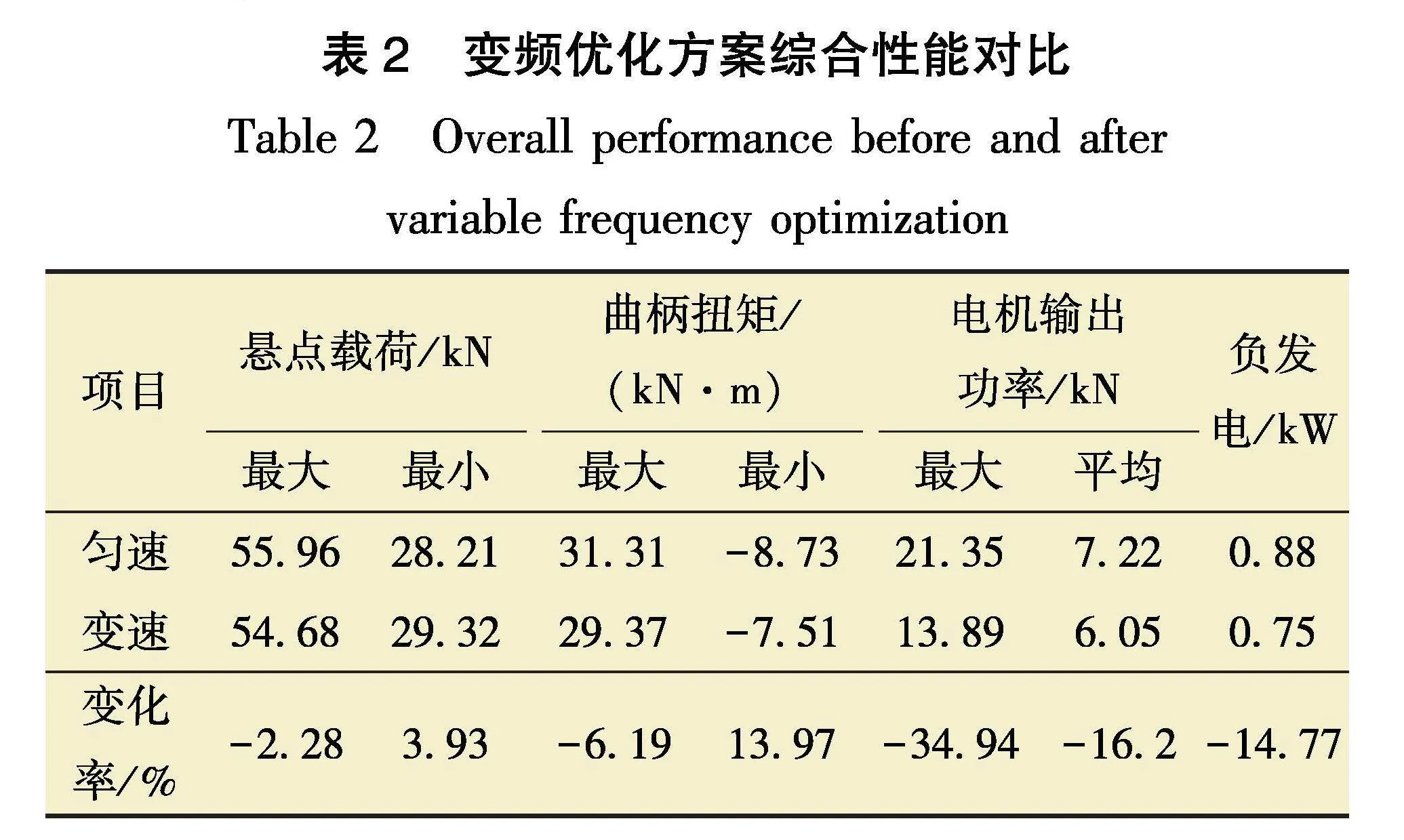
表2为变频优化前、后的综合性能对比。由表2可知：变频优化后，悬点载荷、曲柄扭矩和输出功率的峰值均有所降低，其中电机平均输出功率降低16.20%，负发电减小14.77%；提高了系统的稳定性，节电效果显著，改善了有杆抽油系统的动力性能。

4" 结" 论

（1）建立的变频驱动抽油机井能耗仿真模型和周期运行频率分布优化模型，可以作为游梁抽油机井能耗评价和节能设计的技术基础。

（2）建立的变频驱动游梁式抽油机能耗动态仿真模型，可以表征抽油机悬点载荷、减速箱扭矩及电机功率等能耗指标和运行频率的关系。

（3）基于傅里叶级数展开的抽油机实时频率优化模型和粒子群求解方法，可以快速准确地确定周期频率的最佳分布。

（4）现场验证结果表明，构建的能耗仿真模型与周期运行频率优化设计方法，改善了游梁有杆泵抽油系统的动力性能，节能效果显著，其中电机平均输出功率降低了16.2%，负发电减少了14.77%，节能效果显著。

［1］" "GIBBS S G. Predicting the behavior of Sucker-Rod pumping systems［J］. Journal of Petroleum Technology， 1963， 15（7）： 769-778.

［2］" DOTY D R， SCHMIDT Z. An improved model for sucker rod pumping［J］. Society of Petroleum Engineers Journal， 1983， 23（1）： 33-41.

［3］" 余国安，邬亦炯，王国源．有杆泵抽油井的三维振动［J］．石油学报，1989（2）：76-83．

YU G A， WU Y J， WANG G Y. Three dimensional vibration in a sucker rod beam pumping system［J］. Acta Petrolei Sinica， 1989（2）： 76-83.

［4］" TRIPP H A， KILGORE J J. A comparision between predicted and measured walking beam pump parameters［C］∥the SPE Annual Technical Conference and Exhibition. New Orleans， Louisiana： SPE， 1990： SPE 20671-MS.

［5］" LEKIA S D L， EVANS R D. A coupled rod and fluid dynamic model for predicting the behavior of sucker-rod pumping systems［J］. SPE， 1995， 10（1）： 26-33.

［6］" 董世民，崔振华，马德坤．电动机转速波动的有杆抽油系统预测技术［J］．石油学报，1996，17（2）：138-146．

DONG S M， CUI Z H， MA D K. Prediction of the behavior of sucker rod pumping system by taking account of the variation of motor rotating speed［J］. Acta Petrolei Sinica， 1996， 17（2）： 138-146.

［7］" 董世民，马德坤．有杆抽油系统动态特性的计算机仿真［J］．实验力学，1996，11（3）：277-284．

DONG S M， MA D K. Computerized simulation of dynamic behavior of rod pumping system［J］. Journal of Experimental Mechanics， 1996， 11（3）： 277-284.

［8］" XING M M， DONG S M. A new simulation model for a beam-pumping system applied in energy saving and resource-consumption reduction［J］. SPE Production amp; Operations， 2015， 30（2）： 130-140.

［9］" GIBBS S G. Computing gearbox torque and motor loading for beam pumping units with consideration of inertia effects［J］. Journal of Petroleum Technology， 1975， 27（9）： 1153-1159.

［10］" "MCKEE F E. Method and apparatus for controlling a well pumping unit： 07/043913［P］. 1990-11-27.

［11］" PALKA K， CZYZ J A. Optimizing downhole fluid production of sucker-rod pumps with variable motor speed［C］∥the SPE Western Regional and Pacific Section AAPG Joint Meeting. Bakersfield， California： SPE， 2009： SPE 113186-MS.

［12］" 董世民，李伟成，赵晓芳，等．变频游梁式抽油系统动态仿真与实时频率优化［J］．中国机械工程，2016，27（12）：1585-1590．

DONG S M， LI W C， ZHAO X F， et al. Frequency conversion beam pumping system dynamic simulation and real time frequency optimization［J］. China Mechanical Engineering， 2016， 27（12）： 1585-1590.

［13］" TAN C D，TAN P F，LI X L， et al. Research on flexible variable-speed control model and optimization method of rod pumping well based on genetic algorithm［C］∥2017 International Conference on Applied System Innovation （ICASI）. Sapporo， Japan： IEEE， 2017： 1771-1774.

［14］" 王林，师国臣，常瑞清，等．游梁式抽油机变速运行系统动态特性分析［J］．大庆石油地质与开发，2018，37（2）：96-101．

WANG L， SHI G C， CHANG R Q， et al. Analysis on the dynamic performances of the variable speed operating system for the beam pumper［J］. Petroleum Geology amp; Oilfield Development in Daqing， 2018， 37（2）： 96-101.

［15］" 宋微，冯子明，张德实，等．游梁式抽油机变速驱动优化建模与节能机理研究［J］．化工机械，2020，47（3）：348-354．

SONG W， FENG Z M， ZHANG D S， et al. Optimal modeling and research on energy-saving mechanism of beam-pumping units variable speed drive［J］. Chemical Engineering amp; Machinery， 2020， 47（3）： 348-354.

［16］" FENG Z M， GUO C H， ZHANG D S， et al. Variable speed drive optimization model and analysis of comprehensive performance of beam pumping unit［J］. Journal of Petroleum Science and Engineering， 2020， 191： 107155.

［17］" TAN C D， FENG Z M，LIU X L. Review of variable speed drive technology in beam pumping units for energy-saving［J］. Energy Reports， 2020， 6： 2676-2688.

［18］" 王常斌，陈涛平，郑俊德．游梁式抽油机运动参数的精确解［J］．石油学报，1998（2）：118-121， 10．

WANG C B， CHEN T P， ZHENG J D. An exact solution of kinematic parameters in beam pumping units［J］. Acta Petrolei Sinica， 1998（2）： 118-121， 10.

第一张传新，生于1968年，正高级工程师，1988年毕业于西南石油大学石油地质专业，现从事油气田开发相关技术研究工作。地址：（834000）新疆克拉玛依市。电话：（0990）6883776。email： zcxin@petrochina.com.cn。

通信作者：檀朝东，教授。email： tanchaodong@cup.edu。

2024-01-29" 修改稿收到日期：2024-08-28

任武