基于SPH法的套管冲蚀特性及结构优化研究

针对固井滑套压裂中冲蚀特性及结构优化等问题，基于光滑粒子动力学方法（SPH）建立球形砂粒冲击金属表面的SPH数值模型，模拟多个砂粒冲击套管材料42CrMo的微观过程，分析砂粒的撞击行为与冲蚀之间的关系；同时利用CFD模拟方法与Oka冲蚀模型结合现场实际工况，对不同端口特性的套管内壁进行冲蚀磨损的数值计算。研究结果表明：SPH法能较好地表现出砂粒在撞击套管材料时的微观变形，有助于研究微观下材料的变形影响因素，且由SPH法模拟得到的无量纲冲蚀速率随冲击角度变化的模拟数据与Oka冲蚀公式中冲击角函数趋势相符。端口特性参数对套管内壁的冲蚀有着较大的影响，具体表现在：随着端口数量、端口面积的增加，平均冲蚀速率均有一定程度的减小，但存在着边际递减效应；在研究的4种端口形状中，胶囊形端口的平均冲蚀速率最小。研究结果可为套管端口优化设计提供参考。

水力压裂；光滑粒子流体动力学；微观冲击模型；套管冲蚀；端口特性参数

TE28

A

DOI： 10.12473/CPM.202401006

SPH-Based Research on Erosion Characteristics

and Structural Optimization of Casing

Zhang Lei" Wang Chenrui

（College of Mechanical and Transportation Engineering， China University of Petroleum （Beijing））

For purpose of erosion characteristic research and structural optimization in cementing sliding sleeve fracturing， based on smoothed particle hydrodynamics （SPH）， a SPH numerical model of spherical sand particle impacting metal surface was built. The micro process of multiple sand particles impacting casing material 42CrMo was simulated， and the relationship between sand particle impact behavior and erosion was analyzed. Meanwhile， combined with field conditions， the computational fluid dynamics （CFD） simulation method and the Oka erosion model were used for numerical calculation on the erosion wear of casing inwall with different port characteristics. The research results show that the SPH method can effectively reflect the microscopic deformation of sand particles when impacting casing materials， which is helpful for studying the factors affecting material deformation at the microscopic level. The simulation data of variation of dimensionless erosion rate with impact angle obtained by SPH method is consistent with the trend of impact angle function in the Oka erosion formula. The port characteristic parameters have a great influence on the erosion of casing inwall. As the number and area of ports increase， the average erosion rate decreases to some extent， but there is a marginal decline effect. Among the four port shapes studied， the capsule shaped port has the lowest average erosion rate. The research results provide references for the optimum design of casing port.

hydraulic fracturing;smooth particle hydrodynamics;micro impact model;casing erosion;port characteristic parameters

基金项目：中国石油天然气股份有限公司科研项目“可开关固井滑套压裂起裂机理及结构优化研究”（21GJ-FW-010）。

0" 引" 言

张磊，等：基于SPH法的套管冲蚀特性及结构优化研究

固井滑套压裂技术是当前的主流水平井压裂技术，相较于其他压裂技术有着高效率、低成本等经济技术优势［1］。在固井滑套压裂过程中，含有砂粒或其他支撑剂的压裂液在流动时会对套管端口及端口周围内壁产生不同程度的冲蚀损伤。合理的套管端口结构设计可以改变端口附近流场，减轻含砂压裂液对端口及其周围的冲蚀磨损，达到安全压裂以及预防相关部件失效的目的。冲蚀是指材料受到微小而松散的流动颗粒冲击造成表面破坏的磨损现象，广泛存在于石油、机械等各个领域［2］。利用光滑粒子动力学（Smoothed Particle Hydro-dynamics， SPH）方法可以对材料在微观尺度上的撞击特性进行研究。

国内外学者对冲蚀机理与压裂工具优化进行大量研究。多数学者指出［3-5］，管壁冲蚀的重要因素是高速颗粒撞击，并利用数值模拟验证了当部件几何形状、材料物性一定时，冲蚀速率取决于颗粒撞击的速度、冲击角分布等因素。王川等［6］总结了造成滑套冲蚀中流场与颗粒的运动特点。魏辽等［7］通过试验与数值模拟得到了冲蚀量与砂比和排量之间的关系。WONG C.Y.等［8］对带有中心孔的平板进行冲蚀试验，研究石英砂粒对孔边缘的冲蚀现象，结果表明，复杂的几何模型对冲蚀结果会有影响。XU Y.Q.、向正新等［9-10］对井下工具进行研究，结果表明，可以利用CFD计算其内部流场分布并对井下工具进行结构优化。M.PARSI等［11］提出在冲蚀过程中存在挤压、切削等多种机制。DONG X.W.等［12-13］与M.TAKAFFOLI等［14］验证SPH方法在单颗粒撞击目标材料中的应用，其模拟结果与试验结果较为符合，验证了SPH法在模拟大形变中的优势。M.AZIMIAN等［15］与V.HADAVI等［16］利用FEM法与SPH法分别对角粒子冲击机理进行研究，结果表明，冲击粒子带有尖角时，会强化冲蚀作用，且冲蚀作用与冲击角与方位角均有关联。廖翔云等［17］通过SPH方法建立数值模型，研究了组合射流对岩石的冲蚀效果。王方祥等［18］基于SPH与有限元的耦合方法，模拟了压裂液返排期间放喷油嘴的磨损过程。

本文在上述研究的基础上，将SPH方法与CFD计算工作相结合，考虑端口特性参数，围绕固井滑套压裂过程中的套管冲蚀现象开展数值计算，通过SPH法模拟颗粒以不同角度多次撞击套管材料，验证套管材料42CrMo钢的冲击角函数特性曲线，将对应的结果与CFD数值计算结果相结合。同时基于现场给定的5组工况进行数值计算，获得不同工况下的冲蚀结果，并进行端口特性参数对冲蚀作用影响规律的研究。研究结果可为套管端口优化设计提供参考。

1" 计算模型

1.1" SPH模型

SPH法是一种拉格朗日无网格粒子方法。它利用的核函数对物理问题进行近似处理，是众多无网格方法中应用最广泛的一种方法。该方法利用携带有一定物理量（温度、压力、黏度等）的一组粒子集合描述固体与流体等连续相。由于粒子的几何构型直接刻画材料的运动和变形，故SPH法可以直观描述材料界面并追踪材料变形，这些要素在冲击力学数值模拟中极为重要［19–21］。砂粒撞击材料在微观层面上属于冲击，适用于SPH法。

利用SPH方法对目标材料进行多砂粒冲击模拟，获得砂粒对目标材料的冲击特性，验证冲蚀模型中的冲击角函数。在SPH法中，控制方程的表达式如下：

ρit=∑Nj=1mjvijWijxi（1）

vit=-∑Nj=1mjσiρ2i+σjρ2jWijxi（2）

uit=12∑Nj=1mjσiρ2i+σjρ2jvijWijxi（3）

式中：ρ为粒子的密度，kg/m3；t为时间，s；mj为粒子j的质量，kg；vij=vi-vj，为粒子i与j之间的相对速度矢量的分量，m/s；Wij为核函数，m-3；σi、σj分别为粒子i与j的应力张量的分量，Pa；vi为粒子 i的速度，m/s；ui为颗粒的单位质量内能，m2/s2。

本文数值计算中所使用的三次样条核函数是一种常见的核函数［22］，其表达式如下所示：

WR，h=αd23-R2+12R3" 0≤R＜1

162-R3" 1≤R＜2

0" R＞2（4）

R=ri-rj/h（5）

式中：R为点i与j之间的相对距离， m；h为光滑长度，m；αd为核函数归一化系数，在不同维度空间中取值不同，在三维空间中取值为1π32h3;ri和rj分别是粒子i和粒子j的位置向量，m。

图1为SPH核函数示意图。

1.2" Johnson-Cook模型

Johnson-Cook 模型适用于大变形、高应变率下的材料力学响应，被广泛应用于粒子冲击的数值模拟中［23］。砂粒冲击壁面在微观结构上属于大形变冲击问题，故使用该模型对目标材料的力学响应进行描述。Johnson-Cook 模型［24］包括本构模型与失效模型，本构模型用于描述套管材料的弹塑性力学行为，失效模型用于计算材料的失效行为，其形式如下：

σeq=A+Bεneq1+Clnε*1-T*m（6）

T*=T-Tr/Tm-Tr（7）

εf=D1+D2expD3σ*1+D4lnε*

1+D5T*（8）

式中：σeq为材料的流动应力，Pa；A、B为屈服强度和应变硬化系数，Pa；ε*为等效塑性应变率与参考应变率的比值，无量纲；T为材料的当前温度，K；Tr为材料的室温，K；Tm为材料的熔点，K；n为材料应变硬化指数； C为应变率敏感系数；m为温度软化指数；εeq为等效塑性应变；εf为失效应变；D1、D2、D3为应力三轴度影响系数；D4为应变率敏感系数；D5为温度敏感系数；σ*为等效应力与平均应力的比值，无量纲。

套管材料为42CrMo，数据来源见文献［25］，取值如表 1与表 2所示。

1.3" 颗粒追踪模型

含砂压裂液在套管中的流动属于固-液两相流动，其中压裂液为连续相，砂粒为离散相。在湍流的作用下，颗粒与流体之间相互作用，其控制方程如下：

dvpdt=FDv-vp+gρp-ρsρp+Fz（9）

FD=3μCDRe4ρpd2p（10）

Re=ρdpvp-vμ（11）

式中：vp为颗粒流速，m/s；v为流场速度，m/s；ρp为颗粒密度，kg/m3;ρs为流体密度，kg/m3；g为重力加速度，m/s2；Fz为单位质量附加外力，N/kg;FD（v-vp）为单位质量曳力，N/kg；Re为相对雷诺数，无量纲；μ为流体动力黏度，Pa·s；dp为颗粒直径，m；Cd为曳力系数，无量纲。

1.4" 冲蚀模型

冲蚀作用过程复杂，受到多种因素影响，在数值模拟中一般利用冲蚀公式进行预测。选用的Oka冲蚀模型考虑了粒子冲击速度、粒子粒径、冲击角函数与目标材料物性参数。Oka冲蚀模型方程如下［26-28］：

ER=ρtkfαHvk1vpv′k2dpd′k3（12）

fα=sin αn11+Hv1-sin αn2（13）

式中：ER为冲蚀率，kg/（m2·s）；fα为冲击角函数；k、k1、k2、k3、n1、n2为给定常数；Hv为材料维氏硬度，HV；v′为参考速度，vp为粒子实际速度，m/s；d′为参考粒径，m。

冲击角函数表征撞击角度与冲蚀作用之间的关系。

2" SPH法模拟砂粒冲击套管材料

构建的三维微观撞击模型如图 2所示。计算多个球形砂粒对同一位置的撞击结果，砂粒之间互不影响；模拟中设置8个砂粒以不同角度对同一位置的多次撞击，具体如图 3所示。在t=0时刻对目标材料进行SPH粒子转换。

撞击角度与速度分布如表 3所示。冲击速度取Oka冲蚀公式推导所用试验数据，冲击角度为速度方向与水平方向夹角。

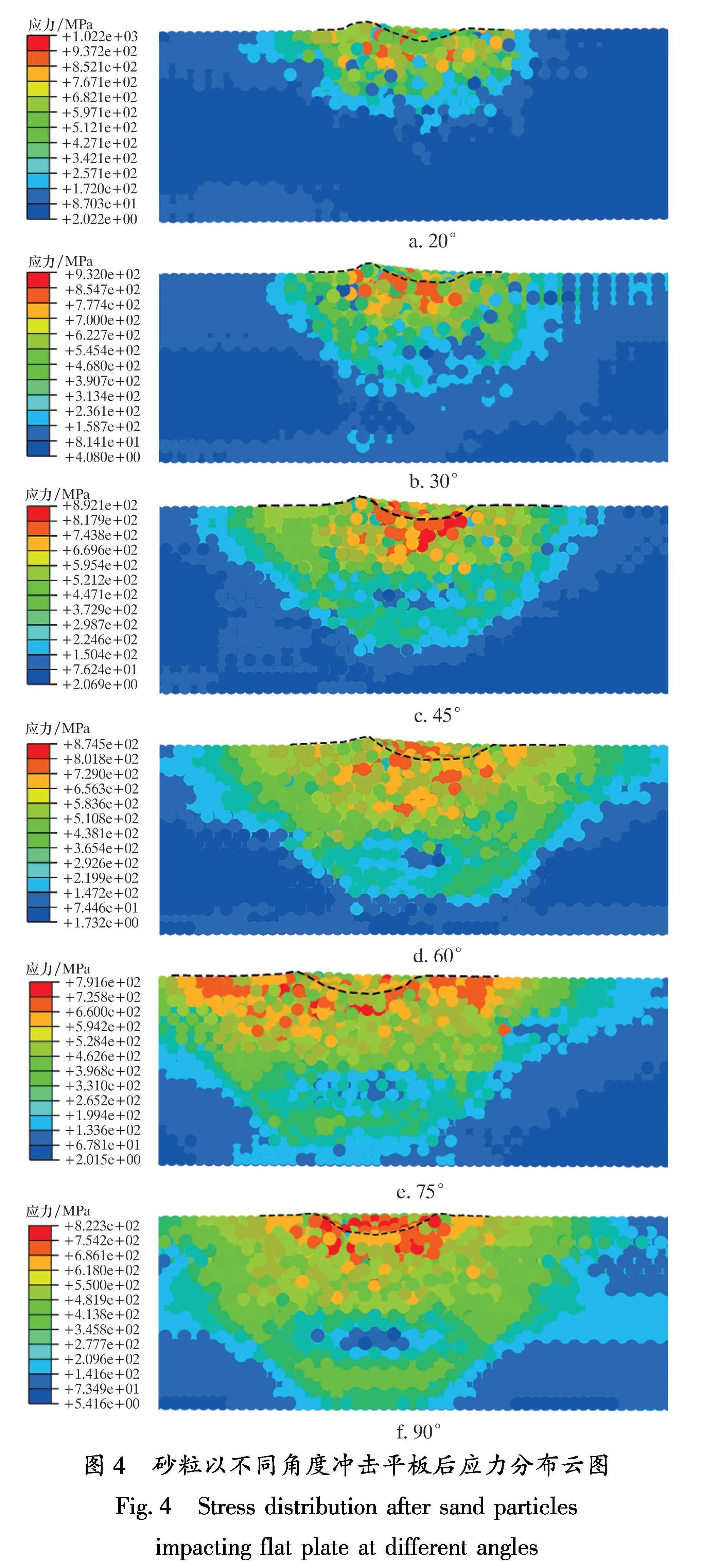
对于高角度冲击，垂直速度分量较大，材料受到挤压发生变形形成两边微微凸起，中部下陷的冲击坑，凸起在被其他粒子冲击后，容易形成碎屑而脱落。对于低角度冲击，水平方向速度分量更大，同时又具有一定程度的垂直速度分量，形成了剪切样貌的冲击坑，突起更高，会更容易引发冲蚀效果。在20°～45°的入射角度范围内，所形成的突起更高，在实际冲蚀情况下更容易被后续粒子冲击发生剪切作用，导致材料损失。随着冲击角度逐渐降低，目标材料中的最大应力值也在增加。由于低角度冲击材料后表面硬化，且砂粒与目标材料之间发生滑移，砂粒在撞击过程中仅部分动能转化为目标材料内能，故图4中低冲击角度影响范围较小，而高角度冲击下，由于速度垂直分量较大，更多动能转化为目标材料内能，影响范围较大。

在冲击过程中，材料发生塑性变形而导致材料失效，以塑性应变作为失效参考依据，同时依据冲击角函数处理方法处理模拟数据。无量纲化冲蚀量E依据90°下冲击角对应冲蚀量进行标准化处理，计算公式如下：

E=EαE90（14）

式中：E为无量纲化冲蚀损失质量；Eα为在冲击角度为α时的冲蚀损失质量，mm2/a；E90为冲击角度在90°时的冲蚀损失质量，mm2/a。

无量纲冲蚀速率与冲击角度的关系如图 5所示。由图5可知，冲蚀作用随着冲击角度的增大而加强，达到最大冲蚀作用后则会出现减弱趋势，该趋势与Oka冲蚀模型中冲击角函数趋势一致。

erosion rate and impact angle

同时，模拟结果与Oka冲蚀模型曲线中均存在冲击角度为20°～45°时冲蚀作用较为强烈，随后逐渐减弱。虽然高角度冲击比低角度下冲击的影响范围大，但低角度下的冲蚀量比高角度下冲击大。在冲击角函数中，也将目标材料硬度作为一个影响因素。对于大多数金属来说，重复变形部分为定值，故n1部分取原Oka模型中默认值（n1=0.8）。冲击角函数分为重复变形与切削，如图 6所示。

3" 套管滑套流场与内壁冲蚀计算

3.1" 几何模型

套管滑套结构如同7所示。根据现场套管滑套模型，套管最大外径为177 mm，在端口处内径为154 mm，滑套内径为124 mm，总长度为1 136 mm，端口形状为胶囊形，长为74 mm，宽为20 mm。提取的流体域利用六面体网格与多面体网格共节点，进一步提升网格整体质量。图8为套管及滑套流场域计算网格。

3.2" 冲蚀计算

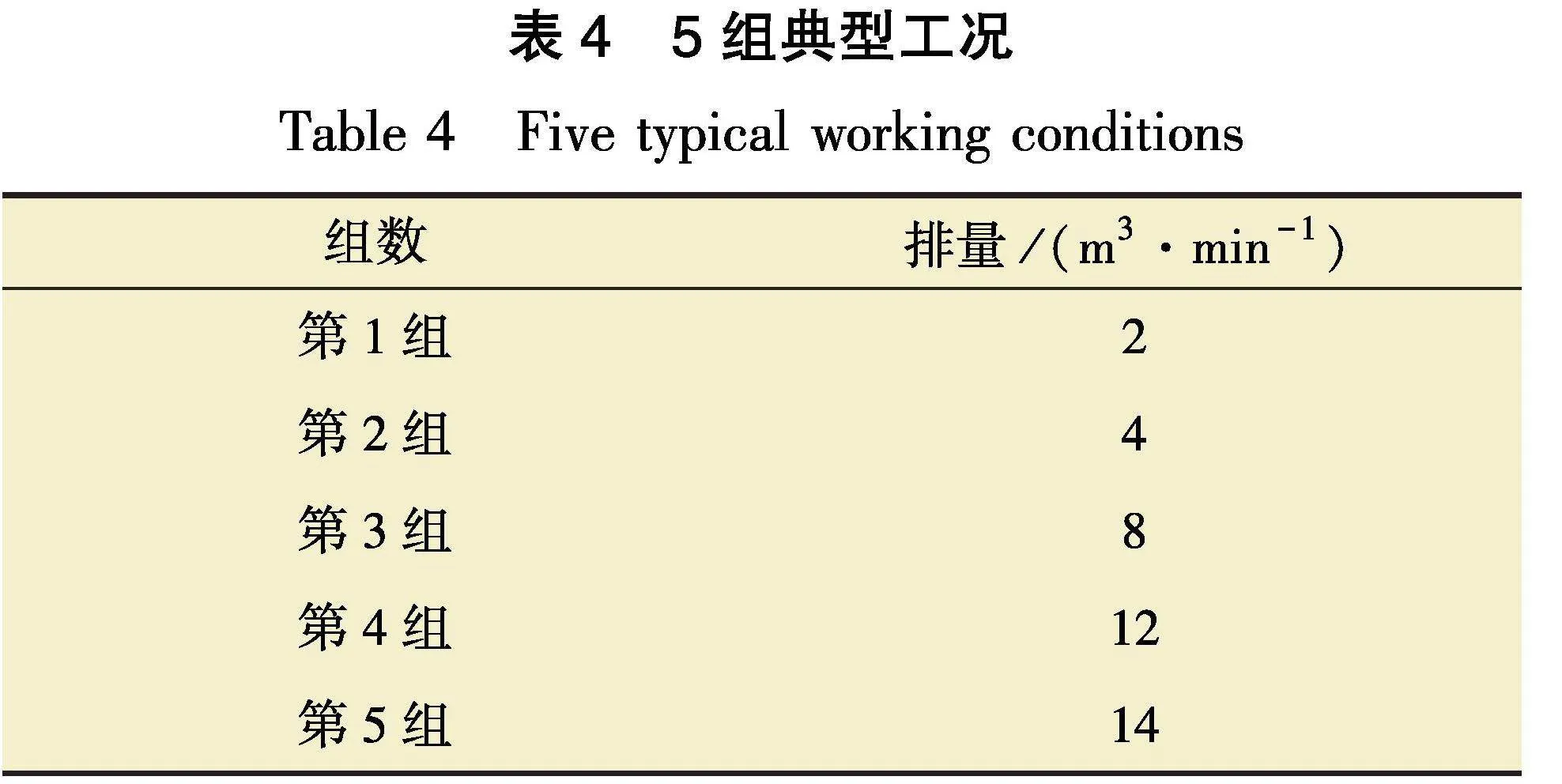
对端口进行5组典型工况计算，如表4所示。计算中所采用压裂液为EM30S，其密度为1 100 kg/m3，黏度为99 mPa瘙簚s，所用砂粒是粒径为380、830 μm的石英砂，其体积密度为1 470 kg/m3，视密

度为2 620 kg/m3，含砂体积分数均设置为参考值10%。以上各个参数均于离散相选项中进行设置。

5组工况下套管冲蚀速率分布云图如图9所示。由图9可知，在不同工况下套管损伤严重的区域几乎一致，在端口附近其冲蚀作用更为明显。从整体上看，冲蚀作用主要集中在套管的前半部分。由于流体几乎从端口处流出，在后半段中因封闭导致流体几乎无法流动，砂粒运动速度也较小，故其冲蚀作用不明显。

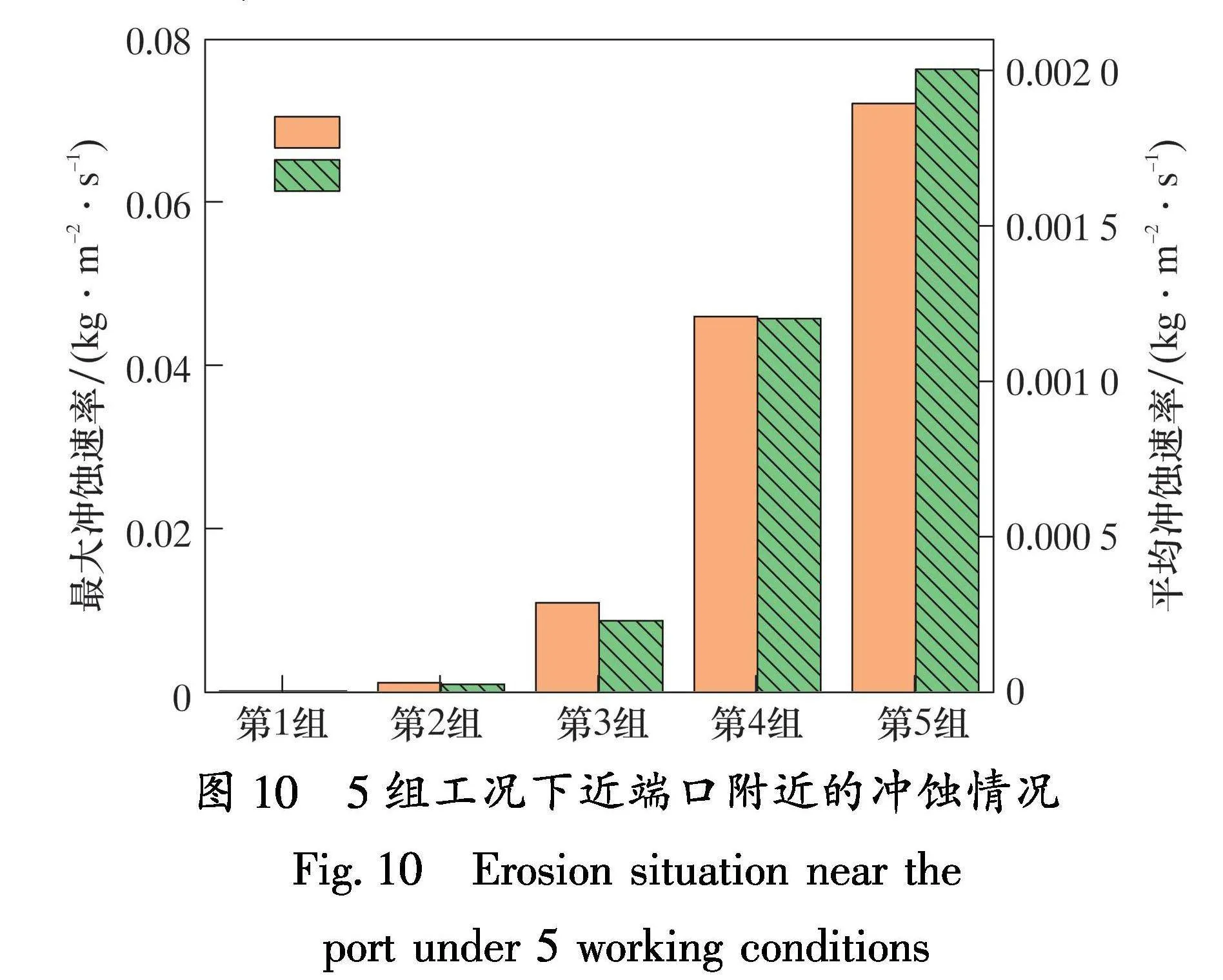
5组工况下近端口附近的冲蚀情况如图 10所示。由图10可知：在低排量时，砂粒的速度相对较小，其对套管内壁的冲蚀作用不强，导致靠近端口处冲蚀速率较小；随着排量的增大，砂粒在套管中的速度也随之增大，在第3、4、5组工况下最大冲蚀速率和平均冲蚀速率增长速度比第1、2组工况下更高，冲蚀作用也更为明显。

port under 5 working conditions

3.3" 端口特性冲蚀影响因素

端口特性会影响套管端口出处壁面的冲蚀作用。这里选用端口数量、端口面积与端口形状共3种因素进行分析。由于篇幅所限，以下分析均基于第3组工况。

3.3.1" 端口数量

端口作为套管中的流体出口，其数量影响套管端口附近的流场。考虑到现场生产，2端口套管通流面积过于狭小，不适合大排量的固井滑套压裂；10端口对套管结构破坏较大，容易引发套管破坏等安全问题。故在每个端口面积相同的情况下，设计了4端口、6端口、8端口模型，如图11所示。

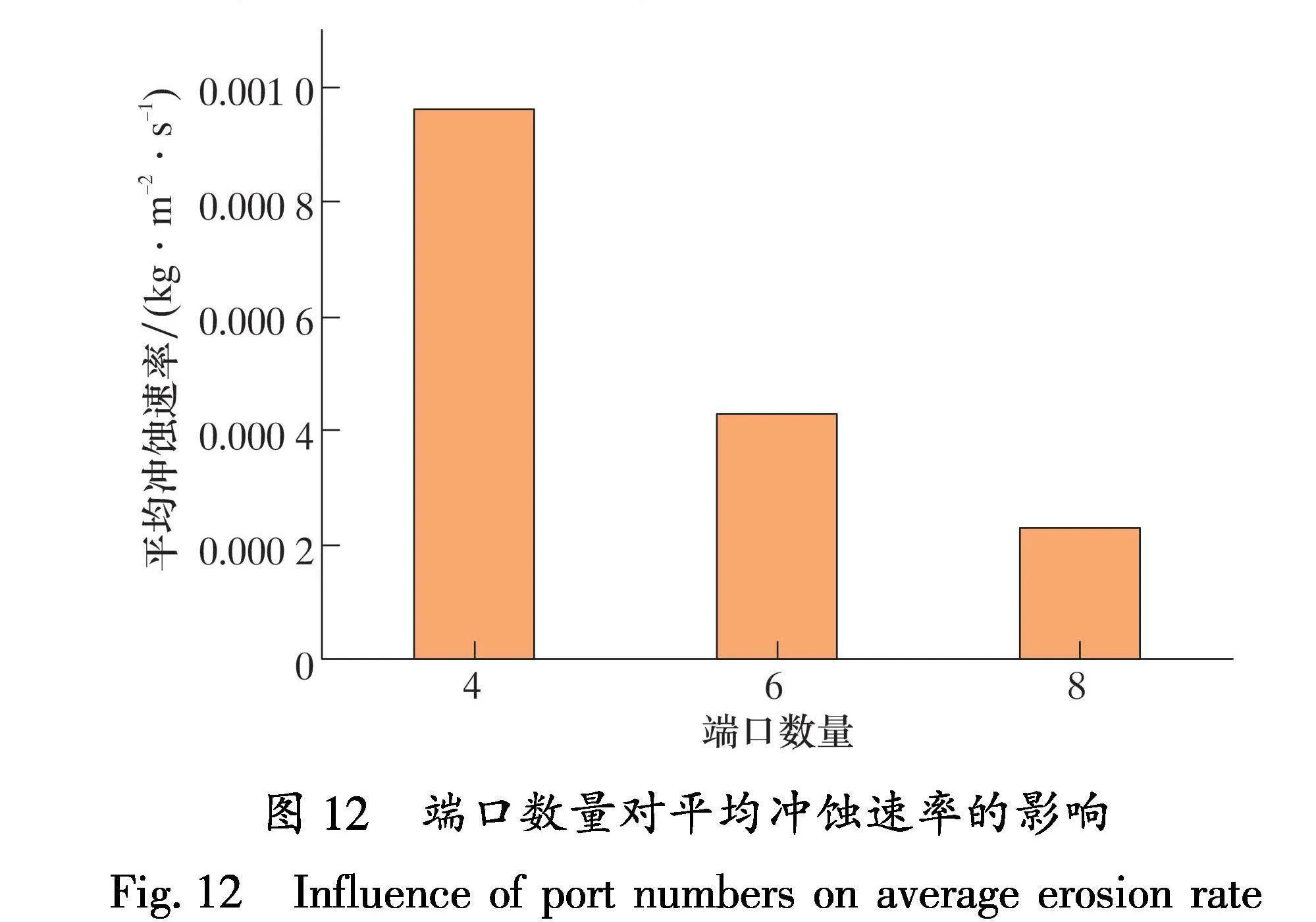
为了更好地分析端口数量对冲蚀的影响，将端口及其附近区域单独截取，对该部分冲蚀速率做平均计算处理。端口数量对平均冲蚀速率的影响如图 12所示。由图12可知：随着端口数量的增加，端口附近的平均冲蚀速率呈现下降的趋势，平均冲蚀速率：由4端口的9.65×10-4 kg/（m2·s）下降至8端口的2.30×10-4 kg/（m2·s），下降幅度为73.8%；冲蚀速率随着端口数目增多而呈现出较为明显的下降，但其下降的趋势逐渐减弱。虽然无法无限制增加端口数目，在允许范围内增加端口数目可以减轻端口冲蚀作用。

3.3.2" 端口面积

端口面积也是影响冲蚀的一个主要因素。为了探究端口面积对冲蚀速率的影响，保持其端口形状为胶囊形，分别对4种面积的胶囊形端口进行计算。端口尺寸如图 13所示。

端口面积对平均冲蚀速率的影响如图 14所示。由图14可知，随着端口面积的增大，平均冲蚀速率逐渐减小，面积为1 000 mm2端口的平均

冲蚀速率为3.64×10-4 kg/（m2·s），而面积为1 600 mm2端口的平均冲蚀速率为2.1×10-4 kg/（m2·s）。平均冲蚀速率随端口面积增大而减小，故在允许范围内，应当尽量增大固井滑套端口处的面积。

3.3.3" 端口形状

在研究中发现，端口形状在一定程度上影响着端口及其附近的冲蚀情况。分别对矩形、菱形、胶囊形、椭圆形4种类型的端口（见图15）进行计算，结果如图16所示。

如图 16所示，在4种相同面积的端口中，平均冲蚀速率最高的端口形状为矩形端口，椭圆形与菱形端口的平均冲蚀速率相近，这表明它们更加流线型的边缘可能有助于减轻流体引起的冲蚀作用。胶囊形端口对应的平均冲蚀速率最低，其流线型设计优化了流体流过端口的路径，最小化了流体对端口壁面的直接撞击和湍流强度，在4种端口类型中显示出最佳的抗冲蚀性能，相比于矩形端口其抗冲蚀性能提高了35.2%。说明端口形状对端口周围流场有着较大的影响，不同类型的端口形状有着不同的抗冲蚀特性，在无其他特殊要求时，应选择胶囊形端口。

4" 结" 论

（1）通过建立连续砂粒冲蚀磨损仿真模型，利用光滑粒子法分析了砂粒连续冲击材料时所发生的特征现象，结果表明，滑套材料42CrMo钢在冲击角度为20°～45°时有更大的冲蚀损失，其冲蚀规律与Oka冲蚀模型相符，也符合42CrMo钢的金属特性。

（2）通过CFD数值模拟5组不同工况下的套管冲蚀过程，结果表明，在整个固井滑套内壁中，冲蚀最严重的区域出现在端口及其附近，主要原因为出口处出流速增加导致砂粒撞击的速度增加，进而使冲蚀速率明显增大。

（3）端口的特性参数对套管及其附近的冲蚀有着明显的影响，其影响因素包括端口数目、端口面积以及端口形状。随着端口数目的增加，平均冲蚀速率会在一定程度内降低，但是降低的趋势明显减缓；随着端口面积增加，平均冲蚀速率会降低，但是降低的趋势也随之减缓；端口形状对冲蚀速率的影响也较大，胶囊形端口的抗冲蚀效果最好。合理选择端口的特性参数能在一定程度上减轻固井滑套的冲蚀磨损。

［1］" "关皓纶，王兆会，刘斌辉．分段压裂固井滑套的研制现状及展望［J］．石油机械，2021，49（11）：84-92．

GUAN H G， WANG Z H， LIU B H. The technical states of cementing sliding sleeve for staged fracturing［J］. China Petroleum Machinery， 2021， 49（11）： 84-92.

［2］" 叶昊，陈林娅，周鸿翔，等．油气管道弯管肘部二次流动侵蚀数值模拟［J］．石油机械，2023，51（4）：119-126．

YE H， CHEN L Y， ZHOU H X， et al. Numerical simulation on secondary flow erosion at elbow of oil and gas pipeline［J］. China Petroleum Machinery， 2023， 51（4）： 119-126.

［3］" 涂亚东，徐小兵，殷华锋，等．高压管汇冲蚀磨损规律研究［J］．石油机械，2018，46（2）：84-88．

TU Y D， XU X B， YIN H F， et al. Analysis on erosion wear laws of high pressure manifold［J］. China Petroleum Machinery， 2018， 46（2）： 84-88.

［4］" 张继信，康健，樊建春，等．高压弯管冲蚀失效分析及数值模拟［J］．润滑与密封，2016，41（10）：40-46．

ZHANG J X， KANG J， FAN J C， et al. Failure analysis and numerical simulation of high pressure elbow erosion wear［J］. Lubrication Engineering， 2016， 41（10）： 40-46.

［5］" 莫丽，刘栖，许先雨．基于CFD数值模拟的异面三通管冲蚀磨损规律研究［J］．润滑与密封，2022，47（8）：41-46．

MO L， LIU Q， XU X Y. Study on erosion wear law of tee in different planes based on CFD numerical simulation［J］. Lubrication Engineering， 2022， 47（8）： 41-46.

［6］" 王川，谢真强，王国荣，等．基于CFD的固井滑套冲蚀特性分析［J］．机械设计，2016，33（7）：66-70．

WANG C， XIE Z Q， WANG G R， et al. Erosion feature analysis of cementing sliding sleeve based on CFD simulation［J］. Journal of Machine Design， 2016， 33（7）： 66-70.

［7］" 魏辽，韩峰，陈涛，等．套管固井滑套冲蚀磨损模拟分析与试验研究［J］．石油钻探技术，2014，42（3）：108-111．

WEI L， HAN F， CHEN T， et al. Analysis and experimental research on erosion of cementing sliding sleeve［J］. Petroleum Drilling Techniques， 2014， 42（3）： 108-111.

［8］" WONG C Y， SOLNORDAL C， SWALLOW A， et al. Predicting the material loss around a hole due to sand erosion［J］. Wear， 2012， 276/277： 1-15.

［9］" XU Y Q， GUAN Z C， LIU Y W， et al. Structural optimization of downhole float valve via computational fluid dynamics［J］. Engineering Failure Analysis， 2014， 44： 85-94.

［10］" 向正新，李思行，钱利勤，等．压裂球座冲蚀磨损规律研究和结构优化［J］．工程设计学报，2017，24（5）：555-562．

XIANG Z X， LI S H， QIAN L Q， et al. Study on erosion law and structure optimization of fracturing ball seat［J］. Chinese Journal of Engineering Design， 2017， 24（5）： 555-562.

［11］" PARSI M， NAJMI K， NAJAFIFARD F， et al. A comprehensive review of solid particle erosion modeling for oil and gas wells and pipelines applications［J］. Journal of Natural Gas Science and Engineering， 2014， 21： 850-873.

［12］" DONG X W， LIU G R， LI Z L， et al. A smoothed particle hydrodynamics （SPH） model for simulating surface erosion by impacts of foreign particles［J］. Tribology International， 2016， 95： 267-278.

［13］" DONG X W， LI Z L， FENG L， et al. Modeling， simulation， and analysis of the impact（s） of single angular-type particles on ductile surfaces using smoothed particle hydrodynamics［J］. Powder Technology， 2017， 318： 363-382.

［14］" TAKAFFOLI M， PAPINI M. Material deformation and removal due to single particle impacts on ductile materials using smoothed particle hydrodynamics［J］. Wear， 2012， 274/275： 50-59.

［15］" AZIMIAN M， SCHMITT P， BART H J. Numerical investigation of single and multi impacts of angular particles on ductile surfaces［J］. Wear， 2015， 342/343： 252-261.

［16］" HADAVI V， PAPINI M. Numerical modeling of particle embedment during solid particle erosion of ductile materials［J］. Wear， 2015， 342/343： 310-321.

［17］" 廖翔云，马小晶，周新超，等．基于SPH方法的组合射流破岩模拟研究［J］．石油机械，2022，50（5）：1-8．

LIAO X Y， MA X J， ZHOU X C， et al. Numerical simulation of rock breaking by combined Jets based on SPH method［J］. China Petroleum Machinery， 2022， 50（5）： 1-8.

［18］" 王方祥，杨仲才，赵增权，等．压裂液返排期间放喷油嘴的磨损规律研究［J］．石油机械，2020，48（1）：102-109．

WANG F X， YANG Z C， ZHAO Z Q， et al. Study on erosion wear of discharge nozzle during fracturing fluid backflow［J］. China Petroleum Machinery， 2020， 48（1）： 102-109.

［19］" 杜明超，李增亮，董祥伟，等．菱形颗粒冲击材料表面冲蚀磨损特性分析［J］．摩擦学学报，2020，40（1）：1-11．

DU M C， LI Z L， DONG X W， et al. Analysis of material surface erosion characteristics due to rhomboid-shaped particle impact［J］. Tribology， 2020， 40（1）： 1-11.

［20］" 靳绍虎，刘科伟，黄进，等．基于Lagrange及SPH算法的花岗岩侵彻数值模拟［J］．高压物理学报，2021，35（5）：143-155．

JIN S H， LIU K W， HUANG J， et al. Numerical simulation of granite penetration based on Lagrange and SPH algorithm［J］. Chinese Journal of High Pressure Physics， 2021， 35（5）： 143-155.

［21］" HE Q G， CHEN X W， CHEN J F. Finite element-smoothed particle hydrodynamics adaptive method in simulating debris cloud［J］. Acta Astronautica， 2020， 175： 99-117.

［22］" 刘维平，张永祥．SPH方法在溃坝数值模拟中的应用［J］．重庆大学学报，2017，40（11）：11-19．

LIU W P， ZHANG Y X. Application of SPH method to numerical simulation of dam-break［J］. Journal of Chongqing University（Natural Science Edition）， 2017， 40（11）： 11-19.

［23］" 舒畅，程礼，许煜．Johnson-Cook本构模型参数估计研究［J］．中国有色金属学报，2020，30（5）：1073-1083．

SHU C， CHENG L， XU Y. Research on parameter estimation of Johnson-Cook constitutive model［J］. The Chinese Journal of Nonferrous Metals， 2020， 30（5）： 1073-1083.

［24］" JOHNSON G R， COOK W H. Fracture characteristics of three metals subjected to various strains， strain rates， temperatures and pressures［J］. Engineering Fracture Mechanics， 1985， 21（1）： 31-48.

［25］" NING J Q， LIANG S Y. Model-driven determination of Johnson-Cook material constants using temperature and force measurements［J］. The International Journal of Advanced Manufacturing Technology， 2018， 97（1）： 1053-1060.

［26］" OKA Y I， OKAMURA K， YOSHIDA T. Practical estimation of erosion damage caused by solid particle impact： Part 1： Effects of impact parameters on a predictive equation［J］. Wear， 2005， 259（1/2/3/4/5/6）： 95-101.

［27］" OKA Y I， YOSHIDA T. Practical estimation of erosion damage caused by solid particle impact： part 2： mechanical properties of materials directly associated with erosion damage［J］. Wear， 2005， 259（1/2/3/4/5/6）： 102-109.

［28］" 卓仁燕， 马新仿， 李建民， 等. 水平井限流压裂对射孔孔眼冲蚀的影响［J］. 钻采工艺， 2023， 46（2）： 77-82.

ZHUO R Y， MA X F， LI J M， et al. Effect of Limited Entry Fracturing for Horizontal Wells on Perforation Erosion［J］. Drilling amp; Production Technology， 2023， 46（2）： 77-82.

第一张磊，副教授，生于1983年，博士，研究方向为多相流数值模拟。地址：（102249）北京市昌平区。电话：（010）89733537。email： zlei@cup.edu.cn。

2024-01-28" 修改稿收到日期：2024-07-15

刘锋