高考中的概率与统计问题例析

概率与统计作为数学的一个分支，在近些年的高考中占了很大的比重。概率板块的重要知识点是计数原理与排列组合（二项式定理），随机事件的概率，概率分布（二项分布、超几何分布、正态分布）;统计板块的重要知识点是统计图表和成对数据的统计分析。本文选取2024年高考数学中概率与统计的部分真题与模拟题，并给出解法探析，希望对参加2025年高考的同学有所启迪。

考点一、计数原理及概率

例1（2024年全国甲卷文科）某独唱比赛的决赛阶段共有甲、乙、丙、丁四人参加，每人出场一次，出场次序由随机抽签确定，则丙不是第一个出场，且甲或乙最后出场的概率是（）。

A.1/6B.1/4C.1/3D.1/2

解法一：四个人由随机抽签的方式确定出场顺序，基本事件总共有A44=24（个）。

满足丙不是第一个出场，且甲或乙最后出场的基本事件为：（甲，丙，丁，乙），（甲，丁，丙，乙），（丁，丙，甲，乙），（丁，甲，丙，乙），（乙，丙，丁，甲），（乙，丁，丙，甲），（丁，丙，乙，甲），（丁，乙，丙，甲），共有8个。

所以丙不是第一个出场，且甲或乙最后出场的概率为P=8/24=1/3。

解法二：四个人由随机抽签的方式确定出场顺序，基本事件总共有A44=24（个）。

由于丙不在第一个出场，且甲或乙最后出场，所以丙只能是第二或第三个出场，有2种情况，第四个出场的是甲或乙，有2种情况，剩下的两个人出场有A22=2（种）情况，由乘法原理得满足丙不是第一个出场，且甲或乙最后出场的基本事件有2×2×2=8（个），所以所求概率为P=8/24=1/3。

故选C。

点评：对于排列组合问题，我们可以通过特殊元素优先考虑安排，再结合加法原理和乘法原理进行解决，必要的时候要分情况讨论，当然如果排列组合的基本事件个数不多，也可以用列举法解决。

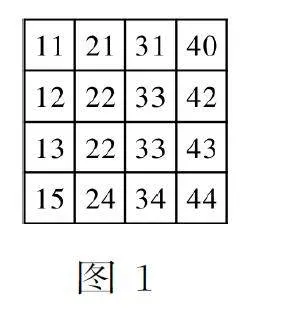
例2（2024年新课标全国Ⅱ卷）在图1所示的4×4的方格表中选4个方格，要求每行和每列均恰有一个方格被选中，则共有______种选法;在所有符合上述要求的选法中，选中方格中的4个数之和的最大值是______。

解析：每行和每列均恰有一个方格被选中，首先在第一行选一个数，有4种选择方式;接下来在第二行中任取一个方格，但不能与第一行选取的方格同列，这样有3种选择方式;接着在第三行中任取一个方格，但不能与前面选取的两个方格同列，这样有2种选择方式;最后在第四行中任取一个方格，但不能与前面选取的三个方格同列，这样有1种选择方式。由乘法原理知，选法共有4×3×2×1=24（种）。也可以依次考虑每一列的方格，方法和结论均相同。

因此第一个空的答案为24。

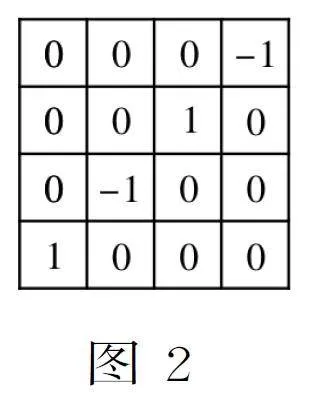
将第一列的每个数同时减去10，这样无论最后选择的是哪四个方格，这四个数的和都减少了10，同理，将第二列的每个数同时减去20，第三列的每个数同时减去30，第四列的每个数同时减去40。接下来，将第一行的每个数同时减去1，第二行的每个数同时减去2，第三行的每个数同时减去3，第四行的每个数同时减去4。这样就转化为在图2所示的方格表中选择四个方格，要求每行每列都恰有一个方格，且使得被选出的方格内的数之和最大，然后将这个最大值加上10+20+30+40+1+2+3+4=110，即为答案。

点评：同学们在解决正态分布的问题时，需要抓住两点：一是找准u±σ，u±2σ，u±3σ这六个数值;二是充分利用正态密度函数图像的对称性求解，如P（Xgt;u+σ）=P（Xlt;u-σ）。

考点四、统计（图）表特征数据分析

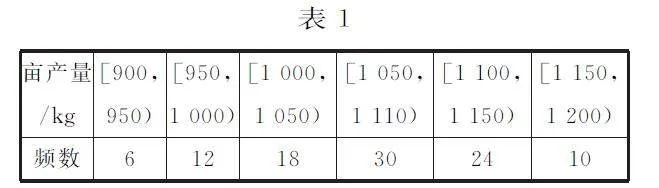
例6（2024年新课标全国Ⅱ卷）某农业研究部门在面积相等的100块稻田上种植一种新型水稻，得到各块稻田的亩产量（单位：kg）并整理得表1：

根据表中数据，下列结论中正确的是（）。

A.100块稻田亩产量的中位数小于1050kg

B.100块稻田中亩产量低于1100kg的稻田所占比例超过80%

C.100块稻田亩产量的极差介于200kg至300kg之间

D.100块稻田亩产量的平均值介于900kg至1000kg之间

解析：从频数分布表可以看出，在100块稻田中，亩产量低于1050kg的稻田有6+12+18=36（块），亩产量不低于1050kg的稻田有100-36=64（块），所以这100块稻田亩产量的中位数一定不小于1050kg，故选项A错误。

在100块稻田中，亩产量低于1100kg的稻田有6+12+18+30=66（块），所以其所占比例为66%，故选项B错误。

极差为一组数据中最大值与最小值的差，从频数分布表可以看出，在100块稻田中，亩产量的最大值大于等于1150kg，小于1200kg，而亩产量的最小值大于等于900kg，小于950kg，所以这100块稻田亩产量的极差的最小值大于1150-950=200（kg），极差的最大值小于1200-900=300（kg），即极差介于200kg至300kg之间，故选项C正确。

这100块稻田亩产量的平均值最小为1/100（900×6+950×12+1000×18+1050×30+1100×24+1150×10）=1042（kg），故选项D错误。

故选C。

点评：同学们在解答统计问题时，要会从频数分布表（频率分布直方图）中提取数据信息，能计算特征数据，如平均数、中位数、极差、方差、标准差等，并利用样本的规律估计总体的规律。

例7（2024年济南模拟卷）已知随机变量X～N（1，22），则D（2X+1）的值为______。

解析：因为X～N（1，22），所以D（X）=22=4，D（2X+1）=22D（X）=4×4=16。

故填16。

点评：对于二项分布X～N（u，σ2），其中σ2为二项分布的方差，即D（X）=σ2，而对于期望和方差有结论：E（aX+b）=aE（X）+b，D（aX+b）=a2D（X）。

考点五、成对数据的统计分析

例8（2024年苏锡常镇调研一卷）已知变量x，y的统计数据如表2，对表中数据作分析，发现y与x之间具有线性相关关系，利用最小二乘法，计算得到经验回归方程为^y=0.8x+^a，据此模型预测，当x=10时，^y的值为______。

解析：由表2中的数据得x=7，y=5，所以5=0.8×7+^a，解得^a=-0.6，所以^y=0.8x-0.6。所以当x=10时，^y=0.8×10-0.6=7.4。

故填7.4。

点评：在线性相关关系中，经验回归方程一定过样本中心点（x，y），依此求出参数^a的值，从而可以预测x=10时^y的值。

虽然概率与统计板块在近几年的高考中经常出题，但难度不大，在平时的复习中，只要重视基础知识，如基本概念、基本逻辑关系，提高运算能力，就能正确解决概率与统计问题。

（责任编辑王福华）