中华优秀传统文化融入小初高数学课堂的一体化教学设计探析

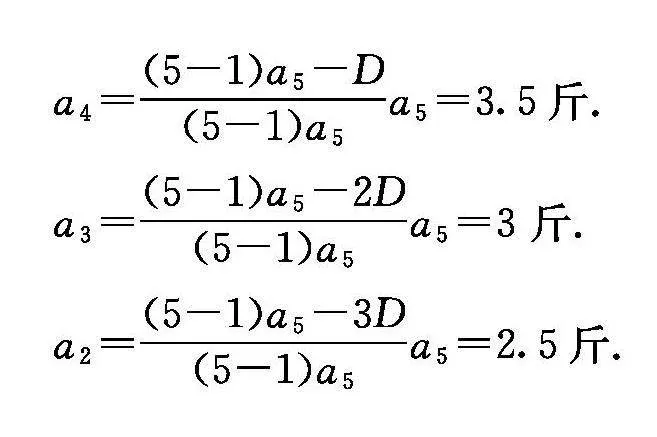
摘" 要：我国古代数学成就是中华优秀传统文化的有机组成部分，其背后的数学古典名题是中华民族文明及数学文明的载体形式，挖掘背后的意蕴将做到古今对接，启迪数学思维，强化经典意识.构建可操作性的一体化教学模式可使中华优秀传统文化真正有机融入课堂教学中.

关键词：中华优秀传统文化；课堂教学；数学典籍

基金项目：2023年度伊犁师范大学研究生教育创新计划项目“中华优秀传统文化课程资源开发及教学路径探索”（项目编号：XJ2024G263）；

2023年度自治区高校本科教育教学研究和改革项目“一流本科课程建设视域下小学教育专业课堂教学模式创新研究与实践” （项目编号：XJGXZHJG202336）；伊犁师范大学提升学科综合实力专项一般项目“义务教育阶段学生学业质量的影响因素分析与提升研究”（项目编号：22XKSY29）.

2021年中华人民共和国教育部颁布的《中华优秀传统文化进中小学课程教材指南》（以下简称《指南》）指出：“我国古代数学成就是中华优秀传统文化的有机组成部分.”同时，“继承和弘扬中华优秀传统文化”是《义务教育数学课程标准（2022年版）》和《普通高中数学课程标准（2017年版2020年修订）》的共同要求.［1］ ［2］但是，目前中华优秀传统文化融入中小学数学教学的研究还处在起步阶段，认识还不够明晰，实践还需加强.［3］特别是从小学、初中、高中三个学段进行一体化教学设计的研究还很缺乏.数学古典名题是我国古代数学成就的主要内容载体.因此，本文以数学古典名题为例，从小初高一体化教学设计出发，探析中华优秀传统文化融入数学课堂的教学目标、教学内容、教学方式和教学评价，以期为中华优秀传统文化有机融入数学教学提供参考．

1" 文化性与数学性相结合，确立融入中华优秀传统文化的教学目标

中华传统文化融入课堂是以人为本，兼具真、善、美三维一体价值谱系的一种基本形式［4］，学生不仅要学习数学知识，更需感悟中华优秀传统文化的意蕴，接受文化熏陶.因此，中华优秀传统文化融入数学课堂的教学必须树立知识目标与文化目标相融合的目标意识.一方面，要意识到中华优秀传统文化中的数学元素蕴涵着丰富的数学知识、思想和方法，是学生数学学习的重要素材；另一方面，要挖掘中华优秀传统文化中数学元素的文化内涵，在中华民族的数学典籍、古代数学成就和数学家的人物传记中认识中华民族古人的数学智慧和创造，感受古代数学家求真创新的精神，不断增强文化认同，培育文化自信．

此外，因学生的数学知识储备和认知能力随年龄增长而不断发展，中华优秀传统文化融入数学课堂的教学目标应呈现出学段间的层次性.根据《指南》要求，小学以培养学生对中华优秀传统文化的亲切感和感受力为主，初中以增强理解力为重点，高中以理性认识和践行能力为重点，因此小学数学教学目标应定位于学生初步了解我国古代数学成就、创造和数学家，初步感受背后蕴含的中国古代数学思想和方法；初中数学教学目标重在通过求解与传统文化相关的数学问题来加深学生对中华优秀传统文化的理解，体悟中华优秀传统文化的魅力；高中数学教学目标应研习我国古代数学成就并应用其来分析、解决问题，在数学探究活动中深入理解我国古代数学的思想和方法，增强对中华优秀传统文化的理性认识并能古为今用．

以《九章算术》中一道题为例，该题原文为“今有金箠，长五尺.斩本一尺，重四斤.斩末一尺，重二斤.问次一尺各重几何”，其意思为“有一根长五尺的金木棍.从头部截取一尺，重四斤.从尾部截取一尺，重两斤.从头至尾依次截得的金木棍质量是均匀变小的，请问中间三尺，每一尺重多少”.结合上述分析，拟定不同学段的教学目标（见表1）.

2" 结合学段内容，实现中华优秀传统文化素材的教学转化

研究发现，中华优秀传统文化融入教科书的比例与数学知识的关联性不高.［5］教师有必要结合数学课程内容挖掘相契合的中华优秀传统文化素材并进行教学转化.一方面是素材的语言转化，中华优秀传统数学文化主要以数学典籍的形式流传下来，其语言以古文记述，较难理解，所以需要教师用现代语言进行转译解读；另一方面是素材的教学转化，教师应对所挖掘的中华优秀传统数学文化素材与学段具体教学内容知识点和学生认知水平结合，进行创造性转化，可采用复制式的方式进行教学处理，即根据中华优秀传统数学文化素材涉及的数学知识与当前的数学课程内容进行对接，找到适合的切入点，直接应用，也可采用顺应式［6］，即根据教学的需要，将中华优秀传统数学文化素材进行合理改编，再运用于数学课堂中．

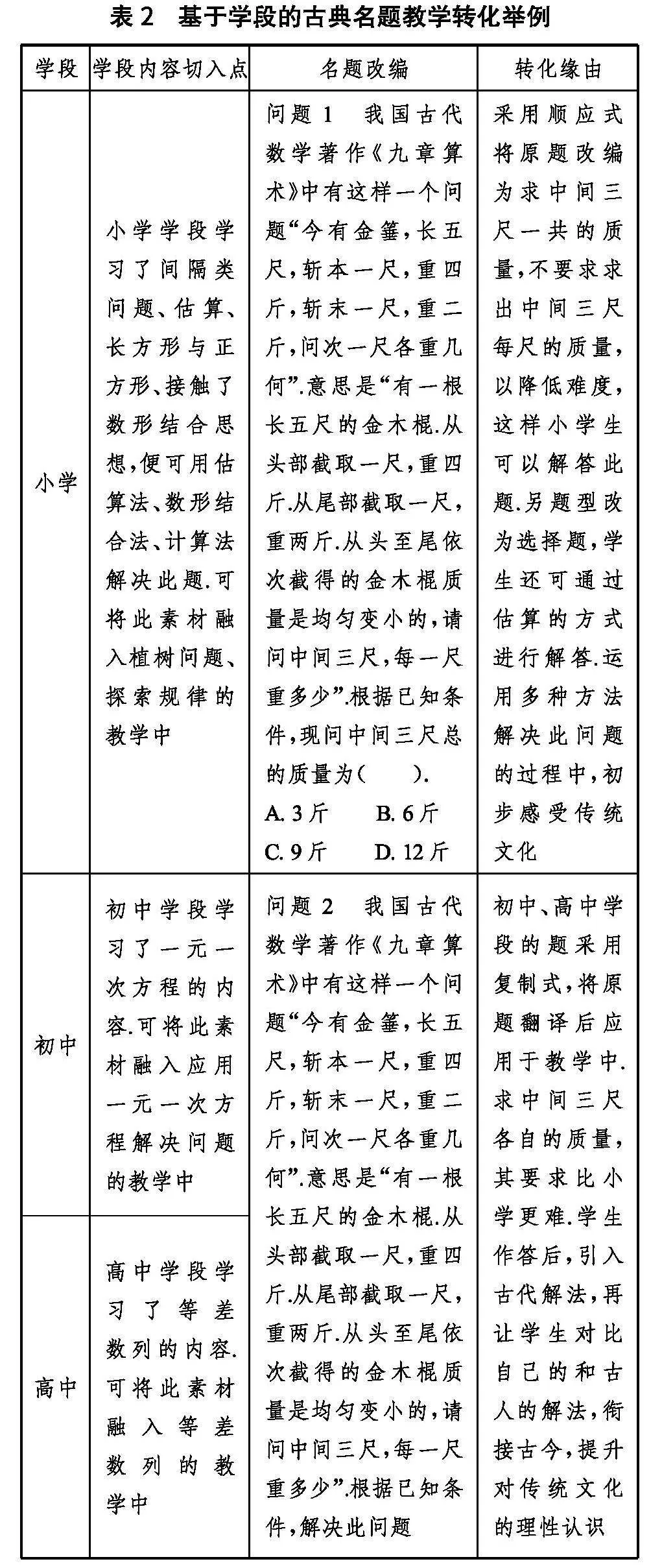
例如，就本文中的古典名题而言，需对此题进行语言转化.本文已对其题目以现代话语翻译，现对这个问题的古代解法进行解读.古代解法原文为令末重减本重，馀即差率也.又置本重，以四间乘之，为下第一衰.副置，以差率减之，每尺各自为衰.副置下第一衰以为法，以本重四斤遍乘列衰，各自为实.如法得一斤. 其意思为“ 先求‘差率’，即将金木棍的头重与尾重相减，再以间数乘本重，作为第一项，然后依次减去差率.最后，用第一项去除所得各项，同时乘本重四斤，即可得到各项”.与此同时，对该题进行教学转化，本文选取的古典名题在小学学段采用顺应式改编后可应用于教学，在初中、高中学段采用复制式可直接应用于教学，如此各学段的学生可以结合所学知识解决问题，具体实例见表2．

初中初中学段学习了一元一次方程的内容.可将此素材融入应用一元一次方程解决问题的教学中

高中高中学段学习了等差数列的内容.可将此素材融入等差数列的教学中

问题2" 我国古代数学著作《九章算术》中有这样一个问题“今有金箠，长五尺，斩本一尺，重四斤，斩末一尺，重二斤，问次一尺各重几何”.意思是“有一根长五尺的金木棍.从头部截取一尺，重四斤.从尾部截取一尺，重两斤.从头至尾依次截得的金木棍质量是均匀变小的，请问中间三尺，每一尺重多少”.根据已知条件，解决此问题初中、高中学段的题采用复制式，将原题翻译后应用于教学中.求中间三尺各自的质量，其要求比小学更难.学生作答后，引入古代解法，再让学生对比自己的和古人的解法，衔接古今，提升对传统文化的理性认识

3" 体现层次性，选择融入中华优秀传统文化的教学方式

中华优秀传统文化融入数学课堂兼具学科属性与文化底蕴，是学生自身文化和优秀传统文化共同赋予知识意义的过程.［7］为搭建桥梁，打通中华优秀传统文化与课堂教学的壁垒，教师应关注学生学习中华优秀传统文化的心路历程.不管是对显性文化知识的了解还是对隐性文化知识的感悟，始终以学生学习为中心，根据中华优秀传统文化教育的学段目标、现行数学课程内容，采用最适切的教学方式.根据《指南》要求，在小学学段重在培育学生对中华优秀传统文化的亲切感和感受力，因此适宜采用多看、多听、多做的体验式教学；初中学段重在增强学生对中华优秀传统文化的理解力，适宜运用基于数学问题解决的启发式教学；高中学段重在增强学生对中华优秀传统文化的理性认识和践行力，强调学生自主反思和应用能力，适合采用自主或合作探究式教学．

以表2中两道名题改编为例，其解法如下所示.小学学段，学生尝试猜想、假设、作图等多种方法解决问题1；初中学段，教师可直接抛出问题，通过提问诱发学生思考，应用一元一次方程来解决问题2，并以留白方式让学生去了解古人解法，为后续学习埋下伏笔；高中学段，学生可采用自主或合作探究去发现应用等差数列知识的求解方法和古代解法的差异，衔接古今对话，触发学生与古人跨时空的思维碰撞，深入理解我国古人的数学智慧．

（1）问题1：估算法.

设最细的一截金木棍为a1=2斤，最粗的一截为a5=4斤，且从最细一截到最粗一截金木棍的质量是均匀增加的，中间三截为a2、a3、a4 ，所以4斤＞a2＞2斤，4斤＞a3＞2斤，4斤＞a4＞2斤，所以（4＋4＋4）斤＞a2＋a3＋a4＞（2＋2＋2）斤，12斤＞a2＋a3＋a4＞6斤.由此可判断9斤属于这个范围.此解法可锻炼学生运算能力和数学思维．

（2）问题1：数形结合法.

设最细的一截金木棍为a1=2斤，最粗的一截为a5=4斤，且从最细一截到最粗一截金木棍的质量是均匀增加的，中间三截为a2、a3、a4 ，运用“凑整”的思想，假设将两根金木棍头尾倒置并排放置，其形态如图1所示.

图1" “凑整”思想示意图

由图可知，a1＋a5=2×a3=a2＋a4=4＋2=6斤，2（a2＋a3＋a4）=3（a1＋a5）=18斤，则中间三尺总质量为a2＋a3＋a4=18÷2=9斤，便求得结果.此解法有利于培养学生的几何直观．

（3）问题1和问题2：计算法.

设最细的一截金木棍为a1=2斤，最粗的一截为a5=4斤，且从最细一截到最粗一截金木棍的质量是均匀增加的，中间三截为a2、a3、a4 .每相邻两截间的质量差值相等且为d=（a5-a1）÷间隔数，间隔数为5-1=4（个），d=（4-2）÷4=0.5斤，a2=a1＋0.5=2.5斤， a3=a2＋0.5=3斤，a4=a3＋0.5=3.5斤.因此，中间三尺总质量为a2＋a3＋a4=9斤.此解法学生需借助解决间隔类问题的方法，算出中间三尺的各自长度，再相加求和，可培养学生的推理意识和运算能力．

（4）问题2：一元一次方程法.

因为金木棍的质量是均匀变化的，设相邻两截间的质量之差为x斤.因最细的一截金木棍为a1=2斤，最粗的一截为a5=4斤，中间三截为a2、a3、a4 .由题意可得a2=a1＋x，a3=a1＋2x，a4=a1＋3x，a5=a1＋4x，所以4=2＋4x，求得x=0.5，所以a2=2.5斤，a3=3斤，a4=3.5斤.此解法有利于培养学生的模型观念．

（5）问题2：等差数列法.

等差数列的通项公式为an=a1＋（n-1）d，设最细的一截金木棍为a1=2斤，最粗的一截为a5=4斤，n=5，直接代入通项公式4=2＋4d，求得公差d=0.5斤.所以a3=a2＋0.5=3斤，a2=a1＋0.5=2.5斤" ，a4=a3＋0.5=3.5斤.此解法有利于培养学生的数学运算素养．

（6）问题2：古代解法.

以下古代解法，用到了公式“ai=an·（n-1）an-（n-i）D（n-1）an”，其中D=an-a1.可令d=an-a1n-1，整理上述公式，得ai=an-（n-i）d．

第一步，求“差率”.因最细的一截金木棍为a1=2斤，最粗的一截为a5=4斤，即“差率”D=a5-a1=2斤.

第二步，用间隔数乘a5作为首项，再依次重复减去“差率”D，得到数列 （5-1）a5，（5-1）a5-D ，（5-1）a5-2D ，（5-1）a5-3D ，（5-1）a5-4D.

第三步，用后面的项除以第一项，同时乘本重4斤，可求得中间三尺各自的质量.

a4=（5-1）a5-D（5-1）a5a5=3.5斤.

a3=（5-1）a5-2D（5-1）a5a5=3 斤.

a2=（5-1）a5-3D（5-1）a5a5=2.5斤．

4" 立足学习体验，实施融入中华优秀传统文化的教学评价

中华优秀传统文化融入数学课堂，能够让学生在学习数学知识，解决数学问题，参与数学活动的过程中达成知识目标和文化目标.文化的理解、认同和传承需要文化教育与学生的生活经验和价值理念产生真实的、有意义的联系，触发学生的情感共鸣，走入学生的内心世界，因此教学评价的关键在于以结合数学知识学习的学生内在体验为主.借鉴学习体验评价框架［8］，中华优秀传统文化融入数学课堂的教学评价，可以从中华优秀传统文化的学习任务体验、学习情境体验、学习活动体验、学习结果体验为评价维度.从学生的体验中去考查学生认知、情感的变化．

小学阶段，从学习任务体验出发，学生在解决本文中古典名题后可询问学生，解决了这个问题后有什么感想；也可从学习活动体验出发，让学生写数学日记，通过回顾反思，进一步增进学生对中华优秀传统文化的认识.初中阶段，从学习情境体验出发，可以给出数学典籍中同类型的问题，让学生完成后相互评阅、交流，在分享互动中展现对古人智慧的感悟和收获.高中阶段，从学习结果体验出发，可让学生自己或组成小组以小课题的形式收集相关的数学古典名题，挖掘史料资源，分析其蕴含的数学思想和方法，提交研究报告或小论文．

中华优秀传统文化蕴涵着博大精深的数学知识、思想与方法，是学生数学学习的宝贵资源.从一体化教学设计的视角出发，有利于形成中华优秀传统文化融入数学课堂的贯通视野，精准把握阶段性要求，有效助力学生学习进阶．

参考文献

［1］中华人民共和国教育部.义务教育数学课程标准（2022年版）［M］.北京：北京师范大学出版社，2022．

［2］中华人民共和国教育部.普通高中数学课程标准（2017年版2020年修订）［M］.北京：人民教育出版社，2020．

［3］曹一鸣.中华优秀传统数学文化进中小学数学课程：从意义到实施［J］.教育研究与评论，2022（6）：46-49．

［4］黄秦安.数学文化视域下数学课堂模式的多元建构［J］.数学通报，2021（8）：11-15．

［5］姜浩哲.我国传统数学文化融入教科书的价值、现状与展望——以人教版小学数学教科书为例［J］.课程·教材·教法，2021（1）：98-104．

［6］陈婷，李兰.中华优秀传统文化融入小学数学教科书：现实样态与行动路向［J］.课程·教材·教法，2021（11）：92-99．

［7］王明娣，翟倩.中华优秀传统文化融入教学的价值、困境及路径［J］.民族教育研究，2020（6）：24-30．

［8］谢翌，曾瑶，丁福军.过程性课程评价论刍议［J］.教育研究，2022（7）：54-64．