俄罗斯方块中的轴对称

1984年的时候，还没有多少人认识阿列克谢，帕基特诺夫．当时，29岁的帕基特诺夫还只是苏联科学院计算机中心的一位普通工程师，他热衷于开发电脑游戏，不过他开发的游戏卖得并不好，那年夏天，他突然想到了一个新点子——让不同形状的积木落进一个长方体容器里，在容器底部堆叠起来．在两位同伴的协助下，他很快编写了这个游戏程序．虽然他预感到这个游戏可能会火，但实际情况还是令他瞠目结舌，这个游戏在莫斯科迅速流行起来，并很快风靡全球．在此后的25年里，这个游戏被移植到了几乎所有的电脑系统和游戏平台上．这个游戏还产生了不计其数的变种，衍生出各式各样的玩法，可以说是解谜游戏大家庭里最重要的成员之一．它就是无人不知无人不晓的经典游戏——俄罗斯方块．

俄罗斯方块的游戏规则非常简单：屏幕上方随机出现一块由小正方形拼成的积木，并不断下落；玩家需要对积木进行旋转，并左右调整积木的位置，让它在一个合适的位置落地．这块积木落地后，屏幕的上方又会出现下一块积木……如果屏幕上的某一行被积木填满，这一行就会被消除，什么时候积木堆到了屏幕的顶端，游戏就结束，玩家就输掉了．

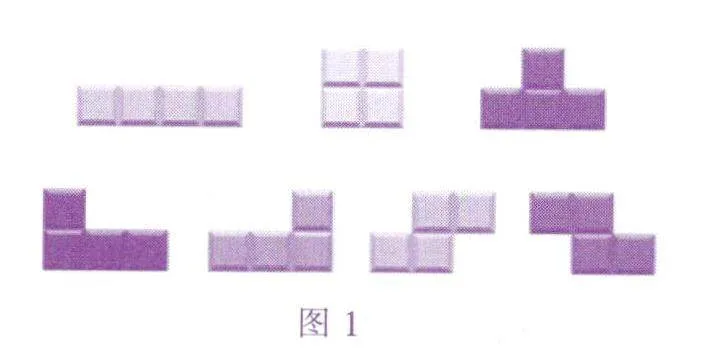
这是一种前所未有的游戏类型，规则简洁而又让人着迷，获得巨大的成功也是理所当然的事情．游戏规则的简洁之处，还与积木的形状有关，俄罗斯方块里的每一种积木都恰好由4个小正方形拼成，因此，俄罗斯方块里的积木只有7种（如图1）．

大家可能会觉得奇怪：第4种积木和第5种积木难道不是一种吗？确实不是，在游戏屏幕里，积木是不允许左右翻转或者上下翻转的，每次旋转只能顺时针或逆时针旋转90°，第4种积木和第5种积木虽然是镜像关系，但其中一个不管旋转几次，都无法变成另外一个．所以，这其实是两种不同的积木．类似地，最后的两种积木，它们也算作不同的积木，不过，前面三种积木为什么没有镜像版本呢？原因很简单：前三种积木本身就是轴对称的，所以它们不“畏惧”旋转．

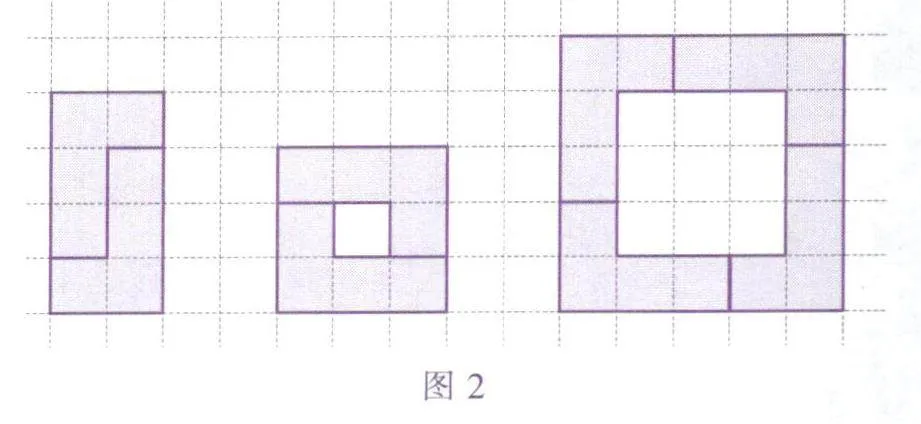
虽然其中四种积木本身并不是轴对称图形，但利用它们很容易拼出轴对称图形，以第4种积木为例，如果我们手中有很多块这种形状的积木，就可以拼出图2中的这些轴对称图形．

这并不令人感到惊讶，虽然这种形状的积木并不对称，但偶数个这样的积木可以对称地摆放，出现对称性也是理所当然的事情，

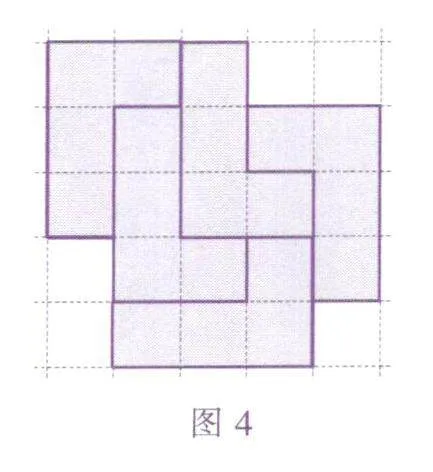
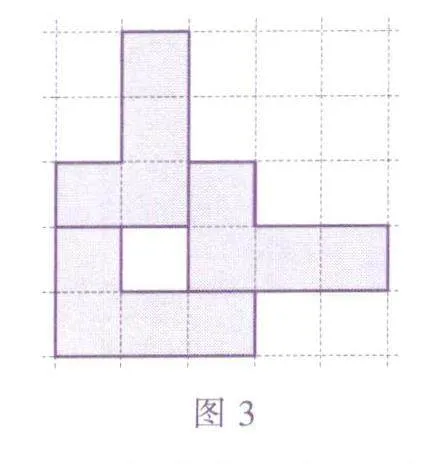
能不能用奇数个这样的积木拼出一个轴对称图形呢？答案仍然是肯定的，我们可以分别用3块和5块积木拼成下面的图形（图3和图4）．

你或许注意到了，这种用奇数个L形积木搭出的轴对称图形，对称轴都是沿着小正方形对角线方向的，是45°倾斜的直线，能否用奇数个这样的积木拼出一个左右对称或上下对称的图形呢？可以证明，这是永远办不到的．

假设我们要把若干个L形积木放进正方形网格里，组成一个左右对称的图形，它的对称轴位置有两种情况：穿过其中一列正方形的中心，以及正好和某根竖直的网格线重合．

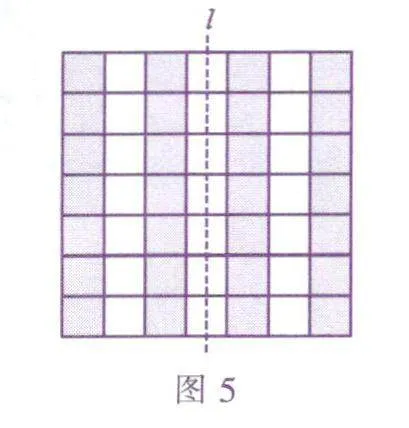
如果是前一种情况，那就把各列正方形交替染成黑白二色，使得这条对称轴穿过的正好是一列白色正方形（如图5）．由于整个图形关于对称轴左右对称，因此左半部分覆盖了多少个黑色小正方形，右半部分也会覆盖同样多个黑色小正方形．这说明，整个图形覆盖的黑色小正方形的个数为偶数．

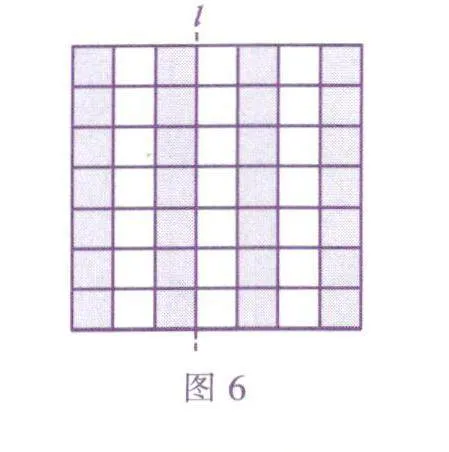
如果是后一种情况呢？同样把各列正方形交替染成黑白二色（如图6）．由于整个图形关于对称轴左右对称，因此左半部分每覆盖一个黑色小正方形，右半部分就会对应地覆盖一个白色小正方形；类似地，左半部分每覆盖一个白色小正方形，右半部分也就会对应地覆盖一个黑色小正方形．这说明，整个图形覆盖的黑白小正方形的个数相同，由于整个图形是由若干个L形积木组成的，每个积木包含4个小正方形，因此整个图形覆盖的小正方形总数是4的倍数．黑色小正方形占其中的一半，因而有偶数个．

然而，这两个网格里的任何一个L形积木，总会覆盖奇数个黑色小正方形，因此，要想让整个图形覆盖偶数个黑色小正方形，L形积木也得有偶数个，这就证明了，奇数个L形积木无法形成一个左右对称的图形．根据同样的道理，奇数个L形积木也无法形成一个上下对称的图形．