再议轴对称

许多剪纸作品都是对称图案，例如，沿“双鹊登枝图”（图1）正中的虚线将其对折，左右两边的图案会完全重合，它的剪法通常是先把一张纸对折，在折痕左边剪出如图2所示的图案，再把这张纸翻开铺平就得到完整的图案．像这样的图案，被称为左右对称，又如，沿“天鹅戏水图”（图3）正中的虚线将其对折，则上下两边的图案（天鹅与其倒影）会完全重合，像这样的图案，被称为上下对称．

上下对称和左右对称都属于图形对称中的同一种类型——轴对称，下面说说关于轴对称的几个基本概念，由此加深对轴对称的认识．

一、两点的轴对称

每个图形都是由无数个点集合而成的，我们先从点的轴对称说起，在一张纸上任意画出两个点，你能把这张纸折叠一次使这两点重合吗？请你试一试，如果试成了，将纸铺平，观察这两点与折痕的位置关系，你会发现：这两点分别在折痕的两边，而且折痕垂直平分连接这两点的线段，即折痕在这条线段的垂直平分线上．

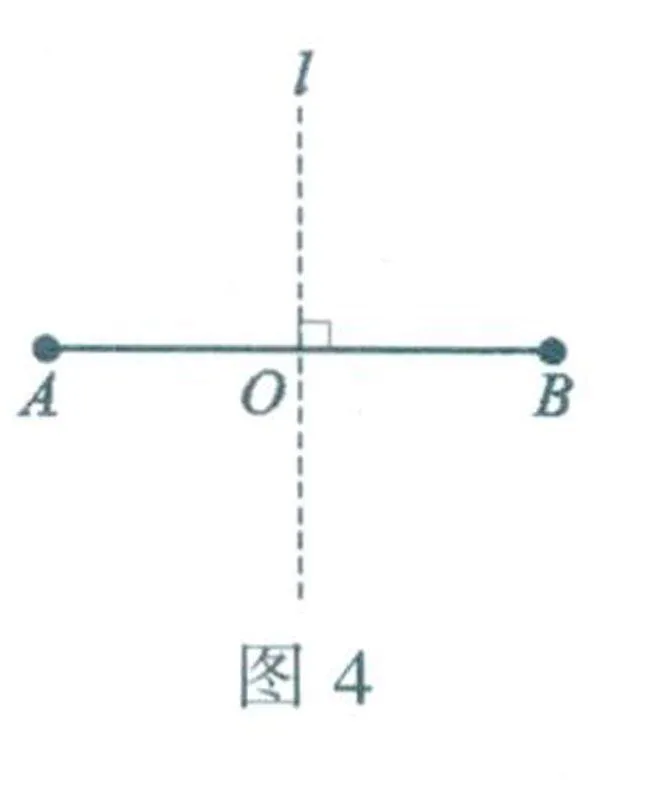
如图4，设平面上有两点A和B，如果直线l是线段AB的垂直平分线，则称点A和点B关于直线l对称，或者说点A和点B成轴对称，直线l是它们的对称轴，例如，图1中左右两只喜鹊的上喙尖是成轴对称的两点，对称轴是正中竖直虚线所在的直线，图3中天鹅与其倒影的两尾尖是成轴对称的两点，对称轴是正中水平虚线所在的直线．

平面上任意两点都是成轴对称的，它们有且仅有一条对称轴．两点的对称轴把平面分为两部分，每一部分称为半平面，这两点分别在两个半平面上，如果把其中一个半平面沿对称轴翻转180°，则随着两个半平面重合，这两点也一定重合．

如图5，在平面直角坐标系中，点A（2，1）和点B（-2，1）的对称轴是y轴，点A（2，1）和点C（2，-1）的对称轴是x轴，点A（2，1）和点D（1，2）的对称轴是过原点并且平分∠xOy的直线l．想一想：点（a，b）关于x轴和y轴的对称点分别是什么？

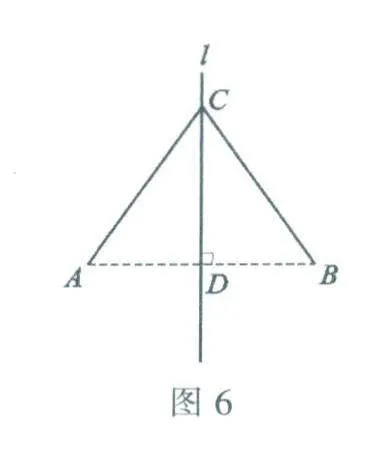
如下页图6，平面上两点A，B的对称轴l与线段AB交于点D．在l上任取一点C，连接线段AC与BC，则一定会有AC=BC，∠ACD=∠BCD.同学们可以利用全等三角形证明这个结论．

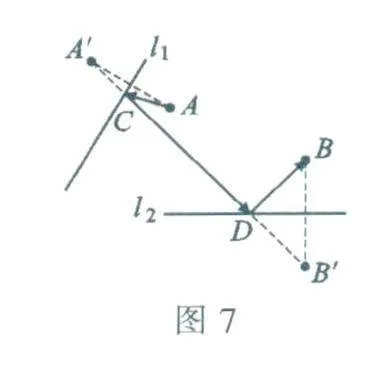
“最短路线”问题的解法也用到了两点的轴对称，如图7，一个人要从A地到直马路l1的路边送货，再到直马路l2的路边接货，并把接到的货送到B地，下面为他设计做完这些事的最短路线.A和B是定点，l1和l2是定直线，送货点C和接货点0分别是l1和l2上的动点，问题是：点C和点D选在何处做完事的路线最短？答案是：取点A关于直线l1的对称点A'，点B关于直线l2的对称点B'，连接A'，B'，线段A'B'与l1，l2分别交于点C和点0，折线ACDB即为最短路线，你能解释为什么这样做吗？

二、两个图形的轴对称

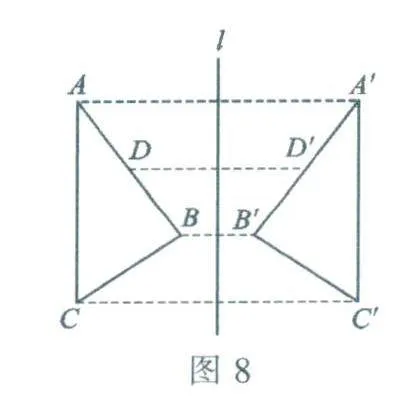
如图8，△ABC和△A'B'C'上的点可以一一对应，如点A对应点A'，点B对应点B'，点C对应点C'，点D对应点D，……并且每对对应点都关于同一直线l对称，即l是线段AA'，BB'，CC'，DD'等共有的垂直平分线．如果把图形沿l对折，则这两个三角形重合．

一般地说，如果两个图形上所有的点可以一一对应，并且每对对应点都关于同一直线对称，则称这两个图形关于这条直线对称，或者说这两个图形成轴对称，这条直线是它们的对称轴．例如，图8中△ABC和△A'B'C'是成轴对称的两个图形，直线l是它们的对称轴．

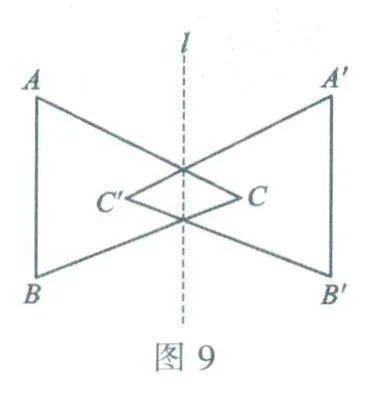
两个图形成轴对称，可能它们各自完整地分布在对称轴两侧，如图8；也可能每个图形都被对称轴分为两部分，如图9中△ABC和△A'B'C'的对称轴l穿过每个三角形．

在同一平面内，如果两个图形成轴对称，则对称轴把这个平面分为两个半平面，把其中一个半平面沿对称轴翻转180°，则原来两个图形一定重合．由此可知，成轴对称的两个图形一定全等．

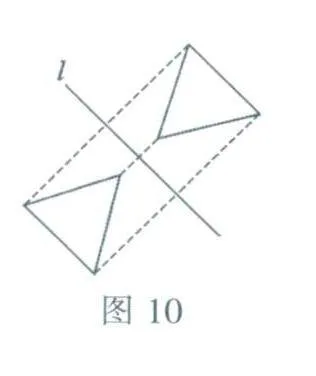
两个图形成轴对称有上下对称、左右对称，此外还包括其他情形，例如，图10中两个三角形关于斜线l成轴对称．

三、轴对称图形

一般地说，如果一个图形被一条直线分为两部分，这两部分图形关于这条直线对称，则这整个图形叫作轴对称图形，这条直线就是其对称轴．

轴对称图形的任何一条对称轴，都把它分为全等的两部分．你能找出图11中窗花的所有对称轴吗？

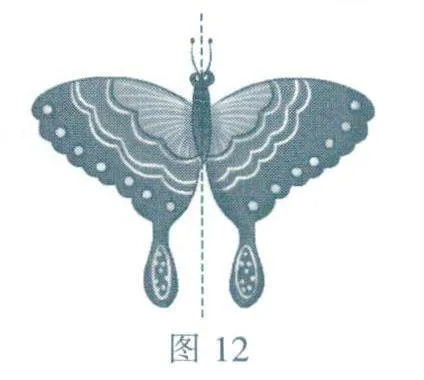
轴对称图形是对一个图形整体而言的，它内部包含成轴对称的两部分，它们的公共部分在对称轴上．例如，下页图12中的蝴蝶风筝是一个轴对称图形，对称轴把它分为左右对称的两部分，对称轴上的点为两部分共有，正因为风筝是轴对称图形，它才能平稳地飞行．同理，飞机的造型也是轴对称的（图13）．

由上可知，把一个轴对称图形沿对称轴一分为二，则得到成轴对称的两个图形．反之，把成轴对称的两个图形看作一个整体．则得到一个轴对称图形．

图形的轴对称能给人以美感，著名建筑学家梁思成说：“中国建筑的传统之一，是对中轴对称线的钟爱与恪守，”北京紫禁城（故宫）是中国建筑的典型代表，它的整体布局和宫殿造型都体现了轴对称（图14）．

四、轴对称变换

把一个图形按照某种方式变化为一个新图形，叫作图形的变换，例如，把图形G中的每一点按照同一方向移动同一距离，得到新图形C'，这就是平移变换，如果把图形G中的每一点都反射到关于同一条直线的对称点，得出的这些点又构成一个新图形G＂，这就是轴对称变换．

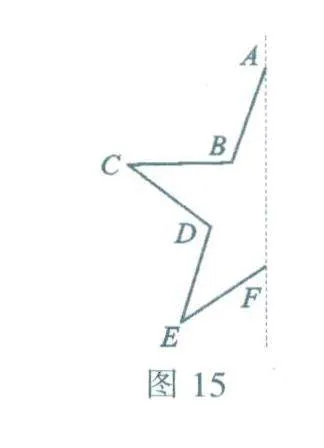
对有些图形实施轴对称变换时，可以只针对一些关键点进行操作，图15是一个五角星的左半部分，如要补画出完整的五角星，则可以直线AF为对称轴，把左半部分的点B，C，D，E作为关键点，进行轴对称变换．

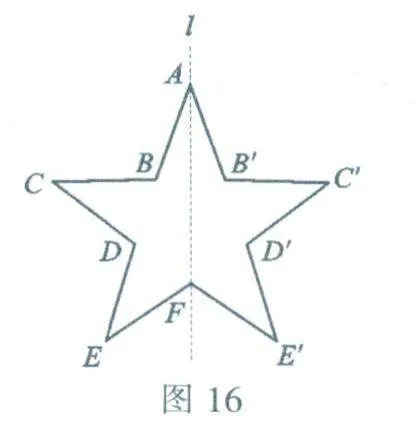
如图16．依次得出对称点B'，C'，D'，E'，再顺次连接AB'．B'C'．C'D'．D'E'，E'F，便得到了完整的五角星．

轴对称变换不仅可用于作图，还可用于证明和计算，

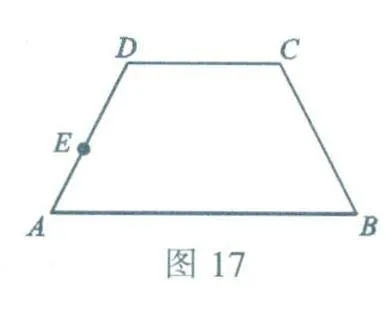
例 如图17，四边形ABCD中，AB∥CD，∠A=∠B.点E在AD上，AE：ED=m：n.试在BC上找出点F，使BFFC=m：n.

分析：本题很容易找出点F的位置，但要证明解法的合理性，就需以轴对称变换为依据．

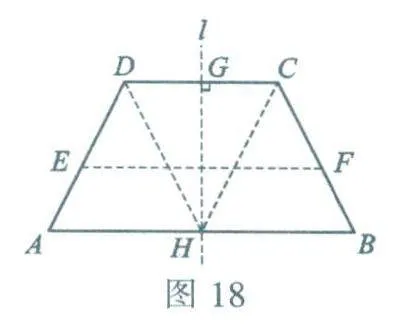
解：如图18，过点E作EF∥CD，EF交BC于点F，则BF：FC=m：n.下面证明这种解法的合理性．

作CD的垂直平分线l，分别交CD，AB于点G，H．连接CH，DH，则CH=DH，于是∠HDC=∠HCD.又AB∥CD，故∠HDC=∠AHD，∠HCD=∠BHC、于是∠AHD=∠BHC.又∠A=∠B，故△AHD≌△BHC（AAS），于是AH=BH.又l⊥AB，故l是AB的垂直平分线，因此，点A与点B关于l对称，又点D与点C关于l对称，所以线段AD与BC关于l对称，因轴对称变换不改变图形的形状和大小，故AD=BC.与以上推理相同，可知点E与点F关于l对称，BF=AE，FC=ED.又A E：ED=m：n，故BFFC=m：n.