基于门限自回归模型对人民币汇率波动的研究

摘 要：人民币汇率的波动受多方面因素的影响，为研究人民币汇率的波动情况，进一步预测人民币汇率的变化，本文以2011年1月—2023年12月的人民币兑美元的汇率中间价的月度数据作为研究对象，分别建立了求和自回归滑动平均模型和门限自回归模型，并对两种模型的预测结果进行对比。结果表明：人民币汇率的波动具有非线性特征，并且门限自回归模型比求和自回归滑动平均模型准确度更高，在未来几个月人民币兑美元中间价略有下降，但能够维持在相对稳定水平，人民币略有升值。

关键词：求和自回归滑动平均模型；门限自回归模型；人民币汇率；股份指数；ARIMA模型

中图分类号：F822；F037.1 文献标识码：A 文章编号：2096-0298（2024）12（a）--06

在日常生活中，以时间为一个序列，通过利用事物发展的延续性，结合已有数据，可以预测事物将会发生的趋势。最早开始兴起的是线性自回归（AR）模型，但随着研究的深入，人们发现自回归模型在处理一些实际问题时具有局限性，大量宏观经济序列存在非线性动态调整的特征，在经济预测中，增长率、通货膨胀率、失业率等在不同商业周期呈现出不同的动态调整机制[1]，在资产定价中，股票价格、汇率、利率等金融时间序列均具有非线性的特点，这时使用自回归模型进行建模不再合适。

把ARMA模型推广到允许其AR多项式以1作为特征根，则模型变成求和自回归滑动平均模型。求和自回归滑动平均模型（Autoregressive Integrated Moving Average Model，简称ARIMA模型）是一种单位根非平稳的模型，惯用的方法是对其进行差分化处理，使其变为平稳的时间序列模型，进一步可应用ARMA模型研究其相应性质。

门限自回归模型（Threshold Autoregressive Model，TAR）是一种非线性模型[2]，最初由H. Tong和Lim在1978年提出[3]，旨在处理具有明显非线性特征的时间序列数据，其思路是将非线性的时间序列划分成多个区间，在每个区间内建立线性的自回归模型，利用门限的控制作用，保证了模型的稳定性和广泛适用性，与多元线性回归、模糊分析、灰色模型等预测模型相比，门限自回归模型更具有稳定性和适用性[3]。

门限自回归模型广泛应用于多个领域，在经济预测方面，有刘玉凤等（2014）[4]、石自忠等（2014）[5]所研究的牛肉与羊肉的价格预测，利用两门限自回归模型对价格同比指数序列进行分析；在资产定价中，有周连强（2016）[6]以上海股票市场和深圳股票市场的每日收盘指数作为研究对象，探讨两种股份指数序列的非线性特征；同时，在汇率的非线性研究中，刘谭秋（2007）[7]利用线性的自我激励阈值自回归模型拟合人民币实际汇率历史数据，靳晓婷等（2008）[8]利用不同时间段汇率数据建立了门限自回归模型，得出结论：2005年7月—2008年1月的人民币汇率波动存在非线性特征。

汇率的波动会通过作用进出口商品的价格，通过各种途径影响到居民的消费行为，汇率的短期预测对国家出台相关货币政策、财政政策均具有重要意义，对企业的进出口、投融资具有指导价值。

在对人民币汇率波动的研究中，钟大勇和张恒（2021）[9]采用广义自回归条件异方差GARCH模型对人民币汇率的波动进行研究，李明轩和俞翰君（2020）[10]采用自回归滑动平均ARMA模型与GARCH模型、EGARCH模型、TGARCH模型和GARCH-M模型对数据的波动性进行研究；王艺柳（2024）[11]将求和自回归滑动平均ARIMA模型与广义自回归条件异方差GARCH模型进行组合建模，改良了ARIMA模型的预测准确度；康宁，刘霆（2022）[12]通过建立门限分位数自回归TQAR模型深入研究人民币汇率的波动情况，研究结果表明人民币汇率具有两阶段的非线性特征，同时呈现典型的异质性；苏玉华（2012）[13]比较了TAR模型、ARIMA模型及GARCH模型对人民币汇率预测的准确度，认为TAR模型更具优势。

本文以2011年1月—2023年12月的人民币兑美元的汇率中间价作为研究对象。首先，介绍ARIMA模型和TAR模型的相关理论知识；其次，分别应用ARIMA模型和TAR模型对取对数后的汇率中间价进行建模和预测；再次，比较ARIMA模型与TAR模型的预测结果，选出TAR模型作为最终应用模型；最后，根据预测结果，给出相应的分析结果与建议。

1 理论基础

1.1 ARIMA模型

ARIMA模型作为一种基本平稳时间序列模型得到了广泛应用。但现实问题中，观测序列{Xt}可能不是平稳序列，此时不能应用ARMA模型进行建模，需对模型进行平稳化处理。序列差分后变为平稳的时间序列，差分后的序列则可应用ARMA模型进行建模。此时原序列则为ARIMA模型。

求和自回归滑动平均模型（Autoregressive Integrated Moving Average Model），简称ARIMA模型，结合了AR模型与MA模型，可以更好捕捉到变化趋势。该模型可表示为：

并记为ARIMA（p，d，q），其中c为常数项，d，ai，bj是差分阶数，AR模型和MA模型的参数，εt为误差项。

ARIMA模型建模流程：第一步，对序列进行平稳性检验和白噪声检验，如果序列非平稳，但经过差分后序列平稳且非白噪声，则进行下一步，此步可以确定ARIMA模型中的未知量d；第二步，通过观察自相关系数图和偏自相关系数图进行模型识别和参数估计；第三步，对构造的模型进行检验；第四步，根据构造模型进行模型预测。

1.2 TAR模型

为限自回归模型[14]，并记为TAR（l，d;τ1，…τi-1;p1，p2，…，pl）中τj， j=1，2，…，l-1限值，l为门限区间的个数，d为延迟步数。a0（j），pj分别为第j个门限区间的内自回归模型的系数和阶数。

在建立TAR模型前首先需要进行非线性检验，其基本思想是：在线性假设下，一个合适确立的线性模型的残差应该是独立的，任何对残差独立性的违背都说明现有模型包括线性的假设不合适[15]。

建立TAR模型的关键在于确定门限区间的个数l、门限值τ1，τ2，…，τl-1迟步数d，通过对门限个数l，门限值τ1，τ2，…，τl-1迟步数d寻优确定模型参数。

1.3 三类常见的门限自回归模型

常见门限自回归模型（TAR）有单门限、双门限和三门限模型。

1.3.1 单门限自回归模型

单门限自回归模型即l=2，门限值为τ1，由于不同门限区间可能有不同的自回归系数和阶数，故a0（1），p1记为第1个门限区间内的系数和阶数，a0（2），p2记为第2个门限区间内的系数和阶数，故单门限自回归模型可以表示为

1.3.2 双门限自回归模型

双门限自回归模型，即l=3，门限值为τ1，τ2，双门限自回归模型可以表示为

1.3.3 三门限自回归模型

三门限自回归模型，即l=4，门限值为τ1，τ2，τ3，三门限自回归模型可以表示为

在实际应用中，建立门限自回归模型时，门限个数往往选择1个、2个或3个，因为门限个数越多越复杂，越容易导致过拟合现象，在理论部分不限制门限个数。本文实证分析部分考虑用单门限自回归模型对相应数据进行建模和预测。

2 实证分析

2.1 数据来源

人民币汇率中间价的变动情况，尤其是对美元的汇率中间价，是观察人民币汇率走势的重要指标。本文实证分析使用国家外汇管理局给出的数据，标价方法为直接标价法，其含义为100美元所兑人民币数量。这个价格对于指导市场预期、影响外汇交易及宏观经济政策都有重要作用。

数据样本选择2011年1月—2023年12月的人民币兑美元的汇率中间价的月平均值{Xt}建模数据，为减少数据波动，对数据全部采取对数化处理，生成新的数据 {lnXt}。

2.2 建立ARIMA模型

建立ARIMA模型之前，首先需对模型进行平稳性检验。

2.2.1 平稳性检验

平稳性检验的方法包括时序图判别法、自相关系数检验法、分段检验法、单位根检验法等。本文只介绍自相关系数检验法。自相关系数检验法的原理是：平稳的时间序列是具有短期相关性的，其自相关系数表现为截尾、拖尾的情形，即自相关系数会随着延迟期数的增加快速的变为零或以指数形式向零衰减。

序列的自相关系数图随着滞后阶数的增加快速下降为0，该序列为平稳序列（此处省略了其自相关系数图）。

2.2.2 模型建立

本文利用EViews10软件，对ARIMA模型进行定阶，得到ARIMA（1，0，1）到ARIMA（19，0，1）共38个建模结果，通过比较每个模型对应的AIC值，得到最优模型为ARIMA（1，0，1），也就是模型估计为

lnXt=0.112+0.983lnXt-1+0.456εt-1（6）

TAR模型为本文主要考虑的模型，此部分省略了ARIMA模型的模型检验与模型预测部分，感兴趣的读者可自行进行检验和预测。

2.3 建立TAR模型

2.3.1 非线性检验

门限自回归模型适用于非线性的时间序列，故在建模前，对时间序列进行非线性检验，以保证该序列适用门限自回归模型。非线性检验包括参数和非参数统计量。非线性检验的基本思想是：在线性假设下，一个合适确立的线性模型的残差应该是独立的，任何对残差独立性的违背都说明现有模型包括线性的假设不合适，所以通过观察残差、残差平方和的自相关系数图和偏自相关系数图可以确定残差序列是否具有非线性特征，在显著性水平为α=0.05，如果P值小于0.05则认为残差序列具有自相关性，即存在非线性特征。

通过观察时间序列图有助于发现时间序列的非线性特征，也可通过观察现有模型的残差和残差平方和的自相关系数图和偏自相关系数图判断是否具有非线性特征。这里对于通过时间序列图观测非线性特征部分不做赘述。

本文尝试对时间序列建立AR（2）模型，通过观察AR（2）模型的残差和残差平方和的自相关系数图和偏自相关系数图（图1、图2）可以看出存在P<0.05，即残差之间存在自相关，故该序列具有非线性特征。

2.3.2 模型建立

建立TAR模型的关键在于确定门限区间的个数l、门限值τ1，τ2，…τl-1迟步数d，这是对门限个数l，门限值τ1，τ2，…τl-1迟步数d的寻优过程。在每个门限区间，还需确定AR模型的阶数p1，p2，…pl数寻优时，可采用AIC准则来选择模型阶数和最优参数。因此，AIC是所有2l+1个参数的函数，即

AIC=f （p1，p2，…，pl，l，d，τ1，τ2，…τl-1）（7）

使AIC值达到最小参数，即最终的TAR模型的参数。

对于确定的时间序列{Xt，t=1，…，N}AR模型的常用参数估计方法具体步骤如下所示[14]：

（1）确定区间个数l、延迟步数d和每个区间AR模型阶数p1，p2，…pl界L，D和P。其中，p1，p2，…pl每个pj的上界均可以不同，但为了方便起见，选择公共的上界P，并且所确定区间个数一般为1～3个，即L不超过3。

（2）给出门限值τ1，τ2，…τl-1值，由于门限值的确定过程是逐步寻优过程，可将已有的时间序列取值从小到大排列，分别取0.3n，0.4n，0.5n，0.6n，0.7n所对应的值为门限值，从而确定（-∞，+∞）的剖分{Ωj}。

（3）把序列{Xt，t=1，…，N}按照Xt-d落在剖分{Ωj}中的情况分为l组。

（4）对于落在第j（1≤j≤l）个区间内的序列，建立AR模型如下：

分别令其阶数pj取值从1增大到P，可以得到AR模型的参数ai（j）， j=0，1，…，pj机误差εt（j）的方差、AIC值，令AIC为P个AIC值中的最小值，相应的区间的AR模型的阶数，从而得到每个区间适用的AR模型。

对于落在第j（1≤j≤l）个区间内AR模型的参数可由最小二乘法、矩估计和最大似然估计方法得到。

（5）各区间确定最小AIC值为AIC可以得到整个时间序列模型的最小AIC值之和为：

（6）对门限值寻优：固定门限个数l和延迟步数d，按照迭代算法对确定的门限值τ1，τ2，…τl-1，每次迭代时，重复步骤3～5，并计算模型的AIC值，使得AIC值达到最小的参数值为给定l和d时的估计值，相应AIC值记为。

（7）对延迟步数寻优：固定门限个数l，让d从1增大到D，重复步骤3～6，使得最小的d即为估计值应的AIC值记为。

（8）对门限个数寻优：让l从2增大到L，重复步骤3～7，使得最小的l，即为估计值而得到每个参数的估计值。

在上述估计过程中，依次估计模型的不同参数，即先确定门限值τ1，τ2，…τl-1的估计值给定的情况下再确定延迟步数d的估计值后确定门限个数l的最佳取值。

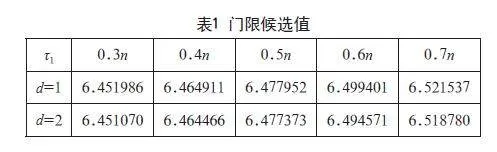
本文考虑对建立单门限自回归模型，即门限区间个数为l=2，即门限值个数为1，延迟步数上界D=2，每个区间AR模型的阶数上界P=3。将样本数据从小到大进行排列，分别选择0.3n、0.4n、0.5n、0.6n、0.7n所对应的值作为门限候选值τ1，对于每一个确定的延迟步数，均可以得到5个门限值，如表1所示。

利用延迟步数d=1和d=2时的10个门限值分别确定剖分{Ωj}， 把序列{Xt，t=1，…，N}按Xt-1和Xt-2落在剖分{Ωj}中的情况分为2组，对以上区间的数据分别建立AR（1），AR（2），AR（3）模型，可以得到AR模型的表达式，并计算AIC值。

通过迭代法，延迟步数d=1时，最优门限值为τ1=6.464911，此时AIC（2，1，6.464911），AIC（2）=-543.170；延迟步数d=2固定时，最优门限值为τ1=6.45107时AIC（2，2，6.45107）=-944.866，AIC（1）=-334.636，AIC（2）=-610.230。

因为AIC（2，1，6.464911）<AIC（2，2，6.45107）最优延迟步数为d=1，最优门限值为τ1=6.464911，得到预测方程：

2.3.3 模型检验

模型的检验包括两种：

（1）对模型的有效性进行检验。合适的拟合模型应该能提取观测序列几乎所有样本的信息，即残差序列应为白噪声序列。

（2）对参数的显著性进行检验。对于参数aj的检验，其原假设和备择假设分别为，检验统计量为：

在给定的显著水平α下，如果P<α，则可以1-α的置信水平拒绝原假设，认为该模型参数显著；反之则该模型不显著。

2.4 模型预测

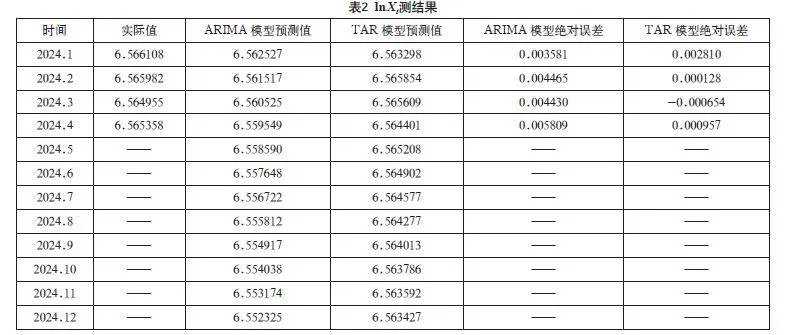
根据以上得出的ARIMA模型（1）和单门限自回归模型（2），可以得到预测结果（表2）。

由表2可得两个模型的预测结果，并得到ARIMA模型的平均绝对误差值为0.004571，TAR模型的平均绝对误差值为0.003241，TAR模型的预测准确性更高。

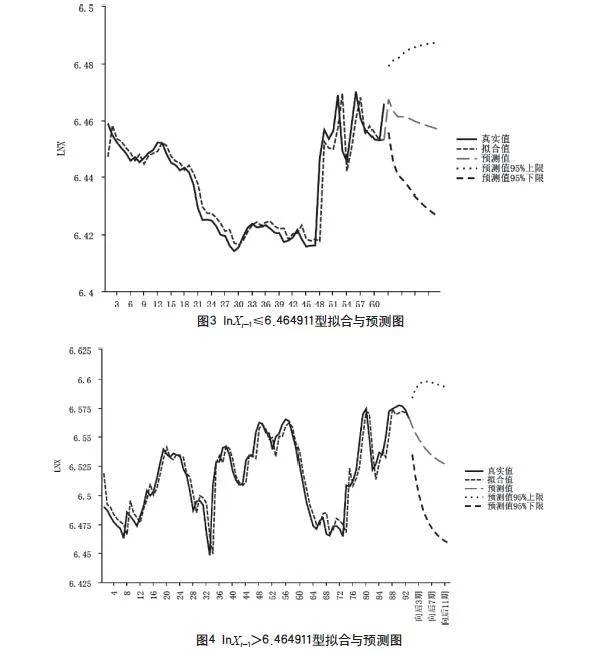
根据式（2）给出了模型的预测方程，可以得到模型的拟合与预测图，当lnXt-1≤6.464911合图为图4，当lnXt-1> 6.464911合图为图5。

通过图3和图4可以看出，预测值和实际值拟合效果较好，通过表2可以看出，预测值的绝对误差较小，说明该预测模型比较合适。

通过表2预测结果可以看到，2024年5月人民币兑美元中间价为709.959552，6月人民币兑美元中间价为709.742338，7月人民币兑美元中间价为709.511709，8月人民币兑美元中间价为709.299889。从短期来看，人民币兑美元中间价较2024年初有所下降，人民币升值，但整体维持在相对稳定的水平，更有利于中国的经济和金融市场的稳定发展。

3 结语

本文基于门限自回归模型的基本理论，研究了人民币汇率的波动预测模型，汇率的波动会通过作用进出口商品的价格，通过各种途径影响到居民的消费行为[16]，预测人民币汇率的波动并及时做出相应政策调整，有利于企业和国家的进一步发展。

通过对人民币汇率的研究表明，在未来3个月，人民币兑美元中间价略有下降，但将继续稳定在合理均衡水平，人民币略有升值。有相关专家认为这归因于以下三个方面[17]：首先，2023年12月以来，通货膨胀压力减轻，全球多国央行停止加息，开启降息周期，美元指数或继续回落，人民币升值；其次，美国经济显现出韧性，中美货币政策仍存在一定程度的错位；最后，人民币汇率中间价逆周期因子释放信号，当前在岸及离岸汇率较人民币中间价偏离幅度较大，中间价或在美元强势之下被动调整。

人民币汇率变化首先对进出口的影响最大，人民币升值，对于等值的外币会兑换更少的人民币，相关文献[18]认为人民币升值会抑制我国企业的出口。其次，货币政策也会随着人民币汇率的变化而改变，人民币升值，货币政策将延续强化逆周期和跨周期调节思路，继续加大对实体经济的支持，刺激消费、扩大内需[19]。人民币升值还有利于扩大国内群众对进口产品的需求、增加居民消费的多样性，减轻企业进口的成本，同时会对出口企业产生不良影响，有利于“倒逼”国内企业产业结构转型升级。

参考文献

聂思玥.门限自回归模型的理论与应用研究[D].南京：南开大学，2014.

孟庆斌，周爱民，靳晓婷.基于TAR模型的中国股市价格泡沫检验[J].南开经济研究，2008（4）：46-55.

张亮.门限自回归（TAR）模型及其在汇率波动问题中的研究[D].芜湖：安徽工程大学，2013.

刘玉凤，王明利，石自忠.基于门限自回归的我国羊肉价格波动分析[J].广东农业科学，2014，41（17）：206-210.

石自忠，王明利，胡向东.我国牛肉价格波动的门限及政策研究[J].中国农业大学学报，2014，19（4）：200-205.

周连强.TAR模型在沪深股票市场研究中的应用[J].商业时代，2010（21）：72-73.

刘潭秋.人民币实际汇率的非线性特征研究[J].数量经济技术经济研究，2007（2）：11-18.

靳晓婷，张晓峒，栾惠德.汇改后人民币汇率波动的非线性特征研究： 基于门限自回归TAR模型[J].财经研究，2008，34（9）：48-57.

钟大勇，张恒.基于GARCH模型的人民币汇率波动研究[J].中国物价，2021（10）：24-26.

李明轩，俞翰君.基于ARMA—GARCH模型的人民币汇率波动性研究[J].时代金融，2020（33）：1-3+8.

王艺柳.基于ARIMA-GARCH模型的人民币汇率波动研究[J].中国商论，2024（11）：9-12.

康宁，刘霆.基于门限分位数自回归模型的人民币汇率波动及预测研究[J].阜阳师范大学学报（自然科学版），2022，39（2）：24-32.

苏玉华.人民币汇率预测模型与实证研究[J].时代金融，2012（26）：11-12.

周永道，王会琦，吕王勇.时间序列分析及应用[M].北京：高等教育出版社，2015.

Ruey S. Tsay.王辉，潘家柱.金融时间序列分析（第二版）[M].北京：人民邮电出版社，2009.

王姝睿.[2024年汇市展望]人民币汇率2023年“先抑后扬”2024年有望继续升值[Z].https：//finance.sina.com.cn/money/forex/rmb/2024-01-03/doc-inaafauh4685461.shtml，2024-1-3.

姚进.人民币汇率保持基本稳定有坚实基础[N].经济日报，2024-3-28（11）.

金朝辉，朱孟楠.人民币实际汇率变动对出口贸易的影响[J].国际贸易问题，2021（5）：143-160.

温彬，张丽云，韩思达，等.关注央行的“新提法”： 2024年一季度货币政策执行报告解读[Z].https：//finance.sina.com.cn/jjxw/2024-05-14/doc-inavestp4338313.shtml，2024-5-14.