城轨交通下不同扣件参数对钢弹簧浮置板振动响应影响研究

摘 要：钢弹簧浮置板轨道具有较好的结构稳定性，能够承受地铁列车的运行冲击和乘客的集中载荷，确保地铁站台的安全性和稳定性。文章以常见的地铁B型车及钢弹簧浮置板轨道为例，基于有限元仿真模型与多体动力学仿真模型，根据扣件不同参数工况下，对浮置板的振动响应进行了仿真分析。结果表明：扣件刚度对轨道系统的振动影响非常大，扣件刚度过小会影响轮轨系统的稳定性和安全性。通过增加扣件的阻尼，可以减少振动的幅值和能量，从而降低浮置板轨道的加速度响应，提高系统的稳定性和舒适性。

关键词：轨道车辆；钢弹簧浮置板；有限元仿真；扣件

中图分类号：F259；U270.33 文献标志码：A DOI：10.13714/j.cnki.1002-3100.2024.20.025

Abstract： The steel spring floating plate track has good structural stability， which can withstand the impact of subway train operation and the concentrated load of passengers to ensure the safety and stability of subway platforms. This paper takes the common subway B-type car and steel spring floating plate track as an example， based on the finite element simulation model and multi-body dynamics simulation model， according to the different parameters of fasteners under different working conditions， and the vibration response of the floating plate has been simulated and analyzed. The results show that the fastener stiffness has a great influence on the vibration of the rail system， and the stability and safety of the wheel-rail system may be affected if the fastener stiffness is too small. By increasing the damping of the fasteners， the amplitude and energy of the vibration can be reduced， thus reducing the acceleration response of the floating plate rail and improving the stability and comfort of the system.

Key words： rail vehicles; steel spring floating plates; finite element simulation; fasteners

0 引 言

随着我国城市轨道交通的迅速发展，环境和噪声问题成为了亟待解决的挑战之一[1]。浮置板轨道作为一种高效减振轨道类型，可以在一定程度上减少地铁运行所带来的振动和噪声[2-3]。

钢弹簧浮置板轨道的基本工作原理是通过将地铁轨道下方的弹簧系统与轨道上的浮置板结合，形成一个质量-弹簧隔振系统，以减少地铁列车行驶时产生的振动和噪音[4]。钢弹簧浮置板在对外减振的同时，可能会面临区段振动、噪音增强以及钢轨波形磨耗等问题，这些问题可能会对乘客的舒适度和列车运行的安全性产生不利影响。

为了抑制轨道板自身的振动，研究学者多从改变轨道系统的主要参数进行研究。丁德云等[5]通过建立有限元模型及正交实验，发现影响钢弹簧浮置板轨道低阶固有频率的主要参数是支承间距、道床板厚度和弹簧刚度；韦凯等[6]构建车辆与轨道系统相耦合的垂向模型，计算分析了钢弹簧的刚度和阻尼参数对浮置板中低频振动的影响；张宏亮[7]以北京地铁5号线与13号线铺设的钢弹簧浮置板轨道为研究对象，建立了多种动力学有限元模型，分析了浮置板轨道的力学特性。孙晓静等[8]基于ANSYS分析软件与振动理论，以Sperling指标为依据，研究了钢弹簧刚度和阻尼变化对乘车舒适性和地基反力的变化规律。本文基于有限元软件与多体动力学软件建立了城市轨道车辆-轨道耦合模型，旨在通过研究扣件不同刚度与阻尼条件下，钢弹簧浮置板轨道的振动响应，可为优化轨道结构参数，提高轨道结构稳定性提供参考。

1 车辆—轨道耦合模型建模方法

基于车辆-轨道耦合动力学理论，将有限元计算的刚度矩阵、质量矩阵等柔性体模态，通过模态分析法子结构缩减的方式导入到多体动力学软件中，从而进行车辆轨道耦合联合仿真分析，利于模拟更加真实的工况和符合实际工况的结果[9]。柔性轨道与车辆模型集成方法如图1所示，本文通过ABAQUS软件进行柔性钢轨与柔性浮置板的有限元模型建立，并通过软件接口导入到SIMPACK软件中，实现车辆轨道刚柔耦合。

2 车辆-轨道耦合模型建模

2.1 轨道车辆模型建模

本研究选取地铁B型车作为车辆模型，其部分参数如表1所示。由于地铁车辆系统较为复杂，尤其是耦合模型存在轮轨接触几何及轮轨蠕滑非线性等各种复杂的非线性环节，此处为了方便仿真计算，在保证精度的前提下，对整体结构做简化处理[10]。由图2整体拓扑图可知，整节列车主体由一个车体，两个转向架，四个轮对构成，均视为刚体，每个刚体都具有6个自由度。此外，一系弹簧与二系弹簧可采用软件的弹簧-阻尼单元进行模拟，抗侧滚扭杆，减震器采用非线性弹簧-阻尼单元进行模拟。轮轨力的计算方法选择FASTSIM理论。

2.2 钢弹簧浮置板轨道建模

钢弹簧浮置板轨道系统主要包括钢轨、扣件、浮置板、隔振器等结构。在有限元软件ABAQUS中，钢轨模型采用标准的UIC60轨，整体长度为21m，为了能够进行模态缩减，在钢轨轨顶处与轨底处分别建立主节点。扣件间距为0.6m。建立了3块浮置板，单块浮置板尺寸为3.576m×2.7m×0.37m，每块浮置板均由6个钢弹簧隔振器支撑，钢轨与浮置板均采用实体柔性单元创建，钢弹簧浮置板轨道参数如表2所示。在完成轨道模型建模后，对模型进行模态分析，并进行质量矩阵与刚度矩阵的计算，得到*.inp与*.sim结果文件，通过ABAQUS-SIMPACK接口，得到*.fbi文件，集成到SIMPACK软件中[11]，最终得到的车辆-轨道耦合模型如图3所示。

2.3 轨道不平顺

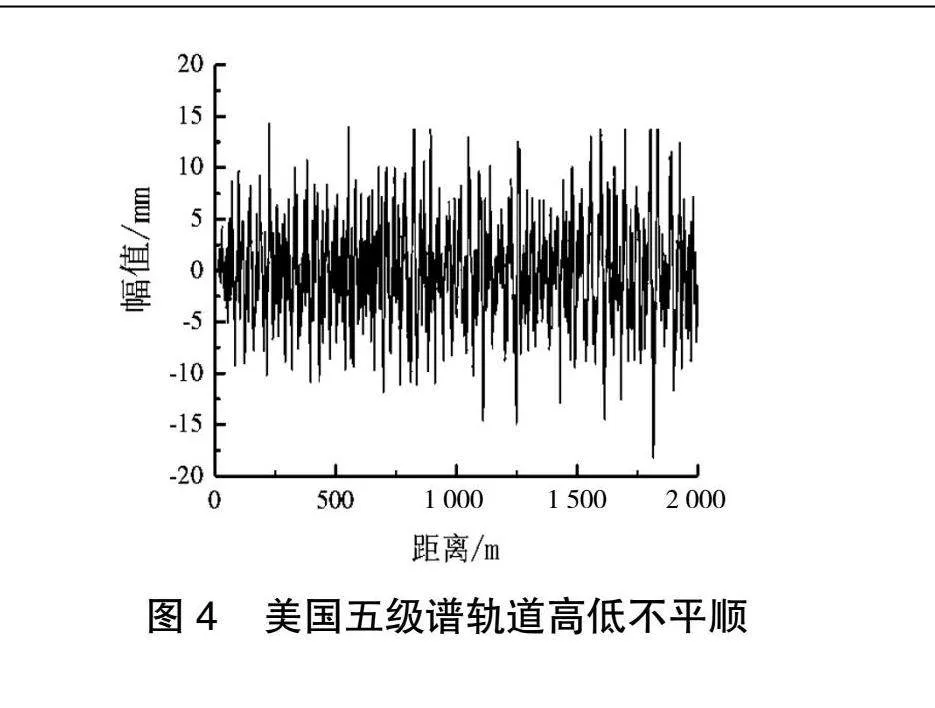
轨道不平顺是车辆运行过程中导致车体与轨道振动的主要激励源[12]。为了能够模拟真实的轨道运行情况，本文采用美国五级谱模拟轨道高低不平顺。美国谱中轨道高低不平顺的公式如下。

其中：Ω是不平顺空间角频率，单位为rad/m。

本研究在SIMPACK软件中采用功率谱密度（PSD）的方式，得到时域上的轨道高度不平顺激励，如图4所示。

3 仿真结果与分析

3.1 不同扣件刚度的影响

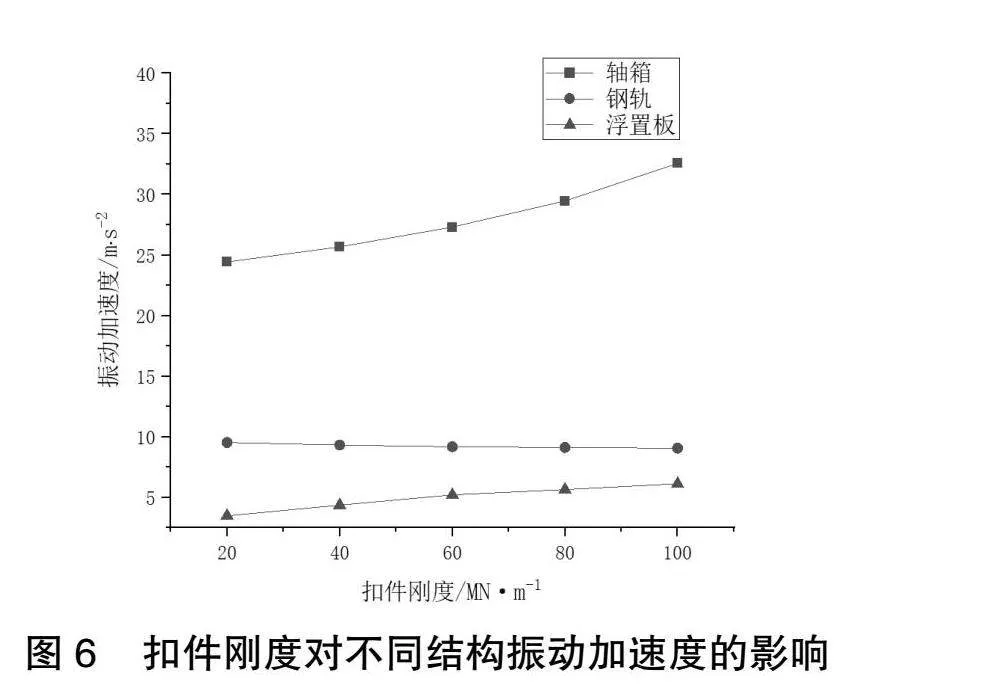
扣件的刚度决定了钢轨与浮置板之间的刚性连接程度，从而影响了力的传递效率、振动的传播方式以及系统的动态响应，因此，选择合适的扣件刚度对于确保系统的稳定性、高效性和安全性具有重要意义[13]。本次仿真实验车辆模拟速度为60km/h，仿真时间为1s，采样频率为10kHz。其中扣件刚度为20 MN·m-1，浮置板轨道的振动加速度仿真结果如图5所示，图6展示了扣件刚度五种工况下，轴箱，钢轨及浮置板轨道的振动加速度变化趋势。

由图6可以得出浮置板轨道振动响应随扣件刚度的变化规律。扣件刚度增大，浮置板与轴箱的振动加速度增大，钢轨的振动加速度变小，当扣件刚度到达60 MN·m-1后，浮置板轨道的振动加速度呈现减缓的趋势。扣件刚度增加可能会增加振动传播的能量，导致浮置板振动影响加剧，而扣件刚度过小则可能会影响轮轨系统的稳定性和安全性。因此，扣件刚度的设计需要进行合理权衡，以确保轮轨系统在运行时能够达到良好的动力学性能和安全性。因此，根据仿真工况，并考虑到运行安全，扣件刚度取 40～60 MN·m-1较为合适。

3.2 不同扣件阻尼的影响

在车辆移动载荷作用下，扣件阻尼参数的取值对车辆轨道系统响应具有重要影响。扣件阻尼的大小会影响轨道系统的振动衰减速度和稳定性[14]。扣件阻尼选择常规的五种工况进行仿真，仿真结果如图7所示。

由图8可知，随着扣件阻尼的增加，浮置板、轴箱、钢轨的振动加速度均有所下降，但轴箱振动加速度变化幅值较大。可以分析得出：通过增加扣件的阻尼，可以减少振动的幅值和能量，从而降低轮轨系统的加速度响应，提高系统的稳定性和舒适性。这意味着增加扣件阻尼并不会引起其他不利影响，这说明在实际应用中，增加扣件阻尼对其他系统参数的影响较小。因此，在实际工程中，应该尽量采用技术上允许的大阻尼扣件系统，以最大程度地提高轮轨系统的稳定性和乘坐舒适性，同时确保系统的安全性和可靠性[15]。

4 结 论

本文针对扣件不同参数对钢弹簧浮置板轨道振动响应进行了研究，通过有限元模型与多体动力学模型相结合的方式进行了仿真分析，得到以下结论：扣件刚度增加可能会增加轨道系统的振动，导致浮置板振动影响加剧，而扣件刚度过小则可能会影响轮轨系统的稳定性和安全性，因此，扣件刚度取40～60 MN·m-1较为合适。通过增加扣件的阻尼，可以减少振动的幅值和能量，能够降低轮轨系统的加速度响应，提高系统的稳定性和舒适性。

参考文献：

[1] 王文斌，刘力，孙宁．我国城市轨道交通轨道减振现状与发展趋势[J]．中国铁路，2013（4）：91-94.

[2] 王谊，何华凤，徐赞．城市轨道交通振动噪声治理技术研究综述[J]．城市轨道交通研究，2023，26（6）：216-219，224.

[3] 梁瑞华，马蒙，刘卫丰， 等．考虑地层动力特性差异的减振轨道减振效果评价[J]．工程力学，2020，37（S1）：75-81.

[4] 马蒙，李明航，吴宗臻，等．地铁列车与定点锤击荷载下浮置板轨道减振效果对比试验研究[J]．中国铁道科学，2019，40（5）：28-34.

[5] 丁德云，刘维宁，李克飞，等．钢弹簧浮置板轨道参数研究[J]．中国铁道科学，2011，32（1）：30-35.

[6] 韦凯，豆银玲，杨麒陆，等．钢弹簧浮置板轨道的随机振动分析及参数优化[J]．华中科技大学学报（自然科学版），2017，45（8）：115-119.

[7] 张宏亮．隧道内钢弹簧浮置板轨道结构振动特性及其对环境影响的研究[D]．北京：北京交通大学，2007.

[8] 孙晓静，李术才，张敦福，等．车辆-钢轨-钢弹簧浮置板道床耦合系统振动特性分析[J]．山东大学学报（工学版），2011，41 （3）：126-130，136.

[9] 杜浩洁．钢弹簧浮置板减振轨道的抑振研究[D]．兰州：兰州交通大学，2022.

[10] 高可．基于车-轨-浮置板耦合模型的车轴应力响应与浮置板振动特性分析[D]．石家庄：石家庄铁道大学，2023.

[11] 程珊．高架钢弹簧浮置板轨道减振特性分析[D]．南昌：华东交通大学，2018.

[12] 邢文佳．钢弹簧失能下车辆-浮置板轨道振动特性及检测研究[D]．石家庄：石家庄铁道大学，2023.

[13] 王刘翀，刘冬娅，易强，等．曲线地段钢弹簧浮置板轨道振动特性试验研究[J]．铁道科学与工程学报，2019，16（3）：610-619.

[14] 李明航，王文斌，李喆，等．随机轮轨动态激励对钢弹簧浮置板轨道减振性能影响分析[J]．工程力学，2024，41（S1）：292-299，345.

[15] 王文波，关庆华，温泽峰．车辆载荷下钢弹簧浮置板轨道振动特性分析[J]．噪声与振动控制，2024，44（1）：212-219.