ADDIE模型下培养高阶思维能力的单元教学设计与策略

【摘 要】高阶思维能力是一种以高层次认知水平为主的综合性思维能力。文章以初中数学人教A版“相似”为例，根据课程标准内容，基于ADDIE模型制订指向高阶思维培养的“相似”单元教学设计，包括教学内容分析、单元教学设计、单元整体教学设计评价等流程。并提出相应的教学策略，即设计单元教学关联，奠定高阶思维发展；关注单元整体构建，促进高阶思维发展；着眼单元变式教学，引导高阶思维生成。

【关键词】ADDIE模型 高阶思维能力 单元教学 “相似”

【中图分类号】G623.5 【文献标识码】A 【文章编号】1002-3275（2024）13-46-04

一、问题提出

《义务教育数学课程标准（2022年版）》（以下简称课程标准）提出，初中阶段核心素养主要表现为抽象能力、运算能力、几何直观、空间观念、推理能力、数据观念、模型观念、应用意识、创新意识。其中，运算能力、推理能力、模型观念、应用意识、创新意识等都指向高阶思维能力。高阶思维能力的提出体现了以学生为本的教育理念，对落实以核心素养为导向的课程目标具有举足轻重的作用，并且高阶思维正成为创新型人才必备的素质之一。

高阶思维能力指的是发生在较高认知水平层次上的心智活动或认知的能力，在教学目标分类中表现为分析、综合、评价、创造，由问题解决思维能力、创造思维能力、决策思维能力、批判思维能力构成［1］，集中体现了新时代对人才素质提出的更高要求。目前，如何在教学过程中促进学生高阶思维能力的形成与发展成为许多学者关注的一个重点。梁伟虹和熊应龙以数学综合性课程“宝贝市集”为例，以项目式学习的形式实施课程，让学生在调查、计算、推理、策划、实践、反思的过程中发展实践思维、创新思维、整体思维。［2］胡军等强调教学要从“教师提问”转变为“学生提问”，通过培养质疑的意识、创设开放的情境、运用提问的方法，培养学生数学问题提出能力，激发学生的高阶思维。［3］谭师龙以小学低段数学综合与实践课为例，以建构主义理论和具身认知理论为理论依据，构建关于教学流程和高阶思维的教学设计框架，并从情景观察、游戏探究、动作操作、任务调查四个方面设计教学过程。［4］方立新和刘新春采用问题驱动教学，通过设计层层递进的数学“问题链”并将其贯穿于高阶思维活动的全过程，促进学生理解、探究、反思、体验，逐步提高学生的高阶思维能力。［5］纵观上述研究，诸多学者从不同角度提出了培养高阶思维能力的教学建议和教学策略，为培养学生的高阶思维提供了经验借鉴。

单元教学理念是单元教学设计的核心，主张改变过于注重以课时为单位的教学设计，推进单元整体教学设计，体现数学知识之间的内在逻辑关系以及学习内容与核心素养表现的关联。根据课程标准，教学目标的设定要依据核心素养的内涵和不同学段的主要表现，围绕主题和单元整体设计教学目标，进行具体课时的教学。由此可见，课程标准重视单元整体教学设计在课堂教学中的作用，认为确定单元目标，并将其落实到各个教学环节，可以促进学生对教学内容中概念和原理的理解，提高学生的数学学科核心素养，发展学生的高阶思维能力。这与将单元教学设计与课时教学设计结合起来，体现数学学科的整体性，发展学生的“四基”“四能”，落实数学学科核心素养的观点相契合。［6］单元教学设计是以单元整体为基础形成的教学模式，主张学习的内容应该是整合的、系统的，而不是分割的、独立的。它以教材为基础，对书本中具有联系的知识进行分析与重组，经过整合形成系统的教学单元，脱离以课时为单位的传统教学设计的桎梏。［7］单元教学能够优化教学设计，对提升学生高阶思维能力具有重要的意义。

近年来，ADDIE模型受到众多学者的关注，钟启泉认为单元教学可以选用ADDIE模型来设计，ADDIE模型从分析（Analysis）、设计（Design）、开发（Development）、实施（Implement）、评价（Evaluation）五个步骤，系统、全面地刻画了教学设计。［8］杨倩颖将ADDIE模型运用在初中物理单元教学中，讨论了将ADDIE模型应用于初中物理单元教学的有效性［9］；杨美礼基于ADDIE模型，结合分析化学的特点，建立分析化学课程思政模式［10］；祁卉璇在高等教育中应用ADDIE模型，将ADDIE模型与翻转课堂教学相结合，为翻转课堂教学模式的发展提出建设性意见［11］。

本文以人教版数学九年级下册第二十七章“相似”为例，从高阶思维能力培养的角度，借助ADDIE模型探讨“相似”单元教学设计与策略。

二、基于高阶思维能力培养的“相似”单元教学流程和设计

本节基于ADDIE模型，结合课程标准，制订“相似”单元教学设计，包括以下流程：教学内容分析、单元教学设计、单元整体教学设计评价。

（一）“相似”教学内容分析

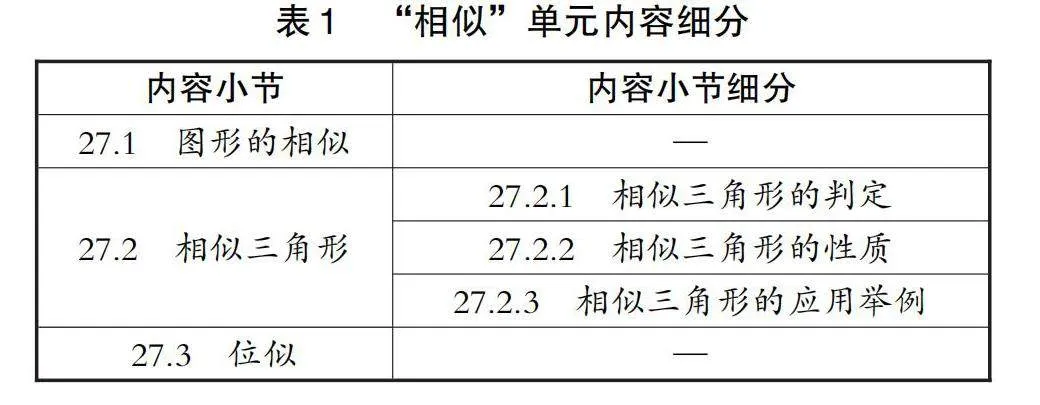
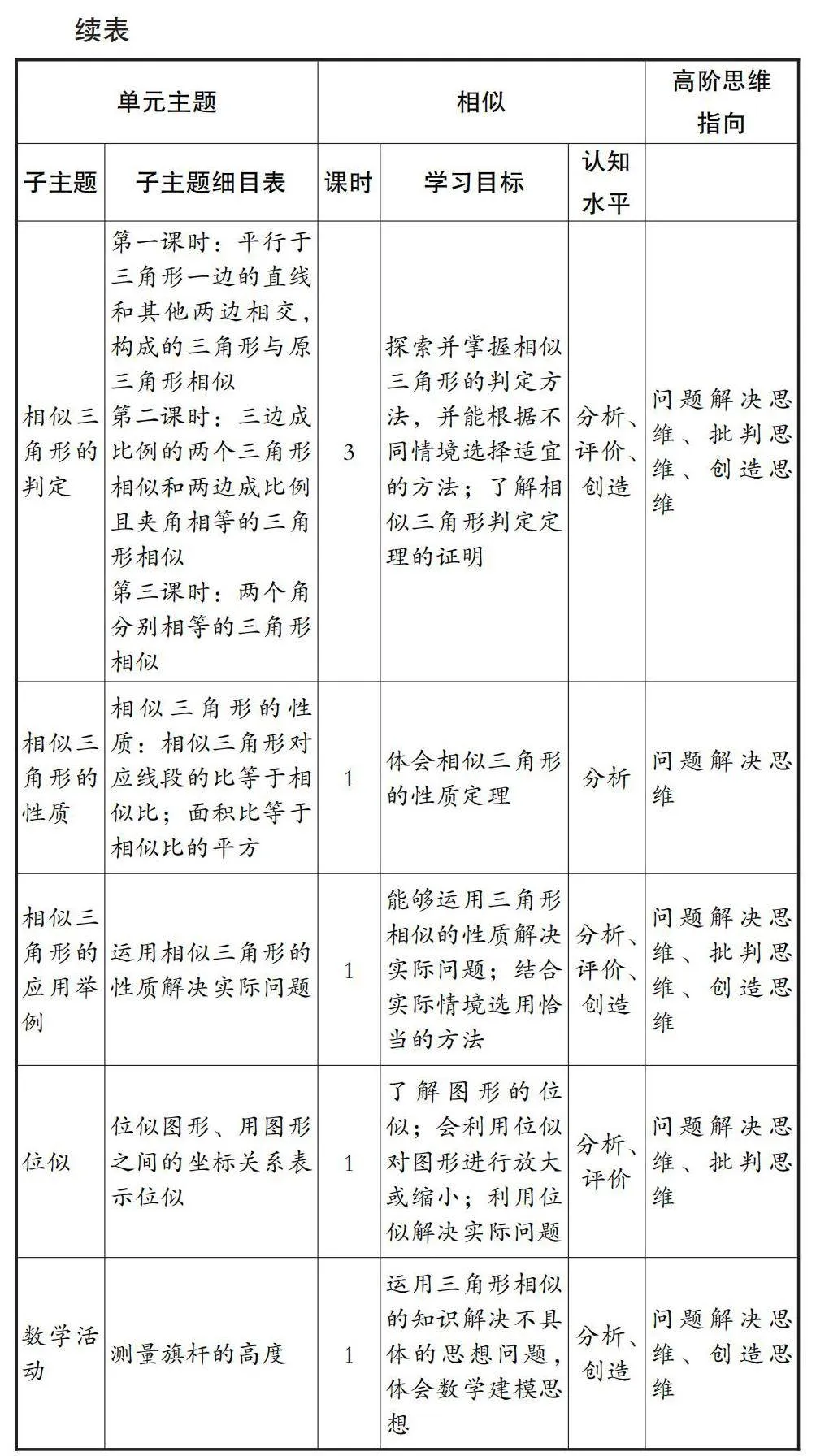
数学教材直接体现数学课程内容和数学学科设计的理念、思想，反映了国家的意识形态和教育理念。［12］对单元知识进行整合不能游离于教材，而是要对教材和课程标准进行全面解读，明确整个初中阶段的数学知识结构分类和大致体系。通过对“相似”单元所在教材进行详细研读，发现“相似”的知识细化为三个小节，具体的知识点分布如表1所示。

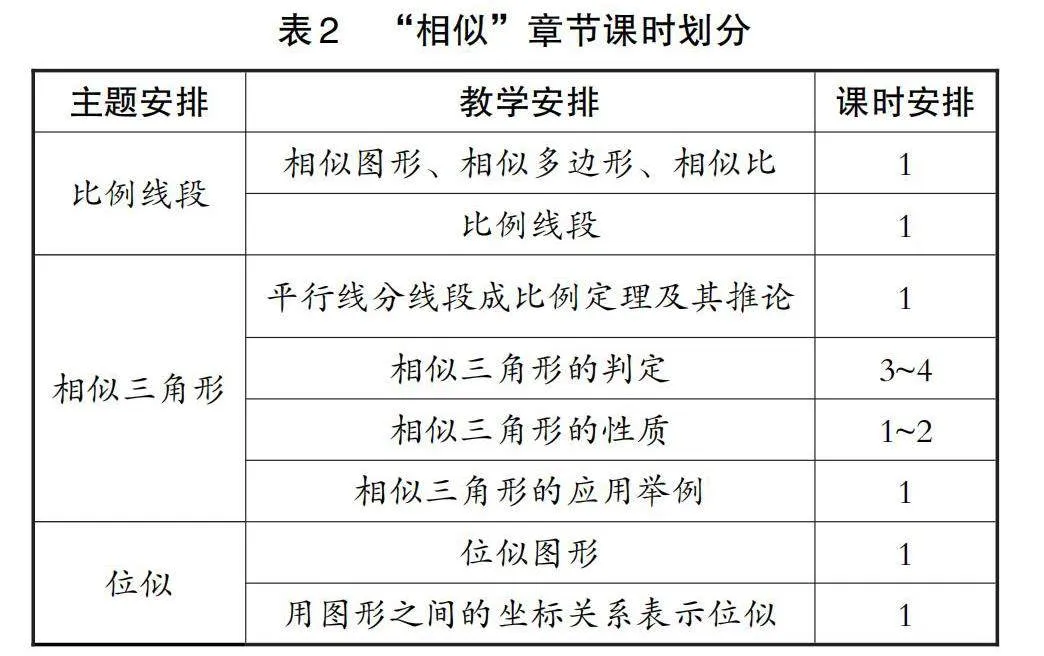
“相似”在课程标准中隶属于“图形与几何”领域的第二个主题“图形的变化”。课程标准强调从运动变化的观点来研究图形，理解图形在轴对称、旋转和平移时的变化规律和变化中的不变量。结合课程标准发现，本单元内容都指向“相似”这个概念。课程标准强调比例的基本性质、线段的比、成比例的线段的重要性，而教材“相似”这一章节并未将其单独设置为一个小节。为促进学生高阶思维能力的提升，同时考虑到知识之间的逻辑与关联，以及学生的整体水平和“最近发展区”，笔者对个别知识内容和顺序进行一定的调整，具体课时划分如表2所示。

（二）“相似”单元教学设计

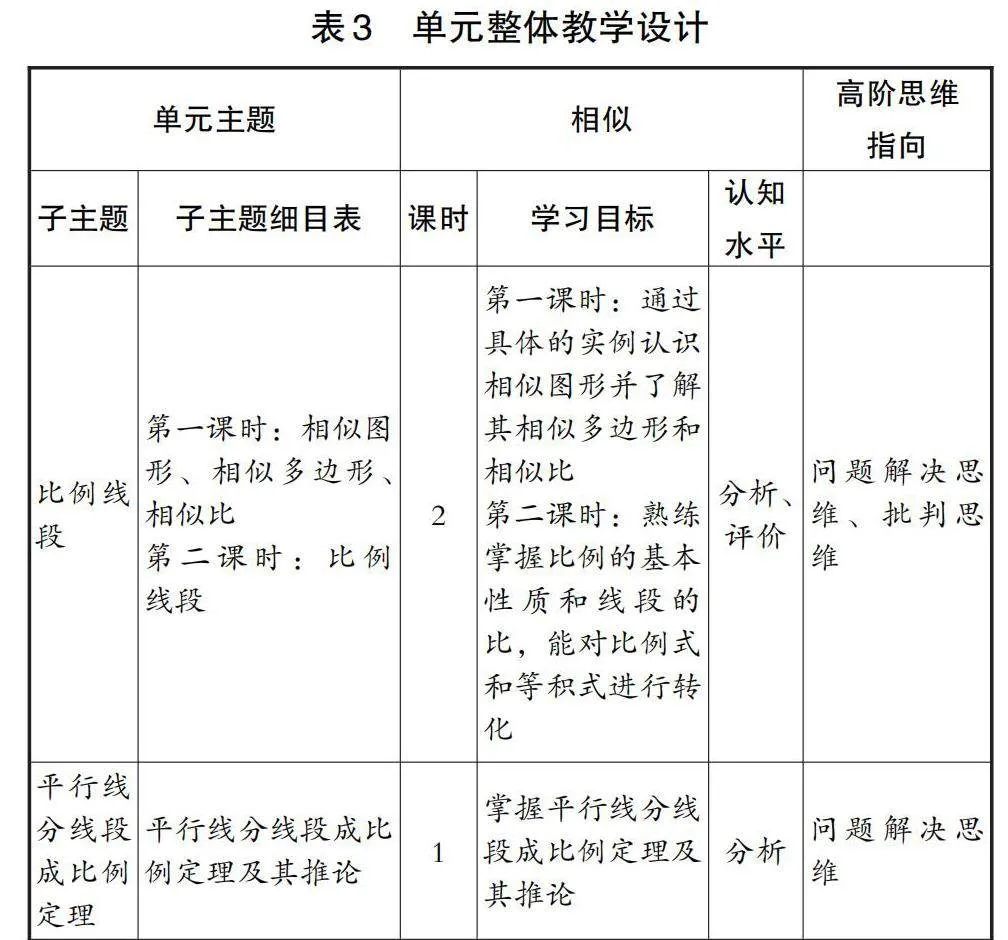
学习目标指学生经历教学活动后表现出来的可见行为的明确表述，其明确了学习内容，有助于达成单元目标，达到课程标准的要求。［13］结合“相似”教学内容分析，本单元整体教学设计主要围绕教学内容和学习目标进行，并根据课程标准和学生个体发展水平确定认知水平，最终指向对应的高阶思维，具体设计如表3所示。

（三）单元整体教学设计评价

教学评价是对教学工作质量所作的分析和评定，是对教学活动整体功能的评价，由此判断教学设计的效果，并加以改进以达到最终目的。数学课堂教学评价是对数学课堂教学活动的价值性判断，对引领、促进数学课堂主体有效活动具有至关重要的作用。［14］对于“相似”这一章节而言，教学评价不能只关注学生对“相似”单元知识的理解与掌握，还要注重学生高阶思维能力的发展程度。对开放性试题进行评价一般用到SOLO分类理论，SOLO分类理论是基于皮亚杰认知发展理论、以等级描述为特征的质性评价方法［15］，根据学生对问题的回答赋予不同的分数，从而量化学生的高阶思维能力，进而实现间接测量的目的。例如根据图1，当满足什么条件时，[△AOB～△COD]，请写出所有可能的情况。

若学生不能给出答案，则判断学生此时的思维水平为低水平，积3分；若学生能够回答出[∠A=∠D]或[∠B=∠C]或[OAOD=OBOC]中的其中一个或两个答案时，则判断学生此时的思维水平为中水平，积6分；若学生能够回答出[∠A=∠D]、[∠][B=∠C]和[OAOD=OBOC]三个完整的答案并给出详细的理由时，则判断学生此时的思维水平为高水平，积10分。根据学生的测验分数综合评价，判断“相似”单元整体教学设计的效果，并加以改进，以促进学生高阶思维能力的发展。

三、基于高阶思维能力培养的单元教学策略

（一）设计单元教学关联，奠定高阶思维发展

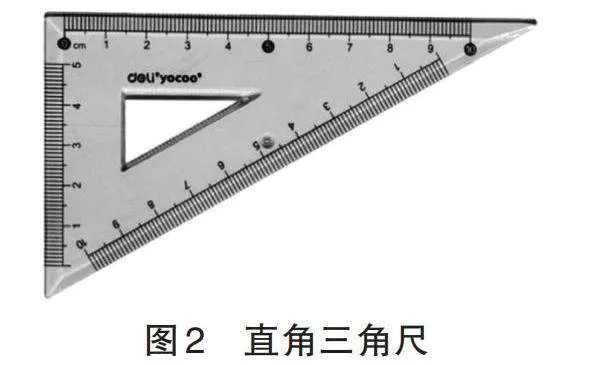
数学情境是指为了完成某个给定的数学教学任务，运用注入式或映射式的方式创设情境并融入数学场域中，从而强化学生的数学意识与数学素养。［16］因此，在单元教学设计中创设适宜的数学情境，可以使学生对学习内容有整体认识，学生在情境中可以快速理解单元主题，激发学习兴趣和求知欲望。例如教学“相似三角形的判定”这一内容时，教师可以利用学生经常使用到的数学工具来创设以下情境：如图2所示，观察直角三角尺，其内外轮廓构成的两个三角形是否相似？你是怎么判定的？在课堂的起始激发学生的学习兴趣，鼓励学生借助所学知识进行思考，引导学生尝试用不同的方法解决问题，发展批判思维能力。

随后教师利用信息技术软件呈现相应的图片并向学生提问：在△ABC和△DEF中，ÐA=ÐD，那么当△ABC和△DEF都是正三角形时，△ABC和△DEF相似吗？当△ABC和△DEF都是等腰三角形时，△ABC和△DEF相似吗？当△ABC和△DEF都是直角三角形时，△ABC和△DEF相似吗？将本单元中几个重要的三角形相似的判定方法结合起来，每个问题都基于“ÐA=ÐD”这一情境问题，使学生在探索的过程中体会本单元知识点的关联性，为高阶思维的发展奠定基础。

（二）关注单元整体构建，促进高阶思维发展

高阶思维能力强调学生对深层次知识的认识，对学生灵活运用知识、综合解决问题提出较高的要求。基于高阶思维能力培养的数学教学不能只关注学生当下学习的知识点，而要从整体上把握各部分知识的关联。因此，教师需要关注单元教学的整体设计，将相似知识点串联起来，建立前后课时的内在逻辑联系。例如先带领学生学习平行线分线段成比例定理及其推论，在学生掌握了两条直线被一组平行线（不少于3条）所截，截得的对应线段的长度成比例后，再讲授相似三角形判定的不同方法，在学习相似后引入位似的概念，让学生深入理解知识间的逻辑关系。在这个过程中，教师需要了解学生的已有认知结构，结合最近发展区，带领学生进行由浅入深的梯度式学习，这有助于学生的思维从低层次的知道、领会、应用，逐步发展到高层次的分析、评价、创造。

（三）着眼单元变式教学，引导高阶思维生成

变式作为数学课堂教学中一种重要的教学方式，它的出现改变了教师授课时以单一讲授式为主的教学方式。张奠宙认为，数学变式就是在不同角度、不同方面、不同背景，从多个维度变更数学对象的含义以及数学问题的呈现形式，使数学内容的本质保持不变的教学方式。［17］变式通过不断更变问题的非本质属性、改变问题的非必要条件，提出蕴含新数学概念、数学原理的新问题，引导学生从多个角度思考问题的概念，从而发现并把握问题的本质。因此，在单元整体教学过程中，教师以问题变式为线索，采用课堂变式训练的方式，从多个视角设问，避免学生陷入思维定式。

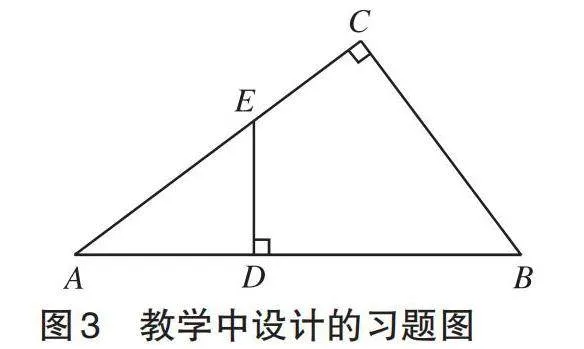
例如在教学过程中，教师设计以下问题：如图3所示，Rt△ABC中，∠C=90°，AB=10，AC=8，E是AC上的一点，AE=5，ED⊥AB，垂足为D，求AD的长。

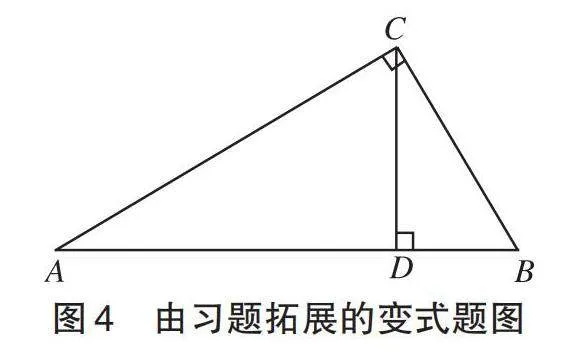
可对上述习题进行变式：如图4所示，在Rt△ABC中，∠C=90°，CD是斜边AB上的高。求证：△ACD [∼]△ABC。

在单元教学过程中，着眼单元整体开展变式教学，对拓展学生的思维有着重要作用。学生在解题过程中，根据变式结构深入思考概念的本质属性，基于问题的不同视角感悟基本思想、积累基本活动经验，直至完全掌握概念，提高问题解决思维能力。

【参考文献】

［1］钟志贤．如何发展学习者高阶思维能力？［J］．远程教育杂志，2005（4）：78.

［2］梁伟虹，熊应龙．以项目式学习促学生高阶思维发展：“宝贝市集”探究项目的设计与实施［J］．基础教育课程，2019（6）：20-23.

［3］胡军，栗小妮，李建华．数学高阶思维培养中的“学生提问”策略［J］．数学通报，2021，60（9）：37-40，封底.

［4］谭师龙．指向高阶思维的小学低段数学综合与实践课的教学设计［D］．重庆：西南大学，2022：摘要Ⅰ-Ⅱ.

［5］方立新，刘新春．促进数学高阶思维实现的问题驱动教学：以“函数单调性”一轮复习为例［J］．数学通报，2023，62（4）：49-52.

［6］章建跃．《普通高中教科书·数学（人教A版）》“单元一课时教学设计”体例与要求［J］．中学数学教学参考，2019（8）：14-16.

［7］吕世虎，吴振英，杨婷，等．单元教学设计及其对促进数学教师专业发展的作用［J］．数学教育学报，2016，25（5）：16-21.

［8］钟启泉．学会单元设计［J］．新教育，2017（14）：1．

［9］杨倩颖．基于ADDIE模型的初中物理单元教学设计与实践研究［D］．重庆：西南大学，2022：摘要Ⅰ.

［10］杨美礼．基于ADDIE模型的分析化学课程思政探索与实践［J］．化学教育（中英文），2023，44（22）：41-51.

［11］祁卉璇．论ADDIE模型对翻转课堂教学设计的启示［J］．中国成人教育，2016（17）：107-109.

［12］张倩，黄毅英．教科书研究之方法论建构［J］．课程·教材·教法，2016，36（8）：41-47.

［13］李玉刚．促进表现性评价的学习目标和表现量规的编制与实施［J］．上海教育科研，2023（5）：61-65.

［14］孙元勋，沈有建，赵京波．数学课堂教学质量评价指标体系（EIMT）的构建与实施［J］．数学通报，2021，60（6）：45-50.

［15］鲁依玲，夏玉梅，宁连华．基于SOLO分类理论的高考数学试题分析：以2022年全国数学新高考Ⅰ卷为例［J］．数学教育学报，2023，32（3）：18-23.

［16］张定强，张元媛，王彤．数学情境教学：理解现状与增润课堂［J］．中小学教师培训，2017（5）：58-61.

［17］张奠宙．关于中国数学教育的特色：与国际上相应概念的对照［J］．人民教育，2010（2）：36-38.