以“问”促“学”

摘 要：随着课程改革的不断推进，传统的教育模式和教学理念已经难以满足现代教育需求，教育教学的改革势在必行.在初中数学教学中，以问题为导向，促使学生进行深层次思考，有利于学生主动探究数学知识，培养学生的逻辑思维能力，提升学生的学习效果，帮助学生建立完整的知识体系，全面提升学生的数学素养.基于此，文章围绕以“问”促“学”教学方法，对初中数学问题导向策略进行探究，以期为初中数学教学提供参考.

关键词：初中数学；数学教学；问题导向策略；应用

中图分类号：G632 文献标识码：A 文章编号：1008-0333（2024）29-0035-03

收稿日期：2024-07-15

作者简介：卢玉琴（1979.10—），女，江苏省苏州人，本科，中小学一级教师，从事初中数学教学研究.

美国著名数学家哈尔莫斯曾说过，问题是数学的心脏.他强调围绕问题展开数学教学，即数学教学需要以问题为中心，以问题驱动教学，让学生在解决问题的过程中理解相应的概念与定理.基于此，在初中数学教学中，教师可通过设计不同的问题引导学生学习，并以问题促进学生学习，提升学生的学习效率，发展学生的核心素养.

1 设计生活化问题，培养模型构建意识

数学是一门与生活实际息息相关的学科，源于生活，根植于生活.数学是解决生活问题的钥匙，也是人们生活、学习必不可少的工具.在初中数学教学中，教师可以将各种生活化的内容引入课堂，引发学生的“生活思考”.由此拉近学生与数学的距离，并让学生在比较熟悉的问题情境中主动探索数学知识，同时激发学生的学习兴趣，使数学教学达到事半功倍的效果.

例如，在学习“等腰三角形”时，为了让学生更好地理解轴对称图形的内涵及等腰三角形的有关性质，教师可引入生活中的“盖房子”问题，以此激发学生的探索热情，有助于学生深入学习新知识.

问题1 如图1所示，某学校打算修建一所这种屋顶的房子作为仓库，已知AB=AC，AD为屋顶的立柱，AD⊥BC，BC=6 m，∠BAC=120°，那∠B等于多少度？DC和BD的长度分别为多少？

教师提出这个问题后，组织学生分组思考和讨论，可得出一系列结论.为了让学生进一步理解等腰三角形的有关知识，教师可结合图形给学生讲解等腰三角形的腰、底边、顶角和底角等概念，然后利用其解决问题.易得∠B=30°，DC=BD=3 m.

在教学过程中，教师提出生活化的数学问题，能够激发学生思考的积极性，继而完成对知识的深层次思考和学习.在问题1中，学生对等腰三角形的学习经历了由具体的“物”到抽象的“形”的过程，建立起了等腰三角形的直观模型，不但提升了教学效果，而且对培养学生的学习兴趣有重要作用.

2 设计并列式问题，深化分类讨论思想

新课程标准强调，在初中数学教学中，教师应引导学生主动思考，并教会学生如何思考，提升学生的数学思维能力.笔者认为，以“问”促“学”的教学方法能使学生置身于问题情境中，在教师的引导下自主筛选信息、分析和解决问题，从而达到训练学生思维和问题解决能力的目的.这种方法将学生置于问题解决者的地位，培养学生思考解决问题的能力，促进学生掌握基础知识与基本技能.在初中数学教学实践中，教师要善于激发学生对知识的兴趣，调动学生的非智力因素，引发学生对知识的深度思考，完成高质量的探究学习.

例如，在学习“圆”时，对于“点与圆的位置关系”“一弦对两弧”“圆心与弦的位置关系”等问题，学生很容易出现错误.为此，在教学过程中，教师可为学生设计相应的“学习陷阱”，以此引发学生更深层次的思考，提高学生对已知条件的辨别和处理能力，从而提高学生分析问题和解决问题的能力.

比如，对于“点与圆的位置关系”，学生经常会忽视一种情况，因此教师设计如下相应的“陷阱”.

陷阱1：点Q是⊙O所在平面内的一个定点，若点Q到圆上一点的最大距离和最小距离分别是16和6，则该圆的直径为多少？

陷阱2：点Q是⊙O所在平面内的一个定点，⊙O半径2，若点Q到圆上点的最小距离1，则点Q到⊙O上点的最大距离是多少？

教师提出问题后，虽然有的学生快速地说出了答案，但却掉进了教师设计的“陷阱”中，忽视了其中的一种情况.在教学过程中，教师不必急于否定学生的答案，而是让学生继续思考，激发学生的挑战意识，将学生的思维引向更深的层次.学生仔细思考以后，最终会发现问题的陷阱所在.

3 设计递进式问题，提升逻辑思维能力

数学知识之间普遍存在着紧密联系.在教学实践中，教师要善于对学生进行引导，帮助学生构建更为完善的知识体系，进而促使学生思维能力、推理能力不断发展.因此，教师可以根据教学内容，设计“问题链条”，以促使学生深度思考，提升学生学习效率，从而实现能力与素养的培养［1］.

例如，在学习“一次函数”时，教师可设计一个“问题链条”，以此还带领学生开展探究性学习.

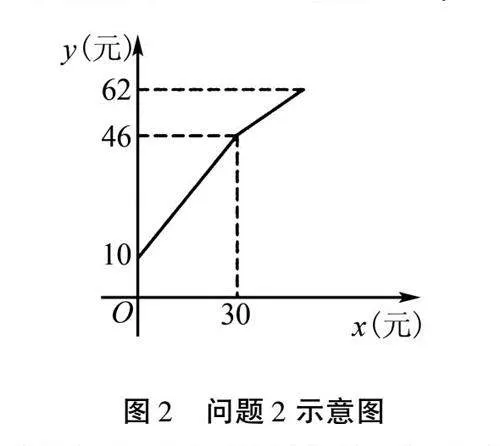
问题2 水果店老板卖西瓜，提前准备了一些零钱备用，他先按照市场价格卖了一些西瓜，然后又降价卖了一些，他手中的钱的数量和西瓜重量的关系如图2所示，请思考如下问题：

（1）水果店老板一共准备了多少零钱？

（2）降价之前，每千克西瓜的售价是多少元？

（3）如果降价之后按照每千克0.8元的价格将西瓜卖完，这时水果店老板手中的钱数一共是62元，请问他一共购进了多少千克西瓜？

设计从易到难、层层递进的“问题链条”，能够帮助学生对问题展开探究性思考，使学生快速掌握问题的核心，为其在短时间内解决问题创造便利条件.递进式问题不但能够调动学生的学习热情，而且能够有效提升课堂教学效率.

4 设计引导式问题，突破难点内容学习

在初中数学教学中，不仅要重视基础知识教学，而且要重视培养数学思想，让学生在思考和学习的过程中逐步把握数学知识的内涵，抓住数学的“灵魂”，进而完成高质量的探究学习.为此，教师可以设计引导式问题.问题的设计应重视内容的选取，遵循学生的认知发展规律.在问题解决过程中，教师应引导学生理解和掌握思考方法，促使学生的数学素养不断发展.

例如，在学习“相似三角形”时，教师可围绕“相似三角形的性质和判定”优化教学，设计相应的问题让学生思考，由此突破教学的重点和难点，并帮助学生掌握思考的方法.

问题3 如图3，点D是△ABC的边BC上的一个点，已知BD∶DC=2∶1，E是AD的中点，连接BE并延长交AC于F，那BE∶EF的值是多少？

为此，教师可提出两个相关的思考性问题：

（1）欲求两条线段的比值，一般需证明三角形相似.在此题中，哪对三角形是你要选择的证明对象？

（2）图3中有没有与△AEF相似的三角形？如果没有与其相似的三角形，该如何解决本题？

此问题能够为学生提供思考方法.学生按照这种方法思考，能够成功锁定△AEF为证明的目标之一.随后继续进行深层次思考，不能找出与△AEF相似的三角形，从而可选择其他方式构造三角形，使其与△AEF相似，继而完成问题的解答.

在整个思考和解决问题的过程中，教师通过引导式问题，为学生提供思考的方法，并且在逐步深入探索的过程中，能够完成对有关重点和难点知识的理解，使学生掌握数学学习的方法.

5 设计差异化问题，助力课后内化迁移

数学教学模式的优化涵盖各个教学环节，其中包含课后巩固思考.课后练习有助于学生巩固所学知识，并让学生在迁移运用中内化所学知识，提升数学能力［2］.因此，教师可在课后通过“问题引入”促进学生的深度学习，帮助学生“当堂学习，当堂消化”，

掌握基础知识，实现高质量学习.

例如，在学习“一元二次方程”后，教师可根据班级学生的实际情况，将其划分成“A”“B”“C”三个层次，并设计相应的问题.问题的设置需兼顾普适性与深入性原则，既要保证全体学生积极参与，又要具有一定的讨论、探究价值.

“A”层次针对基础薄弱的学生，主要问题有：

（1）方程x2-75x+350=0，3x2-6x=20是一元二次方程吗？

（2）自编两个一元二次方程.

对于这个层次的学生，需强化其数学学习自信心和学习兴趣，设计这样的问题能够达到此目的.

“B”层次针对中等水平学生，提出的问题有：

（1）方程x2-x=44，1x2-9x-90=0是不是一元二次方程？它们有什么共同点和不同点？

（2）在x-2x2+5=0，4x2-5y-1=0，ax2+bx+c=0，（m-1）2=1中，哪些是一元二次方程？

对于这个层次的学生，需要培养其克服困难的信心和决心，这样的问题设计可以强化学生对基本概念的理解，并获得成就感，使其在今后学习遇到困难时能自己解决问题.

“C”层次针对能力较好的学生，

可设计这样一道问题：

如果方程（m+1）x|4m|-2+27mx+5=0是关于x一元二次方程，那么m的值为多少？

对于这个层次的学生，需激励他们突破自我，向更好的方向发展.设计这样的问题，能够使学生综合已学知识，构建更为完善的知识体系.

6 结束语

在初中数学教学中，合理运用问题导向策略，可以更好地激发学生探究学习的热情，让学生在思考的过程中深化对知识的理解，不断提升数学核心素养.为此，教师可以围绕“以问促学”的理念优化教学模式，引导学生学习与探索，锻炼其思维能力，让学生从“问题”中获得知识与能力，进而完成对学生核心素养的培养.

参考文献：［1］ 何强.问题导学法在小学数学教学中的运用实践［J］.基础教育论坛，2022（35）：87-88.

［2］ 任亚男.问题导学法在初中数学课堂中的运用策略［J］.当代家庭教育， 2022（29）：125-128.

［责任编辑：李 璟］