平面几何中的动点问题研究


摘 要:动点问题是初中平面几何中的常见问题,也是历年中考的热点问题,倍受命题者青睐.这类问题涉及的知识点多,形式丰富多样,求解方法灵活,对学生而言具有一定的难度.基于此,文章介绍与矩形、菱形有关的动点问题,以及与动点有关的三角形的存在性问题,并给出这几类动点问题的解题思路.,以期为初中数学教学提供参考.
关键词:平面几何;动点问题;最值问题;存在性问题
中图分类号:G632 文献标识码:A 文章编号:1008-0333(2024)29-0026-03
收稿日期:2024-07-15
作者简介:林庄园(1991.1—),女,广西桂林人,本科,中学一级教师,从事初中数学教学研究.
与动点有关的最值问题和存在性问题是平面几何中的难点.根据图形结构特征,抓住动点在运动过程中的不变量以及动点的运动轨迹,再合理利用几何性质,是解决这类问题的基本思路.
1 点在矩形的一边上运动
例1 如图1所示,矩形ABCD中,AB=6,BC=10,点E在边AD上,且AE=2,F为边AB上的一个动点,连接EF,过点E作EG⊥EF交直线BC于点G,连接FG,若P是FG的中点,则DP的最小值为( ).
A.9105 B.6 C.5 D.210
解析 因为四边形ABCD是矩形,所以∠BAD=∠ABC=∠BCD=∠ADC=90°,且DC=AB=6,AD=BC=10.
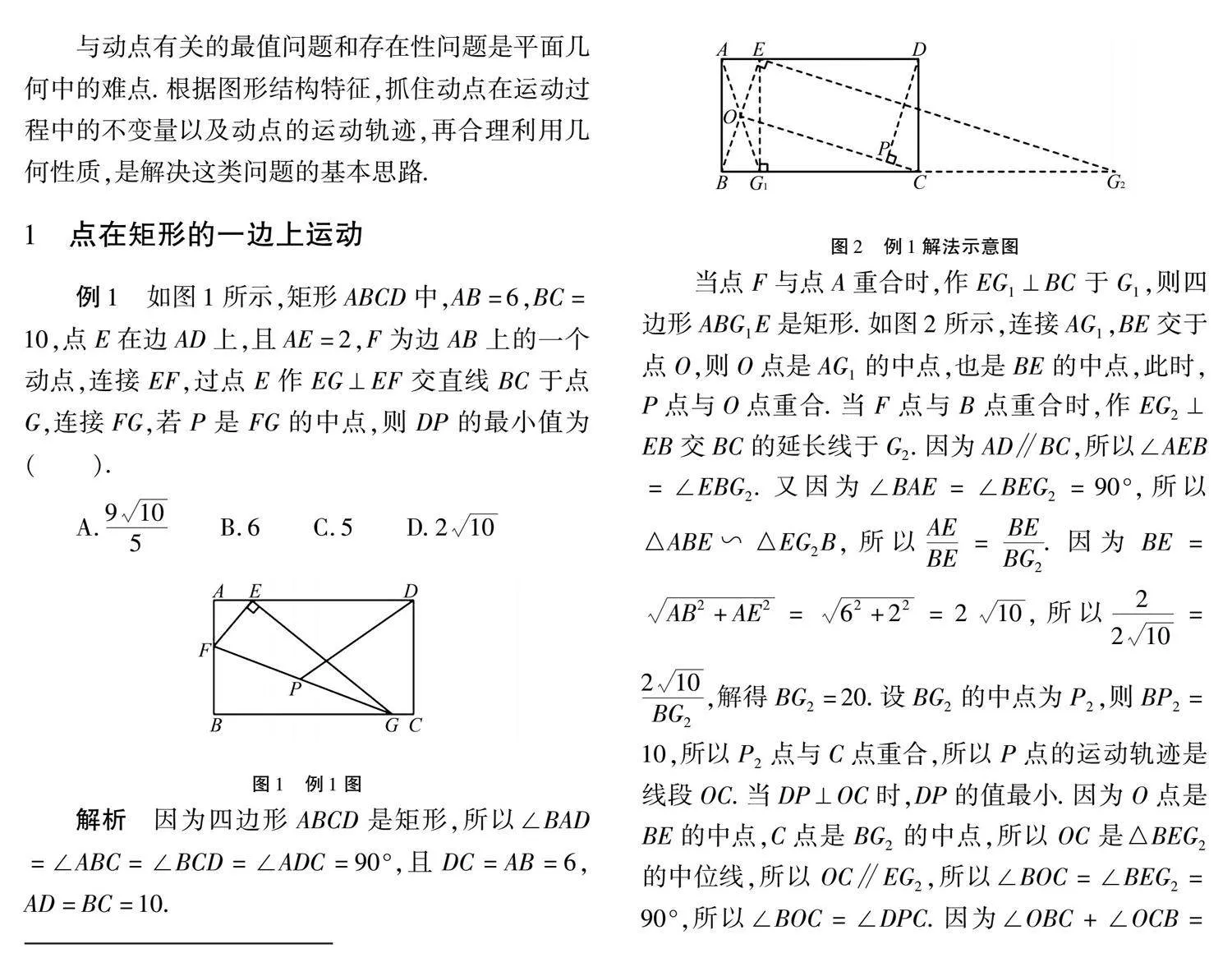
当点F与点A重合时,作EG1⊥BC于G1,则四边形ABG1E是矩形.如图2所示,连接AG1,BE交于点O,则O点是AG1的中点,也是BE的中点,此时,P点与O点重合.当F点与B点重合时,作EG2⊥EB交BC的延长线于G2.因为AD∥BC,所以∠AEB=∠EBG2.又因为∠BAE=∠BEG2=90°,所以△ABE∽△EG2B,所以AEBE=BEBG2.因为BE=AB2+AE2=62+22=210,所以2210=210BG2,解得BG2=20.设BG2的中点为P2,则BP2=10,所以P2点与C点重合,所以P点的运动轨迹是线段OC.当DP⊥OC时,DP的值最小.因为O点是BE的中点,C点是BG2的中点,所以OC是△BEG2的中位线,所以OC∥EG2,所以∠BOC=∠BEG2=90°,所以∠BOC=∠DPC.因为∠OBC+∠OCB=90°,∠OCB+∠PCD=90°,所以∠OBC=∠PCD,所以△OBC∽△PCD,所以OCDP=BCDC.因为BO=12BE=10,BC=10,所以OC=BC2-BO2=310,所以310DP=106,解得DP=9105.故选A.
点评 本题是一道矩形中的动点问题,难度较大,综合性较强.解题的关键是要找出P点的运动轨迹.作EG1⊥BC于G1,连接AG1,BE交于点O,作EG2⊥EB交BC的延长线于G2.当F点与A点重合时,G点与G1点重合,此时P点与O点重合.当F点与B点重合时,G点与G2点重合,此时P点与C点重合,因此P点的运动轨迹就是线段OC.当DP⊥OC时,DP的值最小.根据△OBC∽△PCD,列比例式求出DP的长即可.
2 菱形上的动点
例2 如图3,在边长为4的菱形ABCD中,∠A=60°,点M是AD边的中点,点N是菱形内一动点,且MN=1,连接CN,则CN的最小值为_______.
解析 过点M作MH⊥CD交CD的延长线于点H,如图4所示.因为四边形ABCD是菱形,∠A=60°,所以AB∥CD,所以∠HDM=∠A=60°,所以∠HMD=30°.因为点M是AD边的中点,所以DM=12AD=2,所以DH=12DM=1.根据勾股定理得HM=DM2-DH2=3.因为CD=4,所以CH=CD+DH=4+1=5.根据勾股定理,得CM=HM2+CH2=27.因为MN=1,当点N运动到线段CM上的点N′时,CN取得最小值,CN′=CM-MN=27-1,即CN的最小值为27-1.
点评 本题主要考查菱形的性质、直角三角形的性质、勾股定理、线段最短等知识,解题的关键是求出CM的长.过点M作MH⊥CD交CD的延长线于点H,根据菱形的性质以及直角三角形的性质求出CM=27-1,当点N运动到线段CM上的点N′时,CN取得最小值,进一步求解即可.
3 点在曲线上运动
例3 如图5所示,A是函数y=2x的图象上的点,B2,2,C-2,-2,试利用性质:“函数y=2x的图象上任意一点A都满足AB-AC=4”求解下面问题:作∠BAC的内角平分线AE,过C作AE的垂线交AE于点F,已知当点A在函数y=2x的图象上运动时,点F总在一个圆上运动,则这圆的半径为( ).
A.12 B.1 C.2 D.4
解析 如图6所示,作BD⊥AE,垂足为M,交AC于点D.
因为AE平分∠BAC,BD⊥AE,所以∠DAM=∠BAM,∠AMD=∠AMB=90°.因为AM=AM,所以△ABM≌△ADM,所以AD=AB,所以CD=AC-AD=AC-AB=4,即CD的长为定值4.过点M作MN∥CD交CF于点N,因为BD⊥AE,CF⊥AE,所以DM∥CF,所以四边形CDMN为平行四边形,所以MN=CD=4.因为∠MFN=90°,所以点F在以线段MN为直径的圆上,因为MN=4,所以点F运动所在圆的半径为2.选C.
点评 本题是一道新定义问题,主要考查全等三角形的判定与性质、平行四边形的判定与性质、圆周角定理等知识.根据新定义添加辅助线,构造全等三角形和平行四边形是解题关键.
4 存在性问题
例4 如图7所示,等边△ABC的顶点A,B,C均在坐标轴上,其中B(-4,0),C(4,0).
(1)如图7,若将△AOC沿AC翻折得到△ACD,则A点坐标为_______,D点坐标为_______;
(2)在(1)问的条件下,点E为y轴正半轴上一动点,是否存在点E使得BDE为等腰三角形?如果存在,请直接写出BDE的面积,若不存在,请说明理由.
解析 (1)如图7中,过点D作DH⊥x轴于H.
因为B(-4,0),C(4,0),所以OB=OC=4.因为△ABC是等边三角形,所以AB=AC=BC=8,∠ACO=60°.因为∠AOC=90°,所以OA=AC2-OC2=82-42=43,所以A0,43.
因为将△AOC沿AC翻折得到△ACD,所以∠ACD=∠ACO=60°,CD=CO=4,所以∠DCH=180°-60°-60°=60°,因为DH⊥CH,所以∠DHC=90°,所以∠CDH=30°,所以CH=12CD=2,所以DH=CD2-CH2=42-22=23,OH=OC+CH=6,所以D6,23.
(2)存在.如图8,设BD交y轴于F,E(0,m).
由题意得∠BAC=60°,∠CAD=∠CAO=30°,所以∠BAD=90°.因为AB=8,AD=43,所以S△ABD=12·AB·AD=12·AF·xD-xB,所以AF=8×4310=1635,所以OF=43-1635=435.
①当EB=ED时,42+m2=62+m-232,解得m=833,所以E0,833,所以S△EBD=12×833-435×10=2833.
②当BD=BE′时,m2+42=102+232,解得m=46或-46(舍弃),所以E′0,46,所以S△BDE=12×46-435×10=206-43.
③当DB=DE″时,62+m-232=102+232,解得m=219+23或-219+23(舍弃),所以E0,219+23,所以S△BDE=12×219+23-435×10=1019+63.
综上所述,△BDE的面积为2833或206-43,或1019+63.
点评 本题主要考查坐标与图形的性质、两点间的距离公式、勾股定理、三角形的面积公式、等边三角形的性质及翻折对称变换等知识,难度较大,需注意分类讨论和方程思想在解题过程中的应用.
5 结束语
与动点有关的最值问题或者存在性问题,是初中数学教学的难点.教师可利用信息技术手段给学生展开动点的运动过程及运动路径,从“形”与“数”融合的角度去教学,让动态问题直观化,这样便于学生理解问题的本质[1] .
参考文献:[1] 杨金宝,邹靓靓.初中平面几何中的“以静制动”[J].理科考试研究,2013(8):6-7.
[责任编辑:李 璟]

