分类讨论思想在解决几何问题中的应用

摘 要：几何探索性问题是历年中考的热点，经常以中考压轴题的形式出现.这类问题综合性强，涉及的知识点多，解法灵活多样，承载着一定的选拔功能，对学生而言具有一定的难度.在解决这类问题的过程中，通常需综合运用多种数学思想与方法.基于此，以一道中考试题为例，重点分析分类讨论思想在解决几何压轴题中的应用，以期为初中数学教学提供参考.

关键词：分类讨论思想；几何问题；压轴题；应用

中图分类号：G632 文献标识码：A 文章编号：1008-0333（2024）29-0008-03

收稿日期：2024-07-15

作者简介：仇春学（1979.1—），男，陕西省大荔县人，本科，中学一级教师，从事初中数学教学研究.

中考压轴题一般为几何探索题，具有开放性和综合性的特点，考查的知识点较为全面，涉及多种数学思想与方法，对学生而言具有一定的难度. 笔者以2023年深圳市中考数学第22题为例，探讨分类讨论思想在解决几何问题中的应用，供读者参考.

1 试题呈现

（2023年深圳市中考数学第22题）（1）如图1，在矩形ABCD中，E为AD边上一点，连接BE.①若BE=BC，过C作CF⊥BE交BE于点F，求证：△ABE≌△FCB；②若S 矩形ABCD=20时，则BE·CF=_______．

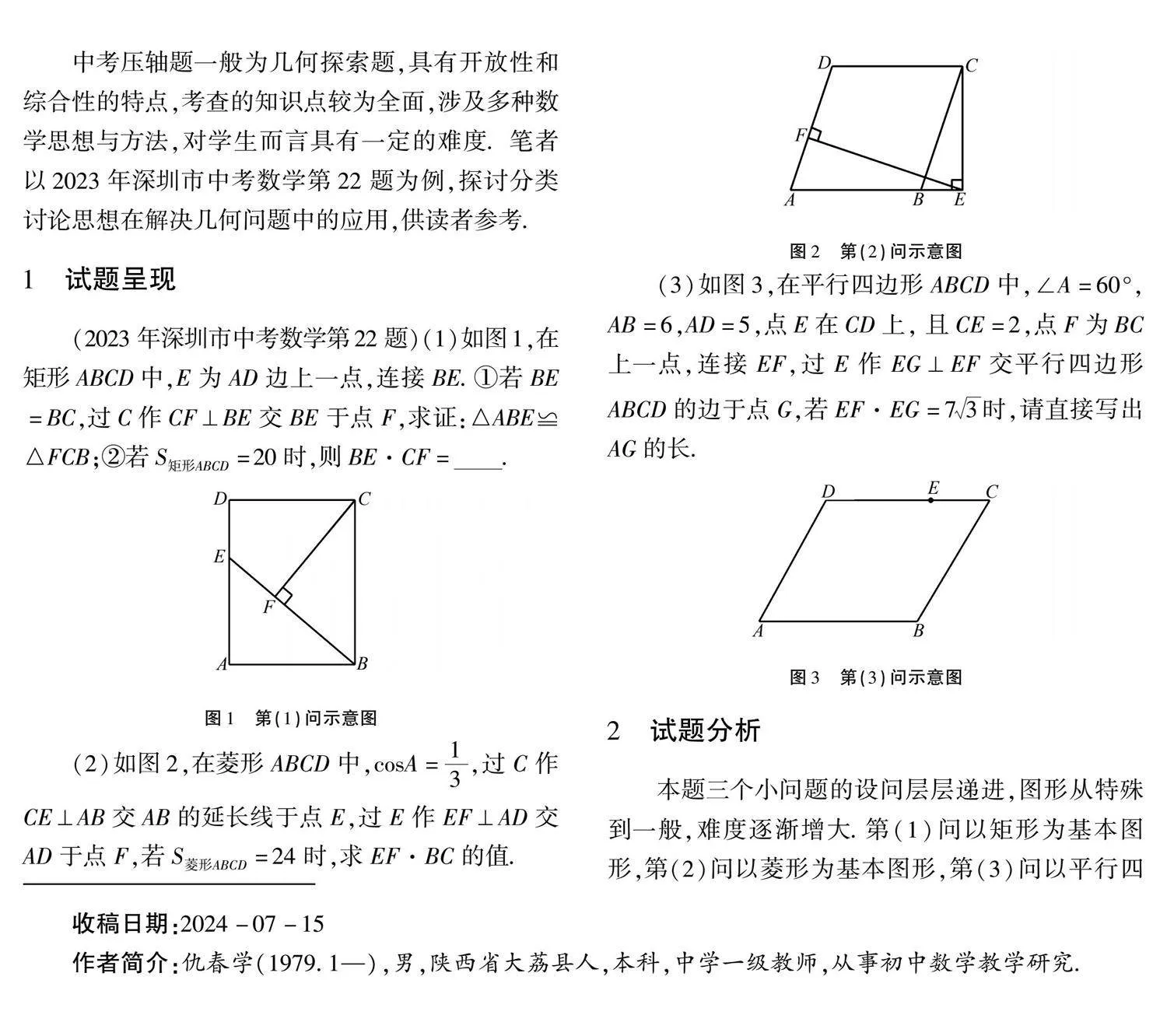
（2）如图2，在菱形ABCD中，cosA=13，过C作CE⊥AB交AB的延长线于点E，过E作EF⊥AD交AD于点F，若S 菱形ABCD=24时，求EF·BC的值.

（3）如图3，在平行四边形ABCD中，∠A=60°，AB=6，AD=5，点E在CD上， 且CE=2，点F为BC上一点，连接EF，过E作EG⊥EF交平行四边形ABCD的边于点G，若EF·EG=73时，请直接写出AG的长.

2 试题分析

本题三个小问题的设问层层递进，图形从特殊到一般，难度逐渐增大.第（1）问以矩形为基本图形，第（2）问以菱形为基本图形，第（3）问以平行四边形为基本图形［1］.从知识点上看，本题主要考查矩形的性质、全等三角形的性质与判定、菱形的性质、解直角三角形、相似三角形的性质与判定、平行四边形的性质等知识.从思想方法上看，本题考查分类讨论思想、转化与化归思想、模型思想、方程思想等数学思想方法.因此，本题的综合性较强，对学生分析问题和解决问题的能力有较高的要求，是一道具有一定区分度的中考压轴题.

3 解法赏析

第（1）问较简单，根据矩形的性质可得∠ABE+∠CBF=90°，又由CF⊥BE可知∠FCB+∠CBF=90°，从而可证明∠FCB=∠ABE.结合已知条件BE=BC，可证明△ABE≌△FCB，从而AB=CF，因此BE·CF=BC·AB=S 矩形ABCD=20.

评析 第（1）问主要考查矩形的性质、矩形的面积公式、全等三角形的判定与性质，属于基础题.

第（2）问也比较容易，根据菱形的性质可得AD//BC，所以∠CBE=∠EAF.又因为EF⊥AD，CE⊥AB，所以∠AFE=∠BEC=90°，所以△AFE∽△BEC，所以AEBC=EFCE=AFBE，所以EF·BC=AE·CE.又因为cosA=13且∠CBE=∠A，所以BE=BC·cos∠CBE=BC×cosA=13BC，所以AE=AB+BE=AB+13BC=AB+13AB=43AB，即EF·BC=AE·CE=43AB×CE=43S菱形ABCD=43×24=32.

评析 第（2）问主要考查菱形的性质、相似三角形的判定与性质、锐角三角函数的概念、线段关系的转化等知识，属于中低档题.

第（3）问是本题的难点，下面进行详细分析.

分析 此问的难点在于点G的位置不确定.一些学生缺乏分类讨论思想，误以为点G只能在AD边上，从而造成漏解.事实上，点G可能在AD边上、AB边上或BC边上，因此，要分三种情况讨论，要求学生具备分类讨论思想［2］.

①当点G在AD边上时，如图4，延长FE，交AD的延长线于点M，连接GF，过点E作EH⊥DM于点H.

因为四边形ABCD是平行四边形，AB=6，CE=2，所以CD=AB=6，DE=DC-EC=6-2=4.因为DM//FC，所以△EDM∽△ECF，所以EMEF=EDEC=2.考虑△MGE和△FEG，它们以GE为公共高，所以S△MGES△FEG=EMEF=2，所以S△MGE=2SΔEFG=EF·EG=73.在Rt△DEH中，∠HDE=∠A=60°，则EH=32DE=32×4=23，DH=12DE=2，所以12MG×HE=3MG=73，所以MG=7.又GE⊥EF，EH⊥MG，所以∠MEH=90°-∠HEG=∠HGE，所以△MEH∽△EGH，所以HEHG=HMHE，即HE2=HM·HG.设AG=a，则GD=AD-AG=5-a，GH=GD+HD=5-a+2=7-a，HM=GM-GH=7-（7-a）=a，所以（23）2=a（7-a），解得a=3或a=4，从而可知AG=3或AG=4.

评析 对于点G在AD边上的情况，其解题过程分为以下几步：一是先将FE延长与AD的延长线相交于点M，由“X型”相似模型可证△EDM∽△ECF，从而由相似三角形的性质可得EM=2EF；二是根据已知条件EF·EG=73可得到2S△EFG=73，再根据△MGE和△FEG共高可得S△MGE=2S△EFG=73；三是考虑△MGE的底边MG，这条边上的高可以根据含30°角的直角三角形的性质求出，从而利用等面积法即可求出MG；四是根据关系HE2=HM·HG求出AG.事实上，关系式HE2=HM·HG即为射影定理，但由于射影定理不是初中数学教材中的结论，所以在以上解答中，给出了关系式HE2=HM·HG的证明过程.

②当点G在AB边上时，如图5，连接GF，延长GE交BC的延长线于点M，过点G作GN∥AD，则GN∥BC，四边形ADNG是平行四边形.

设AG=x，易知DN=AG=x，EN=DE-DN=4-x.因为GN∥CM，所以△ENG∽△ECM，所以EGEM=GNCM=ENEC=4-x2，所以CM=2GN4-x=104-x.考虑△GEF和△MEF，它们以EF为公共高，所以SΔGEFS△MEF=EGEM=ENEC=4-x2，又因为2S△GEF=EF·EG=73，所以S△MEF=2S△GEF4-x=734-x.过点E作EH⊥BC于点H，在Rt△EHC中，EC=2，∠ECH=60°，所以EH=3，CH=1，所以S△MEF=12×MF×EH，则12×3×MF=734-x，所以MF=144-x，所以MH=CM+CH=104-x+1=14-x4-x，FH=MF-MH=144-x-14-x4-x=x4-x.因为∠MEF=∠EHM=90°，所以∠FEH=90°-∠MEH=∠EMH，所以△FEH∽△EMH，所以FHEH=EHMH，所以EH2=FH·MH，即（3）2=x4-x×14-x4-x，解得x1=32，x2=8（舍去），即AG=32.

评析 对于点G在AB边上的情况，其解题过程与情形①类似，分为以下几步：一是设AG=x，将GE延长与BC的延长线相交于点M，构造“X型”相似模型，证明△ENG∽△ECM，再由相似三角形边的比例关系求出CM的表达式；二是根据△GEF和△MEF共高和条件EF·EG=73可得S△MEF的表达式；三是利用等面积法可得MF的表达式；四是根据关系EH2=FH·MH列出方程，从而求出AG.

③当G点在BC边上时，如图6，过点B作BT⊥DC于点T，则S△BTC＞S△EFG.

在Rt△BTC中，CT=12BC=52，BT=3TC=532，S△BTC=12BT×TC=12×532×52=2538.因为EF·EG=73，所以S△EFG=723.因为2583＜723，即S△BTC＜S△EFG，矛盾.故G点不可能在BC边上.

综上所述，AG的长为 3或4或32.

4 结束语

在初中阶段，分类讨论思想已经得到了广泛应用，但学生的分类讨论思想较为薄弱，因此，在中考试题中合理渗透分类讨论思想有利于选拔具备较高数学素养的学生.在平时教学中，教师要向学生渗透分类讨论思想，引导学生利用分类讨论思想解决问题，提高学生运用所学知识分析问题和解决问题的能力，提升学生的数学核心素养.

参考文献：［1］ 徐茜敏.分类讨论：建构初中数学严谨的思维方式［J］.数理天地（初中版），2023（11）：56-58.

［2］ 沈俊杰.分类讨论思想在初中数学解题中的应用［J］. 中学数学（下半月），2023（8）：52-53.

［责任编辑：李 璟］