空间惯性传感器地面隔振摆台建模与分析

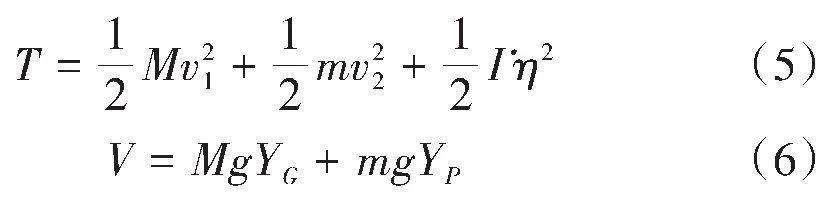
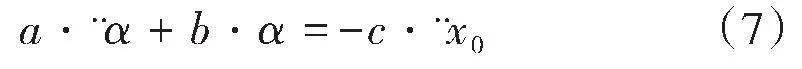
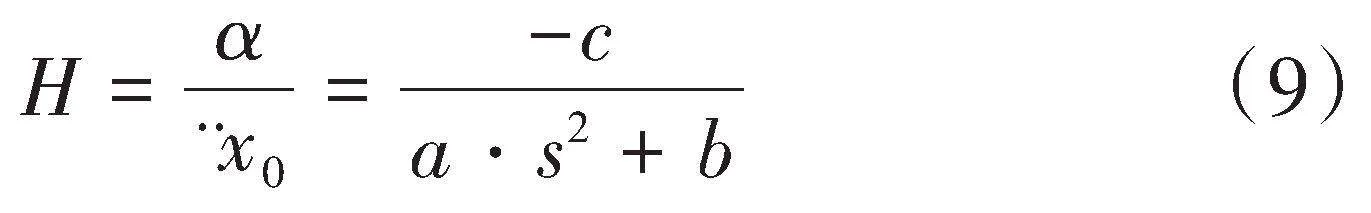
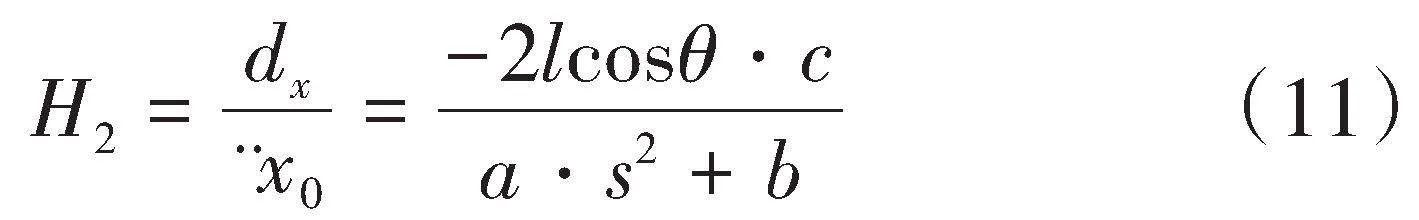
摘 要：空间惯性传感器是空间引力波探测任务的核心技术之一，在地面对其性能研究时不可避免地受到地面振动的影响。文章聚焦于惯性传感器悬丝悬挂地面研究方案中隔振系统的基础理论与关键技术，提出一种地面振动隔离方案并进行了建模分析。首先介绍了基于罗伯茨连杆机构的低频水平隔振方法，并对其进行了详细的理论建模；其次，分析了不同关键参数下，隔振摆台的隔振效果，确定了影响摆台隔振性能的主要因素，为下一步空间惯性传感器地面隔振系统的搭建和优化提供了一定的理论依据。

关键词：空间惯性传感器；罗伯茨连杆；地面振动噪声；振动抑制

中图分类号：TB535" "文献标识码：A" " 文章编号：[1007] - [9734] （[2024）] [04] - [0]040 - 05

[0] 引 言

基于电容位移传感和静电反馈控制技术的空间惯性传感器具有精度高，体积小，能实现六个自由度同时测量等特点，广泛应用于各种空间计划。从20世纪九十年代以来，空间惯性传感器在卫星重力测量、牛顿反平方定律检验以及引力波探测等空间项目中作为重要载荷得到成功应用，其技术发展不断成熟，俨然成为空间科学任务的重要载荷之一[1-3]。

空间惯性传感器具有较高的分辨率，而动态范围非常小，在地面1g的重力加速度作用下，无法正常工作，因此要设法使它在地面上也能工作，以便研究各因素对其带来的影响，同时对它的各项性能指标进行验证[4-6]。目前主要的地面研究方案包括悬丝悬挂、自由落体和高压悬浮[7，8]。其中，悬丝悬挂方案是一种重要的空间惯性传感器地面研究方案，其原理是用一根极细悬丝悬挂检验质量，用悬丝的张力平衡检验质量受到的重力，由于悬丝扭转刚度极低，因此，检验质量可以绕悬丝扭转方向自由运动，模拟惯性传感器在轨工作时检验质量的自由运动状态，进而对惯性传感器性能进行测试与研究[9-11]。但是，由于受限于地面振动噪声的影响，惯性传感器噪声地面测试水平很难达到空间实验的噪声指标要求[12]。

本文针对空间惯性传感器悬丝悬挂方案地面研究方案中存在的地面振动问题，开展隔振相关研究工作，运用罗伯茨连杆机构构建低频水平隔振模型，将其应用到惯性传感器地面隔振研究工作中，并对其进行详细的建模分析。

[1] 罗伯茨连杆机构

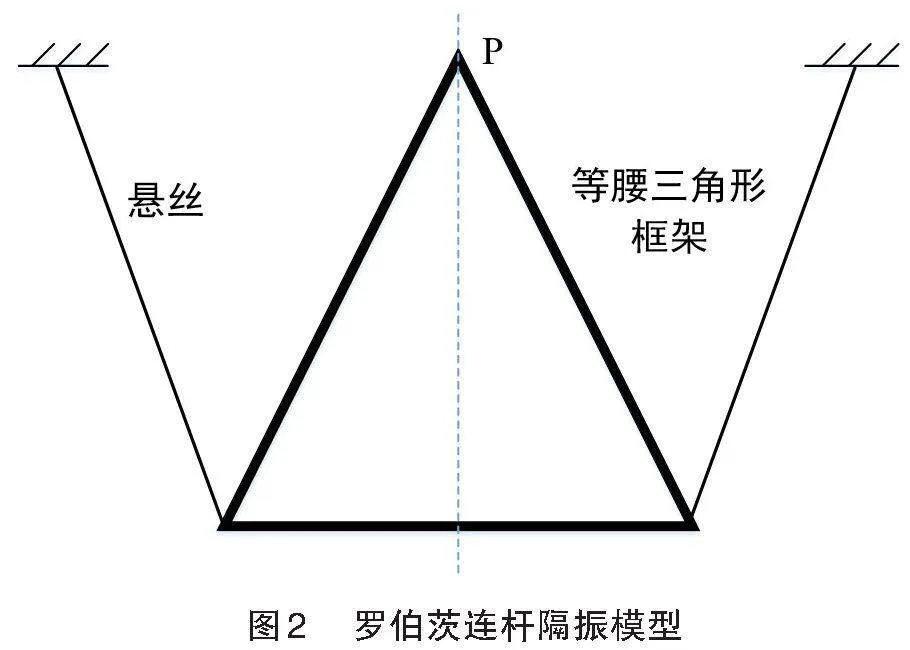
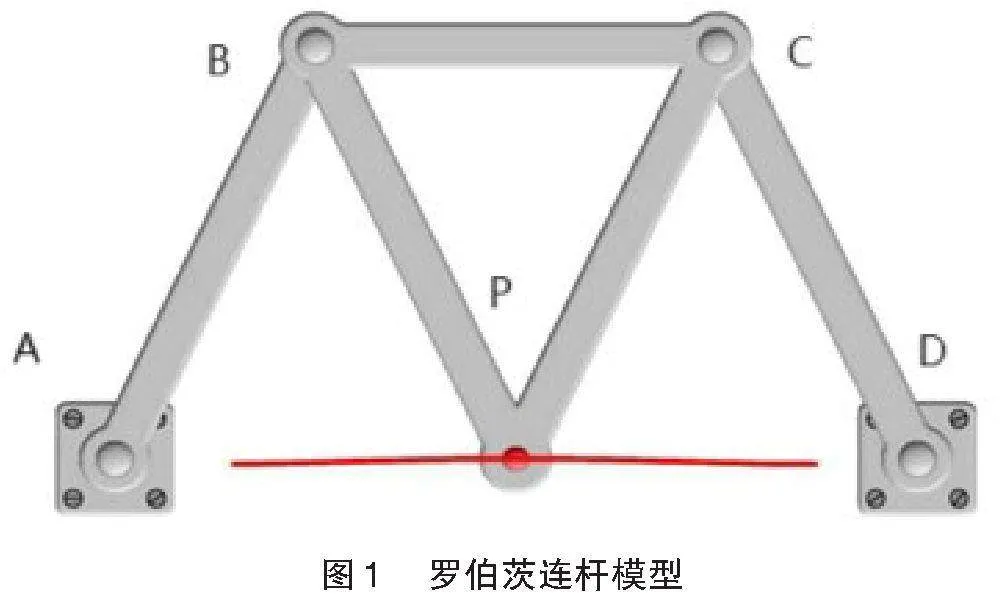
罗伯茨连杆机构是一种对称的连杆机构，与其他近似直线机制不同，该机构在联结器中点处有了延伸。此延伸垂直于连接两个相邻关节的线。联结器延伸的端点在固定枢轴之间的运动生成一条近似直线。罗伯茨还提出了另一种近似解决方案，该解决方案基于连杆机构和等腰三角形。在这种情况下，连杆等长，AB=BP=PC=CD，且下面两个联结点之间的水平距离是上面两个联结点之间水平距离的两倍，即AD=2BC。顶点 [P]的轨迹在小范围内接近一条直线。罗伯茨连杆模型图如图[1]所示。

利用罗伯茨连杆可以使P点产生大致直线运动这一特点，想要构建一个它的倒置的立体模型，即 P点在上。由于罗伯茨连杆是一个特殊的对称结构，为了简化分析过程，可以分析P点在二维平面内的运动，观察它的运动轨迹。如图[2]所示，连杆机构的主体是一个等腰三角形框架，两端由悬丝悬挂。当整个机构左右摆动时，P点会经过一个较为平坦的轨迹，即大致在一个水平面上运动，没有发生倾斜，因而没有竖直方向的上下运动。而势能关于位移的二阶导是刚度系数，当等腰三角形框架的运动轨迹比较平坦时，回复刚度就会比较小，这样就不会引入重力所引起的回复刚度，会使等腰三角形框架运动周期增长。这样以等腰三角形框架为主体构成的罗伯茨连杆机构就形成了一个长周期的隔振摆台。

[2] 隔振摆台的建模与分析

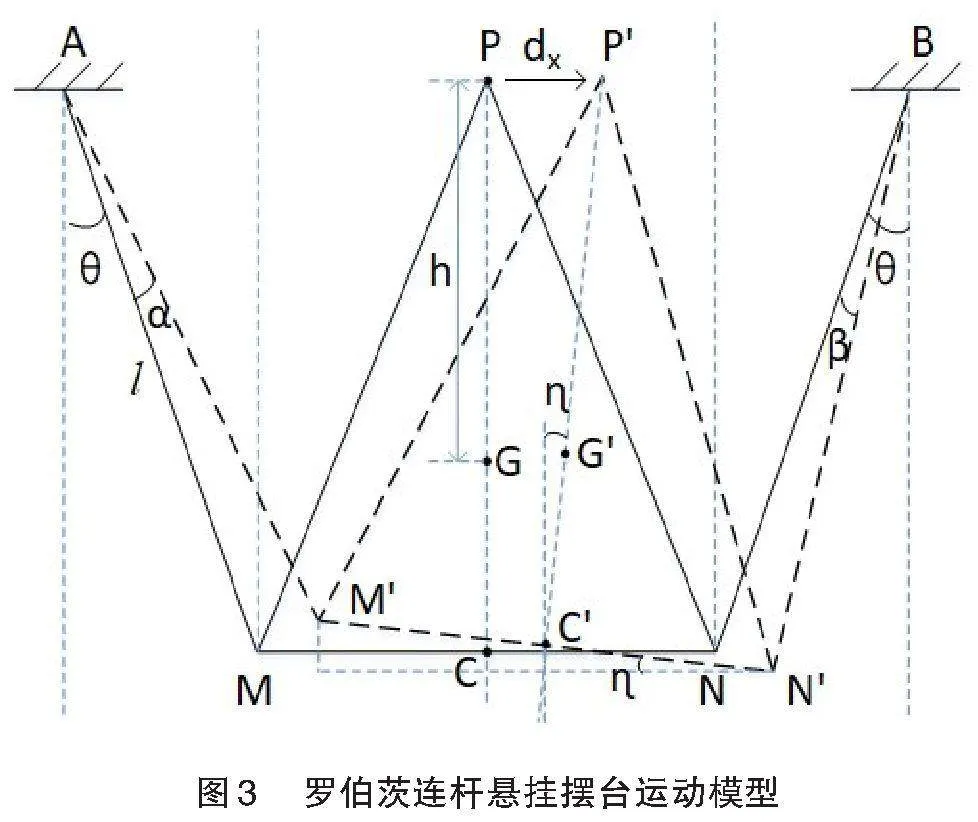
以罗伯茨连杆的一个水平方向为例对其进行建模分析，如图[3]所示。图3中实线所画的结构即为罗伯茨连杆静止时的状态，虚线所画的结构为罗伯茨连杆对外界振动响应后的状态。图中三角形框架PMN是一个等腰三角形结构，且AM=PM=PN=BN，AP=MN=PB。三角形框架两端[MN]由悬丝分别悬挂于A点和B点。假设三角形结构顶点P点为静电加速度计安装位置。为了评估该结构对外界振动的衰减能力，需要计算外界振动到P点位移的传递函数。以AB所在的直线为[x]轴，AB的中垂线为[y]轴，建立直角坐标系。点C是M点和N点的中点，令A点坐标为（[x0]，[y0]），G点为三角形框架的重心，令等腰三角形框架质量为M，P点质量为m。

通过图3中的几何关系，可以求出P点和G点的坐标为：

对连杆系统进行运动学分析，得到系统动能和势能分别为：

其中，[v1]和[v2]为等腰三角形框架和P点的运动速度，I和[η]为等腰三角形框架的转动惯量和转动角度，[YG]和[YP]分别为G点和P点的纵坐标矢量，h为P点到G点的距离，η为P点转动的角度。

忽略系统阻尼和其他外界扰动力的影响，则系统拉格朗日方程如下：

其中：

[a=M2lcosθ-h2+4ml2cos2θ+I]

[b=Mg2ltanθsinθ+h+2mgltanθsinθ] （8）

[c=M2lcosθ-h+mlcosθ]

由此可得外界振动到连杆偏移角[α]的传递函数为：

由图3可知P点位移为：

[dx=2lαcosθ-α2sinθ≈2lαcosθ]" （10）

因此，外界振动到P点位移的传递函数，即摆台的隔振传递函数可以表示为：

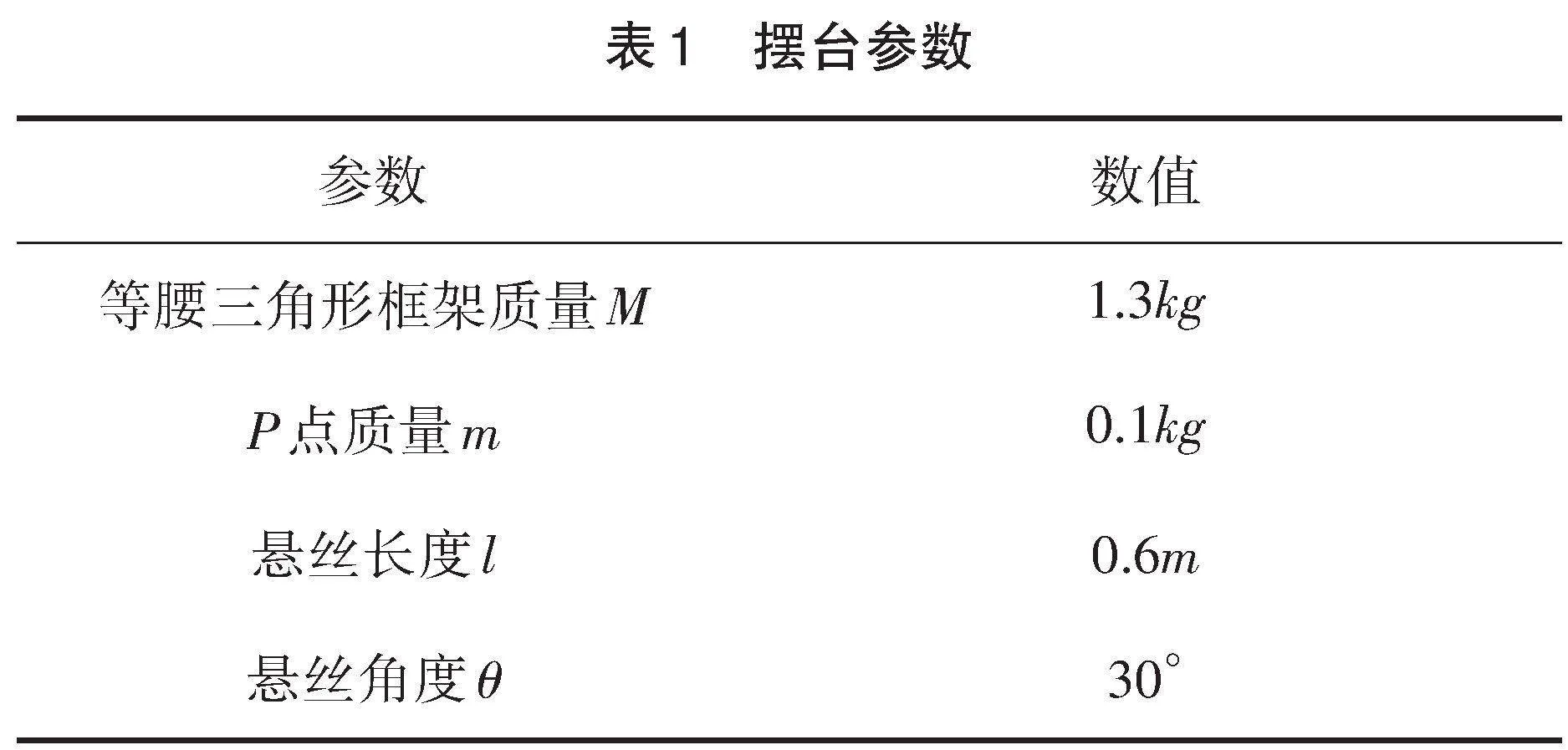
选取一套典型摆台参数，如表[1]所示。

根据表[1]参数画出摆台系统的隔振传递函数曲线如图[4]所示。由图4曲线可以看出，摆台的共振频率在[0.4Hz]处，在共振频率以上的高频段，摆台隔振表现类似于单摆，随着频率的升高，摆台的隔振效果越好。在共振频率以下的低频段，摆台有着接近[20dB]的振动衰减效果。

[3] 结果与讨论

从摆台隔振传递函数表达式（11）中可以看出，摆台的隔振性能主要与摆台系统的质心分布、悬丝的初始角度以及悬丝长度等参数有关。考虑罗伯茨连杆机构的特性，悬丝角度的变化会影响连杆结构以及悬挂摆台的稳定性。因此，考虑到实际应用，各个关键参数之间需要综合考虑其影响。

[3.1]" 悬丝角度

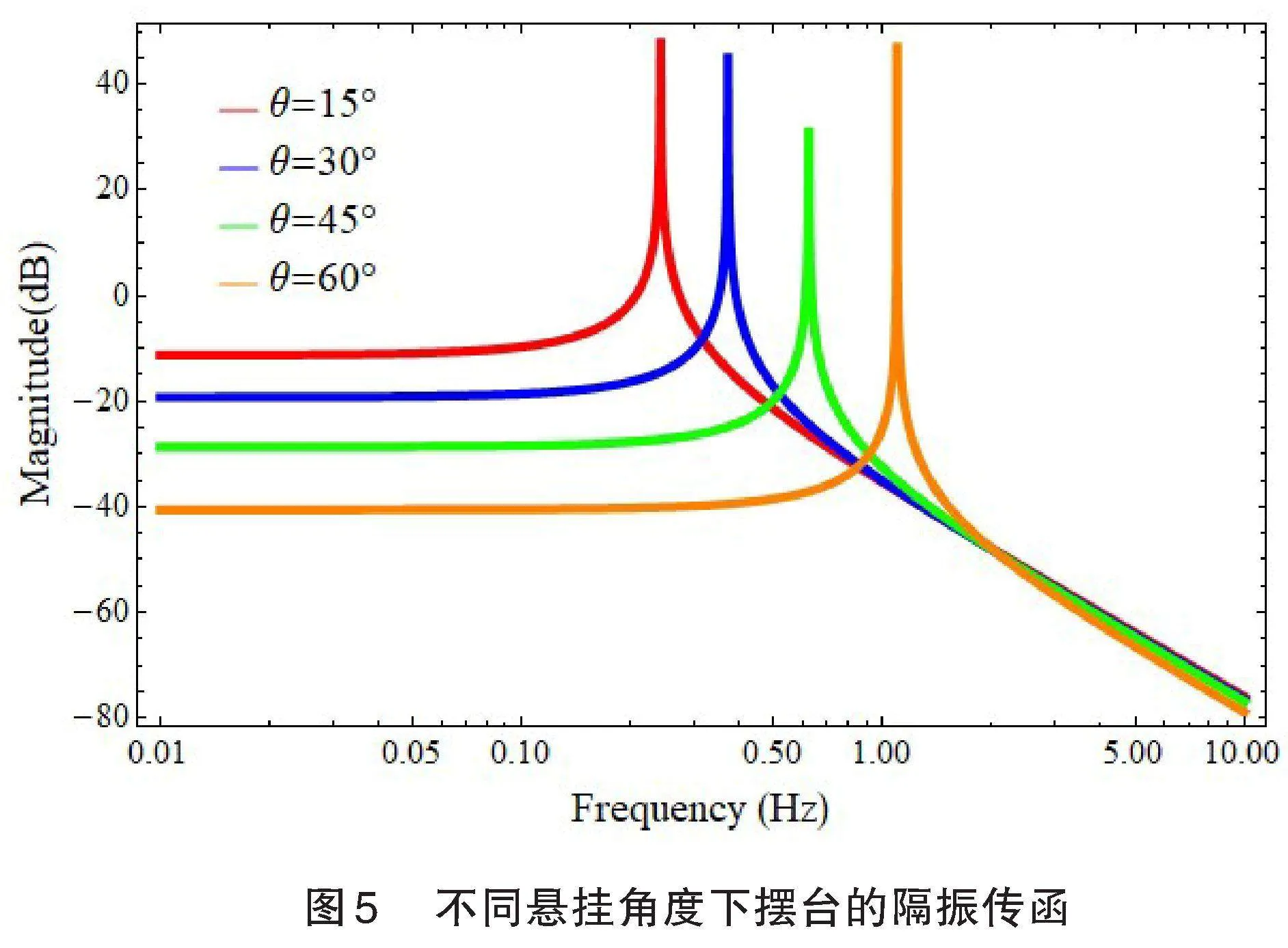
为分析摆台悬丝的角度的影响，绘出悬丝角度θ取不同值时摆台隔振传递函数如图5所示。从图5对比曲线中可以看出，摆台悬丝的角度越大，摆台在低频段的隔振效果越好，当悬丝的角度达到60度时，摆台在低频段的隔振效果接近40dB，隔振效果提升明显。当继续增大悬丝角度时，摆台低频隔振效果进一步提升，但是考虑到摆台结构的稳定性，以及增大悬丝角度所带来的摆台占地面积的增加和纵向空间的压缩，会对实验场所以及待测传感器带来一定的限制，因此，要综合考虑多个因素，选取合适的悬丝角度。

[3.2 ]" 安装位置

实际测试中，待测惯性传感器会安装在悬挂点P正下方，为了分析不同安装位置摆台的隔振效果，计算等腰三角形框架的中垂线PC线段上不同位置点的隔振传递函数的变化。取PC线段上任一点[P1]作为惯性传感器的安装位置，令[h1]为[P1]距离P的长度，则点[P1]的位移为：

[d′x=α2l cosθ-h1+α2h1tanθ≈α2l cosθ-h1] （[8）]

计算摆台PC线段上任一点[P1]的隔振传递函数，选取同样的摆台参数，取PC线段上不同位置点，并画出它们的隔振曲线，如图[6]所示。

图6中的曲线分别代表距离P点0.1m、0.2m、0.3m、0.4m四个位置处的隔振曲线，其中，绿色曲线代表的距离p点0.3m位置处的隔振曲线在低频段的隔振效果最好，接近[40dB]，隔振率没有明显损失，通过质心估算可知该位置距离系统的撞击中心最近。由此可见，悬丝悬挂系统的安装位置以靠近系统撞击中心为原则，以获得最佳的隔振效果。

[4] 结 论

本文针对空间惯性传感器地面研究受限于地面振动噪声的问题，提出了一种基于罗伯茨连杆机构的地面隔振方法，构建了空间惯性传感器地面测试摆台模型，进行了详细的建模分析，得到了其隔振传感，并对摆台结构重要参数进行了重点分析，得到了摆台不同悬挂角度以及不同位置处的摆台隔振率。计算结果表明，选取合适的摆台悬挂角度和待测仪器安装位置，将会获得优于40dB的低频隔振效果，对于加速度分辨率为10-15m/s2/Hz1/2量级的惯性传感器地面研究具有一定的促进作用。同时，也为下一步空间惯性传感器地面隔振摆台的设计搭建和实验研究提供了一定的理论依据。

参考文献：

[[1]]白彦峥，田蔚，周泽兵，等.高精度空间加速度计及其应用[J].空间科学学报，2010，30（6）：601-606.

[[2]]郑伟，许厚泽，钟敏，等.国际下一代卫星重力测量计划研究进展[J].大地测量与地球动力学，2012，32（3）：152-159.

[[3]]吴树范，王楠，龚德仁.引力波探测科学任务关键技术[J].深空探测学报，[2020]，[7（2）]：118-127.

[4]BAI Y， LI Z， HU M， et al. Research and development of electrostatic accelerometers for space science missions at HUST[J]. Sensors， 2017， 17（9）： 1943.

[5]薛大同.静电悬浮加速度计的地面测试与评定方法综述[J].宇航学报，2011，32（8）：1655-1662.

[6]HU S， PEI S， HU M， et al. Noise investigation of an electrostatic accelerometer by a high-voltage levitation method combined with a translation–tilt compensation pendulum bench[J]. Review of Scientific Instruments， 2021， 92（6）.

[7]裴世勋，胡爽，文振华.高压悬浮静电加速度计地面测试隔振系统研究[J].郑州航空工业管理学院学报，2022，40（4）：83-87，94.

[8]谭定银，白彦峥，屈少波，等.空间静电加速度计研究与应用[J].华中科技大学学报（自然科学版），2022，50（9）：96-103.

[9]STANGA R， MARCONI L， GRIMANI C， et al. Double Degree of Freedom pendulum facility for the study of weak forces[J/OL].Journal of Physics： Conference Series. IOP Publishing， 2009， 154（1）： 012032.

[10]TAN D Y， YIN H， ZHOU Z B. Seismic noise suppression for ground-based investigation of an inertial sensor by suspending the electrode cage[J/OL]. Chinese Physics Letters， 2015， 32（9）： 090401.

[11]TU H B， BAI Y Z， ZHOU Z B， et al. Performance measurements of an inertial sensor with a two-stage controlled torsion pendulum[J/OL]. Classical and Quantum Gravity， 2010， 27（20）： 205016.

[12]ZHOU Z B， LIU L， TU H B， et al. Seismic noise limit for ground-based performance measurements of an inertial sensor using a torsion balance[J/OL]. Classical and Quantum Gravity， 2010， 27（17）： 175012.

Modeling and Analysis of Vibration Isolation Pendulum for

Space Inertial Sensors Performance Investigation

Abstract： Space inertial sensors is one of the key technologies in space gravitational wave detection mission， and the performance research of it is inevitably affected by the seismic noise on the ground. This article focuses on the basic theory and key technologies of the vibration isolation system in the ground research scheme of the fiber suspension method of inertial sensors， proposing a ground vibration isolation scheme and conducting modeling analysis. This article introduced a low-frequency horizontal vibration isolation method based on Roberts linkage firstly， and conduct a detailed theoretical modeling. Secondly， analyzed the comparison of the vibration isolation performance of the pendulum under different key parameters， identified the main factors affecting the vibration isolation performance of the pendulum， and provided a theoretical basis for the construction and optimization of the seismic isolation system of the space inertial sensor in the next step.

Key words： space inertial sensor; Roberts linkage; seismic noise; vibration isolation