关于梯形模糊数排序的新方法

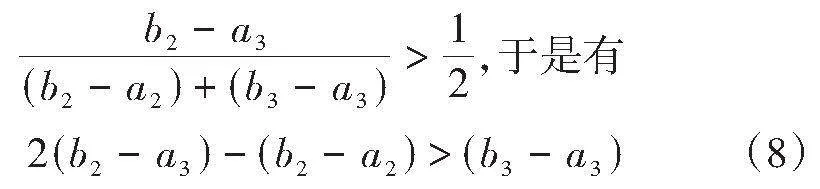
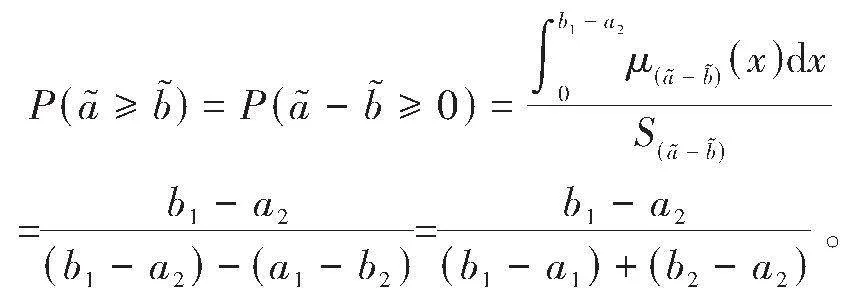
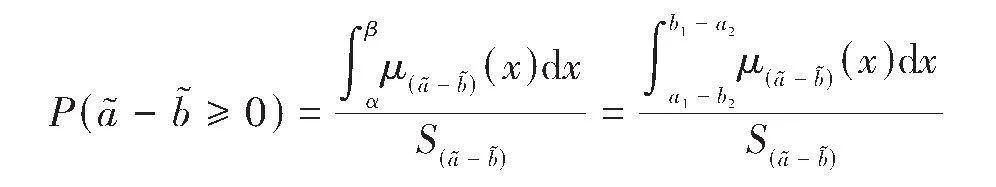
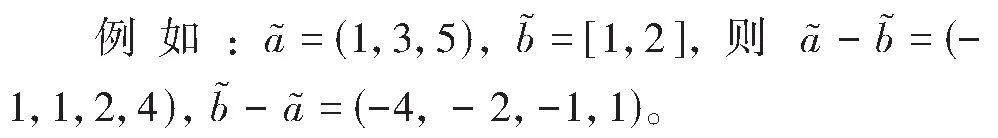
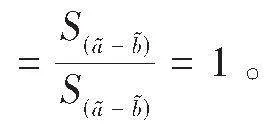
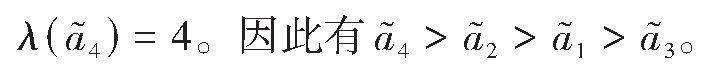
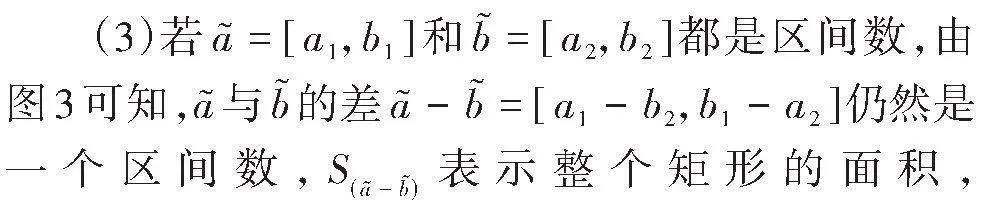
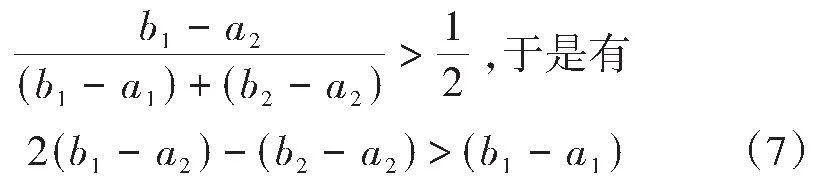
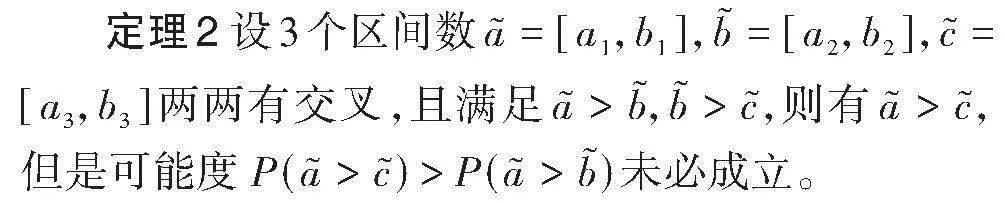
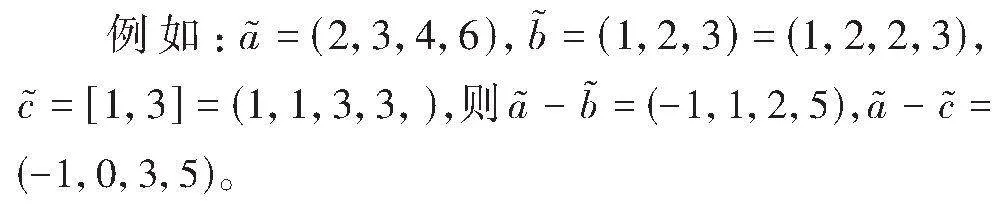
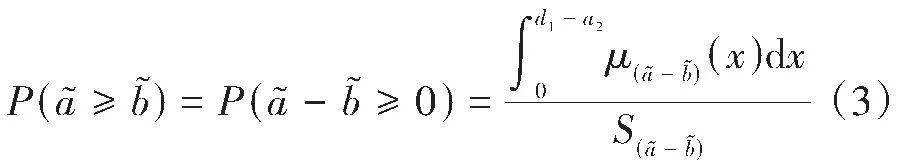
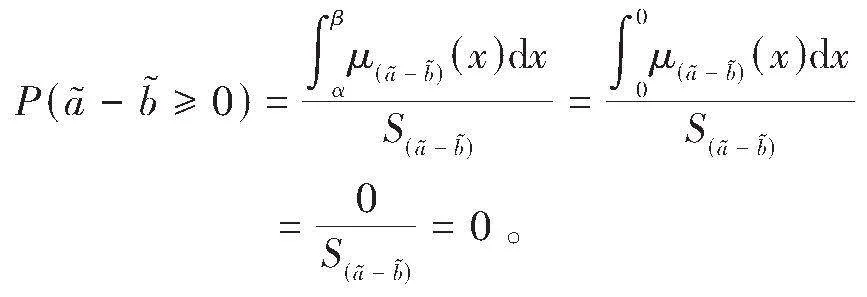
摘 要：关于模糊数排序的问题一直是模糊决策研究的热点。随着研究的深入，研究对象由区间模糊数发展到三角模糊数，进而又发展到梯形模糊数。文章提出一种新的梯形模糊数排序方法，该方法是基于两个梯形模糊数减法法则，通过定积分的运算给出可能度的概念，再利用可能度大小和布尔矩阵法对多个模糊数进行排序。最后通过算例显示该方法的可行性，并通过与近期文献的方法比较，显示其有效性和优效性。研究结果表明，该方法不仅能够比较不同类型的模糊数次序，而且计算简单、区分度强，所以应用范围广泛。

关键词：梯形模糊数；可能度；布尔矩阵；排序

中图分类号：O223；C159 文献标识码：A" 文章编号：1007 - 9734 （2024） 04 - 0106 - 07

0 引 言

模糊决策中关于模糊数排序的问题，一直是研究的热点。常见的模糊数分为区间数、三角模糊数和梯形模糊数三种。关于这些模糊数排序的研究已有大量的成果，其中有关区间模糊数排序方法的成果较多，也较完善[1-4]。在区间数之后发展起来的三角模糊数和梯形模糊数更适合用来表达不确定性问题。三角模糊数和梯形模糊数的排序问题早些年就开始研究了[5-6]，其排序方法的多样性反映在近年来的文献中。Yu等[7]基于质心点的概念提出一种ε偏差度方法；文献[8]提出了一种基于相对优先关系的三角形和梯形模糊数排序方法；Chai等[9]研发了一种模糊数的扩展排序方法，该方法是Dempster–Shafer理论的应用；文献[10]提出了一种应用可能性理论对模糊数进行排序的方法；Hesamian和Bahrami[11]提出了一种基于可信度理论的模糊数排序偏好指数；模糊数的排序方法也可应用在经济数据分析中[12]；文献[13]利用中心平均值法对梯形模糊数进行排序；文献[14]使用参数关系对基于概率的偏好强度指数进行排序。

基于以上概述，可以看出模糊数排序的方法很多，但大多数是同类型模糊数之间比较，对于混合型模糊数不便推广使用。在本研究中，我们将基于两个模糊数的减法运算法则，利用可能度大小进行比较，给出一种新的排序方法。

1 知识回顾

为了表示不确定性，实数被扩展到区间数、三角模糊数以及梯形模糊数。

特别地，当[b=c]时，梯形模糊数[a=（a，b，c，d）]退

两个梯形模糊数满足以下运算法则[15-16]：

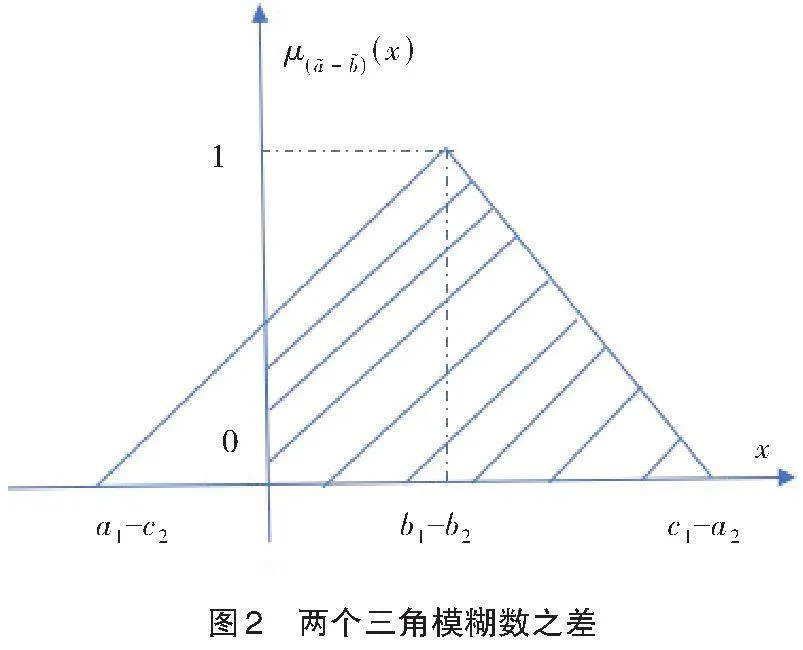
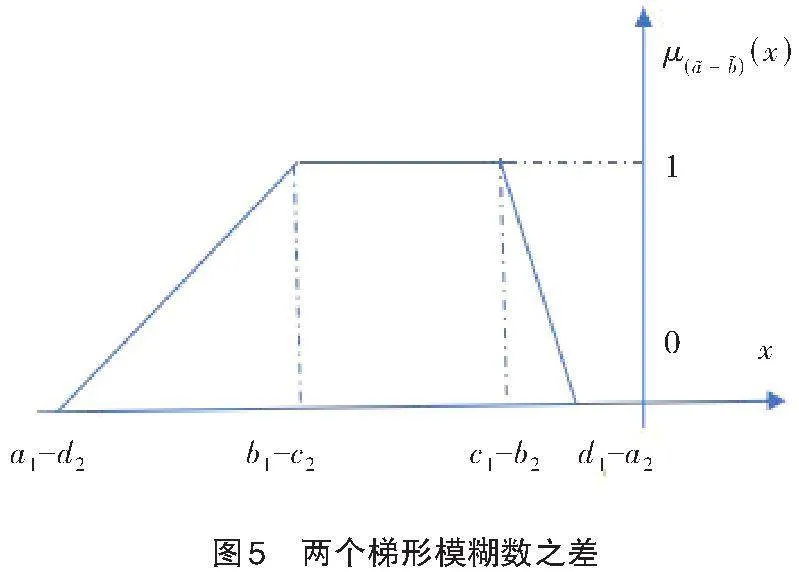
利用两个梯形模糊数的减法运算（或差运算）法则给出下面的定义。

2 两个模糊数大小比较方法

2.1" 基本概念

定义3不仅对两个梯形模糊数适用，还适用于两个三角模糊数、区间数，甚至是不同类型的模糊数。

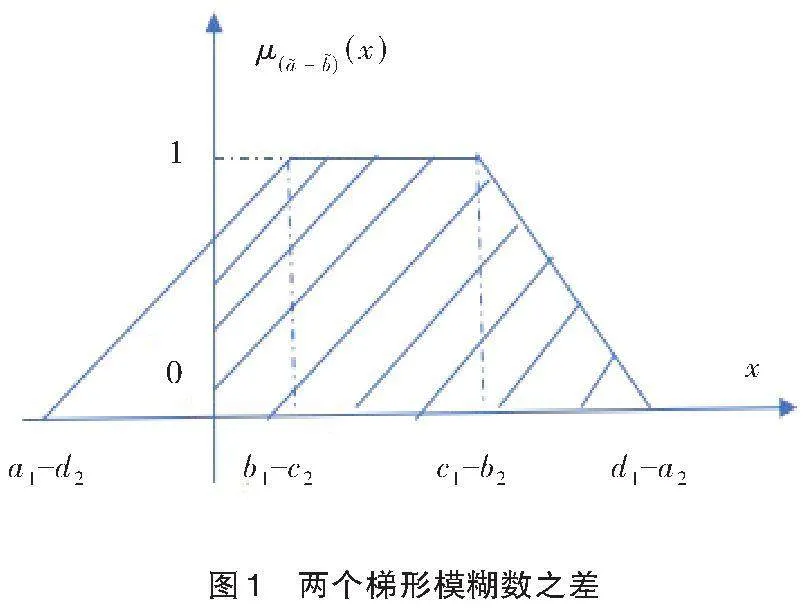
注1 定义3的实质是把差模糊数对应的图形落在[x]轴的正半轴部分作为依据。

注2" （1） 一个梯形模糊数与一个三角模糊数（或区间数）之差还是一个梯形模糊数。

（2） 一个三角模糊数与一个区间数之差也是一个梯形模糊数。反之，一个区间数与一个三角模糊数之差也是一个梯形模糊数。

（3） 一个三角模糊数与另一个三角模糊数之差仍是一个三角模糊数；一个区间数与另一个区间数之差仍是一个区间数，此结论显然。

2.2" 理论分析

定理1 当定义3中的两个梯形模糊数退化为定义5中的两个区间数时，定义3与定义5是等价的。

证明：当[a1gt;b2]时，有[a1-b2gt;0]，由于[a1lt;b1，a2lt;b2]，则有[b1-a2≥a1-b2gt;0]，因此有[α=max （0，a1-b2]）=[a1-b2]， [β=max0，b1-a2=b1-a2]，从而有

当[a2gt;b1]时，有[a1-b2≤b1-a2lt;0]，则有[α=β=0]，从而有

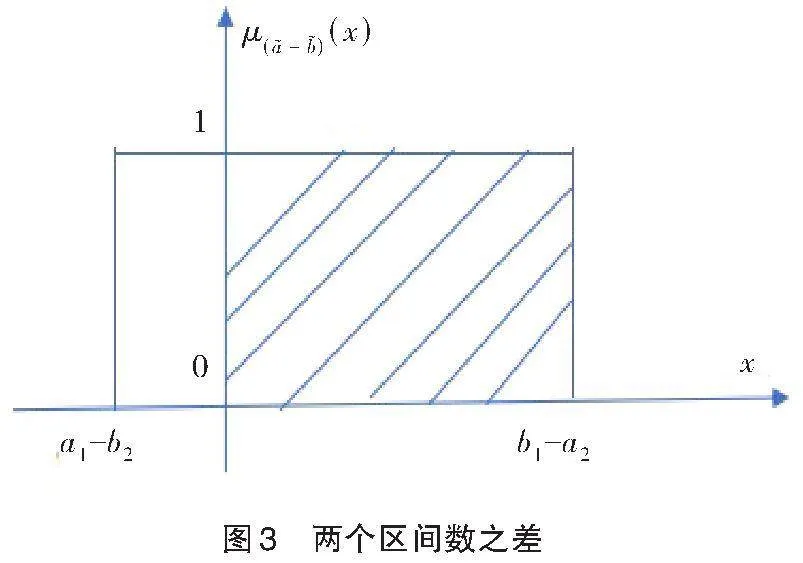
当[a2≤b1，a1≤b2]时，即两个区间数有交叉时，相当于图3情形。此时可由公式（3）有

因此，定理1的结论成立。

注3" （1）由定理1可知，对于区间数的情形，定义3与定义5等价，同样也与文献[4]所列举的其他7个公式等价，这也说明利用区间数减法运算法则所给出的定义3是合理的。

（2）从计算复杂度上看，定义3和定义5几乎没什么差别，但是定义3却能从几何意义上看出定义的思想实质，即在直角坐标系下，差模糊数所对应非负部分的面积与整个差模糊数所对应的面积之比。

（3）定义3更重要的价值是把差运算法则应用到三角模糊数和梯形模糊数。正是由于定理1的启发，我们可以给出能同时满足区间数、三角模糊数、梯形模糊数的比较公式，甚至能比较这三种模糊数混合的情形。

3 多个模糊数的排序方法

对于区间数有如下事实：

证明：我们可以用公式（4）来证明。

由（5）式可知

由（6）式可知

由（7）式+（8）式可得

这说明本方法仅仅保证定性次序，但不能保证定量次序。

定理2虽然是针对区间模糊数而言，但是区间模糊数是特殊的梯形模糊数，所以我们有理由认为这种使用可能度来决定次序对于三角模糊数和梯形模糊数也是不具有定量传递性。

关于梯形模糊数和三角模糊数的这种特性，我们尚无法严格证明，不过可以通过一个例子来验证（仅以梯形模糊数为例）。

例如：三个梯形模糊数

李德清等在文献[4]中指出，对于多个区间数利用可能度两两比较判断矩阵，若采取行和法比较会产生逆序现象，因为可能度两两比较判断矩阵不是模糊一致性矩阵。定理2也体现了两个模糊数的可能度比较不满足模糊一致性。

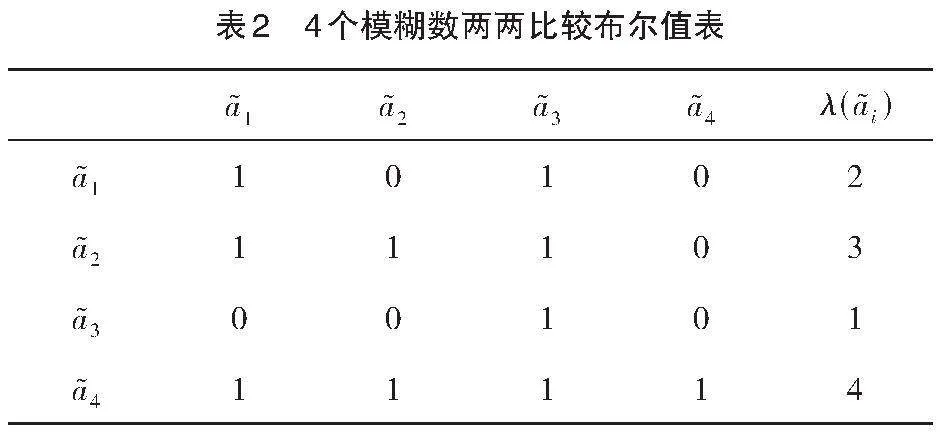
对于多个区间数排序时，为了克服逆序现象，李德清等[4]提出了布尔矩阵法。

因此在比较多个模糊数（梯形模糊数、三角模糊数或区间数）次序时，利用可能度两两比较判断矩阵，为了避免产生逆序现象，下面我们也采用布尔矩阵法来排序。

4 算 例

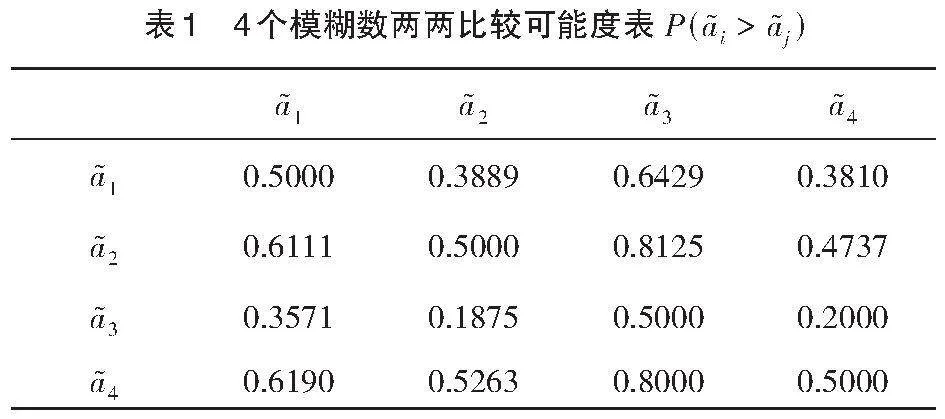
例1 试比较以下4个模糊数的次序：

例1显示了本方法可以对区间数、三角模糊数和梯形模糊数的混合情形进行比较，证明了本方法的可行性。

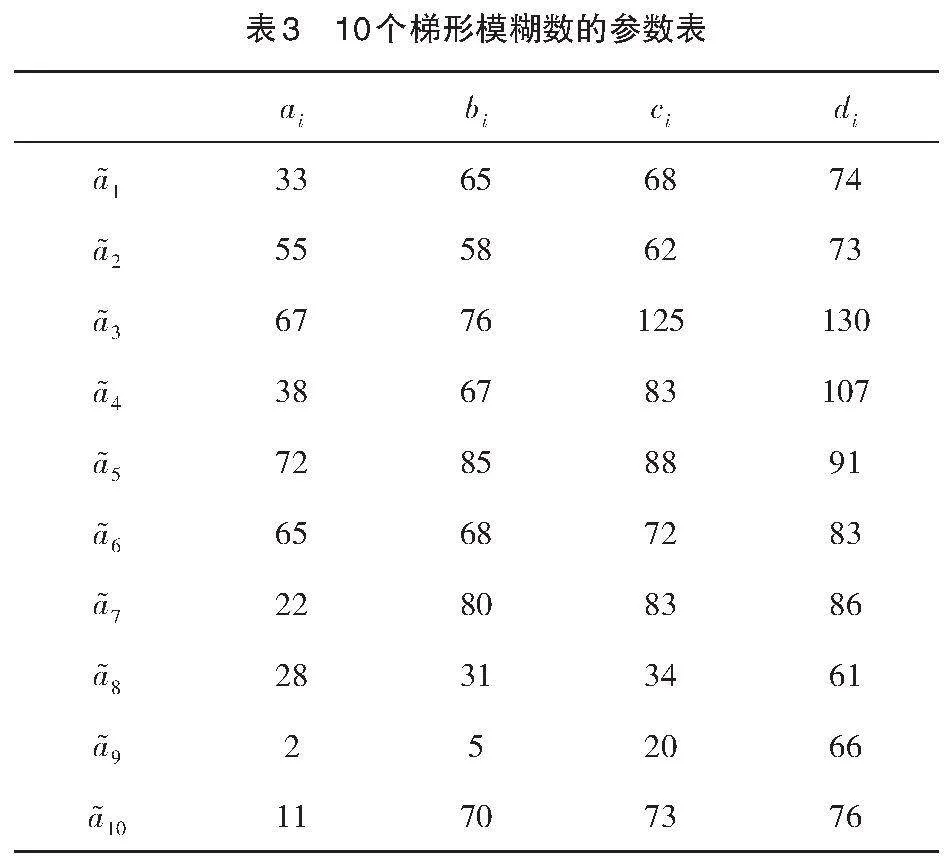
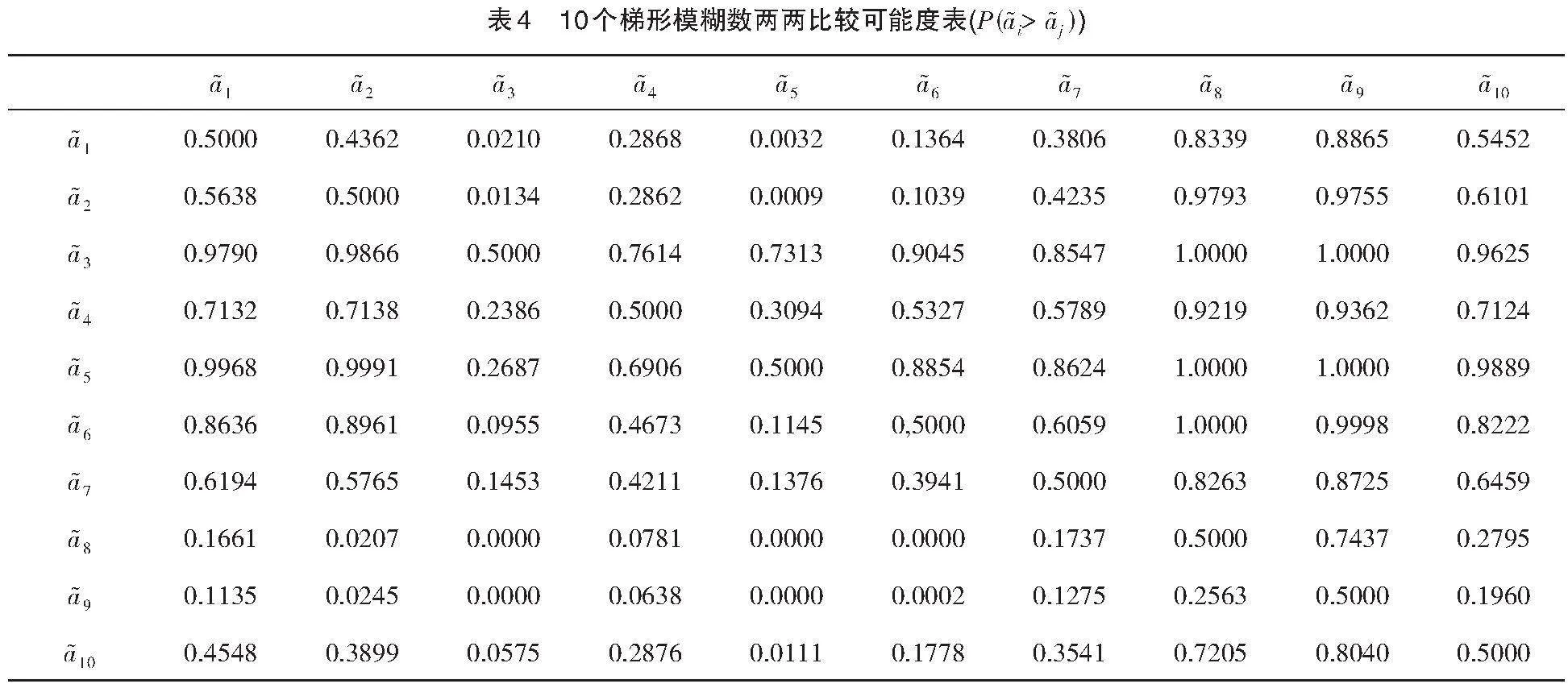
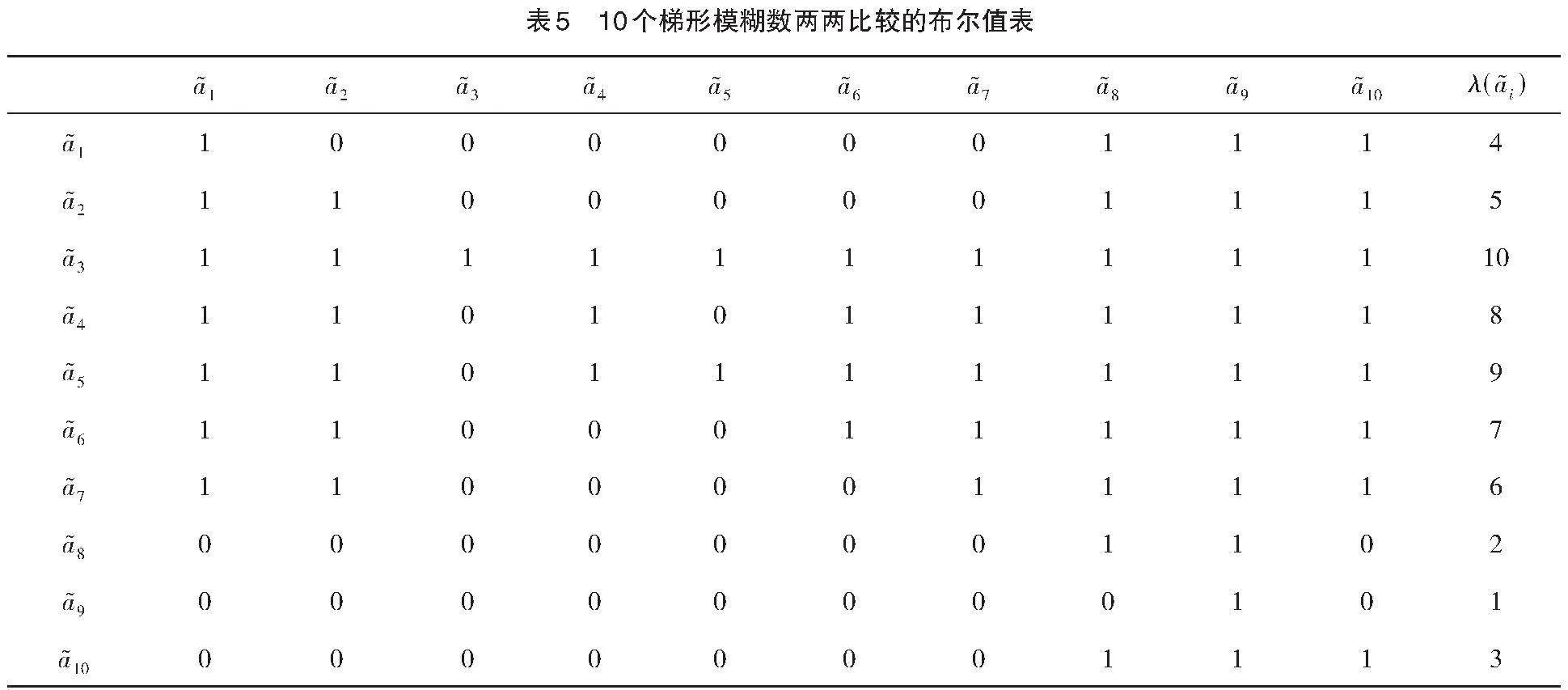
例2 试比较文献[14]中的10个梯形模糊数的次序，数据信息见表3，计算的结果如表4和表5所示。

因此最终的结果为

了，这充分显示了本方法的优效性。

5 结束语

本文首先利用两个模糊数之间的减法运算法则提出可能度的概念，分析了这种可能度的性质，并给出理论根据；其次，利用可能度给出比较两个模糊数的次序的方法，并利用布尔矩阵法对多个模糊数进行排序；最后，通过与文献[14]的比较，显示出本方法的优效性。总之，该方法计算公式几何意义明确，易于形象记忆和理解，计算简单，区分度强，便于掌握，因此适用面更广。

参考文献：

［1］ZHANG Z.Logarithmic least squares approaches to deriving interval weights，rectifying inconsistency and estimating missing values for interval multiplicative preference relations[J].Soft Computing，2017，21（14）：3993-4004.

［2］高峰记.可能度及区间数综合排序[J].系统工程理论与实践，2013，33（8）：2033-2040.

［3］SENGUPTA A，PAL T K.On comparing interval numbers：a study on existing ideas，in fuzzy preference ordering of interval numbers in decision problems[M].Berlin：Springer Berlin Heidelberg，2009：25-37.

［4］李德清，韩国柱，曾文艺.基于布尔矩阵的区间数排序方法[J].控制与决策，2016，31（4）：629-634.

［5］WANG Y M，YANG J B，XU D L，et al.On the centroids of fuzzy numbers[J].Fuzzy Sets Systems，2006，157（7）：919-926.

［6］ABBASBANDY S，ASADY B.Ranking of fuzzy numbers by sign distance[J].Information Science，2006，176（16）：2405-2416.

［7］YU V F，CHI H T X，WEN S C.Ranking fuzzy numbers based on epsilon-deviation degree[J].Applied Soft Computation，2013，13（8）：3621-3627.

［8］WANG Y J.Ranking triangle and trapezoidal fuzzy numbers based on the relative preference relation[J].Applied Mathematical Modelling，2015，39（2）：586-599.

［9］CHAI K C，TAY K M，LIM C P.A new method to rank fuzzy numbers using Dempster-Shafer theory with fuzzy targets[J].Information Sciences，2016，346（2）：302-317.

［10］GU Q，XUAN Z.A new approach for ranking fuzzy numbers based on possibility theory[J].Journal of Computational and Applied Mathematics，2017，309（3）：674-682.

［11］HESAMIAN G，BAHRAMI F.Credibility theory oriented preference index for ranking fuzzy numbers[J].Iranian Journal of Fuzzy Systems，2017，14（6）：103-117.

［12］HIERRO A F R L，ROLDN C，HERRERA F.On a new methodology for ranking fuzzy numbers and its application to real economic data，in theme：fuzzy intervals[J].Fuzzy Sets Systems，2018，353（1）：86-110.

［13］王钦，李贵春.梯形模糊数的有序表示及中心平均排序方法，运筹与管理[J].2017，26（5）：130-136.

［14］DOMBI J，J T.Ranking trapezoidal fuzzy numbers using a parametric relation pair[J].Fuzzy Sets and Systems，2020，399（1）：1-23.

［15］ZHANG Z M.Deriving the priority weights from trapezoidal fuzzy reciprocal preference relations based on uncertainty ratio and geometric mean[J].Journal of Intelligent amp;Fuzzy Systems，2017，33：1083-1095.

［16］齐春泽.基于梯形模糊MULTIMOORA的混合多属性群决策方法[J].统计与决策，2019，35（5）：41-45.

A New Method for Sorting Trapezoidal Fuzzy Numbers

Abstract： The issue of the size of fuzzy numbers has always been a hot research topic. With the deepening of research， fuzzy numbers have evolved from interval numbers to triangular fuzzy numbers， and then to trapezoidal fuzzy numbers. This article proposes a new trapezoidal fuzzy number sorting method. This method is based on two trapezoidal fuzzy number subtraction rules， which provide the concept of possibility degree through definite integral operation， and use the size of possibility degree and Boolean matrix method to sort multiple fuzzy numbers. The feasibility of this method is demonstrated through a numerical example， and its effectiveness and superiority are demonstrated through comparison with the recent literature method. This method can not only compare the order of different types of fuzzy numbers， but also has simple calculation， strong discriminative power， and broad application prospects.

Key words： trapezoidal fuzzy number; possibility degree; Boolean matrix; sort