二维半线性波动方程的能量稳定的Galerkin方法超收敛分析

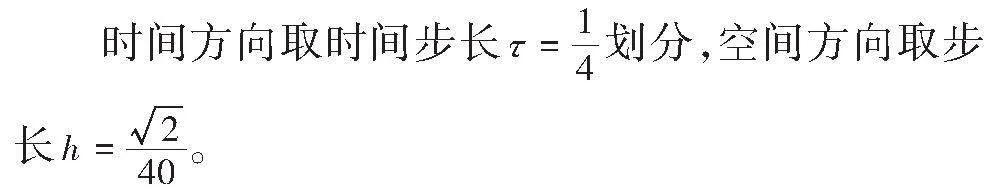
摘 要：文章研究了一类半线性波动方程的能量稳定的全离散Galerkin方法的超收敛误差估计。首先，分析了数值格式解的唯一性和稳定性。其次，利用矩形网格上双线性元的特殊性质以及插值算子和Ritz算子在[H1]-范数下的超逼近的估计，得到了超逼近的结果。再次，借助于插值后处理技术得到了[H1]-范数下的全局超收敛的结果。最后，通过数值实验验证了理论分析的正确性。

关键词：半线性波动方程，能量稳定的全离散格式，超收敛误差估计

中图分类号：O242.21" 文献标识码：A" "文章编号：1007 - 9734 （2024） 04 - 0098 - 08

0 引 言

在许多数学和物理问题的研究中，半线性波动方程都是一类重要的数学模型。本文研究了一类半线性波动方程的能量稳定的全离散方法Galerkin的超收敛误差估计。

考虑如下的半线性波动方程[1-3]：

[utt（x， t）-Δu（x， t）+ut（x， t）+f（u）=0，（x， t）∈Ω×（0，T]] （1）

[u（x，0）=u0（x）， ut（x， 0）=u1（x）， x∈Ω] （2）

[u（x， t）=0，" " " （x， t）∈∂Ω×（0，T] ] （3）

其中，[Ω⊂R2]是一个矩形区域，其边界为[∂Ω]，[x=（x1，x2）]，且[f（u）=u3] 。

波动方程的数值方法已经得到广泛研究， 包括有限差分法[4-7]、有限元法[8-16]及间断Galerkin方法[17-19]。特别地，文献[4]研究了两种有限差分格式，得到了离散[H1]-范数的最优误差估计；文献[5]给出了一个求解二维二阶非齐次线性双曲方程的三阶紧致差分格式；文献[8]讨论了含有瞬时系数的二阶双曲方程的一个有限元分裂外推法；文献[10]使用Galerkin方法研究了一个二阶线性双曲方程，并得到了[L∞（L2）]范数的最优误差估计。此外，文献[11]使用连续和离散Galerkin方法，建立了不同边界条件下的一个广义波动方程的[L2]范数的最优误差估计；文献[12]提出了一类二阶双曲问题的一个[H1]-Galerkin混合有限元方法；文献[13]和文献[14]通过使用二重网格混合有限元方法研究非线性双曲方程，并得出了最优误差估计；文献[15]和文献[16]使用Galerkin有限元方法得到了非线性波动方程的超收敛误差估计。然而，这些全离散格式都不是能量稳定的。文献[17-19]分别研究了二阶波动方程的间断Galerkin方法，并得到了相应的最优误差估计。

目前，关于半线性波动方程的能量稳定的有限元方法的超收敛误差分析的研究还少见报道。本文的主要目的是研究问题（1）—（3）的能量稳定的全离散Galerkin格式的超收敛误差估计。文章其余部分安排如下：第2部分介绍了一些预备知识和引理。第3部分研究了能量稳定Galerkin格式的全离散超收敛误差估计。第4部分通过一些数值结果验证了理论分析的正确性。

在本文中，我们使用标准的记号[Wm，p（Ω）]来表示Sobolev空间，其上的范数和半范数分别记为[||⋅||][m，p]和[|⋅|m，p]（参见文献[20]），相应的[L2]内积记为[⋅，⋅]。我们用[C]（带下标或不带下标）代表一般正常数，它不依赖于[n]（时间层）、[h]（空间尺寸）及[τ]（时间步长），并且在不同地方代表不同的值。

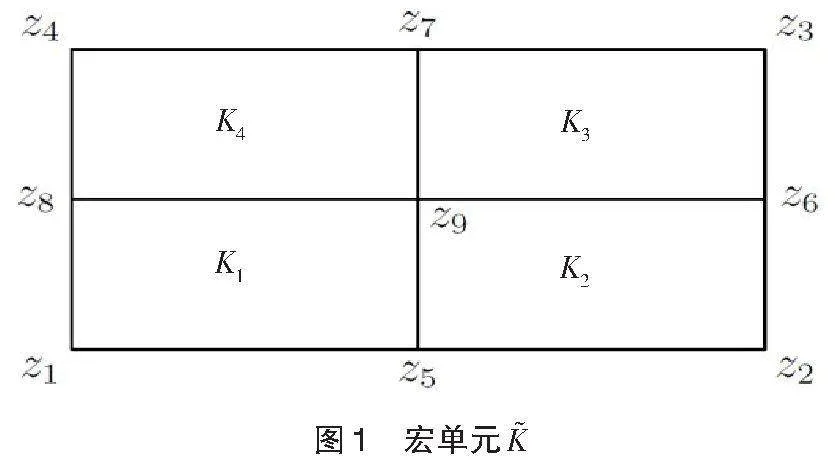
1 预备知识和引理

此外，在文献[23]中已经证明了算子[I2h]有如下

3 数值结果

在这一节中，我们给出两个数值例子来验证理论分析的正确性。

例1[误差和收敛阶]

在计算过程中，我们令[Ω=0，1×0，1]，并且选取最终时间[T=1.0]。考虑半线性非齐次波动双曲方程：

[utt-Δu+ut+u3=g（t，x，y），" （x，y）∈Ω， 0lt;t≤T]。

设函数[g]以及与如下精确解相对应的初始条件和边界条件：

[u（t，x，y）=exp（-t）sin（2πx）sin（2πy）]。

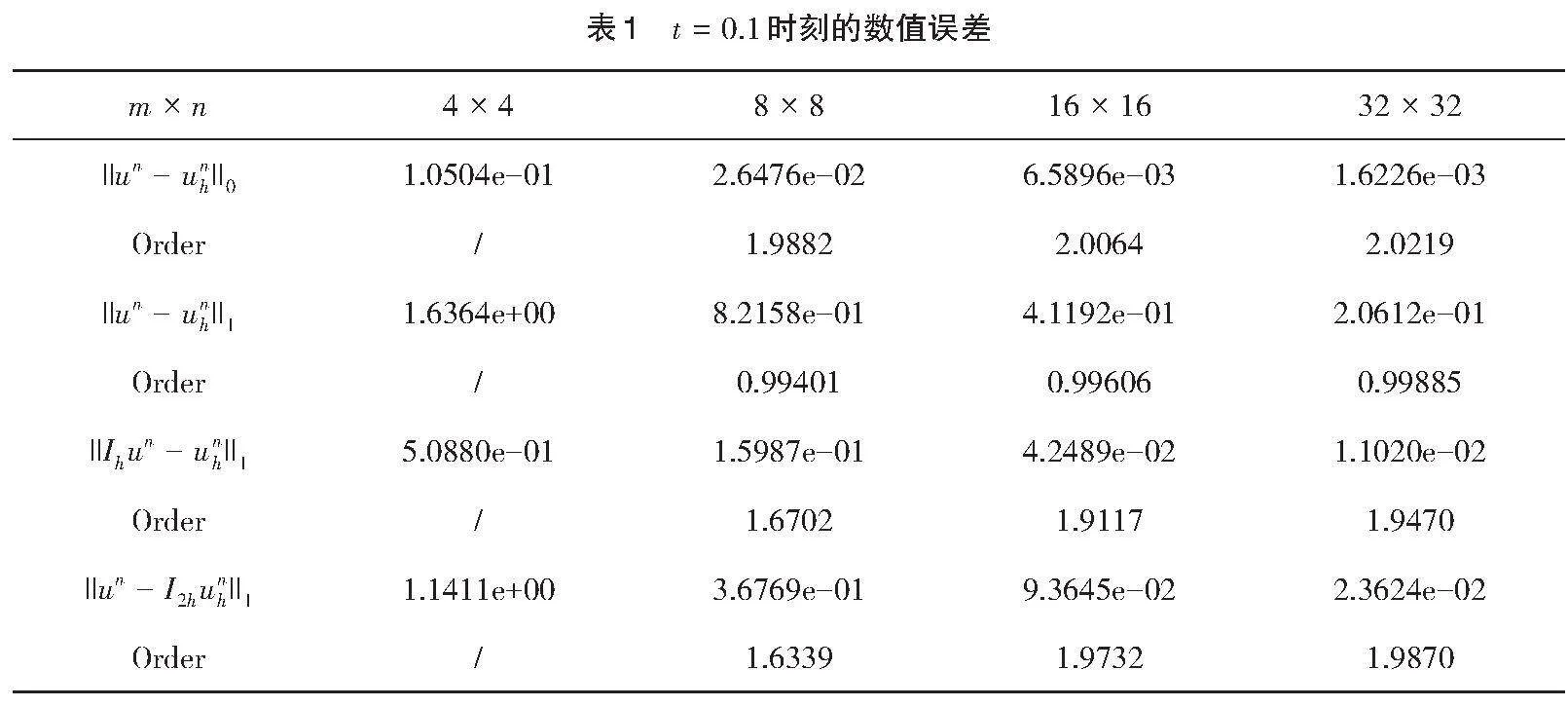
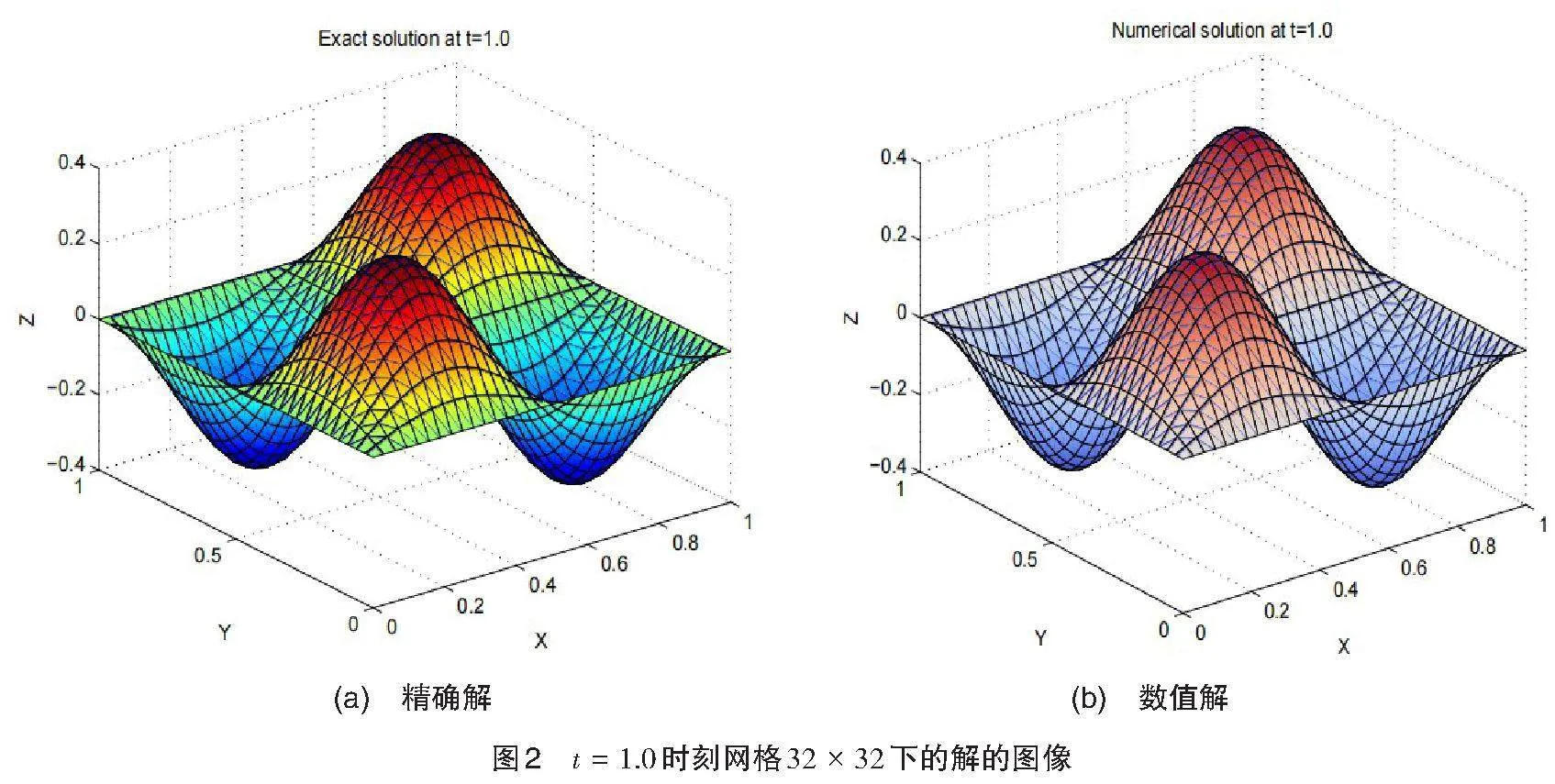
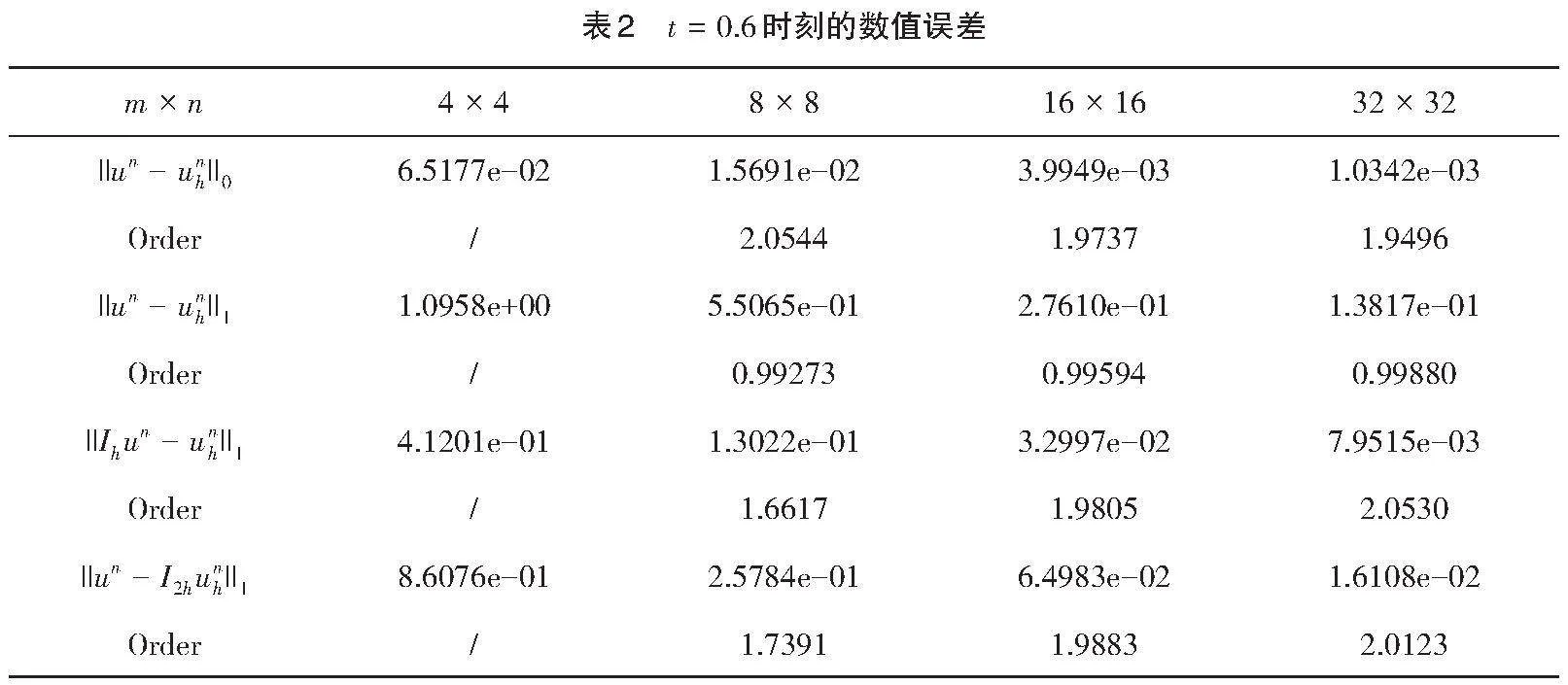
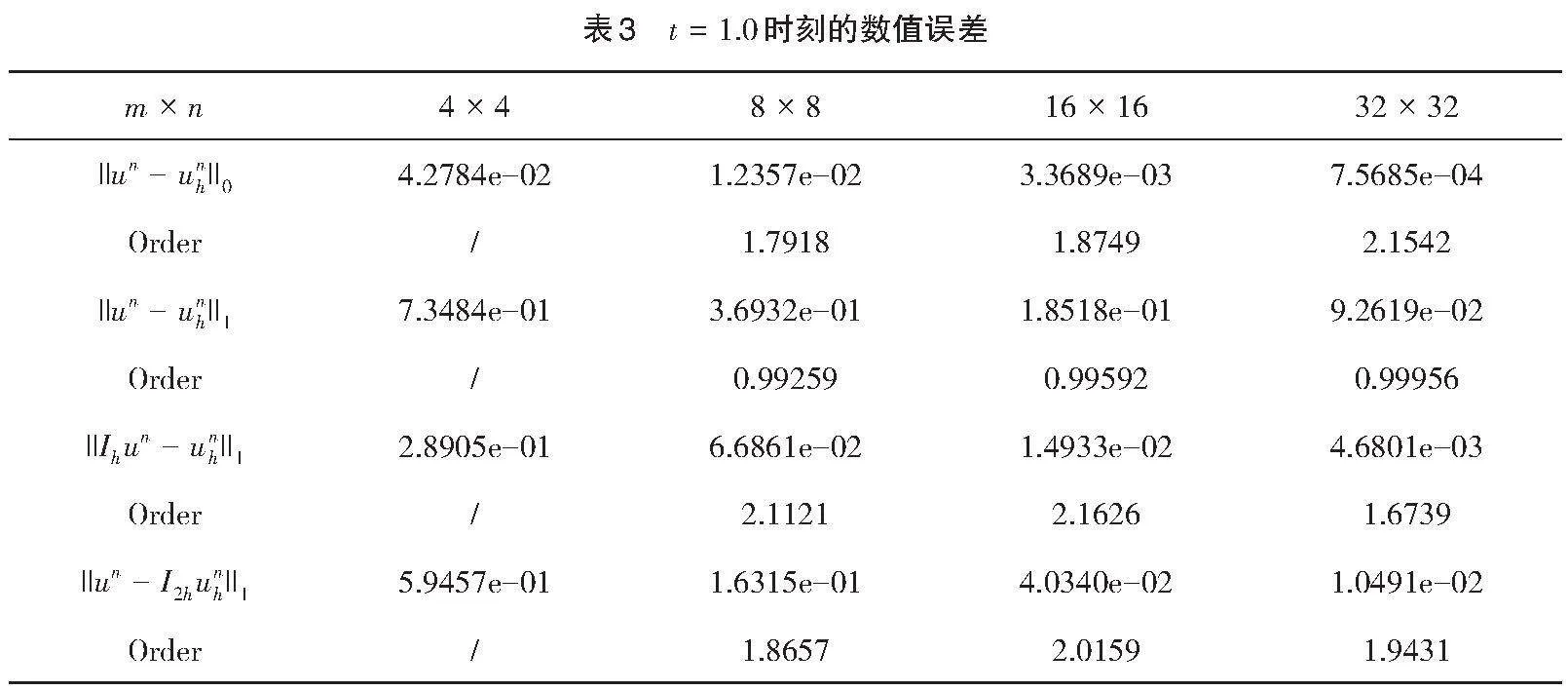
在表1—表3中分别给出了在[t=0.1，][0.6，][1.0]处的[||un-unh||0，][||un-unh||1，][||Ihun-unh||1]和[||un-I2hunh||1]的数值误差。可以看到，数值结果和理论分析结果吻合的很好，收敛阶分别为[O（h2），][O（h），][O（h2）]和[O（h2）]。与此同时，图2中给出了精确解和数值解在[t=1.0]在网格剖分为[32×32]的图像，也表明了数值解与精确解十分接近。

例 2[不增加的离散能量[4]]

考虑如下非线性波动方程

[utt-Δu+ut+u3=0， （x，y）∈Ω， 0lt;t≤T=10]，

初始条件

[u（x，y，0）=sin（2πx）sin（2πy）， ut（x，y，0）=-sin（2πx）sin（2πy）， （x，y）∈Ω]。

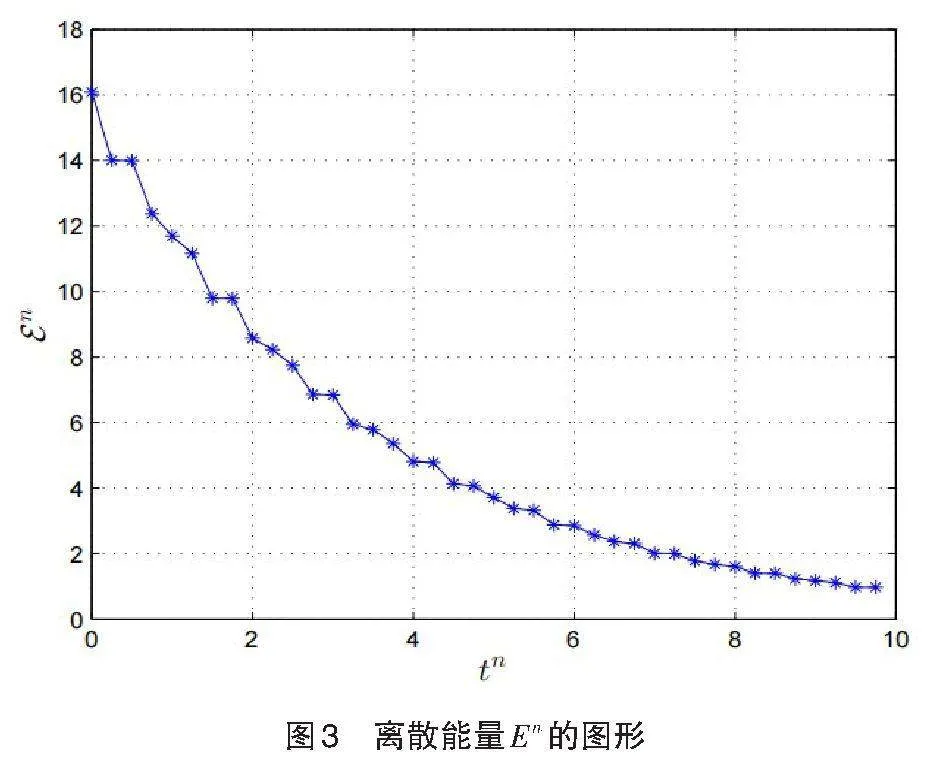
图3中给出了式（8）—式（10）在不同时间层[tn]下的离散能量。可以看出数值格式保持了离散能量的不增加特性，这与理论分析相一致。

综上，本文研究了一类半线性波动方程的能量稳定的全离散Galerkin方法，利用矩形网格上双线性元的特殊性质，插值算子和Ritz算子在[H1]-范数下的超逼近的估计以及从能量稳定性质所得到的数值解的能量范数有界性，得到了精确解的插值和数值解之间的超逼近的结果。进一步，借助插值后处理技术，得到了精确解和后处理解之间的超收敛的误差估计结果。最后通过两个数值例子验证了理论分析的正确性。本文主要考虑的是二维的情形，以后的工作可以研究三维的情形并拓展到较为复杂的问题中去。

参考文献：

［1］BALL J M.On the asymptotic behavior of generalized processes，with applications to nonlinear evolution equations[J].Journal of Differential Equations，1978，27（2）：224-265.

［2］MATSUMURA A.On the asymptotic behavior of solutions of semi-linear wave equations[J].Publications of the Research Institute for Mathematical Sciences ，Kyoto University，1976，12：169-189.

［3］ARRIETA J M，CARVALHO A N，HALE J K.A damped hyperbolic equation with critical exponent[J].Communications in Partial Differential Equations，1992，17（5-6）：841-866.

［4］ACHOURI T.Finite difference schemes for the two-dimensional semilinear wave equation[J].Numerical Methods for Partial Differential Equations，2019，35：200-221.

［5］DING H，ZHANG Y.A new fourth-order compact finite difference scheme for the two-dimensional second-order hyperbolic equation[J].Journal of Computational and Applied Mathematics，2009，230（2）：626-632.

［6］LIAO H，SUN Z.A two-level compact ADI method for solving second-order wave equations[J].International Journal of Computer Mathematics，2013，90（1）：1471-1488.

［7］WANG S，KREISS G.Convergence of summation-by-parts finite difference methods for the wave equation[J].Journal of Scientific Computing，2017，71：219-245.

［8］HE X M，LU T.A finite element splitting extrapolation for second order hyperbolic equations[J].SIAM Journal of Scientific Computing，2009，31（6）：4244-4265.

［9］BASSON M，VAN RENSBURG N F J.Galerkin finite element approximation of general linear second order hyperbolic equations[J].Numerical Functional Analysis and Optimization，2013，34（9）：976-1000.

［10］BAKER G A，.Error estimates for finite element methods for second order hyperbolic equations[J].SIAM Journal on Numerical Analysis，1976，13（4）：564-576.

［11］DUPONT T.[L2]-estimate for Galerkin methods for second order hyperbolic equations[J].SIAM Journal on Numerical Analysis，1973，10：880-889.

［12］PANI A K，SINHA R K，OTTA A K.An [H1]-Galerkin mixed method for second order hyperbolic equations[J].International Journal of Numerical Analysis and Modeling，2004，1（2）：111-129.

［13］WANG K Y，CHEN Y P.Two-grid mixed finite element method for nonlinear hyperbolic equations[J].Computers amp; Mathematics with Applications，2017，74（6）：1489-1505.

［14］WANG K Y，CHEN Y P.Analysis of two-grid discretization scheme for semilinear hyperbolic equations by mixed finite element methods[J].Mathematical Methods in the Applied Sciences，2018，41（9）：3370-3391.

［15］WEI Y F，SHI D Y.Superconvergence analysis of a two-grid method for nonlinear hyperbolic equations[J].Computers amp; Mathematics with Applications，2020，79（10） ：2846-2855.

［16］SHI D Y，WANG R.Unconditional superconvergence analysis of a two-grid finite element method for nonlinear wave equations[J].Applied Numerical Mathematics，2020，150：38-50.

［17］HAN W M，HE L M，WANG F.Optimal order error estimates for discontinuous galerkin methods for the wave equations[J].Journal of Scientific Computing，2019，78：121-144.

［18］GROTE M J，SCHTZAU D.Optimal error estimates for the fully discrete interior penalty DG method for the wave equation[J].Journal of Scientific Computing，2009，40：257-272.

［19］GROTE M J，SCHNEEBELI A，SCHOTZAU D.Discontinuous Galerkin finite element method for the wave equation[J]，SIAM Journal on Numerical Analysis，2006，44（6）：2408-2431.

［20］ADAMS R，FOURNIER J.Sobolev Spaces[M].Amstrdam：Academic Press，2003.

［21］THOMEE V.Galerkin finite element methods for parabolic problems[M].Berlin Heidelberg：Springer-Verlag，2006.

［22］BRENNER S，SCOTT L.The mathematical theory of finite element methods[M].New York：Springer，2002.

［23］LIN Q，LIN J F.Finite element mthods：accuracy and improvement[M].Beijing：Science Press，2006.

［24］KESAVAN S.Topics in functional analysis and application[M].New Age International Publishers，2008.

［25］SHARMA N，KHEBCHAREON M，SHARMA K，et al.Finite element galerkin approximations to a class of nonlinear and nonlocal parabolic problems[J].Numerical Methods for Partial Differential Equations，2016，32（4）：1232-1264.

Superconvergence Analysis of an Energy-Stable Galerkin Method for

Two-Dimensional Semilinear Wave Equation

Abstract： In this paper， an implicit fully-discrete energy-stable Galerkin scheme is proposed and investigated for the semilinear wave equation. Firstly， the unique solvability and the stability of the numerical solution are studied. Then， in terms of the special property of the bilinear element on the rectangular mesh and the supercolose estimate between interpolation operator and Ritz operator in [H1]-norm， the global superconvergence result in [H1]-norm is obtained using a post-processing technique. Finally， numerical experiment is performed to support the theoretical findings

Key words： Semilinear wave equation； energy-stable fully-discrete scheme； superconvergence error estimate