直观表征促理解，紧扣本质促迁移

【摘 要】运算能力主要是指根据法则和运算律进行正确运算的能力。运算能力主要体现在三个方面，其中之一就是能够明晰运算的对象和意义，理解算法与算理之间的关系。在乘法的运算教学中，教师要引导学生理解数和运算所表示的意义，经历算理和算法的探索过程，体会数的运算与数的组成之间的密切联系，感悟运算本质的一致性，培养运算能力和推理意识等核心素养，进而发展学生的数学思维。文章以人教版数学三年级下册第四单元中“两位数乘两位数（不进位）”笔算乘法为例，探究如何基于单元整体视角下，聚焦运算本质，提升学生的运算能力。

【关键词】运算本质 直观表征 运算能力 推理意识

一、课前思考

乘法运算的本质就是计数单位的累加，除了能用口诀直接得到结果的以外，其他的都是把数按计数单位进行拆分，先分别求积，再求和，也就是“先分后合”。同时，这也是乘法分配律的本质所在，如32×13=32×（10+3）=32×10+32×3=（30+2）×10+（30+2）×3=30×10+2×10+30×3+2×3。而不同位数的笔算乘法，只是竖式中积的层数不同，方法是完全可以迁移的。

“两位数乘两位数（不进位）笔算乘法”可以说是整个乘法运算的关键课。学生在这之前已经学习了“表内乘法”、“多位数乘一位数”和“两位数乘两位数口算乘法”，之后将在四年级学习“三位数乘两位数”。本课重在让学生利用转化思想，将两位数乘两位数转化成两位数乘整十数和两位数乘一位数，来理解算理、迁移算法，同时又重在建构竖式双层积的模型，为后续多位数乘多位数的学习实现自主迁移。

通过学生访谈与问卷，教师发现大部分学生知道算式的结果，却不能正确地表征算理和算法，出现了第二层积写错位置的现象，究其原因还是学生没有理解每一步的意义。教材在编写时，特意加入了点子图这一直观模型，它既能简洁形象地表征数和算式的含义，让学生从不同的角度充分地感悟“分”的多样化及“合”的一致性，又能帮学生理解算理和竖式计算方法，感悟到乘法运算中根据计数单位拆数，再将相同计数单位累加的本质。

因此，本课的教学目标定为：

1.经历自主探究“两位数乘两位数（不进位）笔算乘法”的过程，借助点子图理解算理、掌握算法，发展运算能力和推理意识。

2.在操作、分类、比较、归纳中优化算法，培养学生将新知转化为旧知解决问题的迁移类推能力。

3.感受知识与知识之间、知识与生活之间的联系，培养学生自主迁移的能力，激发学生的学习兴趣。

教学重点：理解两位数乘两位数的算理，掌握竖式计算方法。

教学难点：理解竖式第二步积的位置书写，体会乘法运算的本质。

二、课堂实践

（一）情感熏陶，提出问题

师：今年的4月23日，是第29个世界读书日，主题是“阅读推动未来”。我们学校的读书活动也如火如荼地开展，同学们读经典、诵美文，都沉浸在了书香的世界里。

课件视频播放学生读书活动并出示图片，如图1。

师：为了丰富图书品种，学校决定购买一批图书。

根据这些信息，你能提出什么数学问题？

生：一共买了多少册？

【思考】教师以世界读书日为背景，在潜移默化中引导学生树立读书意识。接下来从学生真实的生活问题引入，激发学习兴趣。

（二）自主探索，尝试解决

1.表征原型，理解算式本质

师：要解决这个问题怎么列式？

生：14×12。

师：为什么用乘法呢？

生：因为每套书有14册，有12套，也就是求12个14是多少，用乘法比较简便。

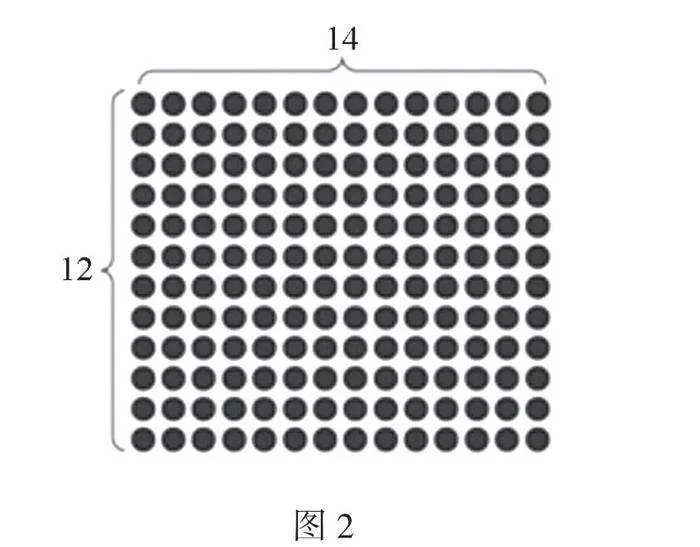
师：你对乘法的意义理解得真好。如果我们用一个圆点来表示一册书，那这一行就是14册，有12行，要求一共有多少册，也就是要求12个14的和。

课件动态演示，如图2。

（师板书：14×12）

【思考】数的运算要基于理解数的结构和运算的意义，教师借用点子图帮助学生理解14×12的本质是求14个12的和是多少或者是12个14的和是多少，直观表达乘法的意义，为后续揭示乘法运算本质埋下伏笔。

2.勾连旧知，感悟转化思想

师：这是一道两位数乘两位数的算式。结合我们之前学习多位数乘一位数、两位数乘整十数的经验，用什么方法来帮助我们解决这个新问题？

生1：我觉得可以用转化的方法，把其中的一个两位数拆分成一位数加一位数，再来算。

生2：也可以转化成整十数加一位数。

【思考】转化思想在乘法运算中有着至关重要的作用，通过唤醒学生已有的学习经验，将“先分后合”的方法迁移到两位数乘两位数，促进学生思维能力的发展。

3.直观操作，探究算法多样

师：从旧知识中想到了解决新问题的方法，真了不起。现在请同学们独立思考，试着用横式写出计算方法，并用点子图把自己的方法表示出来，再和小组成员说一说自己的想法。

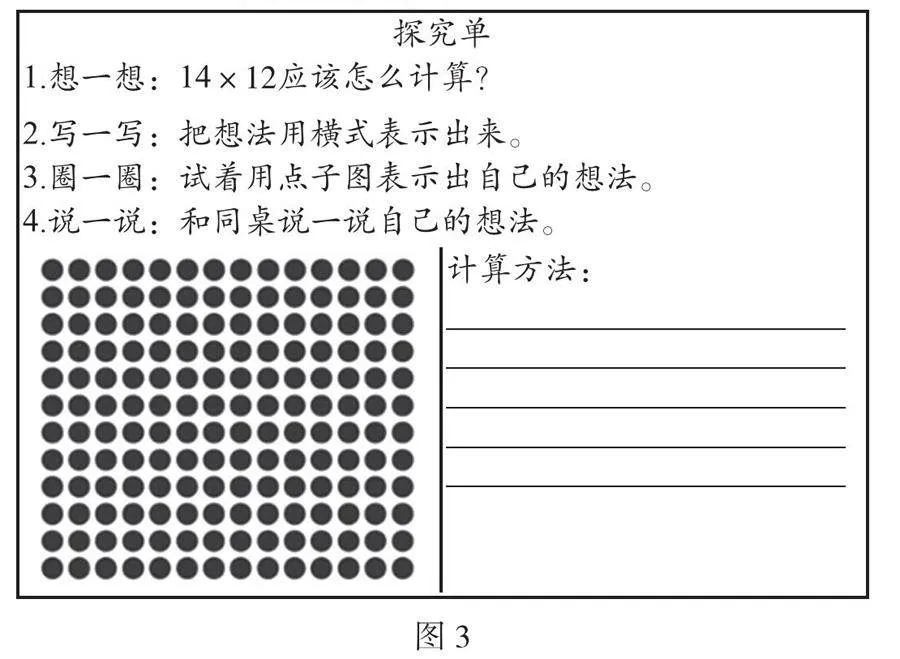
课件出示探究要求，如图3。

探究单

1.想一想：14×12应该怎么计算？

2.写一写：把想法用横式表示出来。

3.圈一圈：试着用点子图表示出自己的想法。

4.说一说：和同桌说一说自己的想法。

计算方法：

学生自主探究，组内交流，教师巡视指导并收集作品。

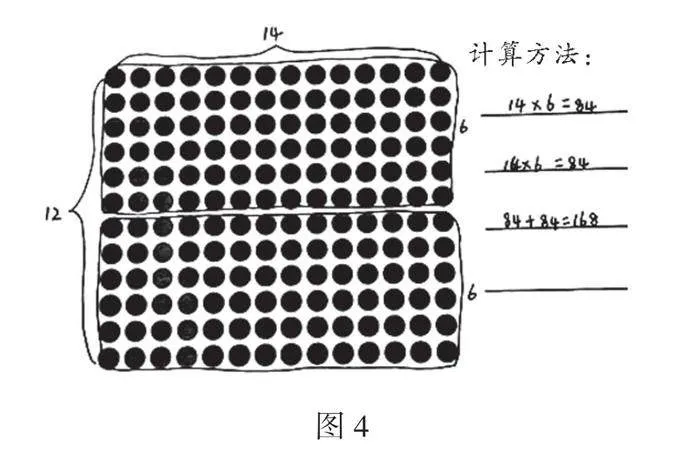
生1：我把12分成了2个6。上面圈的部分表示6个14，下面也有6个14，都可以用14×6=84来计算，再把两个部分合起来，可以用84+84=168，也可以直接用乘法84×2=168。

展示学生作品1，如图4。

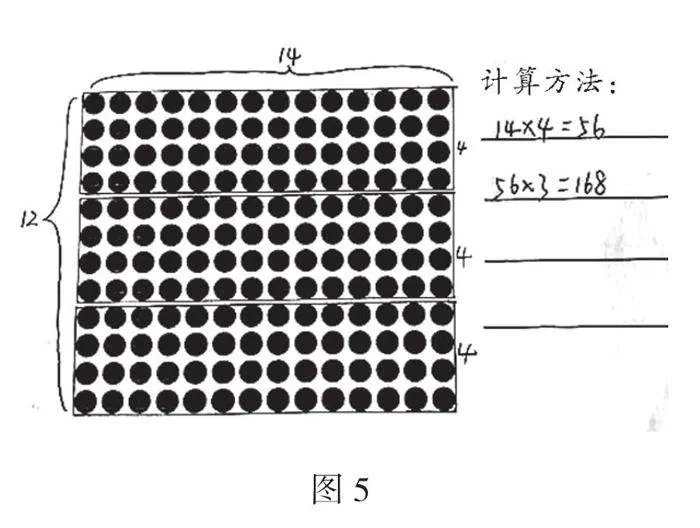
生2：我把12平均分成了3个4。先算14×4=56，表示每份点子图都是56，一共有3个56，直接用乘法56×3=168。

展示学生作品2，如图5。

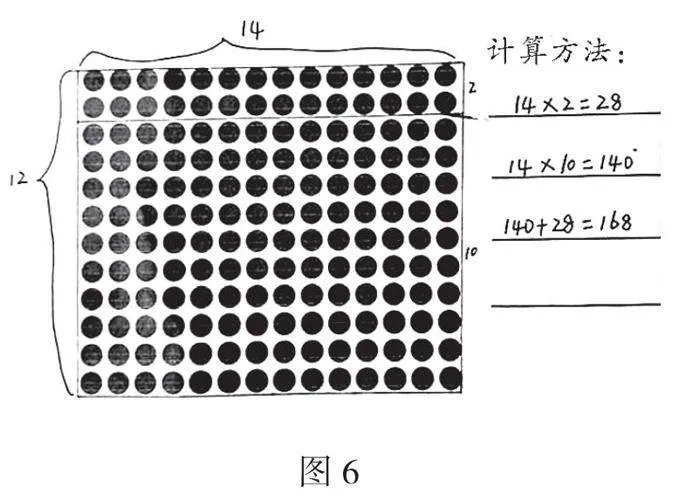
生3：我把12分成2和10。先算14×2=28，表示2个14，也就是上面这2行点子图的数量。再算14×10=140，表示10个14，就是下面10行点子图的数量。最后算28+140=168，表示一共有12个14。

展示学生作品3，如图6。

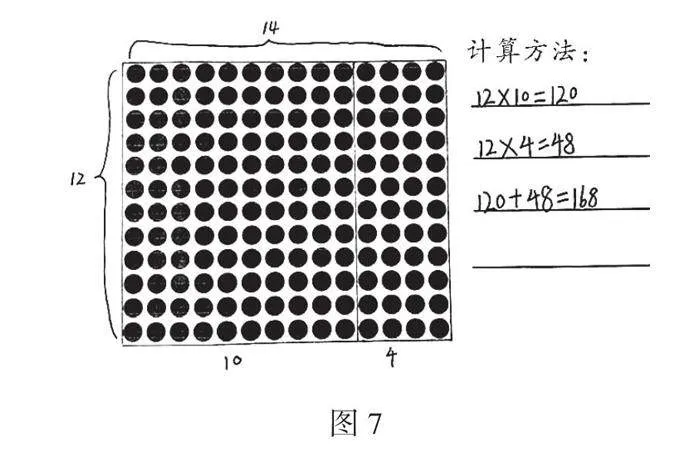
生4：我是把每行的14拆成了10和4。先算左边的12个10，12×10=120，再算右边的12个4，12×4=48，最后合起来120+48=168，也算出了14×12的结果。

展示学生作品4，如图7。

师：同学们不仅找到了这么多的计算方法，还能通过点子图说明其中的道理，真是了不起。

【思考】通过横式写一写、点子图圈一圈、小组说一说等系列活动，放手让学生从不同的角度充分地感悟“分”的多样化，达到了横式表征、图形表征、语言表征的一致性，在数形结合中帮助学生直观充分地理解“先分后合”的算理。

4.对比辨析，优化计算方法

师：对比这4种方法，它们有什么相同和不同之处吗？

生：它们都用到了“先分后合”的方法。作品1和作品2是把12平均分，作品3和作品4是把其中一个数分成了一个整十数和一个一位数。

师：为什么要先分后合呢？

生：通过分一分，我们可以把两位数乘两位数，转化成以前学过的两位数乘一位数或是乘整十数这样的旧知识。

师：说得真好！带着转化的思想去学习，我们可以轻松地解决很多的新问题。在这些方法中，你最喜欢哪种方法？为什么？

生1：我最喜欢作品1表示的方法，14×6=84，84+84=168，平均分两份，容易口算。

生2：我不太同意你的看法。如果是13×23，这两个数都没有办法平均分得到整数。

师：发现这个问题了吗？（生点头）

生3：我喜欢作品3表示的方法，14×2+4×10= 168。因为两位数乘整十数非常容易口算，更重要的是任何一个两位数，我们都可以把它拆成一个整十数和一个一位数。

生4：我也喜欢作品3表示的方法和作品4表示的方法。多位数乘一位数，我们是根据计数单位把数进行拆分，所以我觉得两位数乘两位数应该也是这样。

师：在同学们的辩论中，我们清楚地看到了，根据计数单位把两位数乘两位数转化成两位数乘整十数、两位数乘一位数来计算，是一种基本的计算方法，它与笔算也有着重要的联系。

【思考】通过关键问题，让学生对比辨析不同算法的特点，引导学生从计数单位的角度去理解运算的意义，打通了学生对数的意义与运算一致性的理解，发展了学生的运算能力和推理意识，为建构竖式模型奠定基础。

5.图式结合，建构竖式模型

师：现在，你能试着用竖式来计算14×12吗？在学习单上写一写。

学生自主完成，教师巡视收集典型作品展示，如图8。

方法一（1号） 方法二（2号）

师：对比这些方法，你觉得哪种方法能够清楚地表示出计算的过程呢？

生：我觉得是2号作品，它这里有两层，能看得出先算了2×14=28，再算10×14=140，最后再算28+140=168。

师：（问1号作品学生）你觉得呢？

生1：确实比我的更清楚，能看出每一步是怎么计算的。

师：那我们请2号作品的创作者，结合点子图来说说自己的计算过程。

生2：我把12分成10和2，第一步算点子图的上面这个部分，14×2=28，把积写在第一层；第二步算点子图的下面这个部分，14×10=140，把积写在第二层，最后把两层的积加起来是168。

生3：老师，我还有发现。我们在计算时，做了4个乘法，第一个是2乘4得8；第2个是2乘1得2，但这里的1表示一个10，所以是20；第三个是1乘4得4，1表示一个十，所以是40，4写在十位上；最后一个是1乘1得1，这两个1都表示一个十，所以是100，1要写在百位上。

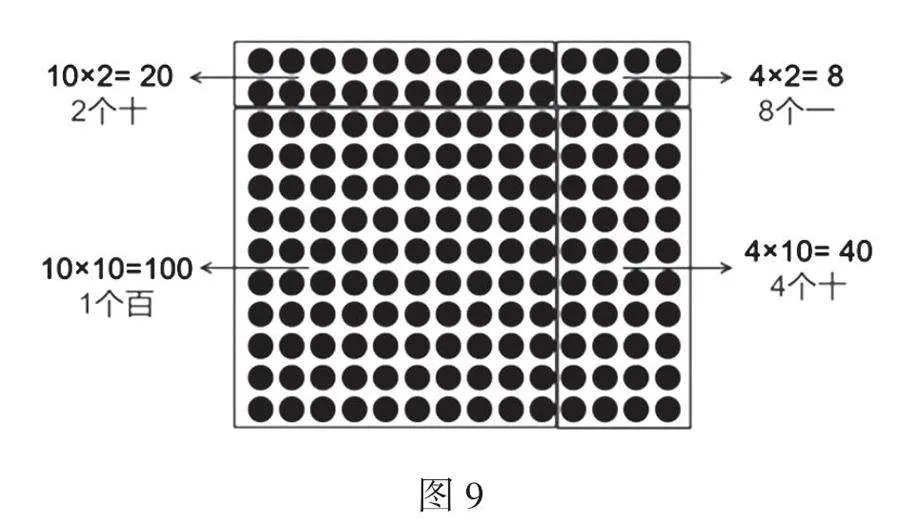
师：把两位数乘两位数转化成了4个表内乘法，再根据计数单位写在相应的数位上。你能这么深入地理解，真是太棒了！为了让同学们看得更明白，你能在点子图上把这四个部分分别圈出来吗？

学生圈写，如图9。

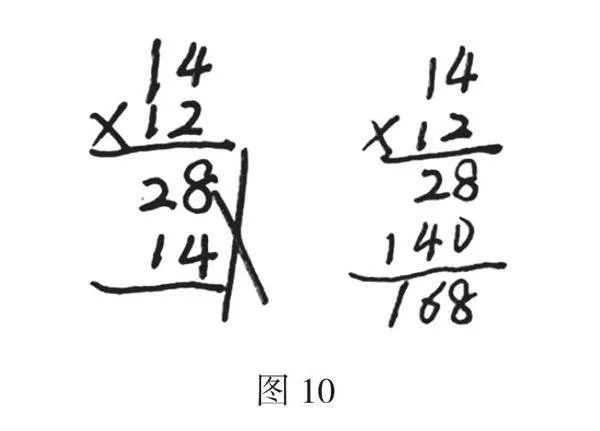
师：谢谢你用图让我们清楚地看到了过程。老师还收集到了一幅作品，我想请作者来说说自己的想法（指学生作品错误处，图10）。

生5：（不好意思）我也是先算14×2=28，在算14×10=140时，我把它直接想成14×1=14，写积的时候没有对齐数位，就发现自己错了。

师：很善于发现问题。那要提醒大家注意什么？

生5：就是计算第二步的时候，要记住这个1表示的是1个十，1个十乘4个一，得到的是4个10，这个4要写在十位上。1个10乘1个10得到的是1个百，这个1要写在百位上，也就是说乘出来是什么单位，就要写到什么数位上。

师：针对他修改后的写法，大家有没有什么疑问的地方？

生6：140的个位上没有写0，可以吗？

生5：我觉得个位上的0写不写都不会影响结果，因为1写在百位上了，4写在了十位上，借助数的位置我们可以清楚地看出这是14个10。

生7：加号也可以省略不写吗？

生5：数学不是讲究简洁美吗？除法中的减号可以省略不写，那乘法中的加号也可以省略不写吧！

师：在同学们的一问一答中，我们的知识不断地完善。正如同学们所说的那样，我们在笔算两位数乘两位数时，第二个乘数十位上的数乘第一个乘数的积，个位上的0可以省略不写，但数位一定要对齐。我们一起把这个过程写一下，你们说，我来写。

教师板书学生计算过程。

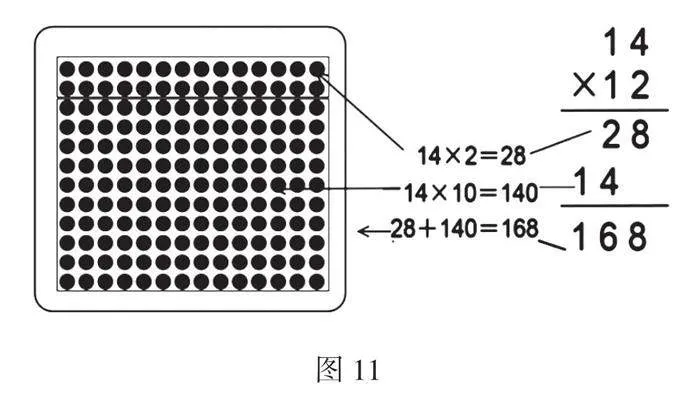
师：观察竖式计算、横式计算和相应的点子图（手指板书），它们之间有什么关联？和同桌交流交流。（图11）

学生同桌交流，教师巡视，学生汇报。

生：它们表示的意思相同，算法也是一样的，都是把12分成10和2，先算两个乘法，最后算加法。

师：说得真好。笔算其实就是把3道口算综合在一个竖式中，这样计算就更加简便了。结合到例题，谁能说一说每一步分别表示的是什么意思？

生：14乘2表示的是两套书的册数是28，14乘10表示的是10套书的册数是140，28加140表示是的12套书的册数是168。

【思考】在学生借助点子图充分理解两位数乘两位数的算理后，顺势让学生尝试创造出体现计算过程的竖式。再借助点子图，让学生将竖式计算中的每一步与图形同步表征，促进了学生对两层积位置的理解。通过对比点子图、横式与竖式三者之间的关联，将抽象的数与直观的形紧密结合，帮助学生形象地建构起两位数乘两位数形象的竖式模型。

（三）巩固应用，拓展深化

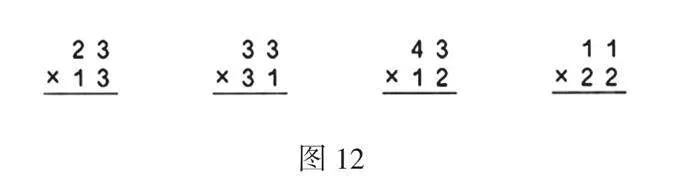
1.做一做

学生独立完成（图12），代表板演反馈，集体订正。

2.算一算，填一填

学校举行读书节成果汇报展示，图13是三年级全体学生的列队图。

三年级一共有多少名学生？

生独立计算后，反馈交流发现竖式中的每一步都可以在图中表示出来。

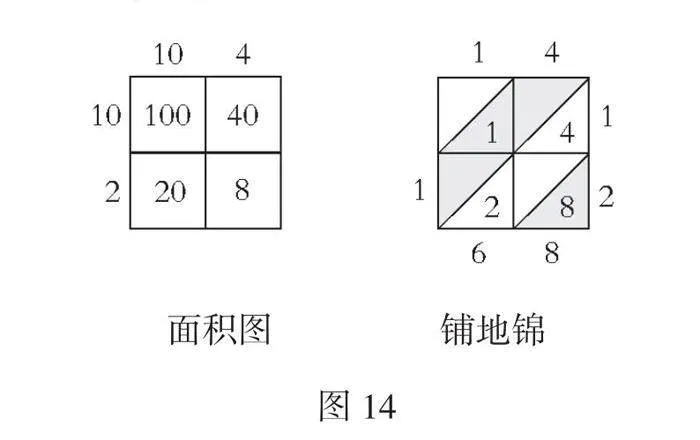
3.介绍面积图和铺地锦

师：通过点子图和表格，我们直观形象地理解了乘法运算“分与合”的算理。除了这些方法，我们的古人还会用这样的面积图和“铺地锦”的方法来计算两位数乘两位数，我们古人把这种方法叫作铺地锦。见图14。大家看看，它是怎么做的？

生：它也把数按计数单位拆分开，分别计算有几个一，几个十和几个百。

师：是的，看来同学们对乘法有了非常深的感悟。

【思考】通过基本笔算、点子图说理练习和数学文化的拓展，学生再次清晰了两位数乘两位数的算法，强化了“几个几和几个几相乘得几个几”的算理。

（四）梳理总结，类推迁移

师：谁再说一说这节课有什么样的收获？

学生汇报。

师：对比两位数乘两位数和两位数乘一位数，它们之间有什么相同和不同之处？

迁移：根据这些学习经验，这样的三位数乘两位数213×32怎么计算？学生课后探究。

【思考】教师通过往前看多位数乘一位数，往后看三位数乘两位数，凸显了乘法运算本质算理的理解，突出了知识的结构化认识，引导学生认清知识本质，迁移类推来解决新问题，进而培养了学生的推理意识，提高了运算能力。

三、课后思考

小学生运算能力的培养，不能盲目地认为熟能生巧，而要站在学生的立场，从单元整体视角的高度，引导学生经历有形有思的探究过程，体会运算本质及运算之间的关联，这样才能对运算进行融通理解，形成合理的认知结构。

一要关注知识的本质理解，实现结构化的认识。计数单位是任何运算教学的核心概念，教师在教学时要充分研究数和运算的意义，从计数单位的角度去引导学生理解“法”与“理”。在本课教学时，结合三年级学生的特点，教师充分借助点子图，让学生经历了14×12的意义表征、算法多样化的探究、以图说算理、竖式建模与第二层积的位置理解、横竖式和点子图的对比等活动，让学生理解了两位数乘两位数的本质是把数拆分，分别进行几个几、几十个几、几百个几累加的过程，也就是计数单位的累加，连通了“位”与“值”，帮助学生实现了乘法运算的结构化认识。

二要注重知识的前后关联，感悟运算的一致性。史宁中教授说，培养运算能力，就是要让学生学会从已知到未知。教学中，通过唤醒学生已有的两位数乘整十数、两位数乘一位数的学习经验，感悟到“转化”思想的重要性。课堂小结处，教师让学生回顾两位数乘两位数和两位数乘一位数的同与不同之处，再拓展多位数乘多位数，为学生不断打通乘法运算之间的壁垒，找寻到知识的关联之处和生长之源，使学生深切地感悟到运算的一致性，推动了学生运算能力和推理意识等核心素养的发展。