基于Lamb波的复合材料多损伤定位方法研究

摘 要：针对航空航天用碳纤维增强树脂基复合材料多损伤问题，研究一种损伤方向算法与椭圆轨迹算法相结合的损伤定位方法。首先，根据Lamb波在板中的传播特性，提出一种基于PZT结的损伤方向算法，运用方向算法找到Lamb波在损伤位置发生散射后的若干传播方向，再通过传播方向的交点来实现多损伤位置的初步判定。其次，运用椭圆轨迹算法，实现多损伤位置的进一步判定。最后，在碳纤维增强树脂基复合材料薄板上对该方法进行实验验证，选用希尔伯特黄变换的信号处理技术实现对损伤散射信号到达时间的提取。实验结果表明，该损伤定位方法能够对复合材料多损伤位置进行有效定位。

关键词：复合材料；多损伤定位；方向算法

中图分类号：TH145.9；TB332" 文献标识码：A" 文章编号：1007 - 9734 （2024） 03 - 0030 - 09

0 引 言

碳纤维复合材料具有高强度、高模量、良好的抗疲劳性能和抗腐蚀性能等特点，被广泛应用于航空航天领域［1］。近年来，随着国防工业的快速发展，碳纤维复合材料在飞机上的应用越来越多，使用的部位从尾翼、舵面等次承力结构扩展到机翼等主承力结构，结构形式从简单的梁式、板式结构向夹层结构、整体复杂结构方向发展。航空用复合材料及制件的快速发展，给无损检测技术提出了更高的要求［2］。Lamb波是在具有自由边界的固体板或层状结构中传输的一种弹性导波，由于其本身的传播特性，如沿传播路径衰减小、能量损失小、传输距离远等，成为现行复合材料超声无损检测领域研究的重要手段。

判定无损检测手段是否有效，关键是看能否实现缺陷的有效定位。国内外研究人员对基于Lamb波的材料缺陷定位算法展开了大量研究。李娟娟等［3］采用椭圆与双曲线混合定位算法进行损伤定位研究，绘制了损伤的横纵坐标概率统计图，并且借助图像融合方法得出了损伤概率成像图，实现了脱粘缺陷的准确定位；韩伟等［4］提出了一种无须材料尺寸、力学参数、频散特性的双曲线定位算法，可较精确地定位出复合材料中存在的缺陷；王高平等［5］提出了一种采用Lamb波时间反转聚焦原理结合椭圆法定位的方法，通过采集Lamb波反转聚焦信号得到时间延时，计算出损伤与传感器的距离，再通过几何定位得到损伤位置。HAMEED等［6］在椭圆轨迹算法的基础上，提出了一种基于归一化Lamb 波信号连续小波变换（CWT）的损伤估计方法，利用基于联合和妥协融合方案的损伤指数构建综合损伤图像。XU等［7］提出了一种基于椭圆环的非线性Lamb 波不完全群速度匹配的三维结构微裂纹定位与成像方法。以上这些研究都是针对单一损伤问题展开的，但在实际应用中复合材料多损伤判定问题也较为普遍。因此，如何快速、准确地实现对多损伤位置的判定也是复合材料损伤定位检测需要解决的问题。

本文以碳纤维增强树脂基复合材料板为研究对象，提出一种压电传感器（Piezoelectric transducers，PZT）结方向算法，并与椭圆轨迹算法结合，对多损伤缺陷位置进行定位检测。通过合理布置PZT结的位置和数量，运用HHT变换提取出损伤散射信号，得到各PZT 接收损伤散射信号的时间，进一步得到PZT结中各PZT的时间差和位移差，找到遇损伤发生散射的 Lamb 波方向，并结合方向交点与椭圆方程得到损伤位置。

1 损伤判定原理

1.1" PZT结方向算法

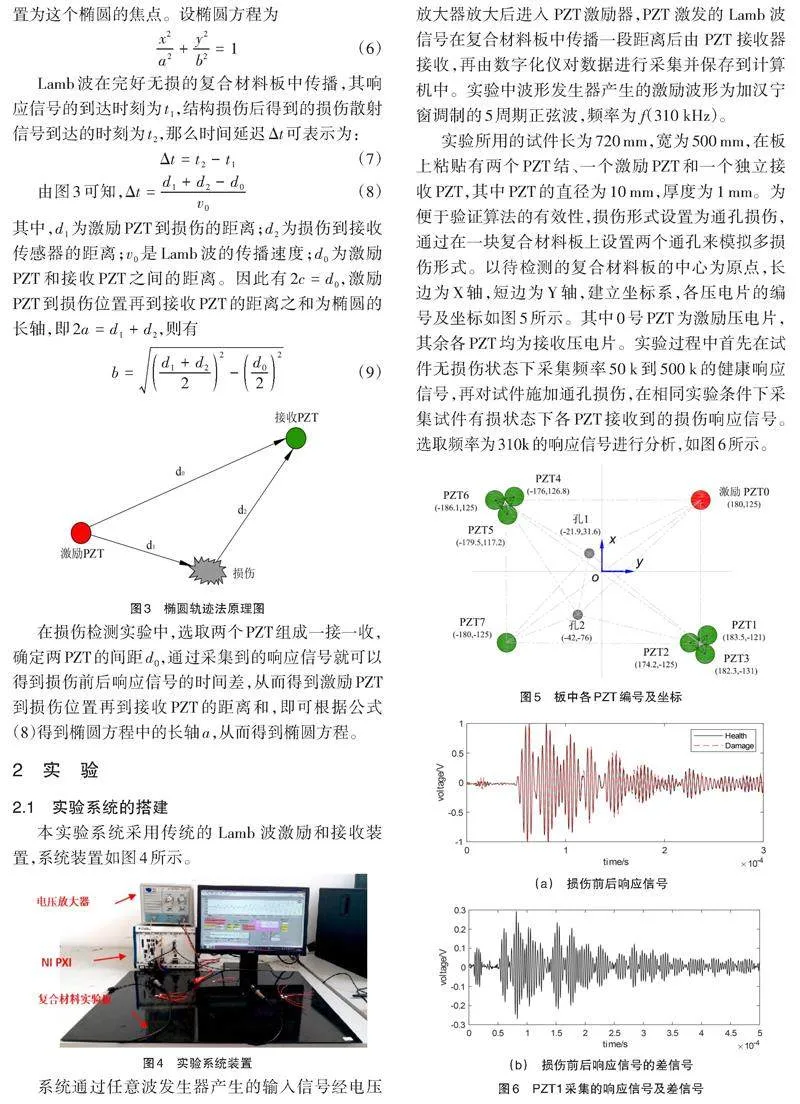
由于Lamb波在板中传播时遇到损伤会产生散射［8-10］，因此可以在其中一个散射方向的合适位置布置一定数量的PZT［11-12］，PZT能够接收到板中经由损伤位置散射过来的某一方向Lamb波信号，当得到两个及以上损伤散射方向时，将会产生方向交点，而方向交点即为损伤位置。为确定损伤的准确位置，至少需要两束由损伤位置散射而来的Lamb波响应信号，如图1所示。通过求取得到[θ1]、[θ2]的值，即可得到损伤散射的其中两个方向，从而初步确定损伤位置。

本文采用的是由三个PZT组成的PZT结，PZT结中的三个PZT呈三角形布置，各PZT之间的间距不宜过大，最小为两个PZT的半径之和。损伤方向算法的提出是基于一种几何原理，当Lamb波散射时，到达PZT的中心位置，此时经过PZT的中心可得到损伤方向的切线。由于PZT结中的各PZT间距与Lamb波传播距离相比数值较小，因此可将整个PZT结作为一个整体。每个PZT接收到的Lamb波散射方向近似相同，在散射方向未知的情况下，可以先找到其中两个PZT接收到散射信号的方向的切线，再作其垂线即可得到损伤方向。具体算法如下：

以一个PZT结为例，复合材料层合板尺寸为[l×w]，以板的中心为原点，长边为x轴，短边为y轴，建立坐标系，PZT结中的各PZT中心坐标为[xi，yi] [i=1，2，3]。选取各PZT结中的其中一个PZT为基准压电片，其坐标为[xb，yb]，损伤信号到达各PZT的时间为[ti]，到达基准PZT的时间为[tb]，以一个PZT结为例，则有[Δti=ti−tb]，由Lamb波在板中传播的速度[v]可得[Δli=Δti⋅v]，以基准PZT的中心为圆心，[Δli]为半径画圆，如图2所示。分别过PZT结中另外两个PZT的中心作圆1、圆2的切线[m1]、[m2]，记[m1、m2]的斜率分别为[k1、k2]，理想状态下有[m1]//[m2]，结合波的传播理论，则损伤信号的方向为与[m2]和[m1]垂直的方向。现依据各点在坐标系中的位置可推导出损伤方向的计算表达式。

由分析可得，以基准PZT的中心为圆心的圆方程为：

[x−xb2+y−yb2=Δli2] （1）

过第[i]个PZT中心作圆切线方程为：

[ki−y−kixi+yi=0] （2）

点到直线的距离公式为：

[d=Ax0+By0+CA2+B2] （3）

基准PZT中心到过点1的圆切线距离为[Δli]，得：

[Δli=kxb−yb−kxi+yik2+1] （4）

[ki=xb−xiyb−yi±Δlixb−xi2+yi−yb2−Δli2xb−xi2−Δli2] （5）

由公式（5）可以看到，在计算各切线方向方程的斜率k时，会同时得到两个不同的斜率值，利用PZT结中两PZT对应的切线斜率应相等，可以排除掉不相等的两斜率值。设损伤方向为[kd]，则有[kd⋅ki=−1]。由此，即可得出一个PZT结所对应的损伤散射信号的方向。同理，多个PZT结则会计算出多个损伤方向，通过计算每个PZT结接收到的不同损伤方向，得出各损伤方向的交点，即可判定损伤位置。

1.2" 椭圆定位

假设波恒定传播，根据采集到的响应信号可以得到Lamb波从激励PZT到达接收PZT的传播时间，激励PZT到损伤位置的距离和接收PZT到损伤位置的距离二者之和恒定，因此，损伤可能在的位置就形成了一个椭圆的轨迹［13］，接收PZT和激励PZT所在位置为这个椭圆的焦点。设椭圆方程为

[x2a2+y2b2=1] （6）

Lamb波在完好无损的复合材料板中传播，其响应信号的到达时刻为[t1]，结构损伤后得到的损伤散射信号到达的时刻为[t2]，那么时间延迟[Δt]可表示为：

[Δt=t2−t1] （7）

由图3可知，[Δt=d1+d2−d0v0] （8）

其中，[d1]为激励PZT到损伤的距离；[d2]为损伤到接收传感器的距离；[v0]是Lamb波的传播速度；[d0]为激励PZT和接收PZT之间的距离。因此有[2c=d0]，激励PZT到损伤位置再到接收PZT的距离之和为椭圆的长轴，即[2a=d1+d2]，则有

[b=d1+d222−d022] （9）

在损伤检测实验中，选取两个PZT组成一接一收，确定两PZT的间距[d0]，通过采集到的响应信号就可以得到损伤前后响应信号的时间差，从而得到激励PZT到损伤位置再到接收PZT的距离和，即可根据公式（8）得到椭圆方程中的长轴[a]，从而得到椭圆方程。

2 实 验

2.1 实验系统的搭建

本实验系统采用传统的 Lamb 波激励和接收装置，系统装置如图4所示。

系统通过任意波发生器产生的输入信号经电压放大器放大后进入 PZT激励器，PZT 激发的 Lamb 波信号在复合材料板中传播一段距离后由 PZT 接收器接收，再由数字化仪对数据进行采集并保存到计算机中。实验中波形发生器产生的激励波形为加汉宁窗调制的5周期正弦波，频率为 f（310 kHz）。

实验所用的试件长为720 mm，宽为500 mm，在板上粘贴有两个PZT结、一个激励PZT和一个独立接收PZT，其中PZT的直径为10 mm，厚度为1 mm。为便于验证算法的有效性，损伤形式设置为通孔损伤，通过在一块复合材料板上设置两个通孔来模拟多损伤形式。以待检测的复合材料板的中心为原点，长边为X轴，短边为Y轴，建立坐标系，各压电片的编号及坐标如图5所示。其中0号PZT为激励压电片，其余各PZT均为接收压电片。实验过程中首先在试件无损伤状态下采集频率50 k到500 k的健康响应信号，再对试件施加通孔损伤，在相同实验条件下采集试件有损状态下各PZT接收到的损伤响应信号。选取频率为310k的响应信号进行分析，如图6所示。

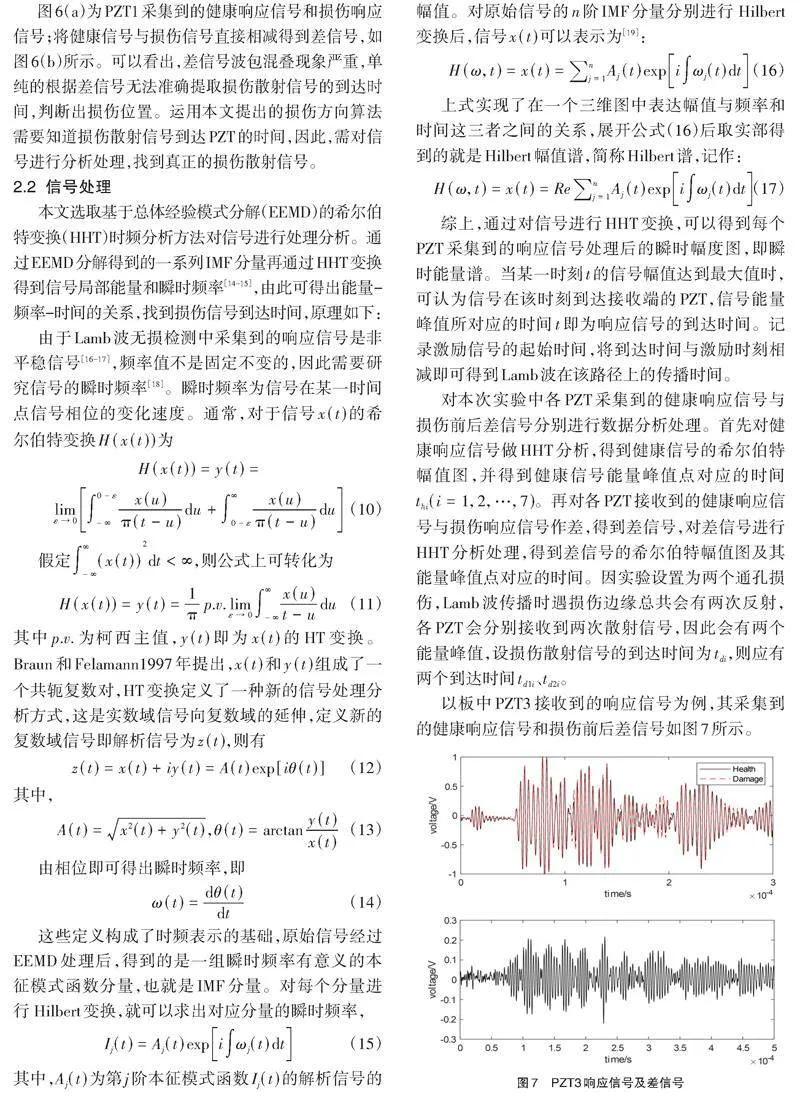
图6（a）为PZT1采集到的健康响应信号和损伤响应信号；将健康信号与损伤信号直接相减得到差信号，如图6（b）所示。可以看出，差信号波包混叠现象严重，单纯的根据差信号无法准确提取损伤散射信号的到达时间，判断出损伤位置。运用本文提出的损伤方向算法需要知道损伤散射信号到达PZT的时间，因此，需对信号进行分析处理，找到真正的损伤散射信号。

2.2" 信号处理

本文选取基于总体经验模式分解（EEMD）的希尔伯特变换（HHT）时频分析方法对信号进行处理分析。通过EEMD分解得到的一系列IMF分量再通过HHT变换得到信号局部能量和瞬时频率［14-15］，由此可得出能量-频率-时间的关系，找到损伤信号到达时间，原理如下：

由于Lamb波无损检测中采集到的响应信号是非平稳信号［16-17］，频率值不是固定不变的，因此需要研究信号的瞬时频率［18］。瞬时频率为信号在某一时间点信号相位的变化速度。通常，对于信号[xt]的希尔伯特变换[Hxt]为

[Hxt=yt=limε→0−∞0−εxuπt−udu+0−ε∞xuπt−udu] （10）

假定[−∞∞xt2dtlt;∞]，则公式上可转化为

[Hxt=yt=1πp.v.limε→0−∞∞xut−udu] （11）

其中[p.v.]为柯西主值，[yt]即为[xt]的HT变换。 Braun和Felamann1997年提出，[xt]和[yt]组成了一个共轭复数对，HT变换定义了一种新的信号处理分析方式，这是实数域信号向复数域的延伸，定义新的复数域信号即解析信号为[zt]，则有

[zt=xt+iyt=Atexpiθt] （12）

其中，

[At=x2t+y2t]，[θt=arctanytxt] （13）

由相位即可得出瞬时频率，即

[ωt=dθtdt] （14）

这些定义构成了时频表示的基础，原始信号经过EEMD处理后，得到的是一组瞬时频率有意义的本征模式函数分量，也就是IMF分量。对每个分量进行 Hilbert变换，就可以求出对应分量的瞬时频率，

[Ijt=Ajtexpiωjtdt] （15）

其中，[Ajt]为第[j]阶本征模式函数[Ijt]的解析信号的幅值。对原始信号的n阶IMF分量分别进行 Hilbert变换后，信号[xt]可以表示为［19］：

[Hω，t=xt=j=1nAjtexpiωjtdt]" （16）

上式实现了在一个三维图中表达幅值与频率和时间这三者之间的关系，展开公式（16）后取实部得到的就是Hilbert幅值谱，简称Hilbert谱，记作：

[Hω，t=xt=Rej=1nAjtexpiωjtdt] （17）

综上，通过对信号进行HHT变换，可以得到每个PZT采集到的响应信号处理后的瞬时幅度图，即瞬时能量谱。当某一时刻t的信号幅值达到最大值时，可认为信号在该时刻到达接收端的PZT，信号能量峰值所对应的时间t即为响应信号的到达时间。记录激励信号的起始时间，将到达时间与激励时刻相减即可得到Lamb波在该路径上的传播时间。

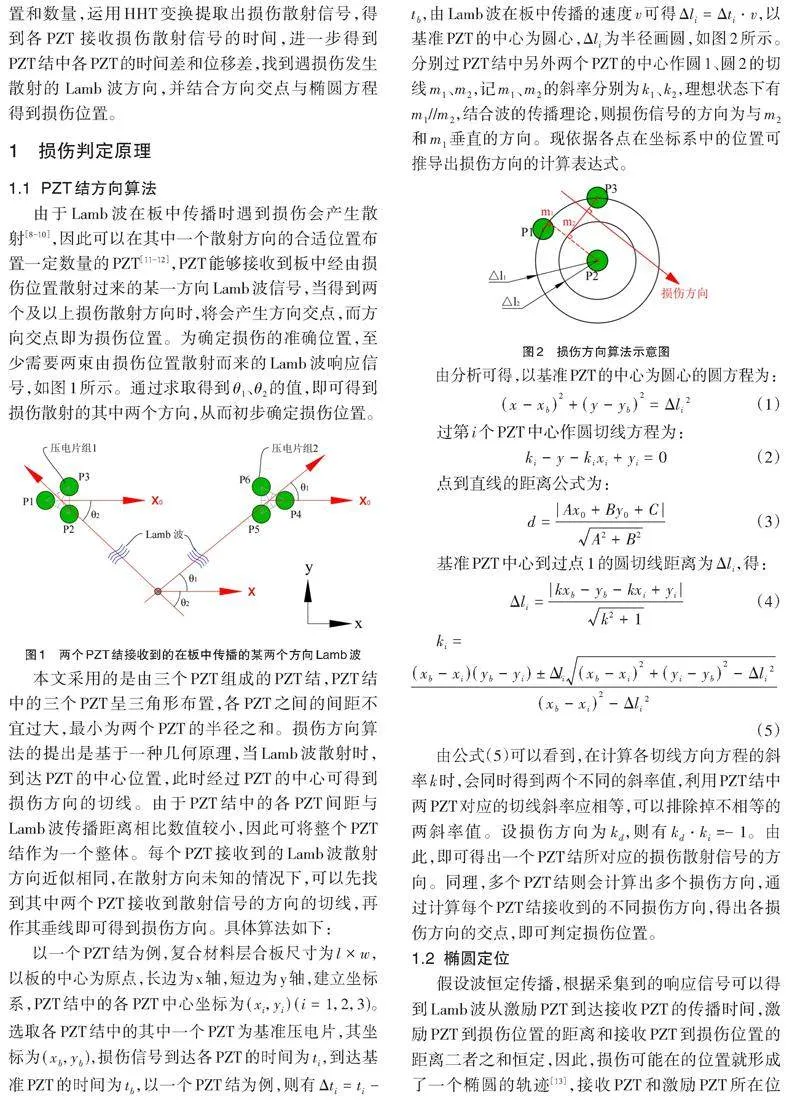
对本次实验中各PZT采集到的健康响应信号与损伤前后差信号分别进行数据分析处理。首先对健康响应信号做HHT分析，得到健康信号的希尔伯特幅值图，并得到健康信号能量峰值点对应的时间[tℎii=1，2，…，7]。再对各PZT接收到的健康响应信号与损伤响应信号作差，得到差信号，对差信号进行HHT分析处理，得到差信号的希尔伯特幅值图及其能量峰值点对应的时间。因实验设置为两个通孔损伤，Lamb波传播时遇损伤边缘总共会有两次反射，各PZT会分别接收到两次散射信号，因此会有两个能量峰值，设损伤散射信号的到达时间为[tdi]，则应有两个到达时间[td1i]、[td2i]。

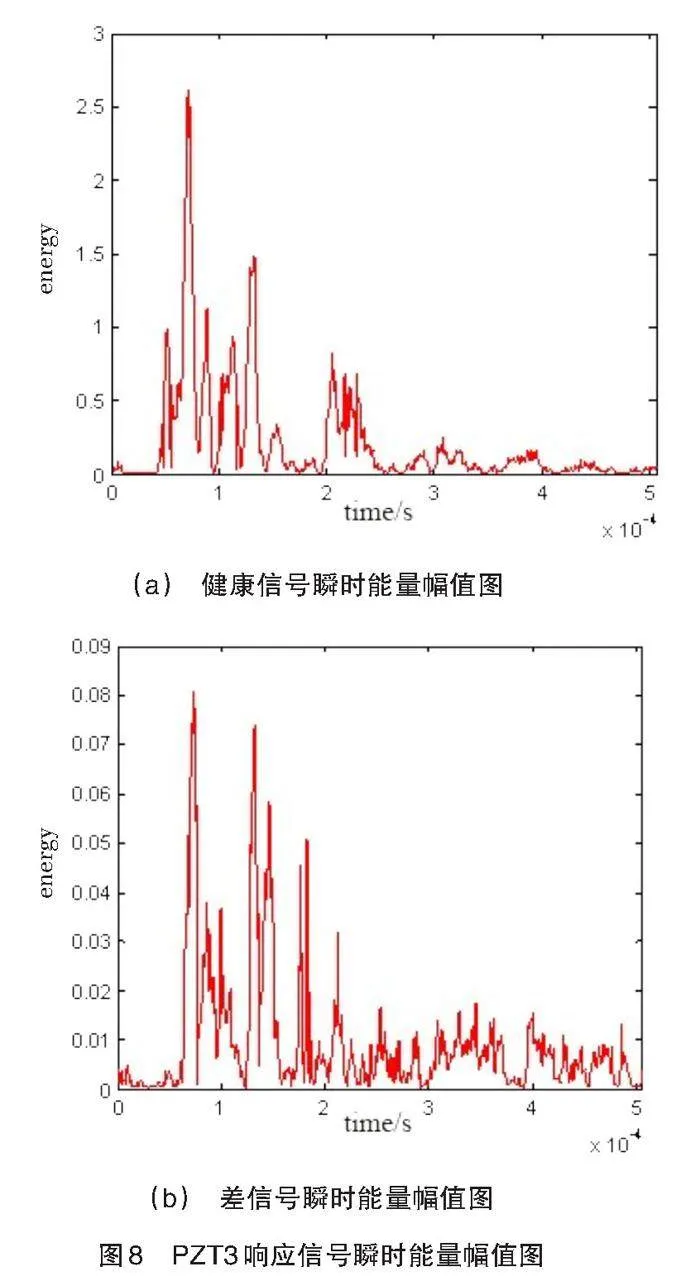
以板中PZT3接收到的响应信号为例，其采集到的健康响应信号和损伤前后差信号如图7所示。

对健康信号和差信号分别进行HHT分析，得到的希尔伯特幅值图如图8所示。

从健康信号中可以看到，PZT接收到的第一个波包，为激励信号直接到达接收PZT的波形。通过对激励信号到达时间的提取，可以计算Lamb波在板中的传播速度。对于差信号的希尔伯特幅值图，从中看出可以得到两个及以上的能量峰值点，根据健康信号的到达时间，可以判断并提取到两个损伤散射信号波包的到达时间。

3 损伤定位

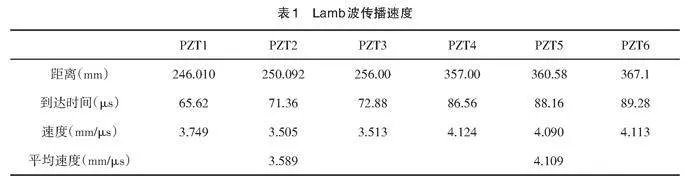
将波形发生器与波形接收器直接相连，得到直连信号，由直连信号可得频率为310 k时设备延时为[t0=9.6×10−6] s。对两个PZT结中的6个接收PZT得到的健康响应信号进行HHT变换，得到的希尔伯特幅值图中第一个能量峰值的到达时间如表1所示。

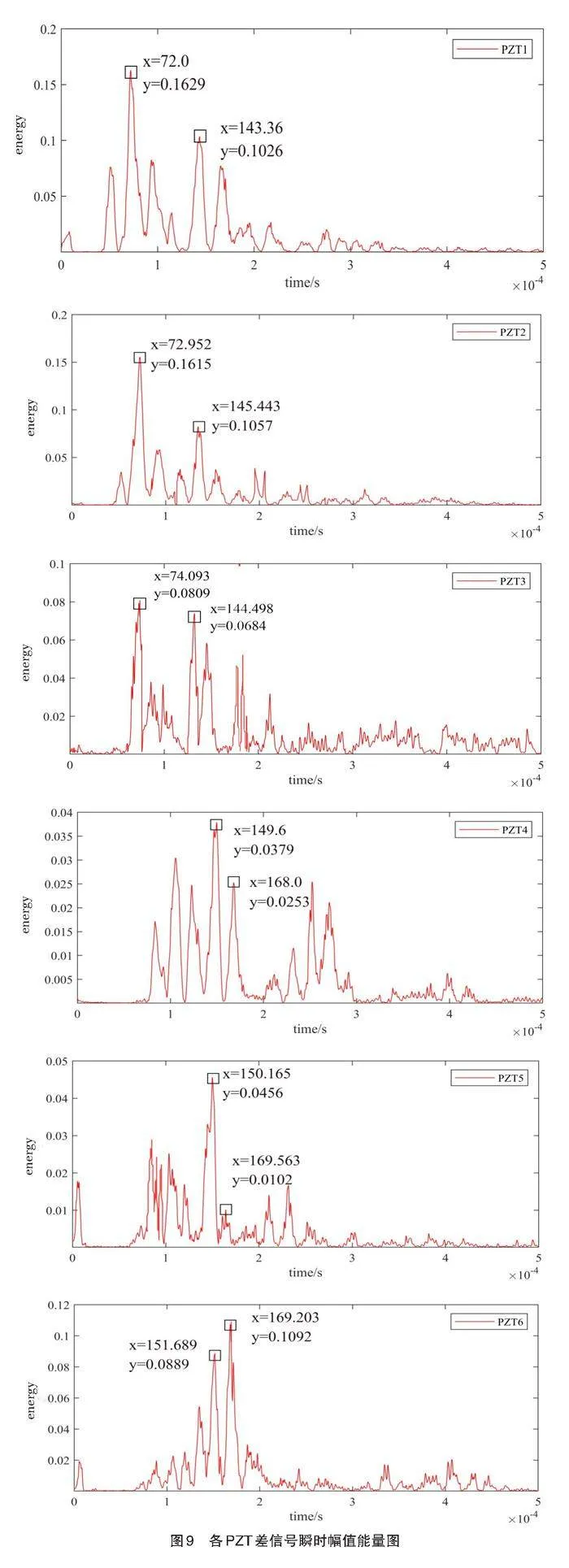
根据激励压电片与接收压电片在板中的位置坐标，可求得PZT0与PZT1、PZT2、PZT3、PZT4、PZT5、PZT6的距离，由速度计算公式[v=s/t]可得Lamb波到达各PZT的传播速度，对各PZT结的各PZT速度求平均值，得到各PZT结的速度。对各PZT的差信号进行HHT变换，得到的瞬时能量幅值图如图9所示。

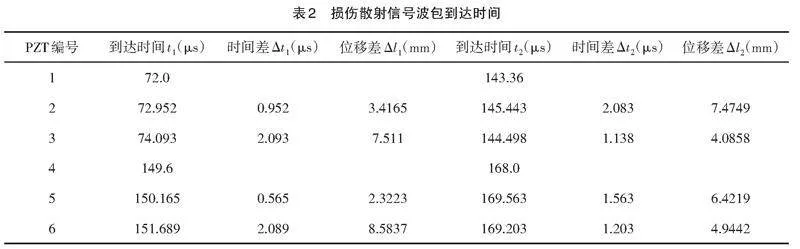
提取差信号的希尔伯特幅值图的能量峰值对应时间，根据峰值对应时间求出各PZT与基准PZT的时间差。依然选取最先接收到信号的PZT为基准PZT。对于PZT结1，选择1号PZT为基准PZT，对于PZT结2，选择4号PZT为基准PZT。由表1中计算所得各PZT结速度，结合差信号中提取出的损伤到达时间，则可得到PZT结中各PZT接收到的损伤散射信号的位移差，各PZT接收到的差信号提取时间如表2所示。

将各PZT坐标代入损伤方向算法计算公式，对于提取各PZT的第一个能量峰值点对应时间，可得PZT结1对应的斜率为：[k11=0.93/0.07]，[k12=0.70/-1.15]；PZT结2对应的斜率为：[k21=1.54/8.14]，[k22=2.36/-1.07]。对应的角度为：[α11=43.00°/3.55°]，[α12=35.38°]/[131.17°]，[α21=56.83°/83.11°]，[α22=67.11°/132.82°]。考虑到实验过程中误差的存在，选取近似相等的角度数据，并取二者平均值，求得两PZT结对应的损伤方向分别为[θ1=140.65°]，[θ2=152.16°]。对于提取第二个峰值能量点对应的时间，可得PZT结1对应的斜率为：[k31=2.90/-0.45]，[k32=1.66/-3.27]，PZT结2对应的斜率为：[k41=0.60/−2.90]，[k42=0.81/-0.34]。对应的角度为：[α31=70.86°/155.68°]，[α32= ][59.47°][/107.08°]，[α41=31.0309°/108.907][°]，[α42=38.91°/161.03°]。同样选取角度近似相等的值，并取平均值，计算可得损伤方向角度为[θ3=165.45][°]，[θ4=124.97°]。

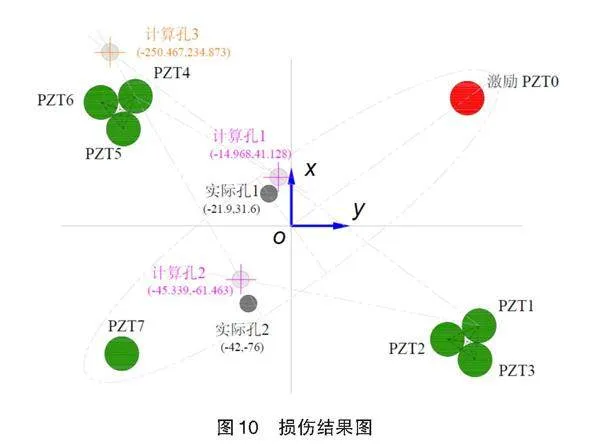
根据得出的各损伤方向，作图得到各方向交点，如图10所示。损伤方向交点有三个，位置分别为图中计算孔1、计算孔2和计算孔3，位置分别为（-14.968，41.128），（-45.339，-61.463）和（-250.467，234.873）。

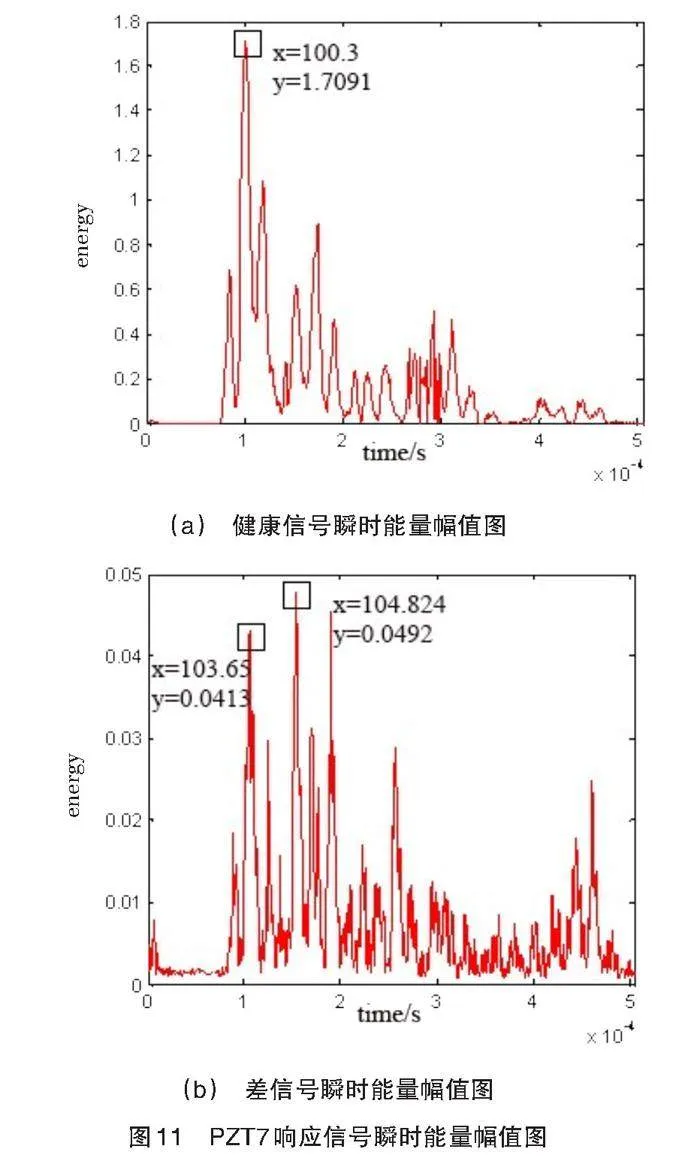
本实验系统中，0号PZT与7号PZT组成一接一收，且两个PZT布置在复合材料板的对角线上，根据坐标可得，二者距离[d0=438.29 mm]，由健康信号能量幅值图得到能量峰值点对应的时间为100.8 [μ]s，由[v=s/t]可得速度为4.348 mm/[μ]s。7号PZT接收到的差信号希尔伯特幅值图如图11所示。

由差信号的希尔伯特幅值图可得两个能量峰值点对应的时间分别为103.65[ μ]s，104.824[ μ]s。将得到的时间与健康信号峰值时间作差，得到[Δt71=2.85 μs，Δt72=4.024 μs]，计算出各自对应的椭圆公式，可得[a1=225.345]，[b1=52.495]，[a2=227.893]，[b2=62.536]。实验设置时，双孔位置距离复合材料板对角线的垂直距离相等，因此，理论上其二者应对应一个椭圆区域。对两个椭圆方程求平均值可得最终椭圆方程为[x2226.622+y257.52=1]。

结合计算得到的椭圆方程，根据损伤方向得出的三个交点只有交点1和2在椭圆附近，因此，排除掉交点3。由此可得损伤位置为（-14.968，41.128），（-45.339，-61.463），两损伤位置与实际损伤位置的距离差分别为12.32 mm和14.92 mm。

4 总 结

本文主要对复合材料板的多损伤问题进行研究，首先对基于Lamb波传播理论的损伤方向算法和椭圆轨迹算法进行了推导；之后搭建复合材料多损伤定位研究实验平台，通过对损伤响应信号进行分析处理，并将损伤方向算法与椭圆定位法相结合，进行损伤位置的判定。得出结论如下：

（1）利用MATLAB 软件编写了基于HHT变换的信号处理方法，在激励频率310 k的条件下，对实验测得的信号数据进行处理，该方法能够提取出损伤散射信号，且对散射信号重构后可以得到损伤散射信号各波包峰值对应的时间；

（2）根据PZT结在板中的位置，并选择1号和4号PZT为基准PZT，利用损伤方向算法得到了各PZT结接收到的经由损伤孔散射的Lamb波方向，确定损伤方向交点位置后，结合椭圆轨迹算法，实现了多损伤位置的判定，且判定位置与实际损伤位置距离分别为12.32 mm和14.92 mm。

结论表明，本文提出的方向算法与椭圆轨迹相结合的损伤定位算法能够对碳纤维增强树脂基复合材料板中的多损伤形式进行定位，且方法简单有效。由于本文仅对损伤判定方法的有效性进行研究，对Lamb波真实传播速度、损伤大小对损伤信号的影响以及实验操作过程中的精度等诸多因素尚未考虑在内，后续将进一步开展深入研究。

参考文献：

［1］张龙，马冀君，李锋伟，等.碳纤维增强树脂基复合材料与金属材料的胶接及混合连接技术研究进展［J］.西安航空学院学报，2022，40（5）：44-57.

［2］何方成，王铮，史丽军，等.航空用纤维增强聚合物基复合材料无损检测技术的应用与展望［J］.无损检测，2018，40（11）：29-32，41.

［3］李娟娟.复合层叠结构兰姆波检测方法研究［D］.太原：中北大学，2020.

［4］韩伟，冯侃，骆英.基于超声Lamb波的双曲线定位损伤成像方法［J］.无损检测，2021，43（4）：46-50.

［5］王高平，李波，徐志勇，等.基于ABAQUS的Lamb波时间反转薄板损伤研究［J］.压电与声光，2021，43（3）：346-351.

［6］HAMCED M S， LI Z， ZHENG K. Damage detection method based on continuous wavelet transfomation of lamb wave signals ［J］. Applied Sciences， 2020，10（23）：8610.

［7］XU J C， ZHU W J， XIANG Y X， et.al. Localization and imaging of micro-cracks using nonlinear lamb waves with imperfect group-velocity matching［J］.Applied Sciences，2021， 11（17）：8069.

［8］杨红娟，杨正岩，杨雷，等.碳纤维复合材料损伤的超声检测与成像方法研究进展［J］.复合材料学报，2023，40（8）：4295-4317.

［9］范朝珠，李志强，刘鹏，等.改进的基于贝叶斯框架和Lamb波的复合材料损伤定位方法［J/OL］.应用力学学报：1-11［2023-10-30］.http：//kns.cnki.net/kcms/detail/61.1112o3.20221123.0852.002.html.

［10］CAMINERO M A，GARCIA-MORENO I， RODRIGUEZ G P，et al.Internal damage evaluation of composite structures using phased array ultrasonic technique： Impact damage assessment in CFRP and 3D printed reinforced composites［J］.Composites Part B：Engineering，2019，165：131-142.

［11］WANDOWSKI T，MALINOWSKI P H，OSTACHOWICZ W M. Circular sensing networks for guided waves basedstructural health monitoring［J］.Mechanical Systemsamp;Signal Processing，2015，66-67：248-267.

［12］KWON D J， KIM J H， PARK S M， et al.Damage sensing， mechanical and interfacial properties of resins suitable for new CFRP rope for elevator applications［J］.Composites Part B：Engineering，2019，157：259-265.

［13］苏晨辉，姜明顺，梁建英，等.强噪声下碳纤维增强树脂复合材料结构Lamb波层析损伤成像方法［J］.复合材料学报，2020，37（4）：886-895.

［14］郭华玲，郑宾，刘艳莉，等.基于EEMD能量熵的激光超声微缺陷信号特征提取[J].测试技术学报，2019，33（5）：393-397，405.

［15］王婷. EMD算法研究及其在信号去噪中的应用［D］.哈尔滨：哈尔滨工程大学，2011.

［16］林宇.基于Lamb波信号时频分析的铝合金结构损伤检测的研究［D］.成都：电子科技大学，2016.

［17］陈栋康康. 碳纤维增强复合材料层合板孔隙缺陷的无损检测方法研究［D］.哈尔滨：哈尔滨工业大学，2022.DOI：10.27061/d.cnki.ghgdu.2022.000244.

［18］LIU Y，HONG X，ZHANG B.A novel velocity anisotropy probability imaging method using ultrasonic guided waves for composite plates［J］.Measurement，2020，166：108087.

［19］孟庆愿.基于希尔伯特黄变换的板状结构健康检测的研究［D］.成都：电子科技大学，2014.

责任编校：刘 燕，田 旭

Research on Multi-Damage Location Method of Composite Materials Based on Lamb Wave

ZHAO Zhujun， FANG Pengya， YAN Lanlan

（Zhengzhou University of Aeronautics， School of Aeroengine，Zhengzhou 450046，China）

Abstract： Aiming at the multiple damage problems of carbon fiber reinforced resin matrix composites for aerospace applications， a damage location method combining damage direction algorithm and elliptical trajectory method was studied. Firstly， according to the propagation characteristics of Lamb wave in the plate， a damage direction algorithm based on PZT junction is proposed. The direction algorithm is used to find several propagation directions of Lamb wave after scattering at the damage location， and the preliminary determination of multiple damage locations is realized through the intersection of the propagation directions. Secondly， the elliptic trajectory algorithm is used to further determine the multiple damage locations. Finally， the method is verified by experiments on carbon fiber reinforced resin matrix composite sheet. The Hilbert yellow transform signal processing technology is used to extract the arrival time of damage scattering signals. The experimental results show that the damage location method can effectively locate multiple damages of composite materials.

Key words： composite material； multi-damage location； direction algorithm

收稿日期：2023-10-30

基金项目：河南省科技攻关项目（222102220047）

作者简介：赵竹君，女，河南漯河人，硕士，助教，研究方向为复合材料超声无损检测。