纤维交叉缠绕复合材料圆柱壳的屈曲分析

摘 要：考虑纤维交叉情况，建立纤维缠绕圆柱壳屈曲有限元分析模型，通过算例验证模型和计算方法的有效性。采用该模型研究了圆柱壳的屈曲载荷随缠绕角、厚径比、长径比等参数的变化情况，并分析计算纤维交叉起伏对圆柱壳屈曲性能的影响。计算结果表明：缠绕复合材料圆柱壳的屈曲临界载荷和屈曲模态与缠绕角、长径比、缠绕层数有很大的关系。在一些特定的情况下，如缠绕角在[10°—30°]范围、长径比较小或者缠绕层数增加时，纤维交叉对屈曲临界载荷有明显的影响。

关键词：纤维交叉；缠绕复合材料；屈曲

中图分类号：TB33" 文献标识码：A" " 文章编号：1007 - 9734 （2024） 05 - 0027 - 09

DOI：10.19327/j.cnki.zuaxb.1007-9734.2024.05.004

0 引 言

纤维缠绕复合材料结构具有比强度大、比刚度高等诸多优点，在航空航天、能源运输、海洋工程等众多领域得到广泛应用。圆柱壳体是这些领域内一种常见的结构形式，而屈曲及稳定性作为圆柱壳体的一项重要性能，一直是各国学者研究的焦点。

Moon等[1]、Hur等[2]利用有限元分析和试验研究了受水下外静压力下缠绕复合材料厚壁圆筒的屈曲和失效情况。Reinoso等[3]设计了一个密封箱实验装置，研究了加筋复合材料圆柱壳在均布压力载荷情况下的屈曲和后屈曲问题。Meyer-Piening等[4]测试了不同组合载荷情况下屈曲载荷。Kho等[5]对轴向压缩载荷作用下的复合材料圆柱壳的屈曲和后屈曲行为进行了理论分析计算。Vaziri等[6]利用板壳理论求解了包含周向和轴向裂纹的圆柱壳的稳定性问题，结果发现，增加0°—25°的铺层可以获得更高的屈曲强度，而增加90°铺层则会使屈曲强度降低。Li和Shen[7]研究了在热环境下轴向受压三维纺织复合材料圆柱壳的后屈曲，Argento和Sco[8]采用摄动法对轴向载荷作用下层合圆柱壳的动态屈曲进行了研究，分析了周向波数和轴向载荷与失稳区域之间的关系。White等[9]利用数值模拟研究了变刚度复合材料圆柱受轴向压缩载荷的后屈曲问题。Lopatin等[10]给出了外部横向压力的复合材料夹层圆柱壳屈曲问题的近似解析解。Peterson等[11]、Smithses等[12]以及Fuchs等[13]修正了屈曲理论，研究了几何缺陷对屈曲性能的影响。闫光等[14]研究了开口尺寸和铺层角度对含矩形开口复合材料圆柱壳屈曲载荷的影响。Bisagni等[15][16]分析了缺陷对圆筒动态屈曲的影响，结果表明其影响程度与铺层顺序相关。Messageret等[17]利用遗传算法优化圆筒叠层方式，Rouhi等[18]提出一种优化模型，对变刚度椭圆复合气瓶优化以获得最大轴向屈曲载荷。还有一些学者研究了缠绕模式对复合材料圆筒屈曲性能的影响。如：Hahn等[19]人观察到屈曲模式对于缠绕模式的依赖性：当缠绕模式类似于预期的屈曲模式时，临界屈曲应力达到最小值。Pai等[20]分析研究了纤维起伏对缠绕复合材料圆筒结构屈曲强度的影响，但其理论分析的结果与实验结果的趋势相反。Hernandez Moreno等[21]研究了缠绕图案对缠绕复合材料结构的力学性能的影响，结果显示，其文中所选择的缠绕图案对结构的屈曲失效载荷没有明显影响。

综上所述，目前对缠绕复合材料圆柱壳屈曲性能的研究，很少涉及纤维束交叉起伏的影响。本研究考虑纤维交叉起伏现象，建立纤维缠绕圆柱壳屈曲有限元分析模型，分析计算圆柱壳的屈曲载荷随缠绕角、缠绕层数、厚径比、长径比等参数的变化情况，研究纤维交叉起伏对圆柱壳屈曲性能的影响。

1 缠绕复合材料缠绕图案

缠绕复合材料结构由一系列菱形特征单元组成[29]，菱形特征单元数目相关的几何参数，以及缠绕复合材料的缠绕图案都可由结构的内径D、纤维束的宽度w以及缠绕角度[q]来确定。

在整个圆周表面缠绕完成缠绕角度为[±q]纤维束，所需要的缠绕循环数目由公式（1）确定。

[Num=πDcosθw] （1）

（1）式中缠绕循环数[ Num ]必须为一个整数，因此在缠绕复合材料制作过程中需要针对不同的内径D调整纤维束的宽度w。假设前一循环和后一循环在芯轴环向间隔数目为[N]，芯轴环向的间隔数目即为缠绕结构在环向方向的菱形特征单元的数目。通常情况下，间隔数目[N]与缠绕循环数[ Num ]没有公因子，因此缠绕复合材料设计时优先选择其中的一个，再计算另外一个。假设每个菱形特征单元所需要的缠绕循环数目为[Num′]，缠绕复合材料缠绕图案可由三个参数确定：芯轴环向间隔数目[N]、缠绕循环数[ Num]和每个菱形特征单元所需要的缠绕循环数目[Num′]，设计缠绕复合材料图案时，三者之间的数值可由（2）式确定。

[Num ′N mod Num=1Num-1] （2）

其中[ mod ]表示求余运算。

图1（a）的缠绕参数：[ Num=10，Num′=10，N=1]；图1（b）的缠绕参数为：[ Num=10，Num′=3，N=3]；图1（c）的缠绕参数为：[ Num=25，Num′=6，N=4]。

纤维交叉起伏区域在笛卡尔坐标系下位置（x，y，z）与缠绕参数（缠绕角度[q]、环向特征单元数目[N]、缠绕结构长度[L]与半径[r]）之间的关系如下：

[ 螺旋向： z=2rarcsinx-r2+y2/2rtanθ] （3）

[环向： z=m2π⋅tanθ/N]

[" " " " " " " " " " " m=1，2，3，……，L/2π⋅tanθ/N] （4）

2 屈曲分析模型

有限单元法研究圆柱壳屈曲的分析过程大致如下：先把研究的圆筒结构划分成若干个离散单元，并建立离散单元结点力与结点位移的单元刚度矩阵，再把每个单元刚度矩阵集合起来形成整个结构的刚度矩阵，最后通过最小势能原理计算临界荷载。

每个离散单元的位移由公式（5）确定：

[u=i=1nNiuiv=i=1nNiviw=i=1nNiwiθx=i=1nNiθxiθy=i=1nNiθyiθz=i=1nNiθzi] （5）

其中n为单元节点的数目，N为单元形函数。定义矩阵q为：

{qi}={ui" " vi" "wi" θxi" θyi" θzi} （6）

结构在外载荷下的总势能由公式（7）确定：

[Π=12ΩσTεdΩ-λqTf]" （7）

其中式（7）第一项为圆柱壳结构的弹性势能，第二项为外载荷产生的势能。[l]为载荷参数，[f]为载荷矢量，应力矩阵[σ]由公式（8）确定：

[σ=Cε] （8）

公式（8）中：[ε]为应变矩阵，[C]为材料的刚度矩阵，需要注意的是，在缠绕复合材料圆柱筒内由于纤维交叉导致纤维交叉区域的刚度与层合区域的刚度不同，利用文献[22]所建立的模型计算纤维交叉起伏区域的刚度。

对结构总势能求变分得到：

[k0-λkpx=0] （9）

[K0]为整体刚度，[Kρ]为初始应力刚度，其具体表达式如下：

[K0=j=1mK0j Kρ=j=1mKρj] （10）

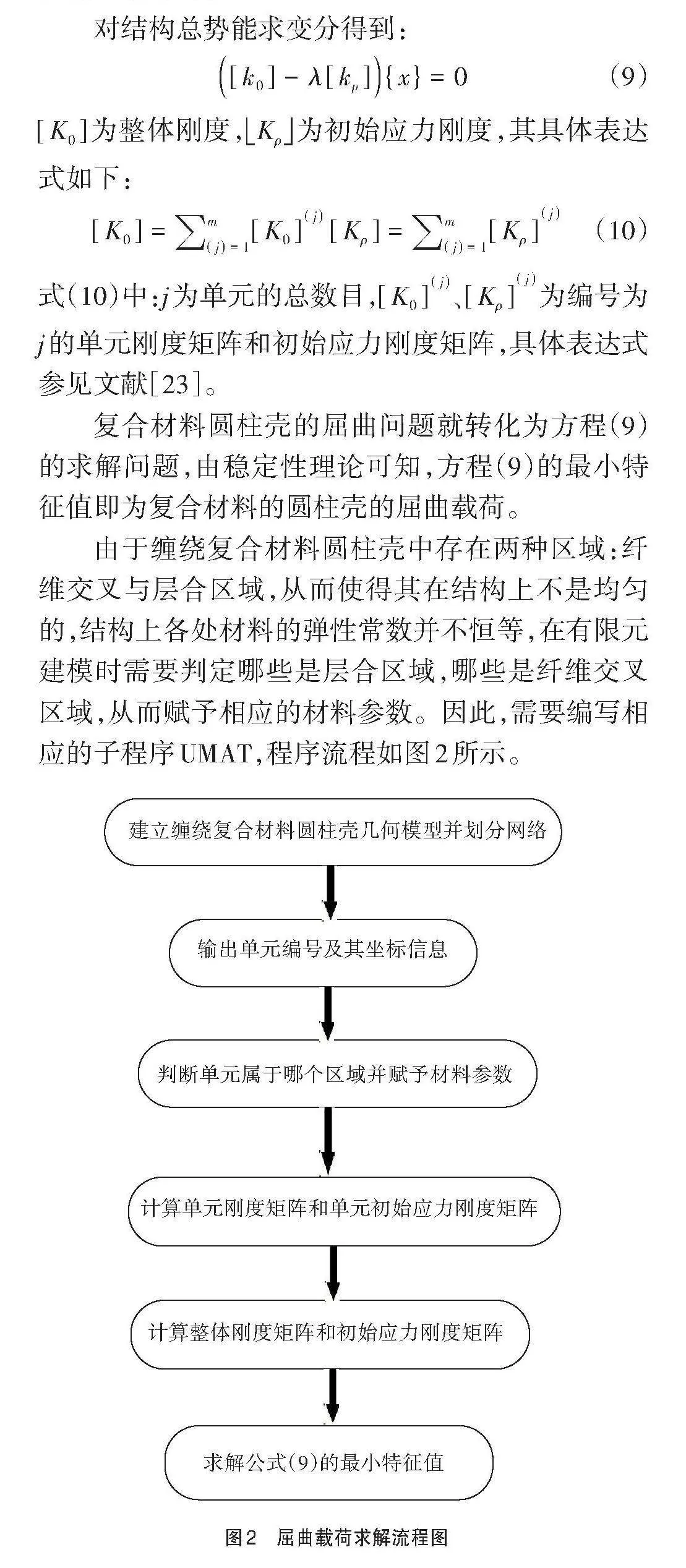
式（10）中：j为单元的总数目，[K0j、Kρj]为编号为j的单元刚度矩阵和初始应力刚度矩阵，具体表达式参见文献[23]。

复合材料圆柱壳的屈曲问题就转化为方程（9）的求解问题，由稳定性理论可知，方程（9）的最小特征值即为复合材料的圆柱壳的屈曲载荷。

由于缠绕复合材料圆柱壳中存在两种区域：纤维交叉与层合区域，从而使得其在结构上不是均匀的，结构上各处材料的弹性常数并不恒等，在有限元建模时需要判定哪些是层合区域，哪些是纤维交叉区域，从而赋予相应的材料参数。因此，需要编写相应的子程序UMAT，程序流程如图2所示。

3 结果与讨论

图3为缠绕复合材料几何模型，黄色部分表示纤维交叉起伏区域，浅绿色部分表示层合区域，Ni表示考虑纤维交叉时环向菱形数目为i个。可以看到，随着环向菱形数目的增加，纤维交叉起伏区域所占的比例也随着增大。

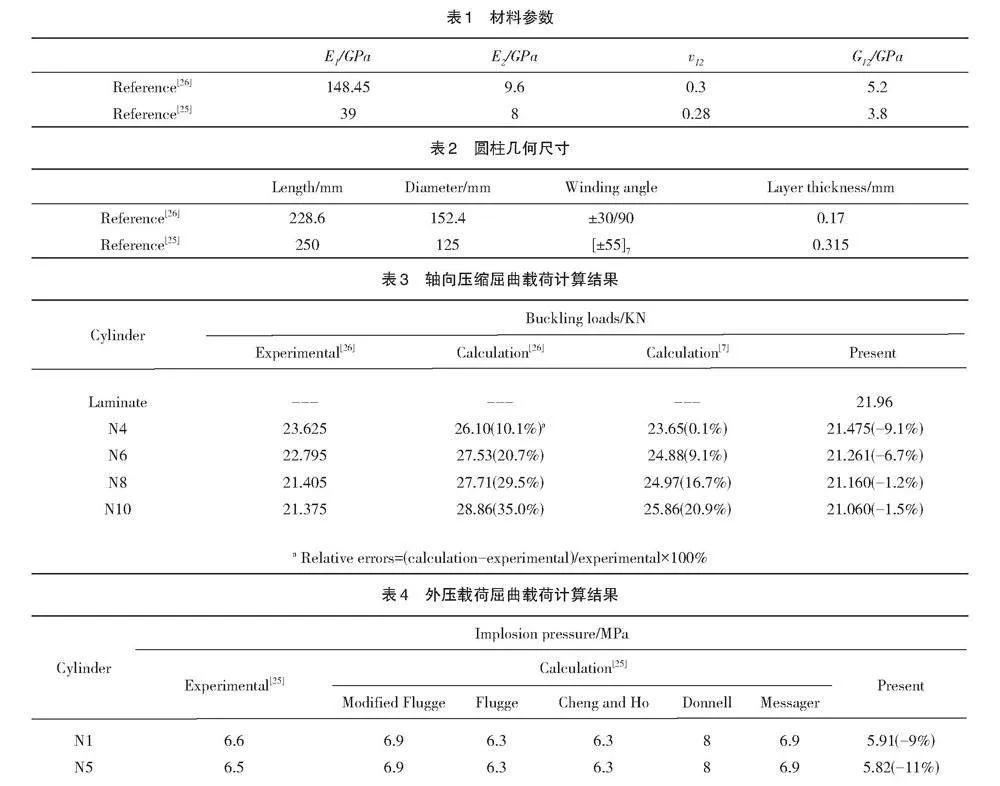
采用文献[7][19][20]中给出的材料参数以及结构几何参数，来分析计算在受轴向压缩以及外压载荷下的屈曲载荷。材料参数以及圆柱壳的几何参数如表1、表2所示，表3、表4给出本文的计算结果，同时与相关文献的结果进行了对比。文献[19]分析计算时采用了5种模型：Modified Flugge模型、Flugge模型、Cheng and Ho模型、Donnell模型和Messager模型，在表4中分别给出相关计算结果。

通过与相关文献的结果进行对比，可以看出本文预测的屈曲载荷与文献[20]的实验结果较为相近，误差在10%以内，并且屈曲载荷随着环向菱形的数目增加略有减小，这与文献[20]的实验结果变化趋势也相同。

3.1 轴向载荷下屈曲情况

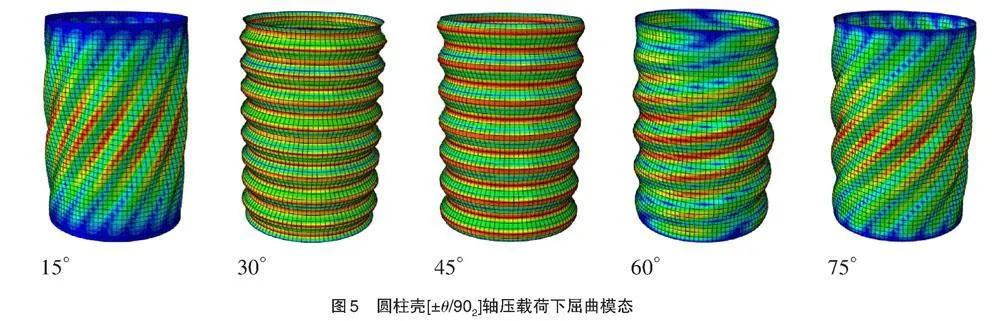
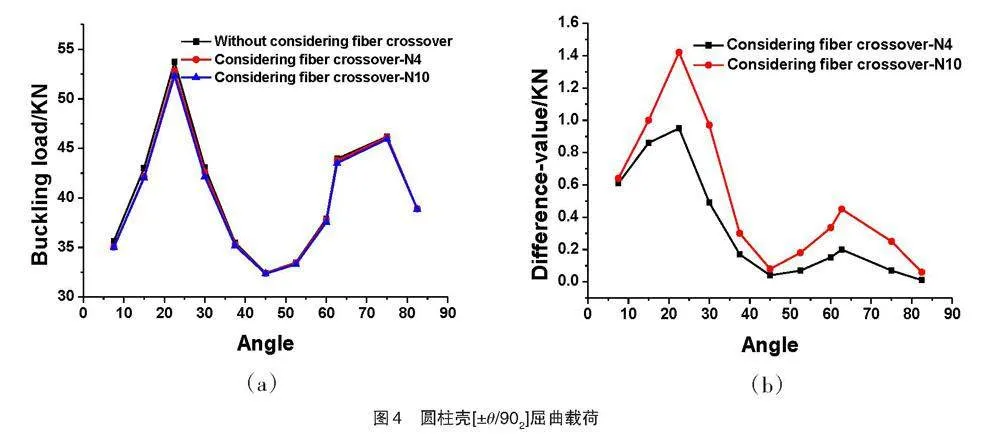
图4（a）给出圆柱壳[±θ/902]轴向屈曲载荷与缠绕角θ关系，图中N4、N10表示考虑纤维交叉时环向菱形数目，由图4（a）可以看出缠绕角度分别在[10°—45°][45°—80°]范围内，屈曲临界载荷先随着缠绕角的增大而增大，然后随着缠绕角的增大而减小。缠绕角度在[10°—30°]区间内屈曲载荷较大，缠绕角度为45°时轴向屈曲载荷较小。图4（b）给出考虑纤维交叉情况下环向菱形数目分别为N4、N10时屈曲载荷与未考虑纤维交叉起伏时的屈曲载荷的差值，可以看到，当环向菱形数目增多时，屈曲载荷有所下降，特别是缠绕角度在[10°—40°]范围，纤维交叉起伏对屈曲载荷的影响尤为明显。图5为圆柱壳[±θ/902]轴压载荷下屈曲模态。可以看到屈曲模态随着缠绕角θ变化而变化，15°、60°和75°的屈曲模态为螺旋向波形，15°与75°的螺旋角较大，60°的螺旋角较小；30°、45°的屈曲模态为轴向波形，30°的波形数目较多。

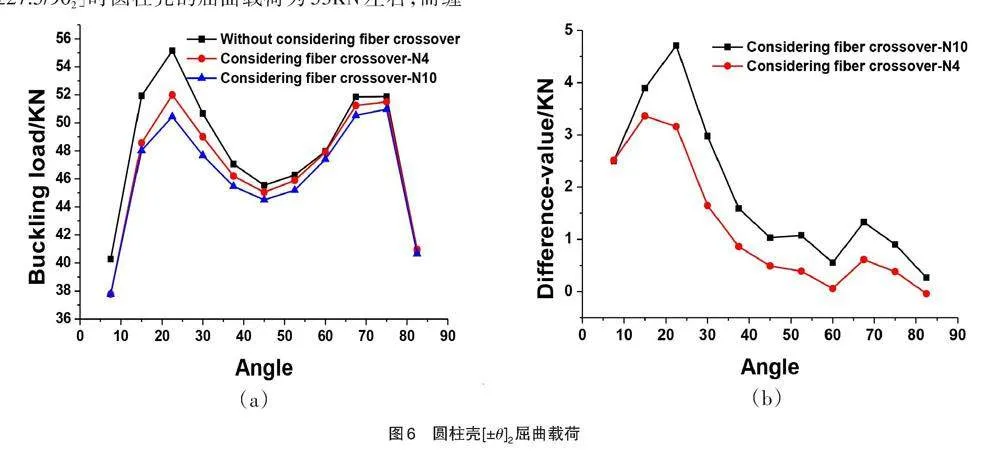
图6（a）为圆柱壳[±θ]2轴向屈曲载荷与缠绕角θ关系。与图4（a）的结果相比，把90°铺层替换为±θ铺层时，结构的屈曲载荷有明显的增大，如缠绕角为[±27.5/902]时圆柱壳的屈曲载荷为53KN左右，而缠绕角为[±27.5]2时其屈曲载荷增至55KN；缠绕角为[±45/902]时圆柱壳屈曲载荷为32.5KN左右，缠绕角度[±45]2时其屈曲载荷增至45KN。

lt;E：＼2023田田＼10--＼郑州航空工业管理学院学报202405＼Image＼ADBF53EA-B476-42e9-A5BA-9B3B6C273305.bmpgt;[（a）]lt;E：＼2023田田＼10--＼郑州航空工业管理学院学报202405＼Image＼0A2C8C0C-C0DA-421d-A7DE-CDDAA93E1E57.bmpgt;[（b）]

图6 圆柱壳[±θ]2屈曲载荷

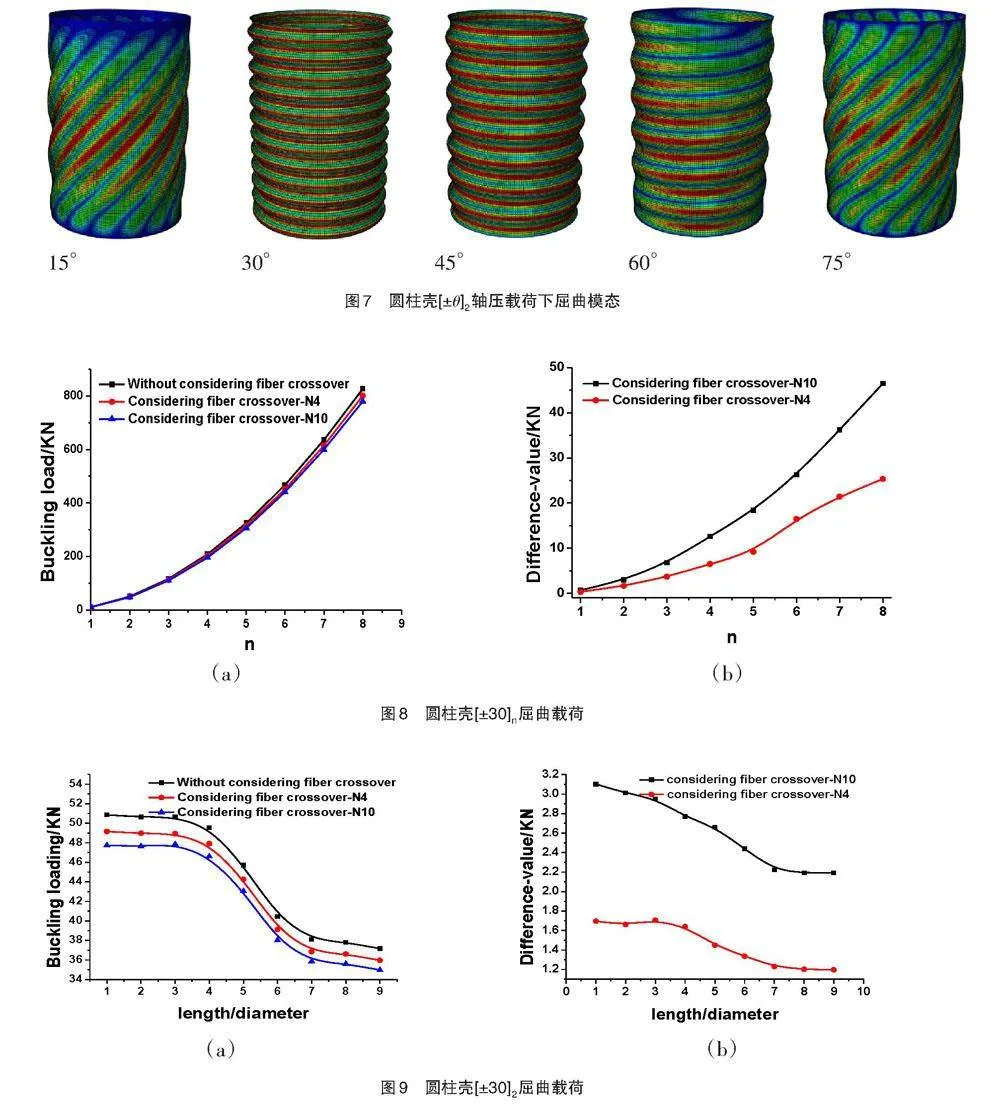
图7（b）给出考虑纤维交叉情况下环向菱形数目分别为N4、N10的屈曲载荷与未考虑纤维交叉起伏情况的屈曲载荷的差值，可以看到，当环向菱形数目增多时，屈曲载荷有所下降。对比图4（b）、图6（b），可以发现，当缠绕层由[±θ/902]改变为[±θ]2时，纤维交叉起伏对轴向屈曲载荷的影响更为明显。图7为圆柱壳[±θ]2的轴压载荷下屈曲模态。可以看到，屈曲模态随着缠绕角θ变化而变化，15°、60°和75°的屈曲模态为螺旋向波形，15°与75°的螺旋角较大，60°的螺旋角较小，30°和45°的屈曲模态为轴向波形，30°的轴向波形数目比45°的数目多。

图8（a）为圆柱壳[±30]n轴向屈曲载荷与铺层层数n关系，可以看出轴向屈曲载荷随着铺层层数n的增加而增加。图8（b）给出考虑纤维交叉情况下环向菱形数目分别为N4、N10时屈曲载荷与未考虑纤维交叉起伏情况时屈曲载荷的差值，可以看到，铺层层数n越多，纤维交叉起伏对屈曲载荷的影响越大。

图9（a）为圆柱壳[±30]2屈曲载荷与长径比之间的关系。可以看出，长径比小于3时，屈曲载荷较大；长径比大于3以后，屈曲载荷急剧下降；长径比大于7以后，屈曲载荷变得很小。图9（b）给出环向菱形数目分别为N4、N10时屈曲载荷与未考虑纤维交叉起伏情况时屈曲载荷的差值，可以看出，长径比越小，纤维交叉起伏对屈曲载荷影响越大。

3.2 外压载荷下屈曲情况

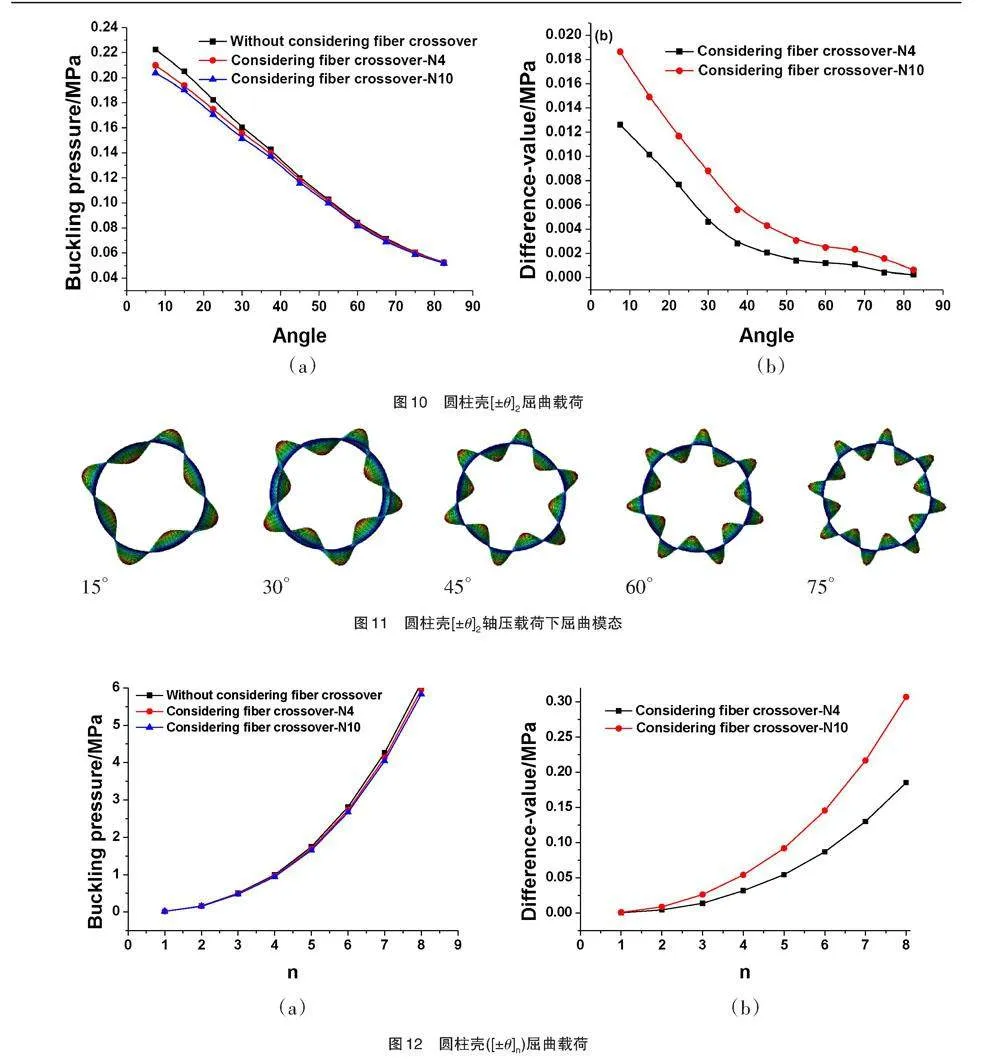
图10（a）为圆柱壳[±θ]2受外压载荷情况下，屈曲载荷与缠绕角的关系。可以看出，当缠绕角度增大时，屈曲载荷减小。图10（b）给出考虑纤维交叉情况下环向菱形数目分别为N4、N10时屈曲载荷与未考虑纤维交叉起伏情况时屈曲载荷的差值，可以看出，对小缠绕角度情况，纤维交叉起伏对屈曲载荷有明显影响。

图11为圆柱壳[±θ]2外压载荷下屈曲模态。可以看出，在外压载荷的情况下，所有的屈曲模态均为环向波形，其波形的数目随着缠绕角的增大而增加。

图12（a）为圆柱壳[±θ]n受外压载荷情况下，屈曲载荷与铺层层数n的关系。可以看出，屈曲载荷随着铺层数增大而增大。图12（b）为考虑纤维交叉情况下环向菱形数目分别为N4、N10时屈曲载荷与未考虑纤维交叉起伏情况时屈曲载荷的差值，可以看出，铺层数n越大，纤维交叉起伏对屈曲载荷的影响越大。

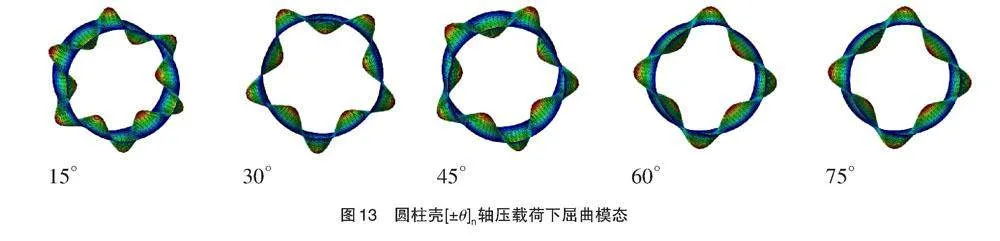
图13为圆柱壳[±θ]n外压载荷下屈曲模态。可以看出，在外压的情况下，环向波形的数目随着缠绕层数的增加而减小，只有1对缠绕层圆柱壳的波形数目为6，有2对或者3对缠绕层时，波形数目均为5，当缠绕层增加到4对或者5对缠绕层时，环向波形数目降低到4。对比图12、13，可以发现，波形数目越少，屈曲载荷越大。

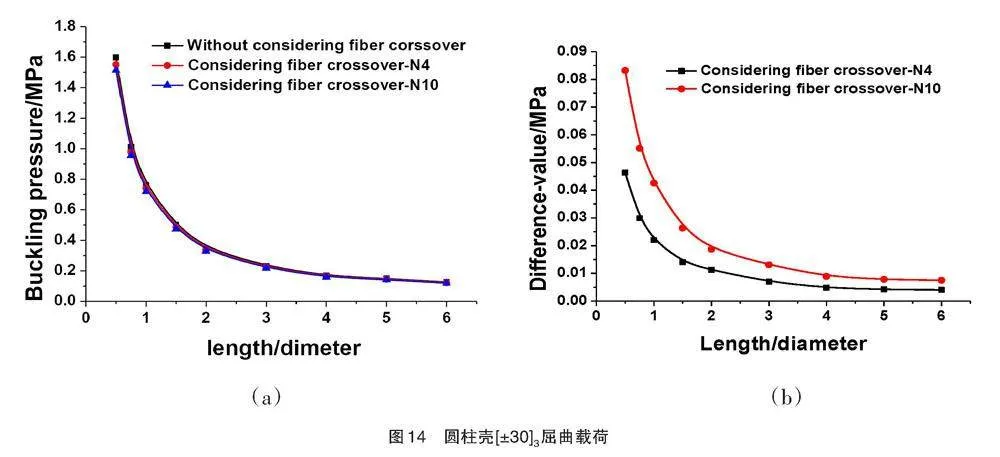
图14（a）为圆柱壳[±θ]3受外压载荷情况下，屈曲载荷与长径比的关系。可以看出，当长径比小于3时，屈曲载荷随着长径比的增大而急剧下降。图14（b）给出考虑纤维交叉情况下环向菱形数目分别为N4、N10时屈曲载荷与未考虑纤维交叉起伏情况时屈曲载荷的差值，可以看出，长径比越小，纤维交叉起伏对屈曲载荷的影响越大。

4 结 论

本研究考虑纤维交叉起伏，建立纤维缠绕圆柱壳屈曲有限元分析模型，通过圆柱壳环向菱形特征单元数目的改变，分析计算纤维交叉起伏对圆柱壳屈曲性能的影响，并且研究了圆柱壳的屈曲载荷随缠绕角、厚径比、长径比等参数的变化情况。通过算例计算结果表明：轴向载荷下，随着环向菱形数目的增加，纤维交叉起伏区域所占比例增加，屈曲载荷有所下降，特别是缠绕角度在[10°—30°]范围，纤维交叉起伏对屈曲载荷的影响尤为明显；外压载荷下，屈曲载荷随着环向菱形数目增加而下降，对于小缠绕角度的情况，纤维交叉起伏对屈曲载荷的影响更为明显；轴向载荷下，圆柱壳的屈曲模态为螺旋向波形和轴向波形，随着缠绕角度变化，螺旋向波形的螺旋角以及轴向波形的数目有所改变；外压载荷下，圆柱壳的屈曲模态为环向波形，其波形数目随缠绕角度变化；圆柱壳的长径比对屈曲载荷有明显的影响，长径比小于3时，屈曲载荷急剧下降。长径比越小，纤维交叉起伏对屈曲载荷的影响越大；外压载荷下，圆柱壳的屈曲载荷随着缠绕层数的增加而增大。缠绕层数越多，纤维交叉起伏对屈曲载荷的影响越大。

参考文献：

［1］MOON C J，KIM I H，CHOI B H，et al.Buckling of filament wound composite cylinders subjected to hydrostatic pressure for underwater vehicle applications[J].Composite Structures，2010，92（9）：2241-2251.

［2］HUR S H，SON H J，KWEON J H，et al.Postbuckling of composite cylinders under external hydrostatic pressure[J].Composite Structures，2008，86（1）：114-124.

［3］REINOSO J，BLÁZQUEZ A，PARÍS F，et al.Postbuckling behaviour of a pressurized stiffened composite panel：part I：experimental study[J].Composite Structures，2012，94（5）：1533-1543.

［4］MEYER-PIENING H R，FARSHAD M，GEIER B，et al.Buckling loads of CFRP composite cylinders under combined axial and torsion loading：experiments and computations[J].Composite Structures，2001，53（4）：427-435.

［5］KHOT N S，VENKAYYA V B，BERKE L，et al.Buckling and postbuckling behavior of initially imperfect orthotropic cylindrical shells under axial compression and internal pressure instability of continuous systems[M].Berlin Heidelberg：Spring Press，1971.

［6］VAZIRI A.On the buckling of cracked composite cylindrical shells under axial compression[J].Composite Structures，2007，80（1）：152-158.

［7］LI Z M，SHEN H S.Postbuckling analysis of three-dimensional textile composite cylindrical shells under axial compression in thermal environments[J].Composites Science amp; Technology，2008，68（3-4）：872-879.

［8］ARGENTO A，SCOTT R A.Dynamic instability of layered anisotropic circular cylindrical shells，Part I：theoretical development[J].Journal of Sound and Vibration，1993（162）：311-322.

［9］WHITE S C，WEAVER P M，WU K C.Post-buckling analyses of variable-stiffness composite cylinders in axial compression[J].Composite Structures，2015，123（10）：190-203.

［10］LOPATIN A V，MOROZOV E V.Buckling of the composite sandwich cylindrical shell with clamped ends under uniform external pressure[J].Composite Structures，2015，122（122）：209-216.

［11］PETERSON J P，SEIDE P，WEINGARTEN V I，et al.Buckling of thin-walled circular cylinders[R].NASA Technical Reports，1968.

［12］SIMITSES G J.Buckling of moderately thick laminated cylindrical shells：a review[J].Composites Part B Engineering，1996，27（6）：581-587.

［13］FUCHS J P，HYER M W，STARNES J H.Numerical and experimental investigation of the bending response of thin-walled composite cylinders[R].Virginia Tech，1993.

［14］闫光，韩小进，阎楚良，等.复合材料圆柱壳轴压屈曲性能分析[J].复合材料学报，2014，31（3）：781-787.

［15］BISAGNI C.Numerical analysis and experimental correlation of composite shell buckling and post-buckling[J].Composites Part B Engineering，2000，31（8）：655-667.

［16］BISAGNI C.Dynamic buckling of fiber composite shells under impulsive axial compression[J].Thin-Walled Structures，2005，43（3）：499-514.

［17］MESSAGER T，PYRZ M，GINESTE B，et al.Optimal laminations of thin underwater composite cylindrical vessels[J].Composite Structures，2002，58（4）：529-537.

［18］ROUHI M，GHAYOOR H，HOA S V，et al.Stiffness tailoring of elliptical composite cylinders for axial buckling performance[J].Composite Structures，2016（150）：115-123.

［19］HAHN H T，JENSEN D W，CLAUS S J，et al.Structural design criteria for filament-wound composite shells[R].NASA Technical Reports，1994.

［20］PAI S P，JENSEN D W.Influence of fiber undulations on buckling of thin filament wound cylinders in axial compression[J].Journal of Aerospace Engineering，2001，14（1）：12-20.

［21］HERNÁNDEZ-MORENO H，DOUCHIN B，PAI S P，JENSEN D W.Influence of fiber undulations on buckling of thin filament wound cylinders in axial compression[J].Journal of Aerospace Engineering，2001，14（1）：12-20.

［22］沈创石，韩小平，何欣辉.计及纤维交叉起伏影响的缠绕复合材料刚度分析[J].复合材料学报，2016（1）：174-182.

［23］O C ZIENKIEWICZ.有限元方法.固体力学（第二卷）[M].北京：清华大学出版社，2006.

责任编校：陈 强，裴媛慧

Buckling Analysis of Fiber Crossover Composite Cylindrical Shells

SHEN Chuangshi

（Zhengzhou University of Aeronautics，Zhengzhou 450046，China）

Abstract：This study considers the situation of fiber crossover and establishes a finite element analysis model for the buckling of fiber-wound cylindrical shells.The effectiveness of the model and computational methods is verified through numerical examples.Using this model，the study investigates the variation of buckling loads of cylindrical shells with parameters such as winding angle，thickness-to-diameter ratio，and length-to-diameter ratio，and analyzes the influence of fiber crossover on the buckling performance of the shells.The computational results show that the buckling critical load and mode of fiber-wound composite material cylindrical shells are significantly related to the winding angle，length-to-diameter ratio，and number of windings.Under specific conditions，such as when the winding angle is in the range of [10°-30°]，the length-to-diameter ratio is relatively small，or the number of windings increases，fiber crossover has a noticeable impact on the buckling critical load.

Key words：fiber crossover；fiber-wound composite material；buckling

收稿日期：2023-12-14

作者简介：沈创石，男，甘肃庆阳人，博士，主要研究方向为航空复合材料及其结构力学。