非纯弯作用下I形波板组合梁的弹性屈曲应力
杨淑雁,王天宇,查支祥,王 韬
(1.宁夏大学 土木与水利学院,宁夏 银川 750021; 2.浙大宁波理工学院 土木建筑工程学院,浙江 宁波 315100)
0 引 言
平钢板梁的腹板和翼缘板较薄时容易发生屈曲破坏,具有较大的安全隐患。为提高稳定性能,采用波形钢腹板(简称波板)代替平腹板是一种常见的改进方法,但这种带钢翼缘板的波形钢腹板I形组合梁(简称I形波板梁)的屈曲模式可能由原先的腹板屈曲主导转变为翼缘板屈曲主导,使翼缘板屈曲成为该种梁构件稳定性的主要问题。
由于手风琴效应,波板基本不受弯矩只受剪力[1],且波板的剪应力分布通常可假定为均等分布。基于有限元法的分析结果,应用参数分析法进行拟合研究,可得到精度较高的弹性屈曲强度计算公式。近年来研究方法在不断改进,计算公式的精度也在不断提升[2-6],王韬等[7-8]采用简单模型和全梁模型对波形钢腹板进行了有限元分析和试验研究,结果表明:当屈曲不由整体屈曲主导时,翼缘板提供的约束对波板弹性屈曲强度的影响基本上可以忽略。
纯弯矩的条件下,翼缘板的压应力沿梁长度方向均等分布,这种简单受力状态下的翼缘板弹性屈曲强度研究已取得了一定的成果。近年来,研究人员通过大量纯弯梁试验与数值模拟分析,提出精度越来越高的纯弯条件下翼缘屈曲应力计算式以及极限抗弯强度计算式[9-12]。然而,在大多数情况下,梁所受的弯矩并不是纯弯矩,翼缘板的压应力并不是沿梁长度方向均等分布。例如:钢框架梁和连续梁的弯矩最大值通常出现在梁的端部,并沿跨中方向逐渐递减,端部附近的弯矩与自由端受集中荷载的悬臂梁弯矩相似,受压翼缘板的压应力在梁端处为最大,并沿长度方向逐渐递减。故悬臂梁屈曲的研究意义大于纯弯梁。
K.IKARASHI 等[13]和B.JGER等[14]对非纯弯I形波板梁进行了实验研究和数值模拟,总结出3种破坏模式,分别是翼缘板屈曲主导的受弯破坏、波腹板屈曲主导的受剪破坏以及耦合屈曲主导的弯剪破坏,但无法得出确定这些屈曲模式的关键参数和准确计算式。直至目前,尚未有研究得出非纯弯梁的弹性屈曲强度定量评估方法。
综上,现有的近似公式[9-12]只适用于计算受纯弯矩的I形波板梁的翼缘板弹性屈曲强度,计算方法有待于改进。笔者将以纯弯梁的研究成果为基础,进行扩展研究,首先对现有公式的适用性进行检验,结合大量有限元模型分析结果进行拟合研究,以期提出悬臂梁的弹性屈曲强度近似计算式。
1 有限元模型
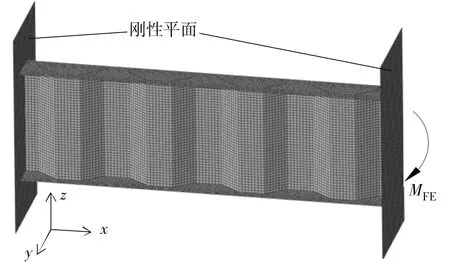
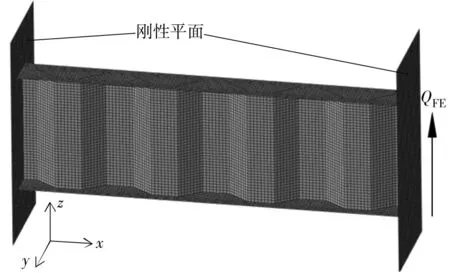
采用有限元法(FEM)进行模拟分析。波板的几何尺寸如图 1,其中板厚t,波峰段(波谷段)长b,波斜宽d,波斜长c,波高hr,翼缘外凸宽cf,翼缘宽bf,翼缘厚度tf。应用ABAQUS软件,建立了两种I形波板梁的模型,如图2、图3;采用壳单元S4R和S3R,腹板网格与翼缘网格采取共节点设置划分。梁的两端都设置了刚性平面,其中左端的刚性平面完全固定,右端的刚性平面限制了y方向的位移以及x、z方向的转动。图2中,弯矩施加于右端刚性平面,为纯弯梁模型;图3中,集中力施加于右端刚性平面,为悬臂梁模型。设置钢材弹性模量E=20 600 MPa,泊松比υ=0.3。
模型弹性屈曲分析结果都采用一阶模态与一阶特征值,纯弯梁的一阶弯矩特征值为MFE,受压翼缘板弹性屈曲应力σFE0换算如式(1):
(1)
悬臂梁的一阶剪力特征值为QFE,受压翼缘板弹性屈曲应力σFE换算如式(2):
(2)
式中:L为梁的长度,L=m(2b+2d),m为波数;h为梁的高度。
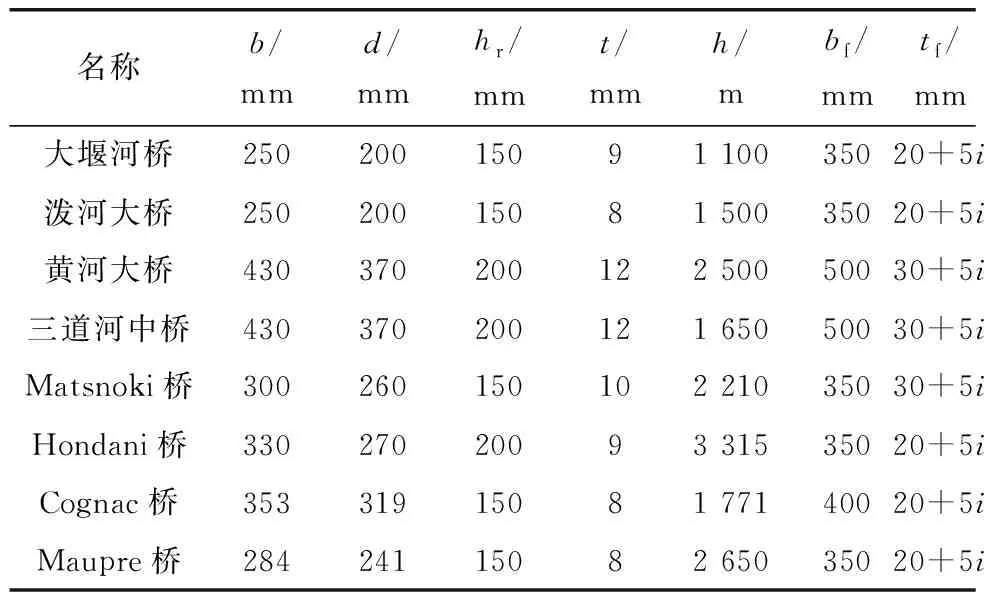
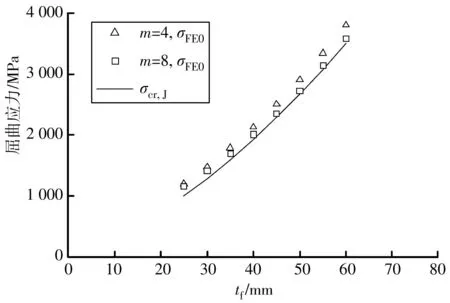
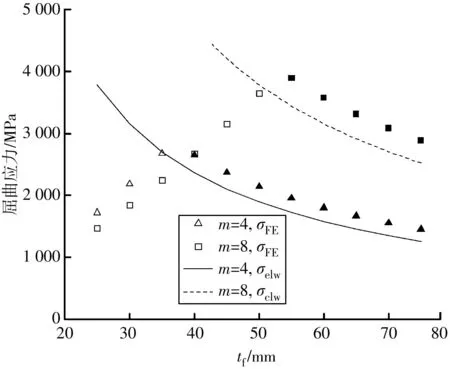
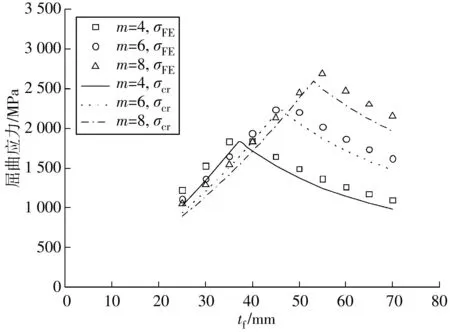
从实际工程角度出发,采用文献 [15]中收集的8个国内外桥梁波板尺寸数据(表 1)进行有限元建模分析。在波板上下添加翼缘板使之成为I形波板梁,并合理设计翼缘板宽度bf在2hr 纯弯矩条件下,梁的屈曲由受压翼缘板屈曲主导。一般情况下tf>2.5t, 文献[12]提出的翼缘板屈曲应力计算公式如式(3)~式(5): (3) (4) (5) 式中:kσ,J为B. Jáger提出的翼缘板屈曲系数;σcr,J为翼缘板屈曲应力。 以表1中大堰河桥的实际参数建立纯弯有限元模型(图2),一组模型中波数m=4,另一组m=8,每组模型翼缘板的厚度tf在25~60 mm之间,其余见表1。采用FEM分析得出MFE后,按式(1)换算得出翼缘板屈曲应力σFE0,tf与σFE0的关系如图4。 表1 模拟对象的几何尺寸[15] 由图4可知:随着tf增大,理论上σFE0会无限增大,但4波与8波得出的σFE0基本上一致,表明在纯弯状态下,翼缘板屈曲应力与波数(或梁长度)基本无关。将式(5)得到的σcr,J曲线在图4中进行比较,发现σcr,J与σFE0基本一致,验证了式(3)~式(5)在纯弯条件下计算翼缘板屈曲强度的适用性。 对于悬臂梁,不仅受压翼缘板可能发生屈曲,受剪的波板也可能发生屈曲。将2.1节中纯弯有限元模型改为悬臂有限元模型(图3),其他参数不变,采用FEM分析得出QFE,并按式(2)换算得出翼缘板屈曲应力σFE,tf与σFE的关系如图5。 由图5可知:4波与8波的I形波板梁的翼缘板屈曲应力相差巨大,表明在悬臂状态下,翼缘板屈曲应力与波数(或梁长度)相关。对此,将式(3)~式(5)计算结果曲线在图5中进行比较可知,在tf=25~75 mm范围内,式(5)得出的σcr,J同样与FEM得出的σFE相差巨大,证明了式(3)~式(5)并不适用于计算悬臂梁翼缘板屈曲强度。 值得注意的是,随着tf增大,σFE先上升后降低。例如图5中,4波的I形波板梁翼缘板屈曲应力σFE在翼缘板厚度tf约为37.5 mm时出现最大值,tf大于37.5 mm时σFE反而减小,但这个现象并不是因为翼缘板的稳定性降低导致的,而是波板屈曲导致的。选取图5中4波I形波板梁tf=25、37.5、55 mm的FEM分析结果,得到3种屈曲模态:翼缘板屈曲主导模态(tf=25 mm)、耦合屈曲模态(tf=37.5 mm)、波板屈曲主导模态(tf=55 mm),如图6。 图6(a)时模态特点为固定端附近约2~3波周边的翼缘板发生屈曲,波板没有发生屈曲,且翼缘板屈曲应力大于式(5)的纯弯状态的翼缘板屈曲应力;图6(b) 时模态特点为翼缘板和腹板同时发生了屈曲,即耦合屈曲;图6(c)时模态特点为屈曲模态由波板屈曲主导。 在翼缘板屈曲主导范围,QFE随着tf的增大而增大;但在波板屈曲主导范围内,翼缘板厚度增减并不影响QFE值,由式(2)可知,tf增大则σFE必定减小,合理解释了图5中σFE先上升后降低的现象。通过以上分析可知,随着翼缘板厚度的增加,I形波板梁的屈曲模态先由翼缘板屈曲主导转变为耦合屈曲,后由耦合屈曲转变为波板屈曲主导;翼缘板的屈曲应力的最大值出现在耦合屈曲的情况。 基于已有的研究成果,笔者将现有公式与FEM结果进行比较,分析公式的适用范围。文献[8]综合考虑波板各屈曲模式下的应力计算模型,得出周边简支波板屈曲应力近似计算如式(6)~式(10),其中式(6)为局部屈曲应力τlel,式(8)为整体屈曲应力τgel,式(9)为合成屈曲应力τiel;式(10)中取3者最小值为波板的屈曲应力,波板的屈曲模态为最小值所对应的屈曲模态。 (6) (7) (8) (9) τel=min{τlel,τgel,τiel} (10) 式中:w为b与c的较大值;w2为b与c的较小值。 式(6)~式(10)的计算结果表明,表1中大部分波板的屈曲模式为合成屈曲(τel=τiel),这与FEM的分析结果吻合。波板发生屈曲时的受压翼缘板压应力换算如式(11): (11) 将图5中的波板屈曲主导的散点改为实心点,翼缘板屈曲主导的散点为空心点,并添加式(11)得出的tf-σelw关系曲线重新绘制悬臂梁的波板屈曲应力如图7。很显然,tf-σelw曲线与实心点较为一致,表明式(11)得出的屈曲应力σelw可以适用于波板屈曲主导的条件。 由于tf-σelw曲线是基于不带翼缘板周边简支的波板屈曲强度计算的近似曲线,所以该曲线略低于带翼缘板的波板屈曲强度,这符合文献[8]的结论,即在大多数情况下,波板的屈曲不由整体屈曲主导(τel≠τgel),该条件下带翼缘板的波板屈曲强度与不带翼缘板周边简支的波板屈曲强度差异不大。另外,由图7可知,随着tf增大,理论上σFE会降低趋近于0,但剪切屈曲强度QFE保持不变。 由表1中的大堰河桥案例分析可知,在翼缘板屈曲主导条件下,悬臂梁的屈曲应力大于纯弯梁。笔者对表1 中的其他案例也进行分析,得出相同的结论。基于表1数据建立的264个悬臂梁模型,基于FEM解析结果表明,有94个模型的屈曲模态为翼缘板屈曲主导,其余的为波板屈曲主导或耦合屈曲。为了评估悬臂梁的翼缘板屈曲应力,选取翼缘屈曲模态下的94个解析结果进行参数化分析,论证屈曲应力与翼缘板尺寸的相关性。FEM的分析结果见图8。 图8中横轴为宽长比X=bf/L,纵轴Y计算如式(12): Y=kFE-kσ,J (12) 图8中X与Y有较好的线性相关性,表明宽长比bf/L越大,悬臂梁的弯矩梯度带来的效果越好,两者的关系可用式(13)近似: Y=2.5X (13) 通过式(4)与式(13)获得悬臂翼缘板屈曲应力σelf的计算公式如式(14)、式(15): (14) (15) 综上,笔者提了出悬臂梁翼缘板屈曲应力计算公式,结合波板屈曲应力计算公式[8],取其小者,可得出如下计算公式: σcr=min{σelw,σelf} (16) 式中:σcr涵盖悬臂状态全部屈曲模态下的应力。 当σelf<σelw时,梁的屈曲由翼缘板屈曲主导;当σelf>σelw时,梁的屈曲由波板屈曲主导;当σelf与σelw接近时,梁的屈曲表现为翼缘板和波板的耦合屈曲。 选取264个悬臂梁有限元模型的分析结果对式(16)的计算误差情况进行分析,如图9,其中横轴为悬臂梁FEM解析结果得出的屈曲应力σFE,纵轴为式(16)的计算结果σcr。 由图9可知,式(16)的计算误差基本可以控制在15%以内,有效证明式(16)对翼缘屈曲强度计算精度较高,能够满足设计要求。 选取表(1)中Hondani桥梁为例,建立波数为m=4、6、8,10种不同厚度翼缘板(选取表1中i=0~9)的悬臂桥梁模型,共3×10=30个,其余尺寸见表1,结果如图10,其中有限元分析得出的计算结果表示为σFE,式(16)计算结果表示为σcr。 图1 波板几何参数Fig. 1 Geometric parameters of CSW 图2 纯弯梁的有限元模型Fig. 2 Finite element model of pure bending girder 图3 悬臂梁的有限元模型Fig. 3 Finite element model of cantilever girder 图4 纯弯梁的翼缘板屈曲应力Fig. 4 Flange buckling stress of pure bending girder 图5 悬臂梁的屈曲应力Fig. 5 Buckling stress of cantilever girder 图6 I形波板悬臂梁屈曲模态Fig. 6 Buckling mode of I-shaped CSW girder 图7 悬臂梁的波板屈曲应力Fig. 7 Web buckling stress of cantilever girder 图8 屈曲应力与翼缘板尺寸相关性分析Fig. 8 Correlation analysis between buckling stress and flange plate size 图9 近似公式的精度验证Fig. 9 Accuracy verification of approximate formulas 图10 屈曲应力的预测结果Fig. 10 10 Prediction results of buckling stress 由图10可知,在tf=25~70 mm范围内,式(16)得出的σcr与FEM得出的σFE结果基本吻合。算例同时证明式(16)适用于不同长度(或波数)条件下的I形波板悬臂梁。 采用有限元法(FEM)研究了I形波板梁的弹性屈曲,分析比较了不同参数下的I形波板梁的屈曲模态,并对现有的计算公式进行了改进,提出了自由端受力悬臂式I形波板梁的弹性屈曲应力计算方法。总结如下: 1)悬臂梁屈曲存在3种模式:翼缘板屈曲、波板屈曲和耦合屈曲,与纯弯梁差异较大。现有的屈曲应力计算公式与笔者的纯弯梁数值模拟结果基本吻合,但与悬臂梁的数值模拟结果不吻合,计算方法需要改进。 2)随着翼缘板厚度的增加,悬臂梁的屈曲模态先由翼缘板屈曲主导转变为耦合屈曲,后由耦合屈曲转变为波板屈曲主导;翼缘板的屈曲应力的最大值出现在耦合屈曲的情况。 3)当屈曲由翼缘板屈曲主导时,悬臂梁的屈曲应力大于纯弯梁。此时,翼缘板的宽长比bf/L是影响翼缘板屈曲的主要因素。以bf/L为参数,对现有的翼缘板屈曲系数和应力进行了修正〔式(14)、式(15)〕并综合考虑波板屈曲应力计算公式〔式(6)~式(11)〕;提出了涵盖全部悬臂梁屈曲模态的屈曲应力计算公式〔式(16)〕。以Hondani桥的参数为算例,验证了笔者的建议公式具有较好的准确性。2 现有近似公式的适用性分析
2.1 纯弯梁的屈曲强度和近似公式
2.2 悬臂梁的屈曲强度和屈曲模态
2.3 波板屈曲强度式适用性分析


3 建议公式
3.1 翼缘板屈曲系数修正公式

3.2 建议公式的精度验证与算例





4 结 论

