长悬臂混凝土箱梁翼缘板受力分析

郭晓雷，　卜建清

(1.石家庄铁道大学交通运输学院，河北 石家庄 050043；2.石家庄铁道大学土木工程学院 河北 石家庄，050043)



长悬臂混凝土箱梁翼缘板受力分析

郭晓雷1，卜建清2

(1.石家庄铁道大学交通运输学院，河北 石家庄 050043；2.石家庄铁道大学土木工程学院 河北 石家庄，050043)

长悬臂混凝土箱梁是一种增加翼缘板宽度的新型截面箱梁，目前我国规范所规定的计算箱梁行车道翼缘板有效分布宽度概念对于长悬臂翼缘板已不再适用。以有限元分析为基础，应用大型有限元ANSYS计算软件，在集中荷载作用下，考虑横向预应力的影响，对长悬臂箱梁翼缘板进行内力分析。结果表明：箱梁端部翼缘板根部负弯矩与箱梁跨中翼缘板根部负弯矩具有明显差异，且横向预应力对翼缘板内弯矩的分布有重要影响。结合数据分析，研究翼缘板内弯矩的分布规律，为其配筋设计提出建议。

长悬臂；翼缘板；半无限板效应；横向预应力

随着交通的发展以及城市空间问题日趋严峻，长悬臂预应力混凝土箱梁由于增加了翼缘板宽度，增加了桥上桥下的空间利用率，提高了桥上桥下通行率，因此得到迅速发展。然而，目前我国《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTJGD062—2004)，对箱梁行车道翼缘板的计算还处于短悬臂阶段，其并不适用于长悬臂行车道板的计算。沙柯(Sawko)[1]通过在集中荷载作用下对长悬臂等厚度截面的行车道翼缘板进行有限元分析，提出了等厚度无限宽矩形行车道翼缘板的弯矩与剪力的表达式。而加拿大贝达巴赫(Baider Bahkt)[2]通过对带边梁变厚度的长悬臂板进行分析归纳，总结了适用于长悬臂截面带边梁的巴赫公式。这两种公式的前提是将翼缘板根部视为嵌固端，然而箱梁是一种空间结构，这两种公式并未考虑箱梁的空间效应。文献[3]通过对悬臂板模型和全箱梁模型的翼缘板根部弯矩进行对比分析，文献[4-6]对长悬臂混凝土箱梁的剪力滞效应进行了分析，表明随着行车道翼缘板宽度的增加，剪力滞效应就越明显；文献[7-8]研究了畸变效应对箱梁翼缘板受力的影响，这些都表明了箱梁翼缘板的空间效应不容忽略。然而，在整个翼缘板长度范围内，行车道翼缘板并不是简单的无限板，在对行车道翼缘板进行分析时还应考虑箱梁端部附近的翼缘板的半无限板效应；同时，随着翼缘板的长度增加，其板内必然设置横向预应力筋。因此，本文在考虑箱梁空间效应的基础上，建立全箱梁空间有限元模型，对箱梁翼缘板内力分布规律进行分析，并考虑横向预应力对其受力规律的影响，总结长悬臂翼缘板受力规律，为长悬臂翼缘板的配筋设计提供参考。

1 模型建立

计算模型为单箱单室长悬臂混凝土简支箱梁模型，桥面宽度14.5 m，高1.8 m，桥梁全长32 m，翼缘板长4.5 m，翼缘板根部0.4 m，翼缘板端部0.2 m，箱梁截面参数如图1所示。

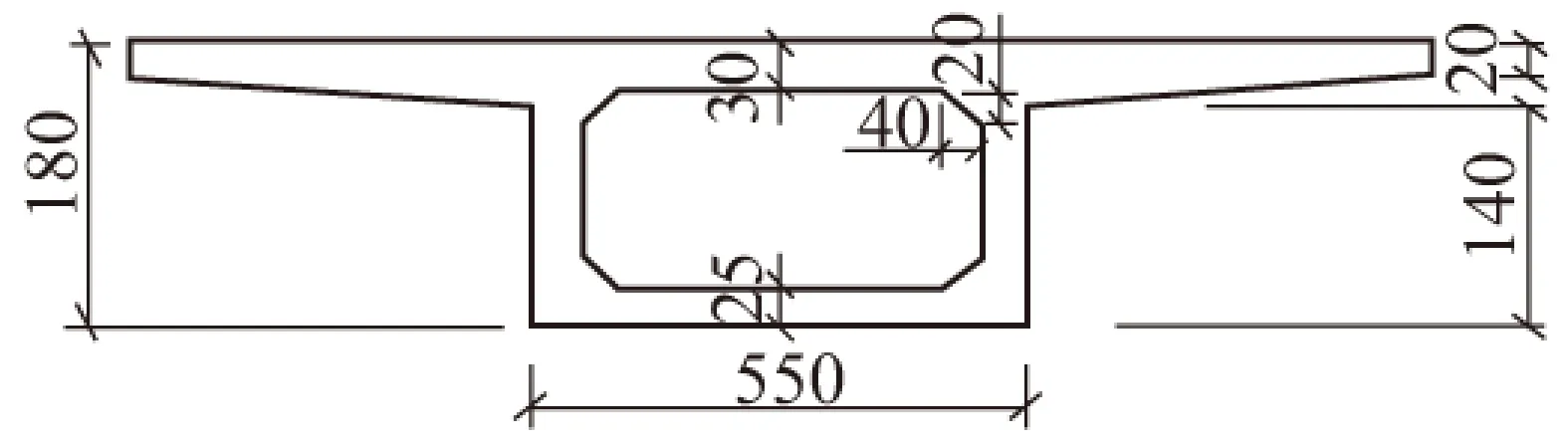
图1　箱梁横截面(单位：cm)

箱梁计算模型采用大型有限元软件ANSYS进行建模分析，模型采用solid65实体单元进行模拟，网格划分采用扫略网格划分方法将模型划分为网格边长为0.5 m的六面体单元，以方便采用面操作法对实体结构进行弯矩提取；同时为了使计算更加精确又保证计算工作时间，在翼缘板处采用网格边长为0.25 m的六面体单元进行了加密。混凝土的弹性模量为E=3.45×104MPa，密度为2.5×103kg/m3，泊松比为0.3。所建模型如图2所示。

图2 全箱梁整体模型

2 长悬臂箱梁翼缘板计算分析

2.1 翼缘板无横向预应力时受力规律的分析

2.1.1翼缘板根部负弯矩的分布

模型在进行计算分析时，采用集中荷载P=100 kN在距箱梁翼缘板边缘1 m处(翼缘板边缘1 m范围内为人行道)，自箱梁端部向跨中方向移动，计算箱梁翼缘板根部的弯矩。规定箱梁上部受拉弯矩为负，下部受拉弯矩为正。计算结果如表1所示。

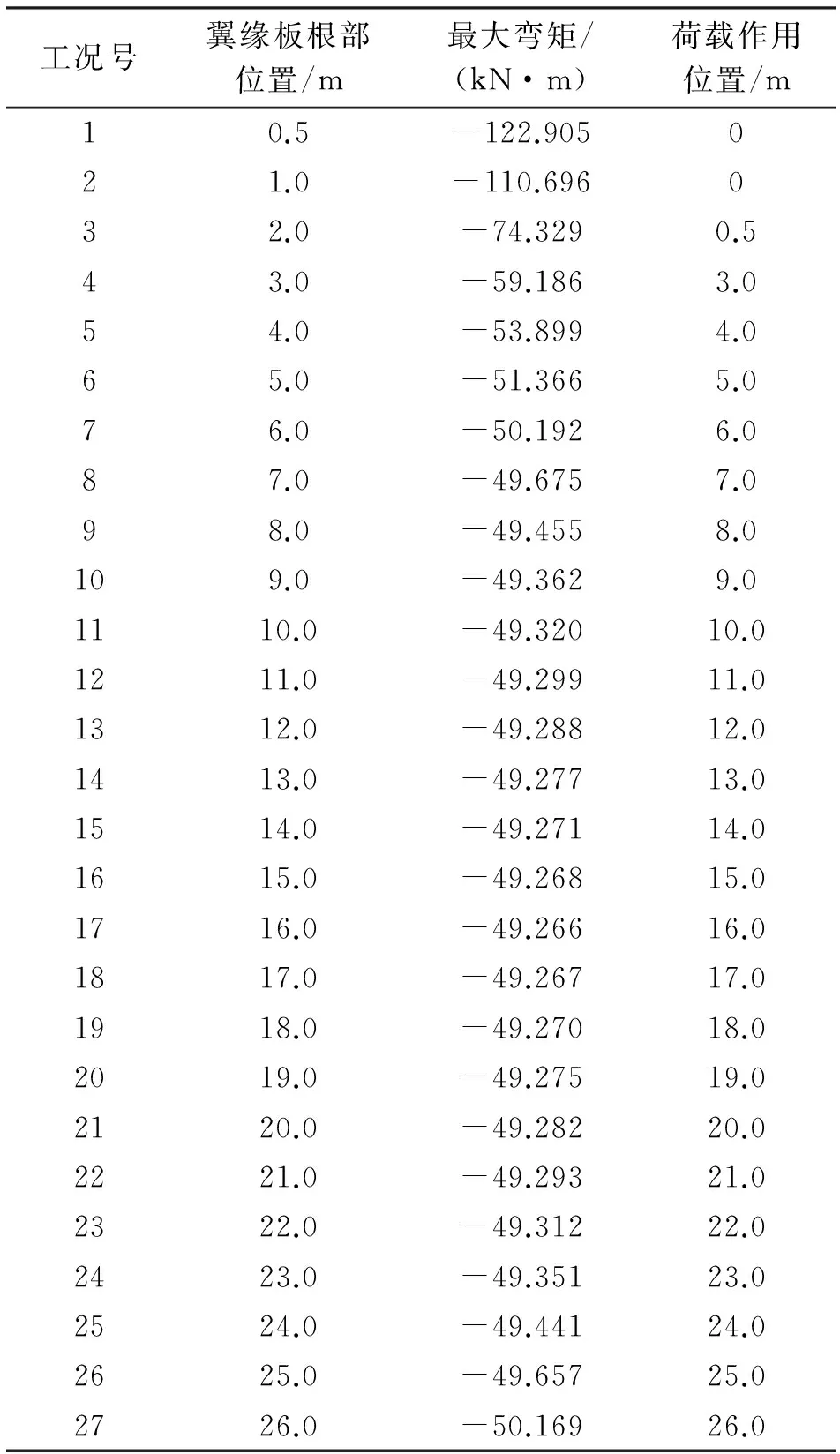
表1 箱梁翼缘板根部弯矩

续表

(1)从表中数据可以看出，箱梁端部的翼缘板根部弯矩与箱梁跨中翼缘板根部弯矩具有明显的不同，且二者相差很大，箱梁端部翼缘板根部弯矩最大为-122.905 kN·m，箱梁跨中范围内翼缘板根部弯矩在-49.266 kN·m上下波动，箱梁端部翼缘板根部弯矩约是箱梁跨中翼缘板根部弯矩的2.5倍。因此，在实际中，对箱梁翼缘板根部弯矩进行配筋时，若按照规范中荷载有效分布宽度公式配筋将造成在整个翼缘板范围内配筋一致，使箱梁端部翼缘板因抗弯钢筋不足而导致翼缘板开裂；因此，建议在实际设计配筋中，箱梁翼缘板配筋应从距箱梁端部1倍翼缘板长度范围内加强配筋。对此，国外规范就有相关规定，日本规范规定，自箱梁翼缘板端部1倍翼缘板跨径范围内，设计时应考虑将翼缘板弯矩增加1倍；加拿大安大略规范中也有相似规定，在距箱梁端部2倍翼缘板范围内翼缘板的配筋设计应考虑加倍。

(2)从箱梁端部翼缘板根部弯矩与箱梁跨中翼缘板根部负弯矩的明显不同可以看出，箱梁翼缘板具有十分明显的半无限板效应。表中数据指出，箱梁跨中翼缘板根部弯矩基本在一个数值上下波动，且波动范围比较小，这表明箱梁跨中翼缘板可以看作无限板；而箱梁端部翼缘板根部弯矩与跨中根部弯矩明显不同且越接近跨中其根部弯矩越趋于一致，说明箱梁端部翼缘板为半无限板，即在实际设计中不能忽略箱梁翼缘板的半无限板效应。

2.1.2翼缘板内最大正弯矩的分布

在箱梁翼缘板内不仅存在着负弯矩，而且还存在着正弯矩，为了分析翼缘板内最大正弯矩分布的位置，现取箱梁端部、1/4跨径处、1/2跨径处翼缘板内部的弯矩进行分析，将集中荷载分别在此三处从翼缘板根部向翼缘板边缘移动，分析荷载在各个位置处最大正弯矩产生的位置。计算结果如图3所示。

(1)荷载在翼缘板内移动时，其正弯矩峰值产生在荷载作用位置处。

图3 翼缘板内最大正弯矩分布图

(2)由图中可以看出，当荷载位于4.25 m与6.25 m之间时，即荷载位于1/3翼缘板长度与7/9翼缘板长之间时，其产生的正弯矩在整个翼缘板内处于最大，在此范围之外正弯矩值迅速减小。

(3)由正弯矩峰值可以看出，箱梁端部与跨中范围内其峰值相差并不是很大，因此，翼缘板端部正弯矩半无限板效应并不是很明显。

2.1.3翼缘板内正弯矩峰值与根部负弯矩的关系

为了分析翼缘板内正弯矩峰值与翼缘板根部负弯矩的关系，现将集中荷载位于产生正弯矩峰值的位置处，翼缘板内弯矩分布如图4所示。

图4 翼缘板内弯矩分布图

在集中荷载100 kN作用下，在整个翼缘板正弯矩峰值接近于20 kN·m，在跨中无限板内，其产生的负弯矩约为-40 kN·m，正弯矩峰值约为根部负弯矩的1/2；而端部半无限板却没有这个关系。因此在进行翼缘板配筋设计时，可考虑翼缘板内正弯矩配筋为在无限板内产生正弯矩峰值荷载作用处时根部产生负弯矩的1/2。

2.2 横向预应力对翼缘板受力规律的影响分析

为了研究在翼缘板内设置横向预应力筋时其对翼缘板内弯矩的分布规律的影响，现将箱梁顶板内设置直径为15.24 mm的钢绞线，将其从距箱梁端部0.5 m处每隔0.5 m设置一束直至箱梁尾部，共设63束，钢束弹性模量为E=1.95×105MPa，质量密度为7 921 kg/m3。设张拉力为25 kN和50 kN，与无横向预应力时进行对比分析，根部负弯矩所得数据如图5所示。

由此可知，随着横向预应力筋张拉力的增大，翼缘板根部负弯矩逐渐减小，说明横向预应力对翼缘板内负弯矩具有明显的卸载作用。

为了得出在箱梁翼缘板范围内，横向预应力对翼缘板正弯矩的影响，所得箱梁端部、1/4跨径、1/2跨径处翼缘板整个范围内正弯矩分布如图6所示。

图5 有无横向预应力翼缘板根部弯矩对比图

(1)由图6可以看出，无论是箱梁端部，还是1/4跨径和1/2跨径处，随着设置的预应力增加，翼缘板内正弯矩明显增加，说明横向预应力筋对正弯矩具有增载作用。因此在对翼缘板配筋设计时，不仅要考虑对负弯矩的卸载作用，还应考虑对正弯矩的增载作用。

(2)图6中数据显示，在2.75～5.75 m之间，也就是在2/3翼缘板范围内横向预应力对翼缘板内正弯矩的增载作用十分明显，超出这个范围其增载作用就不再明显了。

为了明确的比较出横向预应力对翼缘板正弯矩峰值产生位置的影响，现将集中荷载位于产生正弯矩峰值的位置处，翼缘板内弯矩分布如图7所示。

图6 翼缘板内横向位置处弯矩峰值分布图

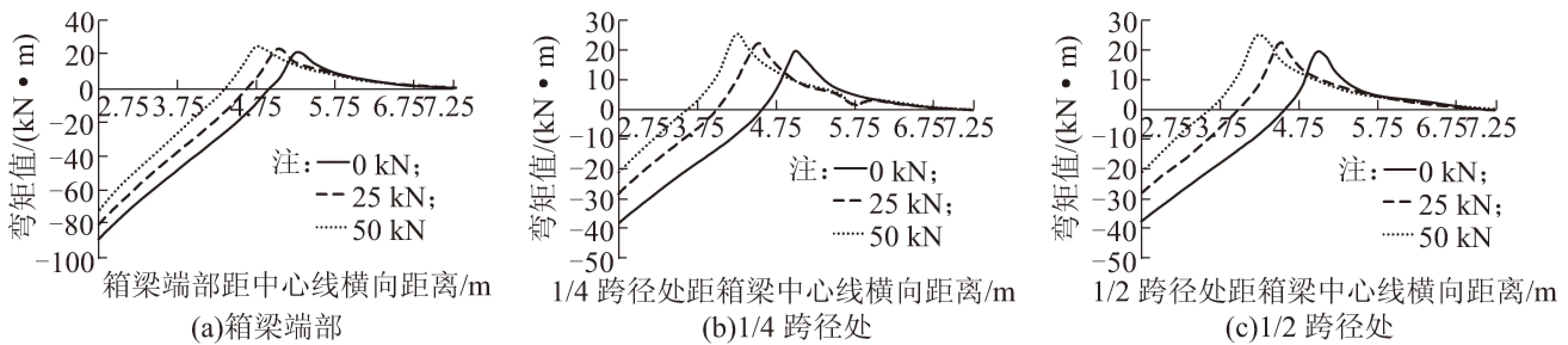
图7 有无横向预应力翼缘板内弯矩分布对比图

由此可以看出，随着横向预应力筋张拉力的增大，翼缘板内正弯矩的峰值逐渐增大且产生正弯矩峰值的位置逐渐向翼缘板根部位置偏移，因此在设置横向预应力的情况下进行正弯矩配筋时，应考虑横向预应力对正弯矩峰值产生位置的影响。

3 结论

(1)长悬臂箱梁端部翼缘板根部负弯矩与箱梁跨中翼缘板根部负弯矩具有很大的差异，表明箱梁端部翼缘板为半无限板，其半无限板效应不容忽略。

(2)不施加横向预应力时，箱梁端部翼缘板根部负弯矩约为箱梁跨中翼缘板根部负弯矩的2.5倍，在对箱梁翼缘板配筋设计时，考虑在距箱梁端部1倍翼缘板跨径范围内钢筋加倍。

(3)在整个箱梁翼缘板内不仅存在负弯矩，而且存在着正弯矩，且在荷载作用处翼缘板内正弯矩达到最大，在不设横向预应力筋时约为翼缘板根部最大负弯矩的1/2。因此对翼缘板进行配筋设计时，不仅需要对负弯矩配筋，还需对正弯矩进行配筋，可考虑翼缘板内正弯矩配筋为在无限板内产生正弯矩峰值时荷载作用处时根部产生负弯矩的1/2。

(4)横向预应力的设置能够有效减少翼缘板内负弯矩，具有明显的卸载效应；同时，横向预应力能够有效的增加翼缘板内的正弯矩，且在翼缘板根部至2/3翼缘板长度内正弯矩的增加比较迅速，具有明显的增载作用。

(5)随着横向预应力的增加，翼缘板内产生正弯矩峰值的位置逐渐向翼缘板根部方向偏移。

[1]SAWKO F,MILLS J H.Design of cantilever slabs for spine beam bridges[J].Developments in Bridge Design and Construction,1971:1-11

[2]BAKHT B.Simplified analysis of edge stiffened cantilever slabs[J].Journal of the Structural Division,1981,107(3):535-550

[3]张 岗，王新敏，贺拴海.混凝土箱梁悬臂板空间数值仿真[J].武汉理工大学学报：交通科学与工程版,2007(3):434-437

[4]郑 振，谷 音.大悬臂变截面箱梁剪力滞效应分析[J].福州大学学报：自然科学版,2001(2):62-65

[5]田 明.宽翼缘箱梁剪滞效应的进一步研究[J].黑龙江交通科技,2011(6):146-147

[6]孔庆凯，童育强，丁继武.宽翼缘预应力混凝土连续箱梁关键受力分析研究[J].公路,2014(6):83-87

[7]项海帆.高等桥梁结构理论[M].北京：人民交通出版社，2001

[8]张文献，庞姝，黄金芬.大翼缘箱梁畸变效应的试验研究[J].东北大学学报：自然科学版,2009(7):1047-1050

On the Stress Analysis of the Flange Plate of a Long-Cantilevered Concrete Box Girder

GUO Xiaolei1，BU Jianqing2

(1.College of Transportation, Shijiazhuang Tiedao University,Shijiazhuang 050043,China；2.College of Civil Engineering,Shijiazhuang Tiedao University,Shijiazhuang 050043,China)

The long-cantilevered concrete box girder is a girder with a new type of cross section.Nowadays,the concept of the effective distribution width of the calculation method for the calculation of the flange plate of a running lane provided by the technical norm is no longer applicable to the calculation of the long-cantilevered flange plate, in which case the large-type finite element calculation software of the ANSYS is applied,upon the basis of the finite element analyses,to the stress analysis of the long-cantilevered flange plate under the concentrated loads, with the influence of the transverse pre-stressing taken into account.The calculated result shows that the negative moment of the root of the flange plate at the ends of the box girder is obviously different from that of the flange plate at the middle of the box girder,and the transverse pre-stressing has a significant impact on the distribution of the bending moment in the flange plate. Combined with data analyses,the distribution law of the bending moment in the flange plate may thus be studied,the result of which can provide useful suggestions for the design of its reinforcement.

long cantilever;flange plate;effect of the semi-infinite plate；transversely pre-stressing

2016-03-07

河北省自然科学基金(E2013210104)，河北省高校百名创新人才支持计划(Ⅱ)，河北省高层次人才资助项目(A201400213)

郭晓雷(1992—)，男，硕士研究生，研究方向为交通运输工程。antcavalier@163.com

10.13219/j.gjgyat.2016.05.012

U448.213

A

1672-3953(2016)05-0040-05