轴向循环载荷下扁钢加筋板极限强度研究

崔虎威,方文武,丁启印

(1. 重庆交通大学 航运与船舶工程学院,重庆 400074;2. 重庆高新开发建设投资集团有限公司,重庆 401329;3. 招商局重庆交通科研设计院,重庆 400041;4. 内河航运技术湖北省重点实验室,湖北 武汉 430063)

0 引 言

船体梁的总纵强度是船舶结构设计的关键指标,也是船舶安全航行的基本保障。船体加筋板作为船体梁的基本组成单元,其极限强度对船体梁总纵强度至关重要。随着计算机技术飞速发展及有限元软件功能日益强大,学者们采用非线性有限元法对船体结构极限强度开展了大量研究[1-3],这些研究大都是基于船体结构在一次性极端载荷下发生极限强度失效的理念。D．K．KIM等[4]提出了用于预测船舶加筋板结构极限强度的经验公式,并基于非线性有限元软件对该公式的准确性进行了有效性验证;XIA Tian等[5]基于非线性有限元软件对完整和开裂矩形板的极限强度进行了分析,并考虑了不同水平初始变形和焊接残余应力对极限强度的影响。

客观上,船舶在航行中必定会承受持续不断的循环波浪载荷,故针对循环载荷下的船体结构极限强度研究十分有必要。T．YAO等[6]对循环载荷下板的屈曲/塑性崩溃性能展开了研究,得出了当船体梁因极端恶劣海况达到极限强度后,应充分认识因循环波浪载荷作用下的剩余强度也十分重要的结论。因此,需要迫切分析单独的板和加筋板构件在局部崩溃后,其在循环载荷下的承载性能;许俊等[7]基于非线性有限元法,研究了焊接残余应力、测压、材料模型及循环载荷幅值耦合作用对循环载荷作用下加筋板格极限强度的影响;LI Shen等[8]指出:板与加筋板在循环载荷作用下的应力-应变曲线可用于评估其屈曲与破坏响应;CUI Huwei等[9]通过结合梁柱分析和非线性有限元法的系统计算,得到了面内循环载荷下加筋板的平均应力-平均应变关系,并将其应用于Smith法,计算了船体梁在极端循环弯矩下的极限强度;J．K．PAIK等[10]测试了一艘完工的1 900 TEU集装箱船底部加筋板在轴向循环压缩下的极限强度;崔虎威等[11]基于ANSYS非线性有限元软件,对加筋板展开了循环载荷下的极限承载性能数值模拟,分析了在循环载荷下的理想弹塑性、各向同性强化和Chaboche材料模型对加筋板极限状态下的塑性屈服区域及极限强度影响。

上述研究都有益于船体结构极限强度的高精度评估,但依然不充分,有待于进一步开展后续研究。对轴向循环载荷下船体结构极限强度研究时,大多采用的循环加载模式为等幅循环加载;但在实际海况中,波浪导致的循环载荷模式是复杂多变的,故采用等幅循环加载模式的考虑并不充分。因此,笔者基于ABAQUS有限元软件,设置了等幅循环载荷、循环载荷幅值由小到大、循环载荷幅值由大到小等3种循环加载模式;针对不同带板厚度和加强筋尺寸的扁钢加筋板开展了轴向循环载荷下扁钢加筋板极限强度数值模拟;并将扁钢加筋板循环后的极限强度与一次性极限强度进行对比分析;讨论了带板厚度、加强筋尺寸和循环加载模式对扁钢加筋板极限强度的影响。

1 有限元模型

1.1 几何尺寸与材料属性

笔者采用单根加强筋(扁钢)与带板相连接的组合模型(所选尺寸源于文献[12]的建议),扁钢加筋板几何结构与截面形式如图1,扁钢加筋板几何尺寸如表1。其中:带板分为3种厚度(分别为T1、T2、T3);加强筋分为3种尺寸(分别为S1、S2、S3)。载荷选用循环压缩-拉伸载荷;模型选用Chaboche模型(通常理想弹塑性模型没有考虑材料强化和反向加载时的鲍辛格效应,而该模型充分考虑到反向加载时材料的鲍辛格效应),模型材料参数[13]如表2。其中:C1～C3、γ1～γ3为随动强化参数;Q∞为屈服面尺寸的最大变化;B为屈服面尺寸随塑性应变发展而变化的速率。

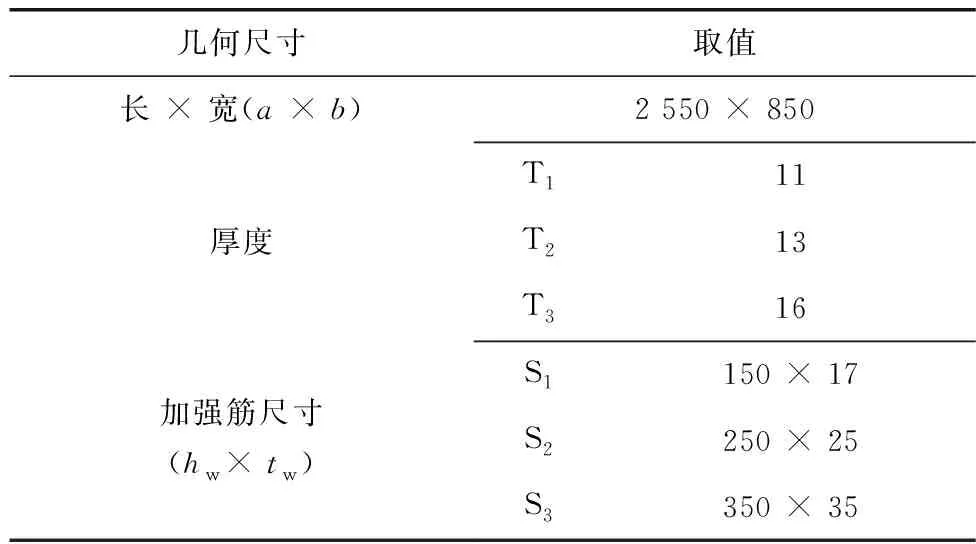
表1 扁钢加筋板几何尺寸

表2 Chaboche模型材料参数

图1 扁钢加筋板几何模型Fig. 1 Geometric model of flat-bar stiffened plate

1.2 加载模式及算例

笔者采用4种加载模式: J0为单次压缩,J1为等幅循环载荷,J2为循环载荷幅值由小到大(代表波浪载荷由弱到强),J3为循环载荷幅值由大到小(代表波浪载荷由强到弱)。每种加载模式在各自加载阶段所采用的载荷幅值及循环次数如表3。

表3 加载模式

J1、 J2、 J3加载的曲线如图2,各算例编号以“FTpSr-Jq”的形式表示。对算例编号命名解释如下。

图2 J1、 J2、 J3的加载曲线Fig. 2 Loading curves of J1, J2 and J3

1)F为扁钢加强筋。

2)Tp为带板厚度。当p=1,即Tp=T1,表示带板厚度为11 mm;当p=2,即Tp=T2,表示带板厚度为13 mm;当p=3,即Tp=T3,表示带板厚度为16 mm。

3)Sr为加强筋尺寸。当r=1,即Sr=S1,表示加强筋尺寸为150 mm × 17 mm;当r=2,即Sr=S2,表示加强筋尺寸为250 mm × 25 mm;当r=3,即Sr=S3,表示加强筋尺寸为350 mm × 35 mm。

4)Jq为加载模式。当q=0,即Jq=J0,表示加载模式为J0;当q=1,即Jq=J1,表示加载模式为J1;当q=2,即Jq=J2,表示加载模式为J2;当q=3,即Jq=J3,表示加载模式为J3。

以加载模式J0为例,表4为加载模式J0下的所有算例。

表4 算 例

1.3 初始缺陷

经过制造、加工得到的船体结构均会存在影响结构极限强度的初始缺陷[14],初始缺陷主要分为初始变形与焊接残余应力。加筋板初始变形由以下3个部分组成:

1)板的初始变形:

(1)

2)加强筋的梁柱型初始变形:

(2)

3)加强筋的侧倾变形:

(3)

笔者基于初始变形公式和二次开发的ABAQUS,通过改变有限元模型对应节点坐标,实现了初始变形的引入。扁钢加筋板截面焊接残余应力分布情况及焊接残余应力计算公式可参考文献[15]。基于焊接残余应力公式与ABAQUS预定义场结合引入焊接残余应力,以FT2S1-J0为例,施加结束初始变形和焊接残余应力的有限元模型如图3。

图3 FT2S1-J0的有限元模型Fig. 3 Finite element model of FT2S1-J0

1.4 边界条件与网格划分

采用ABAQUS有限元软件中的S4R单元建立有限元模型。加筋板作为船体结构中的重要构件,横向边界(图4中X方向)由强横梁支撑,采用简支边界条件;纵向边界(图4中Y方向)取自相邻骨材,采用对称边界条件。两横向加载端以中间节点为主节点建立刚性约束,右横向加载端限制Y方向位移,左横向加载端施加强迫位移模拟拉伸和压缩载荷,边界条件见图4。

图4 边界条件Fig. 4 Boundary conditions

单次压缩下FT2S2-J0的平均应力-平均应变曲线如图5。为兼顾精度与效率,采用25 mm×25 mm单元尺寸网格划分。

图5 3种网格尺寸的平均应力-平均应变曲线Fig. 5 Average stress-average strain curves of three kinds of mesh sizes

2 计算结果

2.1 极限状态下Von Mises应力云图

图6为FT2S1-J1、FT2S2-J1、FT2S3-J1;FT1S1-J2、FT2S1-J2、FT3S1-J2;FT3S2-J1、FT3S2-J2、FT3S2-J3等9个算例在单次压缩和循环后极限状态下的Von Mises应力云图。

图6 极限状态下的应力云图Fig. 6 Stress contour under ultimate state

在单次压缩极限状态下,塑性屈服在扁钢加筋板整体范围内均有发生;由循环后极限状态下的应力云图可发现:塑性屈服区域向扁钢加筋板中间区域集中,表明随着循环次数增加,中部区域塑性应变不断累积。由图6(a)可知:加强筋尺寸对塑性屈服区域有一定影响;当加强筋尺寸较小时,循环后的塑性屈服区域集中在加强筋上,随着加强筋尺寸增大,循环后的塑性屈服区域集中在带板上。由图6(b)可知:带板厚度对塑性屈服区域也有一定影响;当带板厚度较小时,循环后的塑性屈服区域在带板和加强筋上都有发生;随着带板厚度增大,循环后的塑性屈服区域集中在加强筋上。由图6(c)可知:循环加载模式对循环后的塑性屈服区域影响不大。

2.2 极限强度

部分算例的一次性极限强度值和经过循环载荷后的一次性平均应力-平均应变曲线及相关算例编号如图7。扁钢加筋板在单次压缩载荷下的极限强度与经过循环加载后的剩余极限强度如表5。

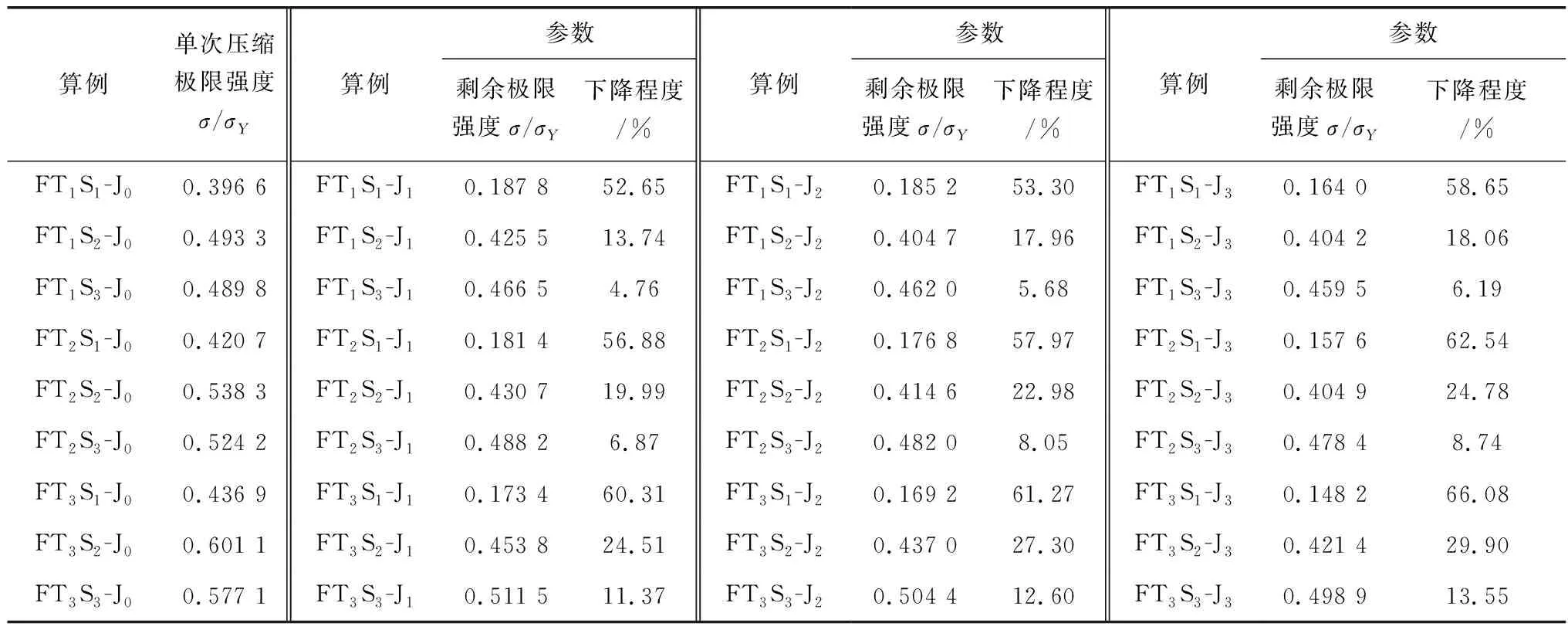
表5 极限强度对比

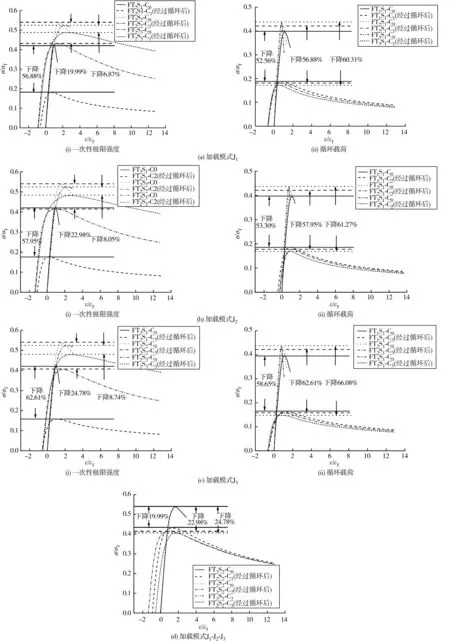
图7 扁钢加筋板平均应力-平均应变曲线Fig. 7 Average stress-average strain curves of flat-bar stiffened plates

由图7(a)可知:当加载模式为J1、带板厚度相同时,随着加强筋尺寸增大,扁钢加筋板经过循环后的极限强度下降趋势,且下降程度减缓;当加载模式为J1、加强筋尺寸相同时,随着带板厚度的增大,扁钢加筋板经过循环后的极限强度下降程度加剧。图7(b)、图7(c)中平均应力-平均应变曲线(加载模式分别为J2、 J3)也反映了相似特性,在循环载荷下,随着循环次数增加,塑性应变不断累积,扁钢加筋板极限强度不断下降。由图7(d)可看出:当带板厚度和加强筋尺寸都相同时,在循环载荷幅值由大到小的循环载荷作用下(加载模式为J3),扁钢加筋板循环后的极限强度下降了6.19%～66.08%,下降程度最大;在等幅循环载荷作用下(加载模式为J1),下降了4.76%～60.31%,下降程度最小。这表明循环加载模式对循环载荷下扁钢加筋板的极限强度有着重要影响。

3 结 论

笔者针对不同带板厚度、加强筋尺寸的扁钢加筋板,开展了单次压缩和轴向循环载荷下(3种循环加载模式)扁钢加筋板极限强度数值计算。基于初始变形和焊接残余应力,采用Chaboche模型来考虑塑性强化与鲍辛格效应;分析了循环加载模式、带板厚度和加强筋尺寸对扁钢加筋板极限强度的影响。得出如下结论:

1)在循环载荷作用下,随着循环次数增加,塑性屈服区域的塑性应变不断累积并向扁钢加筋板中部集中。当带板厚度相同时,随着加强筋尺寸增加,塑性累积从加强筋向带板转变;当加强筋尺寸相同时,随着带板厚度增加,塑性累积向加强筋处集中。

2)带板厚度相同时,随着加强筋尺寸增大,扁钢加筋板循环后的极限强度下降程度减缓。加强筋尺寸相同时,随着带板厚度增大,扁钢加筋板循环后的极限强度下降程度加剧。

3)当带板厚度和加强筋尺寸都相同时,在模式J3作用下,扁钢加筋板循环后的极限强度下降了6.19%～66.08%,下降程度最大;在模式J1作用下,极限强度下降了4.76%～60.31%,下降程度最小。