基于自适应空间差分进化算法的节能优化研究

摘 要：关注储能式列车的节能优化，通过最优化方法，在改进基本差分进化算法的基础上，应用自适应空间差分进化算法，建立求解储能式列车牵引能耗最小值的最优化数学模型，分析对列车运行能耗的影响因素。通过分析列车的牵引特性的恒牵引力-恒功率-自然特性的转折点对列车运行能耗的影响，不仅可以减低列车6.6%—9.3%的运行能耗，也可以为实际运用中的牵引特性曲线的设计提供参考。

关键词：储能式；牵引系统；能耗；最优化方法

中图分类号：TP17" " 文献标识码：A" " 文章编号：1007 - 9734 （2024） 05 - 0105 - 08

DOI：10.19327/j.cnki.zuaxb.1007-9734.2024.05.014

0 引 言

新能源轻轨列车以超级电容器为动力电源，是轨道交通领域新兴的一种形式[1]，其中列车的运行能耗主要分为两部分，分别是牵引系统能耗和辅助系统能耗[2]。由于储能式列车再生的制动能量几乎全部被回馈吸收，因此影响列车运行能耗的主要因素就集中在如何减少列车牵引能耗上[3]。此外，列车的牵引能耗还与列车的牵引特性有关[4]，对于存储能量有限的储能式牵引系统来说，关注列车的牵引特性不仅可以降低能耗，还能为实际运用中的牵引特性曲线的设计提供参考。

差分进化算法 （Differential Evolution， DE）是一种基于群体差异的启发式随机搜索算法[5]，其进化流程与遗传算法相同：初始化、变异、交叉和选择[6]。差分进化算法子代的生成采用“贪婪”的选择方式，有利于加快收敛速度，但增加了算法陷入局部最优或早熟收敛的概率[7]。1995年3月，国外作者Storn与Price撰写的差分进化算法技术报告，是差分进化算法的起源[8];1996年5月，Storn与Price在国际电机电子工程师学会演化计算研讨会上公开发布差分进化算法[9];1997年12月，Storn与Price所著的差分进化算法论文在全局优化国际学术期刊刊出[10]。2020年5月，国内作者宋克与欧阳玲等人提出了面向拟态架构的差分超时参数预测算法，既避免了统一定时不够灵活的弊端，又能自适应地解决异构执行体间的差异[11]。

为了提高差分进化算法的寻优能力、克服启发式算法常见的早熟收敛现象，需要对差分进化算法进行改进。本文提出自适应空间差分进化算法，分析对列车运行能耗的影响因素，研究重点是在列车运行线路和运行控制策略相同的情况下，寻找影响牵引能耗的因素。通过改进的最优化方法-自适应空间差分进化算法，建立求解储能式列车牵引能耗最小的最优化数学模型，进而分析列车的牵引特性中的恒牵引力-恒功率-自然特性的转折点对列车运行能耗的影响。

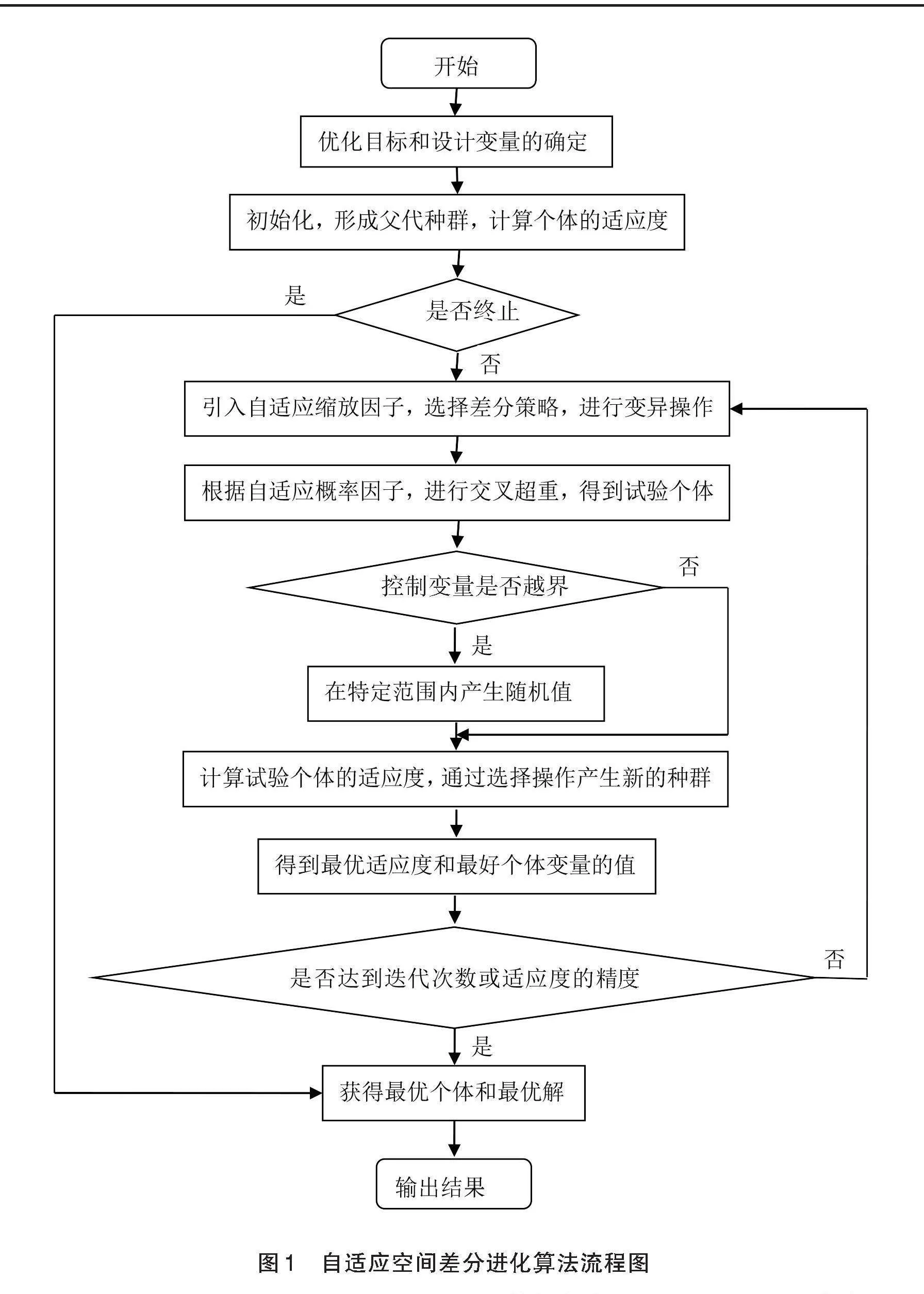
1 自适应空间差分进化算法简介

在迭代进化过程中，随着搜索空间的缩小，为了防止最优解有可能被排除在缩小后的搜索空间之外的情况发生，根据当前种群中最优解的分布位置，引入扩展空间的思想[12]，使算法能够运行在相对合适的搜索空间。不同于根据适应度控制父代杂交的遗传算法，自适应空间差分算法的变异向量由父代差分向量生成并与其个体向量进行交叉，从而生成新的个体向量并直接参与选择，而这种算法的逼近效果相比遗传算法在变异后才产生子代并被选择而言更加显著。

首先，根据基本差分进化算法，在初始化种群阶段，给定变量的初始寻优区间，随机生成种群个体[13]。经过循环迭代后，产生初始种群的区间会逐步收缩，从而推进迭代进化的进程，但是如果大部分种群个体均在相同的局部极值附近，算法容易出现暂时的停滞现象或者根本无法突破限制而陷入局部最优解，这时，就要对搜索空间进行扩展[14]。

设寻优空间为

[lk，mk=lki，mki，i=0，1，…，NP]，其中k为寻优空间的迭代次数，令k = 0，得到初始零点：

[x0i=（l0i+m0i）/2]

考虑搜索空间的上界[mk]，如果当前种群的最优个体[xki∈（mki/2，mki）]，则说明当前搜索空间的上界[mk]以及上一代搜索空间的上界[mk-1]都偏小，为了确保最优解包含在之后的搜索空间中，应该对当前搜索空间的上界[mk]进行扩展。用同样的方法，扩展搜索空间的下界[lki]。扩展规则为：

（1）若[xki∈（mki/2，mki）]，则k=k+1时，[mk+1i=2xki]；

（2）若[xki∈（lki/2，lki）]，则k=k+1时，[lk+1i=2xki]；

（3）其他情况，搜索空间则不进行扩展。

这样，经过空间扩展，迭代几次后，就会突破局部极值的限制，实现全局极优搜索。其他的变异、交叉、选择操作和自适应差分进化算法相同。

1.1" 目标函数自适应变化

在初始化确定父代种群和优化目标时，计算每个个体的适应度，该适应度等于目标函数与自适应惩罚函数项之和。自适应惩罚函数法是将自适应的思想和惩罚函数相结合，并进行了改进。表达式如式（1）所示：

[fitness（X）]=f[ （X）]+penalty[（X）]

=f[ （X）]+[λ]（k）[i=1Imax0，g（X）2+j=1Jhj[ （X）]2] （1）

式（1）中，[fitness（X）]是新的目标函数，是f[ （X）]原目标函数，[λ]（k）为自适应变化的惩罚因子，g[ （X）]和hj[ （X）]表示经过标准化处理后的约束条件。[λ]（k）的取值情况如式（2）：

[λ（k+1）=（1r1）⋅λ（k）" " " 情况1r2⋅λ（k）" " " " " " " 情况2λ（k）" " " " " " " "其他情况] （2）

式（2）中，l（k）和l（k+1）分别表示第k和k+1代的惩罚函数，情况1表示最佳个体都出现在可行域内，情况2表示都不出现在可行域内。[r1] [≻] 1.0，[r2] [≻] 1.0，并且随着优化情况不断改变自身的取值，以提高进化的效率。

1.2" 引入自适应变异缩放因子

缩放因子F用于控制差异向量的缩放程度，其取值的大小影响着进化的收敛性和收敛速度，F取较大值时，收敛速度慢，但能保证全局搜索；F取较小值时，收敛速度快，但如果取值过小，则易于陷入局部搜索，使种群过早收敛于非最优解。因此，引入一个自适应变异因子F，根据目标函数适应度的大小合理调节，从而可以有效、快速地向最优化进化。表达式如下：

[F=1- fitness（xkbest）fitness（Vki）3" ，" " "if" "fmin" " " " 1-fitness（Vki）fitness（xkbest） 3，" " "if" "fmax] （3）

式（3）中，[fitness（xkbest）]为当前种群中的最优个体[xkbest]的适应值，随着进化不断被更好的最优个体所代替；[fitness（Vki）]为当前个体[Vki]的适应值；[fmin]为目标函数的最小值；[fmax]为目标函数的最大值。

1.3" 自适应交叉概率因子

从基本差分进化算法的交叉操作可以看出，CR越大，[Vk+1ij]对[uk+1ij]的贡献越大，有利于加快收敛速度和局部搜索；反之，CR越小，[xkij]对[uk+1ij]的贡献越大，有利于保持种群的多样性和全局搜索。因此，引入一个自适应交叉概率因子CR，随着迭代次数的增加而逐渐变大，这样，在进化初期可以保证全局搜索，进化后期提高局部搜索能力。自适应交叉概率因子CR按式（4）变化：

[CR=CRmin+ni×（CRmax-CRmin）nmax] （4）

式（4）中，[CRmin]为最小交叉概率，[CRmax]为最大交叉概率，[ni]为当前迭代次数，[nmax]为最大迭代次数。

这样经过改进后，形成的自适应空间差分进化算法的流程图如图1所示。

2 自适应空间差分进化算法在储能式列车节能优化中的应用

对于储能式列车，牵引能耗的增加主要是在牵引段和维持恒速运行上。在牵引特性的恒牵引力段上，列车的加速度是最大的，列车以最大加速度加速至限速是最为节能的运行方式。在牵引特性中，恒牵引力-恒功率的转折点[v1]与电机功率相关，电机最大运用功率越大，恒牵引力-恒功率的转折点[v1]的值就越大。恒功段的加速度比自然特性的加速度要高，且列车在恒功段内单位时间的耗能是最高的，可以通过调节恒功率-自然特性的转折点[v2]来进行节能优化的研究。这样，研究储能式列车的节能优化问题，就转化为寻找牵引特性中恒牵引力-恒功率-自然特性的两个转折点的问题。由于恒牵引力-恒功率的转折点[v1]与电机最大运用功率有关，因此，问题转化为电机最大运用功率[P]和恒功率-自然特性的转折点[v2]对储能式列车牵引能耗的影响。

下面以改进的自适应空间差分进化算法，来求解储能式列车的能耗最小化问题。以牵引能耗最小为优化目标，为了减低牵引策略寻找惰行点对系统不一致的影响，牵引运行策略统一采用全力牵引-恒速-全力制动的运行模式。

优化目标：

[minW=0tP1dt=0tI（t）⋅U（t）dt" " " " " "=0tk⋅P2dt=0tk⋅F（v）⋅v（t）dt" " " " " （5）]式（5）中，W为储能式列车的牵引能耗；P1为储能式列车的超级电容电源功率，kW；I（t）为超级电容电源的电流；U（t）为超级电容电源的电压；P2为轮周功率； k为轮周功率转换为电源功率的系数；F（v）为列车的轮周牵引力；v（t）为列车的运行速度。

[s.t.F（v）-W（v）=m（1+γ）3.6⋅dvdtv（t）=0tadt0≤F（v）≤Fmax0≤v（t）≤80] （6）

式（6）中，W（v）为列车的基本运行阻力；[a]为列车的加速度；m为列车总质量；γ为列车回转质量系数；3.6表示能量转换等式1kWh=3.6×106J中的系数；80表示最高速度80km/h；F（v）的表达式如下：

[F（v）=65" " " "（kN）" "0km/h≤v≤v1km/hP2×3.6v" "（kN）" "v1km/h≤v≤v2km/hP2×3.6×v2v2（kN）" "v2km/h≤v≤80km/h] （7）

[Fmax=mgμ] （8）

[W（v）=516+m×0.00637 +0.000329×v+8.109×v2/1000] （9）

式（7）、式（8）及式（9）中，v1为牵引特性的恒牵引力-恒功率的转折点；v2为牵引特性的恒功率-自然特性的转折点；μ为黏着系数；W（v）为主机厂提供的基本阻力计算公式。

[k=1/η1/η2/η3" " " " " case1η1⋅η2⋅η3⋅η4" " " " " case2] （10）

[P2=4P0=P-100200（U-550）+100 （kW） ，550V≤U≤750VP（kW），" " " " " " " " " " " " " " " " " " " " " " " " "U≥750V] （11）

式（11）中，η1为电机效率0.98，η2为逆变器效率0.98，η3为齿轮传动效率0.98，η4为电源充电效率0.9，P为电机最大运用功率。

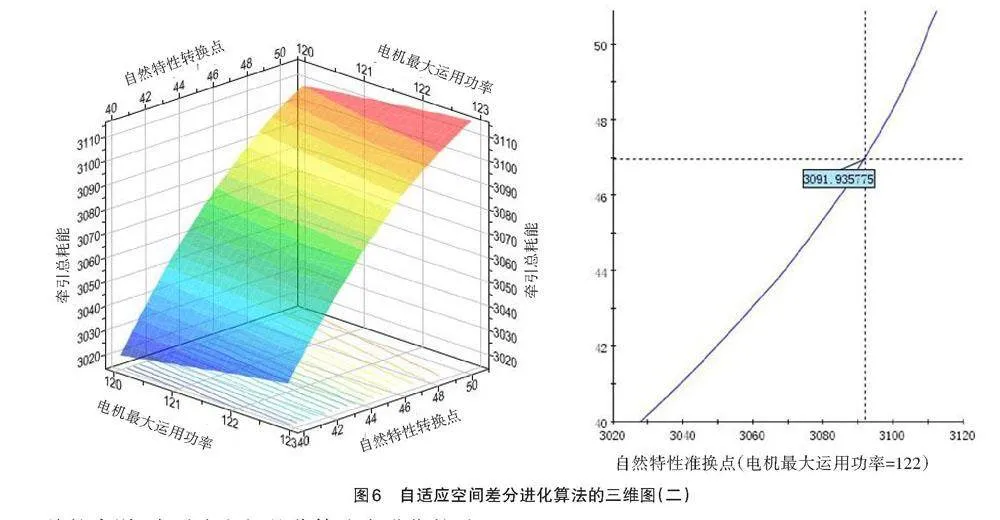
基于自适应空间差分进化算法，设置4个输入变量，分别是列车最高运行速度[vmax]、电机最大运用功率[P]、恒功率-自然特性的转折点[v2]及列车牵引质量m。设置[vmax=80]km/h，[P∈（120，150）]，[v2∈（40，60）]，[m∈（44.5，63.1）]，超级电容电压[∈（550，900）]，列车最大运行距离为1500m。随机数种子为75，点群规模为20，最大迭代次数为30，最小扩展空间基准的最大迭代次数为5，缩放系数为0.9。以自适应空间差分进化算法运行后，求得最优解最小牵引能耗为2.82kWh，此时，电机最大运用功率[P]为120kW，自然特性的转折点[v2]为40 km/h，列车最高运行速度为78.3 km/h，列车牵引质量为44.5t。迭代过程计算了500次。算法的直观计算过程和输出结果，如优化进程、三维散点图和解的三维图，分别如图2—图6所示。

散点图可以直观描述变量之间的相关性，图3描述了自然特性转换点、列车质量与牵引总能耗之间的关系，而图4则描述了自然特性转换点、电机最大运用功率与牵引总能耗之间的关系。从图2可以看出，自适应空间差分算法在进化的过程中，随着迭代次数的增加而逐步趋向于局部最优解。从图3、图4可以看出，牵引能耗与自然特性、电机最大功率及列车质量在不同区间内各自存在一定的线性关系，但电机最大运用功率对散点分布影响较大，即牵引能耗 随着电机最大运用功率和自然特性的转折点增大而增加。因此要想牵引能耗最小，就要减小电机最大运用功率，并尽早实现恒功率-自然特性段的转换。

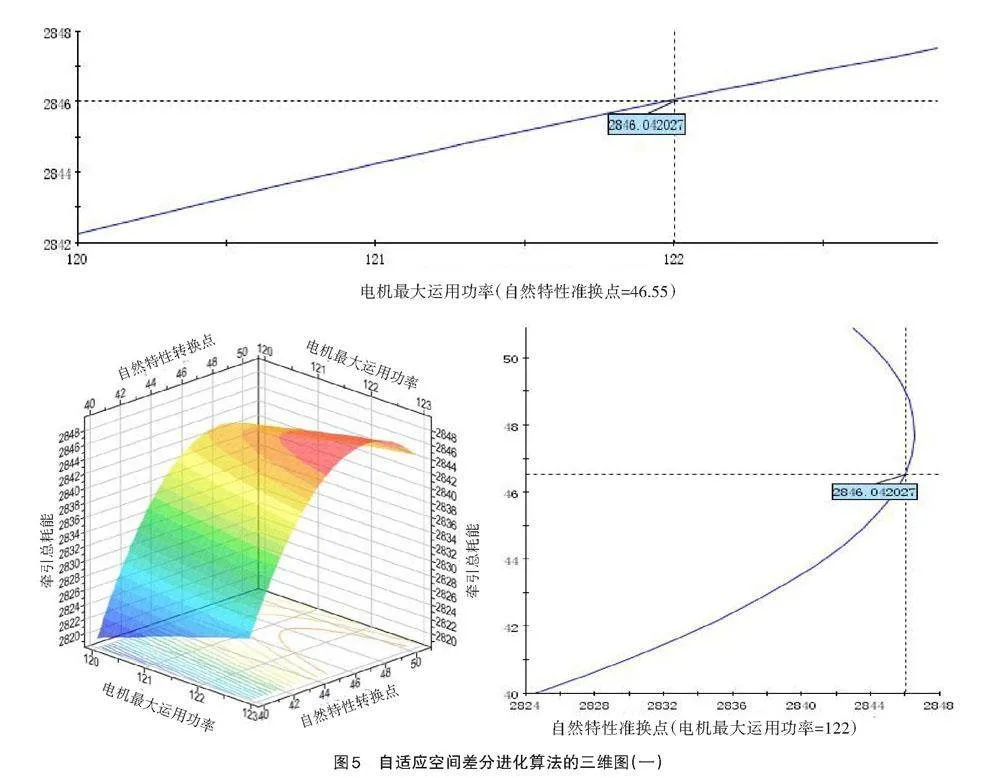
图5为当列车最高运行速度为80km/h、列车牵引质量为44.5t时，电机最大运用功率、自然特性转换点与牵引总能耗的关系图。

从图5可以看出，当列车牵引质量为44.5t时，自然特性转换点[v2]从40km/h增大到48km/h，牵引总能耗逐渐增加；之后，牵引总能耗又逐渐减小，为非线性变化；牵引总能耗在2.82kWh和2.85kWh之间。即通过自适应空间差分进化算法，优化过程易于根据优化情况进行自身调整，从而得到一个全局最优解，避免了基本差分进化算法对算法控制参数依赖过大的缺陷。

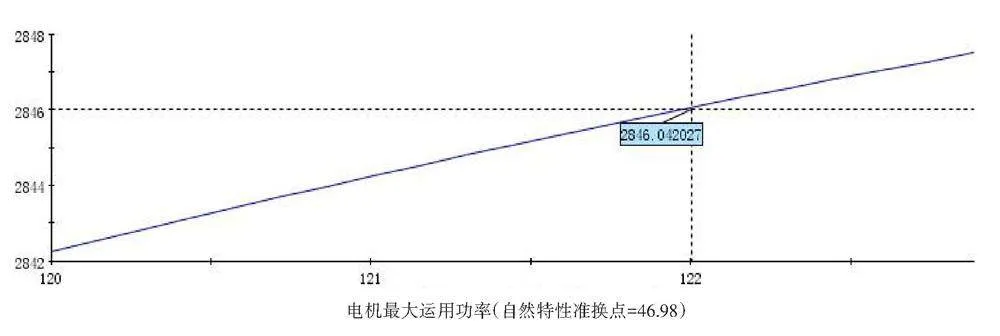
从图6可以看出，当列车牵引质量为60.7t且自然特性转换点[v2]为46.98km/h时，由电机最大运用功率图可知，随着电机最大运用功率[P电机]的增大，牵引总能耗由3.085kWh逐渐增加到3.091kWh。而电机最大运用功率[P电机]为122kW时，由自然特性转换点图可知，随着牵引总能耗的增大，自然特性转换点[v2]也逐渐增加，且在牵引总能耗达到3.091kWh时，自然特性转换点[v2]为46.98km/h。从三维图可以看出，当列车牵引质量为60.7t时，随着自然特性的转换点[v2]和电机最大运用功率[P电机]的增大，牵引总能耗也逐渐增加，由3.02kWh增加到3.11kWh。

lt;E：＼2023田田＼10--＼郑州航空工业管理学院学报202405＼Image＼李图片5a.pnggt;[电机最大运用功率（自然特性准换点=46.98）]

总的来说，自适应空间差分算法在进化的过程中，对种群的搜索空间进行了自适应的扩展，因此使得算法可以克服基本差分进化算法易于陷入局部最优解的缺点，进化过程有规律地进行，最后得到最优解。

3 结 论

本文针对基本差分进化算法易于陷入局部最优解的缺点，运用了一种自适应空间搜索策略，得到一种改进的自适应空间差分算法。在迭代的进化过程中，随着搜索空间的缩小，为了防止最优解有可能被排除在缩小后的搜索空间之外的情况发生，根据当前种群中最优解的分布位置，引入扩展空间的思想，使算法能够运行在相对合适的搜索空间。采用了自适应进化策略，包括自适应变异因子和自适应交叉概率因子，使得这些控制参数在优化迭代的过程中，可以根据优化情况，不断调整自身的数值大小，从而达到较高的寻优成功率和较快的收敛速度。通过改进的最优化方法-自适应空间差分进化算法，建立求解储能式列车牵引能耗最小的最优化数学模型，分析列车的牵引特性的恒牵引力-恒功率-自然特性的转折点对列车运行能耗的影响。

参考文献：

［1］刘友梅.轨道电力牵引新能源策略的思考[J].电力机车与城轨车辆，2012，35（5）：1-4.

［2］杨颖，陈中杰.储能式电力牵引轻轨交通的研发[J]. 电力机车与城轨车辆，2012（8）：7-16.

［3］VICTOR I H， HAIZEA G.Optimal energy management and sizing of a battery-supercapacitor-based light rail vehicle with a multiobjective approach[J].IEEE Transactions on Industry Applications，2016，52（4）：3367-3376.

［4］FARHADI M， MOHAMMED O.Adaptive energy management in redundant hybrid dc microgrid for pulse load mitigation[J]. IEEE Trans. Smart Grid， 2015，6（1）： 54-62.

［5］李明.详解matlab在最优化计算中的应用[M].北京：电子工业出版社，2011.

［6］陈少真，付志新，任炯炯.减轮Serpent算法差分-线性分析的新结果[J].信息工程大学学报，2020，21（6）：699-704.

［7］邓阳，陈洪根，黄春雷，等.基于数值分析和神经网络的轨道过车信号判断[J].郑州航空工业管理学院学报，2022，40（1）：106-112.

［8］STORN R，PRICE K. Differential evolution ： a simple and efficient adaptive scheme for global optimization over continuous spaces[R].ICSI Technical Report TR-95-012， March 1995.

［9］STORN R，PRICE K.Minimizing the real functions of the ICEC'96 contest by differential evolution，in Proceedings of IEEE international conference on evolutionary computation[J].Nagoya， Japan，1996，5： 842-844.

［10］STORN R，PRICE K. Differential evolution：a simple and efficient heuristic for global optimization over continuous spaces[J].Journal of Global Optimization，1997，11（4）：341-359.

［11］宋克，欧阳玲，魏帅，等.面向拟态架构的差分超时参数预测算法[J].信息工程大学学报，2020，21（4）：470-475.

［12］李玲，唐嘉成，谭皓琳.一种小型无人机飞行控制及图像传输系统设计研究[J].郑州航空工业管理学院学报，2024，42（2）：58-64.

［13］董磊.基于Lasso算法的临空高科技产业选择与入区评价研究[J].郑州航空工业管理学院学报，2021，39（1）：5-16.

［14］陈新溅，陈中杰，陈超录，等.储能式电力牵引轻轨车电气牵引系统研制[J].机车电传动，2013（1）：73-77.

［15］吴寅成. 基于自适应进化策略的加筋板结构可靠性优化[D].大连：大连理工大学，2011.

［16］吴亮红，王耀南，袁小芳，等.自适应二次变异差分进化算法[J].控制与决策，2006，21（8）：898-902.

责任编校：刘 燕，孙咏梅

Energy-saving Optimization Based on Adaptive Space

Differential Evolution Algorithm

LI Ling1，2，HUANG Chenxu1，TAN Haolin1，LIANG Ziang1，REN Feng3

（1.School of Automation，Zhengzhou University of Aeronautics，Zhengzhou 450046，China；

2.Henan Engineering Research Center of Aeronautics and Astronautics Guidance and Control，Zhengzhou 450046，China；

3.Xi’an Jiasheng Intelligent Manufacturing Technology Co.，Ltd，Xi’an 710021，China）

Abstract： This paper focuses on the energy-saving optimization study and establishes the optimization mathematical model to solve the minimum value of traction energy consumption of the energy storage typed train. This paper analyzes the influence factors of energy consumption of train operation by the adaptive space differential evolution algorithm. It analyzes the turning points of the tractive characteristics influence on train operation energy consumption，between constant traction， constant power and natural characteristic. This can not only reduce the operation energy consumption of the train by 6.6% to 9.3%， but also can provide the reference for the design of the traction characteristic curve in practical application.

Key words：energy storage type；traction system；energy consumption；optimization methods

收稿日期：2023-12-18

基金项目：河南省科技攻关项目（212102210491）；河南省杰出外籍科学家工作室（GZS2022011）资助

作者简介：李 玲，女，山东威海人，博士，副教授，硕士生导师，研究方向为电力牵引与控制。