基于均衡张量与非凸函数的高精度低秩张量恢复方法

摘 要：基于最小化核范数之和的低秩张量恢复方法已在许多领域取得广泛应用，但在某些应用场景，如彩色视频恢复中，其恢复结果不够理想，尤其是当已知元素数目较少时，恢复结果更差。导致该问题出现的一个根本原因是张量的不均衡结构，即张量中某些模的维度远小于其他模，这使得其展开矩阵是一个极度不均衡且满秩或高秩的矩阵。此外，秩的凸松弛则是导致该问题出现的另一个重要原因，最新研究表明，一些非凸函数可以比核范数更好地逼近秩。基于上述考虑，首先，引入一个重构操作将不均衡张量重构为更加均衡的张量，该重构操作能在保留张量低秩特性的同时减少算法准确恢复所需的已知元素数目；其次，将非凸logDet函数引入低秩张量恢复算法中，以取得比核范数更好的秩逼近效果；最后，通过与其他经典算法在彩色视频上开展对比实验，充分验证了本方法的有效性。

关键词：图像处理；低秩张量恢复；均衡张量；logDet 函数

中图分类号：TP391" "文献标识码：A" "文章编号：1007 - 9734 （2024） 05 - 0097 - 08

DOI：10.19327/j.cnki.zuaxb.1007-9734.2024.05.013

0 引 言

作为向量和矩阵的高阶拓展，张量能够充分利用数据的多线性结构来提供更好的数据分析和理解。近年来，张量已经被成功应用于各种不同的领域，如信号处理[1]、计算机视觉[2]、数值分析[3]、数据挖掘[4]等。其中，低秩张量恢复算法因其能充分利用数据的低秩特性实现数据的补全和预测，受到广泛关注[5]。而张量秩的定义在低秩张量恢复算法中起到了至关重要的作用，与矩阵的秩相比，张量的秩要更复杂。目前，张量秩有两种定义被广泛接受，即CP秩[6]和Tucker秩[7]，它们分别是基于CP分解和Tucker分解发展而来。其中，CP秩的求解被证明是一个NP难问题[8]，因此现有研究多集中于Tucker秩，即张量各展开矩阵的秩的集合。进一步，通过使用核范数替换秩，Tucker秩的求解可近似表示为计算各展开矩阵的核范数之和[9]。通过深入分析基于最小化核范数之和的低秩张量恢复方法在图像恢复[10]、视频恢复[11]等领域的应用，我们发现其恢复结果不够理想，尤其是当已知元素的数目较少时。

针对这一问题，在前期研究中[12]将其归结于张量的不均衡结构。以彩色视频为例，该张量第三个模的维度固定为3，远小于其他模的维度，这种不均衡结构会导致出现一个极度不平衡且满秩的展开矩阵，而满秩矩阵并不适用于低秩优化方法，会对恢复结果造成影响。同时，该研究还针对性地提出了一种重构操作，以获取更均衡的张量。实际上，对张量的结构进行改变还出现在文献[13]中，该研究将张量直接展开为矩阵进行计算，此方法虽然可以消除不均衡结构带来的影响，但过于剧烈的结构变化也会导致部分结构信息的丢失。此外，基于最新关于TT秩的研究，文献[14]选择将张量重构为更高阶的形式，并使用一系列较为均衡的矩阵的秩来表示张量秩。该方法由于有着较为严格的条件限制，目前在除了数学和物理领域之外的应用较少。

此外，近期有研究认为导致算法恢复精度不理想的另一个重要原因在于秩的凸松弛，该方法并不总是有效的，甚至可能导致偏差[15]。文献[13]的研究表明，理想的非凸函数方法与凸松弛方法之间在正确恢复所需已知元素的数量方面存在较大差距。因此，一些非凸函数，如logDet[16-17]和加权核范数[18]，受到了越来越多的关注，实验表明，这些非凸函数能取得比核范数更好的恢复结果。文献[19]则进一步证明，当使用[lp（0lt;plt;1）]范数替换 [l1]范数时，可以在已知元素较少时更为精确地完成张量重构。

受上述研究的启发，本文创新性地将均衡张量和非凸函数相结合，提出了一种混合低秩张量恢复方法，以获得更高的恢复精度。

1 理论背景

1.1" 张量基础

本文中，标量使用非粗体小写字母表示，例如x；而对于向量，使用粗体小写字母表示，例如x；为了便于区分，本文使用非粗体大写字母表示矩阵，例如 X，而对于张量，则使用粗体大写手写体字母表示，例如[X]。因此，对于N 阶张量，本文表示为 [X] [∈RI1×I2×…×IN]。

定义1（张量展开及Tucker秩） 张量[X]第[n]个模的展开矩阵表示为[X（n）] = unfoldn（[X]） [∈] [RIn×i≠nIi]，该矩阵的列是[X]的第[n]个模的纤维按顺序排列构成。与之相应的，张量展开的逆运算符表示为 “fold”，即[X]= foldn（[X（n）]）。

N阶张量的Tucker秩被定义为该张量所有展开矩阵的秩的集合，其表示为：

ranktc（[X]） = （rank（[X（1）]），...，rank（[X（N）]））

只有当所有展开矩阵[Xn，i=1，...，N]都是低秩矩阵时，张量[X]才是低秩张量。

定义2[12]对于一个秩为[ranktcX][=（r1，r2，…，rL）]的L阶张量[X∈Rn1×n2×…×nL]，假设张量所有模的索引被分为两个集合[F=i1，i2，…，ij⊂L={1，2，…，L}] 和[ J=L-F={ij+1，ij+2，…，iL}]，如果对于任意[im∈F]和[ij∈J]，都有[nim≪nij]，且[im]对应模的展开矩阵是满秩或高秩，即[ ∆q=nim-rim]是一个接近0的小整数，那么，张量[X]被称为非均衡张量，对应的模 [im]为其非均衡模。

根据上述定义可知，对于非均衡张量，其不均衡模的展开矩阵为高秩或满秩矩阵。以彩色视频为例，该数据为典型的四阶非均衡张量，其中第三个模代表颜色信息，其维度固定为3，且远小于其他模的维度。

推论1[20]（矩阵恢复条件）对于秩为[r]的矩阵[A∈Rj×k] ，存在常数[c0， c1gt;0]，使得当已知元素数目满足条件[ m≥c0r（j+k）log （jk）]时，矩阵[A]能以至少[（1-e-c1m）]的概率通过最小化核范数方法实现准确恢复。

由推论1可知，矩阵的秩越大，使用最小化核范数方法恢复所需的已知元素数目越多，且准确恢复的概率越小。结合前文给出的非均衡张量定义可知，非均衡模对应的满秩或高秩展开矩阵需要更多的已知元素才能准确恢复，这是导致张量整体恢复精度不理想的一个重要原因。

1.2" 低秩张量恢复

对于[L]阶张量[X∈Rn1×n2×…×nL]，其Tucker秩为[ranktc（X）=（rankX1，…，rankXL）]，通过充分利用张量的低秩特性，根据部分已知元素来补全张量，其低秩优化模型为：

[minX rankX" "s.t." PΩX=B] （1）

其中 [X，B∈Rn1×n2×…×nL]是[L]阶张量，Ω是张量已知元素的索引集合，[PΩ]（·）是一个采样运算符，用于保持索引在Ω中的元素值不发生改变。

在上述模型中，函数[rank]（·）是离散的且非凸的，要获得其全局最优解是一个NP难问题。因此，与低秩矩阵优化方法类似，通过使用核范数替换秩，可将该问题转化为凸优化问题：

[minX" X*=1LαiX（i）*s.t." PΩ（X）=B.] （2）

其中，常数[αi]满足[αi]≥0 并且[1Lαi]= 1。

推论2[21]（张量恢复条件）对于张量[ X∈Rn1×n2×…×nL]，假设[ n1=…=nL=n，] [rankX1=…=rankXL=r] 。要想通过最小化各展开矩阵的核范数之和来正确恢复[X]，其已知元素的数目需满足条件[ m≥CrnL-1]，其中[C ]为常数。

需要注意的是，推论2中已知元素需要满足的条件[CrnL-1]实际上与秩为[r]，维度大小为[n×nL-1]的展开矩阵密切相关。 因此，对非均衡张量而言，如彩色视频，其非均衡模的展开矩阵为高秩或满秩矩阵，这也意味着需要更多的已知元素才能正确恢复张量，再次验证张量不均衡结构是导致其恢复结果不理想的主要原因之一。

2 本文研究方法

如前文所述，张量的不均衡结构和秩的凸松弛是导致基于核范数之和的低秩张量恢复方法结果不理想的主要原因。为了解决该问题，本文首先给出一个重构操作来构建均衡张量，以减少不均衡结构带来的影响；其次，引入非凸logDet函数作为比核范数更好地秩逼近。通过将均衡张量与非凸函数相结合，本文提出一种高精度低秩张量恢复的方法，具体的技术路线如图1所示。

2.1" 重构均衡张量

对于给定的非均衡张量[X∈Rn1×…×ni×…×nL， ]其中，[ni]表示非均衡模的维度大小。为了将第[ i ]个模与第[ k ]个模合并，本文给出一个重构操作[ Ti，kX，k=1，2，…，L，k≠i]，重构后的均衡张量[ X=Ti，kX∈Rn1×…nz…×nk-1×nk+1…×nL，nz=（nink）]为[L-1] 阶张量。

[X=Ti，kX= ]

[reshape（X，[n1，…，ni…，nk，nk-1，nk+1，…，nL]）] （3）

需要注意地是，对于包含有多个非均衡模的张量，重构操作 [Ti，j（）]依然适用：

[Ti1，i2，jX=Ti2，i1，jX=Ti1，jTi2，j（X）] （4）

其中，[i1，i2]是不均衡模。

为了便于理解，本文以一个四阶非均衡张量为例：假设原非均衡张量为[ X∈Rn×n×m×n，m≪n]，其秩为[ ranktc（X）≤（r，r，m，r）]，根据上述定义，重构后的张量为[ X=T3，4（X）∈Rn×n×（mn）]。

根据文献[22]，经过重构操作后，可以减少准确恢复张量所需的已知元素数目。还是以上述四阶非均衡张量为例，假设用[M（Xi）]表示展开矩阵准确恢复所需的已知元素数目，可知：

[M（X3）=Cm（n3+m）] （5）

[M（X2）=Cmr（n2+mn）] （6）

计算两者之间的差异可得：

[MX3-MX2=Cmn2n-r+Cm2-Cm2rngt;Cmn2n-r-Cm2rn=Cmn（nn-r-mr）] （7）

考虑到[rlt;n] 及 [n-rgt;m]，可知：

[MXilt;MXi] （8）

2.2" 非凸 logDet 函数

非凸logDet函数最早应用于低秩矩阵恢复方法中，其优化模型可表示为：

[minX logDet（X+I）s.t." PΩ（X）=M] （9）

其中，X[∈Rn×n 是一个正矩阵，Ω为]已知元素的索引集合，[Ι] 是单位矩阵。

本文考虑将非凸logdet函数引入低秩张量恢复方法中的一个重要原因是其能比核范数更好地逼近秩，即

[logDetX+Ilt;X*] （10）

接下来将就此给出证明。

首先，分别根据各自定义，可得：

[logDetX+I=logi=1nσiX+1=i=1nlogσiX+1" ] （11）

[X*=i=1nσiX] （12）

其中，[σiX]为矩阵[X]的奇异值。

其次，构建一个新的函数：

[f（X）=logσiX+1-σiX] （13）

对该函数求一阶导可得：

[df（X）dσiX=1σiX+1-1] （14）

可知，当[σiXgt;0]时， [f（X）]为单调减函数，即有[f（X）lt;f（0）]=0。由此可知，非凸logDet函数是比核范数更紧致的秩逼近。

特别地，当矩阵只包含一个非零奇异值时，其秩固定为1，此时核范数的大小会随着奇异值的大小发生线性变化，而非凸logDet函数的结果曲线则更加接近秩，即比核范数更好地逼近秩。两者的对比结果如图2所示。

2.3" 混合模型

首先，对于给定的[L]阶非均衡张量[X∈Rn1×…×ni×…×nL]，其中，第[i]个模为非均衡模，通过前文给出的重构操作，构建一个均衡张量[X]：

[X=]

[Ti，i+1X =reshape（X，[n1，…，nini+1，ni+2…，nL]）] （15）

其次，将非凸logDet函数引入低秩张量恢复方法中，其低秩优化模型可表示为：

[minX X*=i=1LαilogDet（X（i）XT（i）12+I）s.t." PΩ（X）=G] （16）

其中，[X]是重构后的均衡张量，[αi] 是常量参数，且满足[αi≥0]和[i=1Lαi=1]。

为了简化表达式，定义[F（V）]函数 ：

[F（V）=logDet（（VVT）12+I）=log∏Ini=1（σi（V）+I）=∑Ini=1log（σi（V）+I）] （17）

此外，对张量[X]进行变量分离，给出新的变量[Yi=X，i=1，2，⋅⋅⋅，N。]考虑到在很多应用场景中，张量元素都是非负的，进一步如非负约束。

最后，本文提出的混合低秩张量恢复模型为：

[minYi" i=1LαiF（Yi，（i））s.t." X=Yi，i=1，2，…，LPΩ（X）=G] （18）

3 求解框架

使用交替方法乘子法求解上述模型，首先，对张量[X]定义一个简单约束[∆={X：PΩ（X）=G，X≥0}]，该约束将在后续求解[X]时使用，其次，将优化模型表示为增广拉格朗日函数：

[LYi，X，X∈△，Mi]

[=i=1LαiFYi，i+i=1Lu2" Yi-X2F]

[+i=1Llt;Mi， Yi-Xgt;] （19）

其中，惩罚因子[μgt;0]，[Mi∈RI1×I2×⋅⋅⋅×IL]是拉格朗日乘子。

最后，通过将[LYi，X，X∈△，Mi]函数中除某一个变量之外的其他变量视为常量，从而对该变量进行迭代更新，使得函数[LYi，X，X∈△，Mi]取最小值，重复上述步骤，依次更新不同的变量，其整体迭代优化步骤如下：

[Step 1： Yk+1i←arg minLYi，Xk，MkiStep 2： Xk+1←arg minLYk+1i，Xk，MkiStep 3： Mk+1i =Mki+u∂LYk+1i，Xk+1，Mki]

A.更新变量[Yk+1i]。

该子优化问题为：

[Yk+1i][=argminYiαiFYi，i+u2 Yi-X+Miu2F] （20）

根据文献[23]，该子优化问题等价于：

[σ*n=arg minσnfσn+β2αnσn- σVn2F）] （21）

其中，[σ*n={σ*1，n，…，σ*i，n}]，[ σXn=σ1，Xn，…，σi，Xn]分别为矩阵[Yi，i]和[（Xi-Mi，iu）]的奇异值。

根据一阶最优解条件，目标函数相对于每一个奇异值的梯度都应该消失，因此，针对每一个奇异值可求其最优解：

[σ*i，n∈{11+σi，n+βαnσi，n-σi，Vn=0 }] （22）

最后，变量[Yk+1i]最优解如下：

[Yk+1i=Fold（ Udiagσ*nVT）] （23）

其中，[Xi-Mi，iu=Udiag σXnVT]。

B.更新变量[Xk+1]。

该子优化问题为：

[Xk+1=argminXi=1Lu2 Yi-X+Miu2F] （24）

注意到该目标函数是一个强凸二次函数，其最优解可通过直接求一阶导获得，同时，还需要考虑变量[X]的约束条件[∆]，即保持已知元素的值不变。

最后，变量[Xk+1]的最优解如下：

[Xk+1=1L1L（uYi+Mi）+， xi1，i2，…iL∉Ω" " " " " G" " " " ， xi1，i2，…iL∈Ω] （25）

C.更新变量[Mk+1i]。

该子优化问题为：

[Mk+1i =Mki+u∂LYk+1i，Xk+1，Mki] （26）

其最优解为：

[Mk+1i =Mki+uYi-X] （27）

上述迭代求解过程可通过改变惩罚因子[u]的取值来加速，在本文中，设置乘子[t=1.05]，即有[uk+1=tuk]，具体的求解框架如算法1所示。

[算法1 混合低秩张量恢复方法 输入：张量[G]，索引集合[Ω]，惩罚因子[μ，]最大迭代次数Maxiter，迭代停止条件Tol 初值：[Yi=Mi=0，iϵ{1，2，…，L}] 1： for n=1 to Maxiter do 2： for i=1 to L do 3： 根据公式 （23） 更新 [Yk+1i] 4： end for 5： 根据公式 （25） 更新 [Xk+1] 6： for n=1 to L do 7： 根据公式 （27） 更新[Mk+1i] 8： end for 9： 收敛条件[Xk+1-Xk][F/XkFlt;Tol] 10： end for 输出： [X] ]

4 实验分析

本文所有实验均在同一环境下进行，计算机配置为AMD Ryzen 5 3500U，频率为2.10GHz，内存为 8GB，操作系统为Windows 10，使用的Matlab版本为9.5.0.944444（R2018b）。

两种典型的基于Tucker秩的低秩张量恢复方法，HaLRTC[24]和LogDet[25]，被用来与本文方法进行对比。其中，HaLRTC是一种被广泛使用的基于核范数之和的凸松弛方法，该方法已经被证明在精度和效率上都有着较好地表现；而LogDet则是一种基于非凸函数的方法，其在恢复精度上有着出色的表现。

本文选取最典型的四阶非均衡张量和彩色视频来验证本文提出方法的有效性。所有的测试视频均可通过链接http：//trace.eas.asu.edu/yuv/下载。本文首先将YUV格式视频转换为RGB格式，再将其表示为四阶张量。同时出于计算效率的考虑，只选取视频前150帧图片进行实验，因此，实验数据大小为[144×176×3×150]。需要强调的是，在重构均衡张量时，为了使新的张量仍然有意义，选择将张量最后两个模合并。

此外，除相对误差与时间，本文还通过峰值信噪比（PSNR）来量化张量恢复的精度：

[PSNRX，T=10log10nT2maxX-T2F ]。

根据表1和图3中的实验结果可得出如下结论：（1）对于所有视频和采样率，本文方法都能取得比另外两种方法更高的恢复精度，尤其当采样率较低时，其他两种方法与本文方法的差距较大；（2）通过引入均衡张量，本文方法能进一步提高logDet方法的恢复精度；（3）HaLRTC方法效率最高，logDet方法由于引入非凸函数，其计算复杂度较高，计算成本比HaLRTC方法更高；（4）由于引入均衡张量，展开矩阵的规模增大，本文方法计算成本进一步增加，略高于logDet方法。

此外，为了更直观地对比不同方法的恢复结果，本文在图4中分别展示了视频“Phone”和“Hall”在各种采样率下的恢复结果。其中，从左到右依次为原始图片、采样图片以及由HaLRTC、LogDet和本文方法恢复的图片。需要注意地是，每一个视频结果中从上到下依次为采样率为10%的第60帧图片，采样率为20%的第90帧图片，采样率为30%的第120帧图片。从结果可以看出，本文方法的恢复结果要优于其他两种方法，能恢复更多的图片细节，尤其是在采样率较低时，其恢复效果更好。

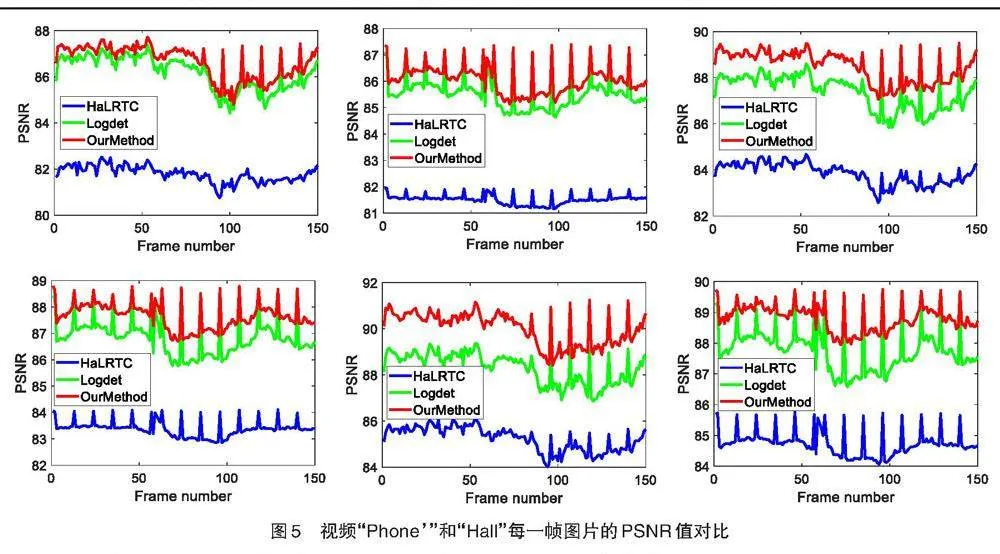
最后，为了更全面地描述不同方法的恢复质量，本文在图5中分别给出了两种视频所有图片在不同采样率下的PSNR值，从上到下的采样率依次为10%、20%和30%。从结果可以看出本文方法能取得更好的恢复效果。

此外，为了进一步验证本文方法的可靠性，本文还在更多的视频数据上进行了实验，实验结果如表2所示。

5 总 结

本文针对基于核范数之和的低秩张量恢复方法在某些应用，尤其是彩色视频恢复中结果不理想的问题进行了深入思考，并提出一种均衡张量与非凸函数相结合的高精度低秩张量恢复方法。一方面通过引入重构操作，以构建更均衡的张量，从而解决不均衡结构带来的影响；另一方面通过引入非凸logdet函数作为比核范数更紧致的秩逼近，从而进一步提高算法的恢复精度。随后，为了更全面地了解所提出方法，将其与其他经典算法进行了对比，在不同彩色视频中的实验结果验证了本文方法的有效性。最后，由于构建均衡张量会导致展开矩阵规模增大，同时引入非凸函数会进一步增加计算复杂度，因此导致本文方法的计算成本较高，后续作者将进一步探究如何提高该方法的效率。

参考文献：

［1］田振.低秩稀疏恢复理论研究及其在信号处理中的应用[D].武汉：武汉科技大学，2023.

［2］虞涛.基于低秩稀疏分解的遮挡人脸识别研究[D].南京：南京邮电大学，2020.

［3］杨磊.低秩张量恢复问题的数值算法研究[D].天津：天津大学，2014.

［4］MØRUP M.Applications of tensor （multi-way array） factorizations and decompositions in data mining[J].Wiley Interdiscip.Rev.-Data Mining Knowl.Discov，2011，1（1）：24-40.

［5］刘园园.快速低秩矩阵与张量恢复的算法研究[D].西安：西安电子科技大学，2013.

［6］XU H，ALBERA L，KACHENOURA A，et al.Low rank canonical polyadic decomposition of tensors based on group sparsity[C].European Signal Processing Conference，2017：668-672.

［7］SILVA C D，HERRMANN F J.Optimization on the hierarchical tucker manifold applications to tensor completion[J].Linear Algebra Its Applications，2015，481：131-173.

［8］KOLDA T G，BADER B W.Tensor decompositions and applications[J].SIAM Rev，2009，51（3）：455-500.

［9］GANDY S，RECHT B，YAMADA I.Tensor completion and low-n-rank tensor recovery via convex optimization[J].Inverse Probl，2011，27：25010.

［10］MOHAOUI S，HAKIM A，RAGHAY S.Smooth tensor robust principal component analysis with application to color image recovery[J].Digital Signal Processing，2022，123：103390.

［11］YANG L，KOU K I，MIAO J，et al.Quaternion tensor completion with sparseness for color video recovery[J].Applied Soft Computing，2024：111322.

［12］SHI C，HUANG Z，WAN L.An effective approach for color video recovery based on balanced tensor[J].Signal Processing：Image Communication，2019，78：376-387.

［13］MU C，HUANG B，WRIGHT J.Square deal：lower bounds and improved relaxations for tensor recovery[C].Proceedings of International Conference on Machine Learning，2013：73-81.

［14］BENGUA A，PHIEN N，TUAN D.Efficient tensor completion for color image and video recovery：low-rank tensor train[J].IEEE Trans.Image Process，2017，26（5）：2466-2479.

［15］KANG Z，PENG C，CHENG Q.Robust PCA via non-convex rank approximation[C].IEEE International Conference on Data Mining，IEEE Computer Society，2015：211-220.

［16］SHI C，HUANG Z，WAN L，et al.Low-rank tensor completion based on log-det rank approximation and matrix factorization[J].Journal of Scientific Computing，2019，80（3）：1888-1912.

［17］KANG Z，PENG C，CHENG Q.Top-N recommender system via matrix completion[C].Proceedings of the AAAI Conference on Artificial Intelligence，2016.

［18］GU S H，ZHANG L，ZUO W M.Weighted nuclear norm minimization with application to image denoising[C].Proc.CVPR IEEE，2014：2862-2869.

［19］LIU C S，SHAN H，CHEN C L.Tensor p-shrinkage nuclear norm for low-rank tensor completion[J].Neurocomputing，2020，387（3）：255-267.

［20］RECHT B，FAZEL M，PARRILO P A.Guaranteed minimum-rank solutions of linear matrix equations via nuclear norm minimization[J].SIAM Rev，2010，52（3）：471-501.

［21］TOMIOKA R，SUZUKI T，HAYASHI K.Statistical performance of convex tensor decomposition[C].Proceedings of Advances in Neural Information Processing Systems，2011：972-980.

［22］石承飞.基于非凸低秩优化的数据处理方法及应用研究[D].武汉：华中科技大学，2020.

［23］KANG Z，PENG C，CHENG Q.Robust subspace clustering via smoothed rank approximation[J].IEEE Signal Proc Let，2015，22（11）：2088-2092.

［24］LIU J，MUSIALSKI P，WONKA P.Tensor completion for estimating missing values in visual data[J].IEEE Trans.Pattern Anal Mach Intell，2013，35（1）：208-220.

［25］JI T Y，HUANG T Z，ZHAO X L.A non-convex tensor rank approximation for tensor completion[J].Appl.Math.Model，2017，48：410-422.

责任编校：刘 燕，孙咏梅

A High Precision Low Rank Tensor Recovery Method Based on Balanced Tensor and Non-convex Function

SHI Chengfei，WANG Ming

（School of Aero Engine，Zhengzhou University of Aeronautics，Zhengzhou 450046，China）

Abstract：The classical low-rank tensor recovery method based on the minimization of the sum of the nuclear norms has been widely used in many fields.While，the results are not satisfactory in some specific scenarios，such as color video recovery，especially when the number of observations is small.One of the root causes lies in the unbalanced structure of the tensor，in which the dim sizes of some modes are much smaller than others，leading to extremely unbalanced and actually full or high rank unfolding matrices.Another reason should be attributed to the convex substitution of rank，and recent researches have demonstrated that some non-convex functions could approximate rank better than nuclear norm.To address the problem，this paper reconstructs a more balanced tensor through a reshaping operator，which retains the low rank property.Furthermore，a non-convex function is brought into tensor recovery as a better approximation of rank.Finally，experiments are carried out on color videos and the experimental results validate the effective of the method.

Key words：image processing；low rank tensor recovery；balanced tensor；logdet function

收稿日期：2024-01-21

基金项目：河南省重点研发与推广（科技攻关）专项（222102210113）

作者简介：石承飞，男，博士，硕士生导师，研究方向为信号处理、图像处理、低秩优化算法等。