基于马尔可夫链方法的股票价格预测研究

一、引言

改革开放以来，为了解决我国企业的融资问题，特别是国有企业股份制改革问题，我国建立了证券市场。1990年11月，上海证券交易所正式挂牌。随后，1991年4月，深圳证券交易所获中国人民银行批准。两家证券交易所的成立标志着新中国正式开启资本市场之门。我国证券市场经过30多年发展、壮大，至今已经形成包括主板、创业板、科创板、北交所在内的多层次资本市场体系。中国上市公司协会披露的2023年12月统计月报数据显示，截至2023年12月31日，境内股票市场共有上市公司5346家。其中，沪、深、北证券交易所分别有2263家、2844家和239家。在股份类型上，仅发行A股的公司有5113家，仅发行B股的公司有11家，而发行A+B、A+H等多股份类型的公司有222家。按控股类型划分，国有控股公司占26%，非国有控股公司占74%。行业分布上，制造业、信息传输、软件和信息技术服务业以及批发和零售业上市公司数量居前三名。与此同时，随着经济的发展，居民收入大幅提高，有了闲置的资金，投资意愿越来越强烈，股票投资已经成为很多人投资理财的重要渠道。在股票市场上，股票价格以及变化趋势是投资者盈亏的关键，预测股票价格变化成为众多投资者的“必修课”。

预测股票价格的方法有很多。一是基本面分析方法。该分析方法通过对影响公司内在价值的因素进行分析来预测其内在价值的变化，进而预测受价值驱动的股票价格未来的变化方向。二是趋势分析方法。该方法认为股票价格的变化是有趋势的，借助统计技术将股票价格变化生成各种模型，进而推断股票价格变化的趋势。这些模型包括各种自回归模型、移动自回归模型、差分自回归模型、GARCH模型等。三是随机过程分析方法。该方法认为股票市场是个复杂的非线性系统，股票价格受到各种因素的影响，既包括宏观、行业、公司经营等经济因素，也包括非经济因素，特别是交易者非理性等情绪因素，进而认为股票价格的运动是随机运动。而马尔可夫模型作为典型的随机过程分析方法，同时具备非因素与“无记忆性”等特点，因而也被运用到股票价格的预测中。

本文尝试采用马尔可夫模型预测股票价格的变化。以往该方法主要应用于个股股价预测，但在目前的市场环境下，个股特别是中小市值的股票价格经常受到人为操纵，采用马尔可夫模型预测的意义不大。本文聚焦沪深300指数，验证马尔可夫链预测法在短期内的预测效果，说明该方法的有效性。相较于既有文献，沪深300指数由沪深市场上市值规模最大的前300只股票组成，更具有预测意义。

二、马尔可夫链预测法的理论基础

马尔可夫（A.A.Markov）是俄国著名的数学家。二十世纪初，他在研究中发现，现实世界中有很多这样的随机现象，其变化过程与事物过去所处的状态无关，仅与事物的近期状态有关。后来的学者把具有这种特性的随机过程命名为马尔可夫过程。

（一）马尔可夫链内涵

1. 转移概率的定义。按照系统的发展，时间离散化为[n] =0，1，2，…。对每个[n]，系统的状态用随机变量[Xn]表示。设[Xn]可以取[k]个离散值[Xn]=1，2，…，[k]，且从初始状态开始，经过[n]步转移后，系统处于状态[i]的状态概率记为：

[ain=PXn=i] （1）

从[Xn]=[i]到[Xn+1]=[j]的转移概率记为：

[pij=P（Xn+1=j/Xn=i）] （2）

2. 马尔可夫链的定义。如果[Xn+1]的取值只取决于[Xn]的取值及转移概率[pij]，而与[Xn-1]，[Xn-2]…的取值无关，那么这种离散状态按照离散时间的随机转移过程称为马尔可夫链。

3. 马尔可夫链的特性。根据马尔可夫链的定义，马尔可夫链具有如下性质：

（1）马尔可夫性。马尔可夫性也称无后效性，即[Xn+1]的取值只与[Xn]和转移概率有关，与前期状态无关。

（2）平稳分布性。设马尔可夫链转移矩阵为[p]，则存在[π=（π1，π1…）]满足方程[π=πp] 且[jπj]=1，称[π=（π1，π2，…）]为该马尔可夫链的平稳分布。

（3）遍历性。马尔可夫链的遍历性是指无论系统现在处于哪个状态，从这个状态出发，经过足够长的一段时间，系统达到状态[j]的概率一定稳定在[η（j）]，[j=0，1，…]用数学极限公式表示为：[limx→∞pij=η（j）]。

（4）状态相通性。马尔可夫链的状态相通性是指系统无论从哪个状态出发，经过有限的转移次数，一定可以达到相同的状态。

4. 马尔可夫链的基本方程。由状态转移的马尔可夫性和全概率公式可以写出马尔可夫链的基本方程：

[ai（n+1）=j=1kaj（n）pji]，[i=1，2，…，k] （3）

并且[ai（n）]和[pij]应满足：

（1） [i=1kai（n）=1]， [n=0，1，2，…]；

（2） [pij≥0]， [i，j=1，2，…，k]；

（3） [j=1kpij=1]， [i=1，2，…，k] 。

记n步状态概率向量为[an=a1n，a2n，…，akn]，转移概率矩阵为：

[P=pij=p11…p1n⋮⋱⋮pn1…pnn] （4）

则基本方程的向量形式可表述为：

[a（n+1）=a（n）P] （5）

（二）马尔可夫链预测模型的建立

1. 模型假设。（1）过程的随机性。即系统从任意一种状态转移到另一种状态的过程是随机的。（2）过程的马尔可夫性。系统的转移概率只与当前的状态有关，与以前的状态无关。（3）转移概率矩阵保持稳定。即认为在一个有限的时间内，转移概率矩阵保持相对稳定。

2. 模型的建立。实际分析中，往往需要知道经过一段时间后市场趋势分析对象可能所处的状态，这就要求建立一个能反映变化规律的数学模型。马尔可夫市场趋势分析模型是利用概率建立一种随机性的时序模型，并用来进行市场趋势分析的方法。马尔可夫链的基本原理就是利用系统初始状态概率向量和转移概率矩阵来预测系统未来某一时期所处的状态。

设马尔可夫链的初始分布为：

[aj（0）] =[P（X0=aj）]，[aj∈I]，[j] =1，2，… （6）

其中，[I] =｛[a1]，[a2]…｝为马尔可夫链的状态空间。

初始状态转移向量为：

[a0=a10，a20，…，ak0] （7）

由马尔可夫链的基本方程的向量形式（5）得：

[a（n）=a（n-1）P=a（n-2）P2=…=a（0）Pn]

（8）

上式即为马尔可夫预测模型，其中P为概率转移矩阵。由模型可知，系统第[k]期的状态概率取决于系统的初始状态概率和转移概率矩阵的[k]次方。因此，如果已知系统初始状态概率向量[a（0）]以及转移概率矩阵[P]，则可以求得系统在任何一个时期处于任何一个状态的概率。

（三）马氏检验

设所研究的对象含有[k]个状态，用[Nij]表示在[X1，X2，…，Xn]中从状态[i]经过一步转移到状态[j]的频数，并将[Nijn×n]第[j]列之和除以各行各列的总和所得到的值记为边际概率[p·j]，即[p·j=i=1kNij/i=1kj=1kNij]，统计量[X2=2i=1kj=1kNij|logpijp.j|] 服从自由度为[（k-1）2]的[x2]分布。选定了置信度[α]，查表得[x2α（（k-1）2）]，若统计量[X2>x2α（（k-1）2）]，则认为[Xt]符合马尔可夫性，否则认为该过程不是马尔可夫链。

三、股票价格预测

本文以沪深300指数价格为例，在新浪财经网上搜集整理数据，通过马尔可夫链进行分析，预测价格走势。此次研究收集2024年2月19日—2024年4月19日的43个时间序列数据，进行每日收盘价格波动状态预测。

（一）基于马尔可夫链的股票每日收盘价格波动状态预测

1. 对价格时间序列数据分类。对股票每日收盘价格增长率进行分类处理，可将 43 组数据分为［-5%，-1%）、 ［-1%，-0.5%）、［-0.5%，0%）、［0%，0.5%）、［0.5%，1%）、［1%，5%）6 个状态空间，分别为S1、S2、S3、S4、S5、S6 ，如表1所示。

2. 建立股票每日收盘价格波动状态转移矩阵。根据表1得出价格增长率状态转移情况，如表2所示。

进一步可得状态转移频数矩阵[fij]和状态转移概率矩阵[pij]，如下所示：

[fij=010013003211141100121023111300201320]

[pij=01/5001/53/5003/72/71/71/71/74/71/71/7001/92/91/902/93/9dM1QYESaF+x8aCcmoXQ9yg==1/61/61/63/6002/801/83/82/80]

3. 马氏检验。由状态转移概率矩阵[pij] 得到边际概率值，如表3所示。进一步计算统计量[X2]，结果如表4所示。给定显著性水平 α＝0.05，查 [χ2] 分布表可得分位点[χ2α（（m-1）2）=χ2α]，由于[X2]=48.504>37.652， 因此，沪深300指数价格时间序列满足马尔可夫性。

4. 预测股票价格区间。先根据C-K 方程，求出 2-5 阶状态转移概率矩阵，然后通过各阶状态转移矩阵计算出相应的状态转移向量，进而预测沪深300指数价格增长率变化。

[P（2）=0.1830.0030.1940.3820.1790.0290.1530.3320.1350.1860.0990.0950.0360.1420.2810.1840.1420.2150.1360.1230.1900.3160.1370.0980.0790.2400.1510.0720.1680.2900.1010.2470.1010.1430.1330.275]

[P（3）=0.1070.2620.1180.1370.1340.2420.0800.1650.2110.2000.1430.2010.1380.2320.1720.2320.1220.1040.1100.2280.1500.1680.1400.2040.1300.1460.1970.2820.1390.1060.1210.1320.1930.2550.1560.143]

[P（4）=0.1150.1410.1970.2490.1500.1480.1260.2050.1720.2240.1340.1380.0970.1980.1830.1910.1380.1930.1150.1680.1870.2330.1430.1540.1090.2250.1580.1790.1360.1930.1180.2170.1560.1970.1360.176]

[P（5）=0.1180.2160.1600.1990.1350.1720.1060.1960.1770.2020.1390.1800.1190.1890.1800.2240.1380.1500.1150.2060.1680.2040.1370.1700.1140.1750.1850.2270.1420.1570.1110.1790.1820.2180.1430.167]

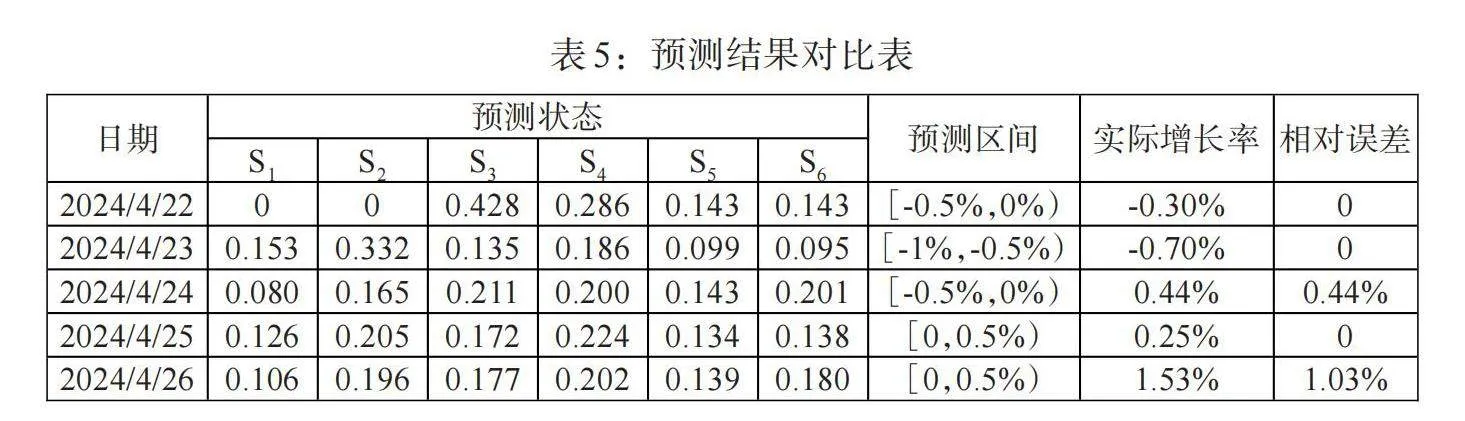
2024年4月19日，沪深300指数价格增长率为-0.79%，处于区间［-1%，0.5%），属于状态S2，初始状态向量定义为 [π（0）＝（0 0 1 0 0 0）]。则一步概率转移向量为 [π（1）＝π（0）＝（0 0 0.428 0.286 0.143 0.143）]，由此可以预测出下一个交易日2024 年4 月 22 日（4月20日、21日市场没有交易）的价格增长率处于状态 S3，预测概率为 42.8%，即对应的区间为［-0.5%，0%），实际增长率为-0.30%。

可由两步转移概率向量 [π（2）＝π（0）P（2）＝（0.153 ]

[0.332 0.135 0.186 0.099 0.095）] 预测出2024年4月23日的价格增长率所处的状态为S2，对应的状态区间为［-1%，-0.5%），实际增长率为-0.70%。

同理，可根据 [π3]、[π4]、[π5]预测出对应的状态区间，如表 5 所示。

（二）股票指数价格波动预测结果分析

沪深300指数价格波动预测结果表明，马尔可夫链对1—2天短期的价格波动率预测概率较高。随着预测日期的增加，预测结果与实际存在差异，并且预测概率降低。例如，根据三步转移概率向量预测，沪深300指数价格在2024 年 4 月 24 日的价格增长率属于状态 S3，预测区间为［-0.5%，0%）；实际增长率为0.44%，在［0，0.5%）区间中，属于S4状态。预测结果与实际增长率存在0.44%的相对误差，但属于相邻的两个状态，且预测概率S3的预测概率为21.1%，而真实增长率所属状态S4预测概率为20.0%，预测概率相差仅为1.1%，因此，预测结果有一定参考意义。

预测日期在5天的情况下，预测结果与实际误差较大，并且预测概率较低，且Fq5LNVxw30cuh67P6/l2hDv03hnXux9JUcyGh9V1kiY=有多个预测概率非常接近，预测基本无效。

四、结论与说明

本文选取我国沪深300指数2024年2月19日—2024年4月19日的43个时间序列数据，具有较强的代表性。从模型中可以得到：马尔可夫链对1—2天短期的价格波动率预测准确概率较高，随着预测日期的增加，预测结果与实际存在差异，并且预测概率降低。

对于这个结论，需要说明如下：第一，根据尤金·砝码的有效市场理论，在一个强式的有效股票市场，其大盘指数反映所有信息，股票价格是随机波动的，无法预测；但是，如果市场是弱式有效市场，可以通过分析过去的信息以及现在的信息，即采用传统技术分析以及基本分析方法预测大盘指数可能的走势；而市场如果是半强式有效市场，那么股票价格已经反映了过去的信息，基于历史数据分析的传统技术分析方法无效，只能通过现状分析来预测股票价格的变化，马尔可夫链就有了“用武之地”。因为马尔可夫链具有无后效性，即未来价格预测与过去特别是久远历史信息关系不大，而与现在以及刚刚过去的部分信息关系密切，可以通过计算状态转移概率来预测内部状态的变化，所以，马尔可夫链预测法只是一种概率预测方法，得到的预测结果仅仅表示大盘指数未来处于某种状态的概率，而非绝对会处于某种状态。第二，从预测结果看，我国股市经过多年的演化发展，效率得以提高，基本成为半强式有效市场。因此，基于技术分析的方法来预测股票价格是低效的，理性的投资者应该更多关注当前公司的基本面，进行价值投资。第三，股市大盘指数是受市场上的多种因素影响的结果，如市场多空双方的力量比较、宏观经济政策、行业景气度以及投资者的心理因素等，因而没有任何一种方法可以完全准确地预测出每天的大盘指数变化，马尔可夫链预测法也不例外。因此，可以把用马尔可夫链预测的结果和其他因素分析综合起来作为股票投资决策的判断依据。

（责任编辑 王 媛；校对 WY，LY）