基于完全自适应噪声集合经验模态分解的短时交通流组合预测

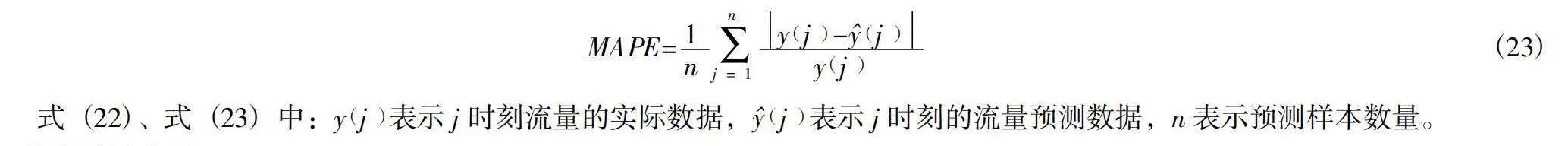
摘 要：为了提高短时交通流预测的准确性，鉴于短时交通流非平稳、难预测的特征，提出了基于完全自适应噪声集合经验模态分解（CEEMDAN）短时交通流组合预测方法。利用CEEMDAN将原始短时交通流信号进行分解得多个复杂度、频率不同的时间序列分量，利用排列熵算法（PE算法）计算各分量的复杂度；然后根据复杂度和随机性的不同分为高频和低频，分别使用ATT-TCN-BIGRU模型和ARIMA模型对高频分量和低频分量进行预测，最后叠加高频和低频的每个分量预测结果作为最终短时交通流预测值。仿真分析结果表明：与ARIMA模型、TCN模型、BIGRU模型、ATT-TCN-BIGRU模型相比，此模型的平均绝对误差及平均绝对百分比误差为最小，预测精度更高。

关键词：短时交通流预测；完全自适应噪声集合经验模态分解；排列熵；组合预测

中图分类号：F503 文献标志码：A

DOI：10.13714/j.cnki.1002-3100.2024.19.022

Abstract： In order to improve the accuracy of short-term traffic flow prediction， a short-term traffic flow combination predictiRRdl2+Lq3ZCtRCu/LEQt4A==on method based on Complementary Ensemble Empirical Mode Decomposition with Adaptive Noise（CEEMDAN）is proposed in view of the non-stationary and unpredictable characteristics of short-term traffic flow. CEEMDAN is used to decompose the original short-time traffic flow signal into multiple time series components with different complexity and frequency， and the complexity of each component is calculated by permutation entropy algorithm（PE algorithm）. Then， according to the complexity and randomness， it is divided into high frequency and low frequency， and the ATT-TCN-BIGRU model and ARIMA model are used to predict the high frequency component and low frequency component， and finally the prediction results of each component of high frequency and low frequency are superimposed as the final short-term traffic flow prediction value. The simulation results show that compared with the ARIMA model， TCN model， BIGRU model and ATT-TCN-BIGRU model， the average absolute error and average absolute percentage error of this model are the smallest， and the prediction accuracy is higher.

Key words： short-term traffic flow forecasting; complementary ensemble empirical mode decomposition with adaptive noise; permutation entropy; combined prediction

随着经济的发展和国家城市化的推进，机动车的保有量的激增给城市道路系统带来巨大压力，道路出现拥堵、通行能力下降等问题。智能交通系统根据实时交通信息，对交通流量进行疏导及控制，以减少出现道路拥堵的概率，从而达到缓解交通压力的目的。高效且精准的短时交通流预测是智能交通系统的重要组成部分，也是交通领域内研究的一个重点。

随着算法的更新，短时交通流的精度也在不断提高。近年来，国内外学者根据算法的优点并结合所需预测实际情况而选择合适智能算法组合进行预测，这样有效的提升了预测的准确性。张文胜等[1]引入改进的灰狼算法（TGWO）来优化BP神经网络建立模型；张玺君等[2]将季节性差分自回归滑动平均模型和Elman递归神经网络有效的融合，提出的一种基于SARIMA-GA-ELMAN的组合预测模型。胡松等[3]在使用最小二乘支持向量（LSSVM）的基础上引入改进后的算法对其进行优化建立ABOA-LSSVM预测模型，Liu et al.[4]将改进的LSTM与ARIMA结合构建SDLSTM-ARIMA模型，在改善算法不足的同时提升了预测的精度；Chai et al.[5]在将CNN与BIGRU结合的同时引入注意力机制构建CNN-BIGRU-ATT模型，多特征融合模型相较于基线模型有较好的预测效果。随着算法的发展，一些学者从非平稳性及非线性角度出发，降低交通流量时间序列非平稳性来提升预测效果，目前用于提高模型精度的时间序列分解方法很多。邴其春等[6]提出交通流经过经变分模态（VMD）分解后与长短时间记忆（LSTM）神经网络组合预测模型。马莹莹等[7]提出一种基于集合经验模态分解（EEMD）结合小波分析的短时交通流预测模型；Xiu et al.[8]为准确地捕捉其非线性和不稳定的趋势，提出了EEMD-BIGRU模型。EEMD分解中存在分解后残留白噪声的问题，CEEMDAN可以很好的解决这一问题，将CEEMDAN优点与其他算法有点相结合可以很好提升预测精度[9-11]；Rajalakshmi V et al.[12]将深度学习与ARIMA结合，提出一种新的混合短时交通流预测模型。上述模型中也考虑到分解后再预测思想，但是对分量特征考虑的不充分，因此如何建立适合分解后各个交通流时间分量特征的预测模型是在提升交通流预测精度方面仍需深入研究的问题。

为了提升短时交通流预测精度，本文提出了一种基于完全自适应噪声集合经验模态分解的短时交通流组合预测方法。首先采用完全自适应噪声集合经验模态分解（CEEMDAN）算法对原始交通流进行分解；然后使用排列熵算法对各分量进行复杂度检验并将其分为高频和低频，其中高频分量采用注意力机制-时间卷积网络-双向门控制循环单元（ATT-TCN-BIGRU）模型进行预测，低频采用自回归差分平移平均（ARIMA）模型进行预测。再后将各分量的预测结果进行叠加得到最终的预测结果。最后将此模型的预测结果与ARIMA模型、TCN模型、BIGRU模型及ATT-TCN-BIGRU模型预测结果进行比较。

1 理 论

1.1 CEEMDAN算法

完全自适应噪声集合经验模态分解（CEEMDAN）算法是从EMD算法和EEMD算法改进过来的，很好的解决了上述两种中模态混叠和分解后残留白噪声的问题，具有很好的分解完备性。CEEMDAN分解如下：

（1）将高斯白噪声βm加入到原始交通流信号Ym中，得到Ym=Ym+Tβm，其中T为噪声标准差。

（2）利用EMD对Ym进行I次分解得到CEEMDAN的IMF，并计算残余项rm。

IMF=IMFm （1）

rm=Ym-IMFm （2）

（3）对rm+TIMF

βm进行EMD信号分解得到CEEMDAN第2阶段的IMF和残余项rm。

rm=rm-IMFm （4）

（4）以此类推计算至l+1阶段，得第l阶段的残余项rm和第l+1个模态分量IMF。

（5）重复执行步骤（4）直到余量不能再分解。最终得到残余序列Rm和固有模态分解量IMF，原始信号Ym可表示为：

Ym=IMFm+Rm （7）

1.2 排列熵算法（PE算法）

PE算法可以量化时间序列中的不规则程度，是一种基于排列的信息熵度量方法，可用于研究时间序列复杂性和随机性。其原理如下：

给定时间序列yj， j=1，2，3，…， j=m， 其长度为m。

对时间序列进行重构，得相空间矩阵Y，如下：

Y= （8）

式（8）中：n为嵌入维度；t为时延。

对相空间矩阵Y中第k个向量Yk按升序重排，则有Yj+k-1t≤Yj+k-1t≤…≤Yj+k-1t。n维的有Y的排列方式n！种，经重排的Yk为n！种排列方式中的一种。在d1≤k≤n种排列方式中，其中一种排列方式的概率pd如下：

计算排列熵Hn的算式为：

1.3 时间卷积神经网路（TCN）

时间卷积网络（TCN）用来提取时间序列的高级特征，旨在捕获时间序列数据中的长期依赖关系，并在许多时间序列任务中取得了良好的性能。其构成部分分为因果卷积、膨胀卷积和残差模块。

因果卷积。TCN采用一维全卷积和因果卷积，可以保证网络输出长度和输入长度相同，且未来数据不会发生泄露。下面是因果卷积的定义序列Y=y，y，y，…，y，滤波器F=f，f，…，f，在y处的因果卷积为：

膨胀卷积。为了获取较长的时间序列，TCN采用膨胀卷积。下面是膨胀卷积的定义序列Y=y，y，y，…，y，滤波器F=f，f，…，f，在y处的膨胀因子为d的膨胀卷积为：

残差模块。因果卷积和膨胀卷积的引入会产生梯度消失或梯度爆炸问题，残差模块引入，将模型的输入y加权融合到模型的输入Fy中最终得到TCN的输出z，Activation为激活函数。

z=Activationy+Fy （13）

1.4 注意力机制

注意力机制（Attention Mechanism）是一种用于增强神经网络在处理序列数据或集合数据时的能力的技术。它在时间序列建模任务中广泛应用，并为模型提供了一种重要的机制，这种机制是模仿人类在看某处画面时注意力状态，在处理长序列时能够更好地关注重要信息并忽略不相关的部分[10]。本文注意力机制的原理：为TCN输出的值分配一个注意力权重，这些权重可以通过学习来自动确定，相乘后的结果作为BIGRU的输入，然后BIGRU模型可以选择性地关注不同的输入元素，实现对重要信息的集中处理，以提高预测的精度。

1.5 双向门控制循环单元（BIGRU）

门控循环单元（Gated Recurrent Unit， GRU）是在LSTM的基础上演化而来[13]，GRU能最大程度的减轻序列过长时存在的梯度爆炸或梯度消失问题，能很好的处理时间序列问题，对新样本有较强适应能力。GRU公式如下：

式（14）至式（17）中：t为时刻；y为更新门；r为重置门；w为权重矩阵；δ为sigmoid函数；h为输出值；*为哈达玛积。

BIGRU是由正向传播和反向传播的双向循环网络构成，这样同时考虑到数据前后变化规律，更好的发现数据的时序特征，结构如图1所示。

BIGRU公式如下：

式（18）至式（20）中：w为t时刻前向隐藏层的权重；为t时刻前向隐藏层的状态；w为t时刻后向隐藏层的权重；为t时刻后向隐藏层的状态；b为t时刻隐藏层状态的偏置；GRU为网络运算过程。

1.6  ARIMA算法

自回归差分平移平均模型（ARIMA模型）是由Ziegel和Jenkins提出来用于分析和预测时间序列数据的方法，它是一个适合预测线性平稳时间序列的回归模型，具有对线性捕捉能力强，设定简单的特点。ARIMA模型由三个部分组成：自回归（AR）模型、差分法（I）以及移动平均（MA）模型。AR模型表示前值和现值有怎样的关系，MA模型表示的是将自回归模型中误差项加和的结果；三者结合便可得到ARIMA模型。其表达式如下：

x=ux+ε+γε+b （21）

式（21）中：u表示自回归系数；γ表示移动平均系数；ε表示正态分布的误差项；x表示时间序列数据值；b表示常数；t是t时刻；p表示时序数据的滞后数，即（AR）项；q表示预测误差的滞后数，即（MA）项。

1.7 注意力机制-时间卷积网络-双向门控制循环单元模型（ATT-TCN-BIGRU模型）

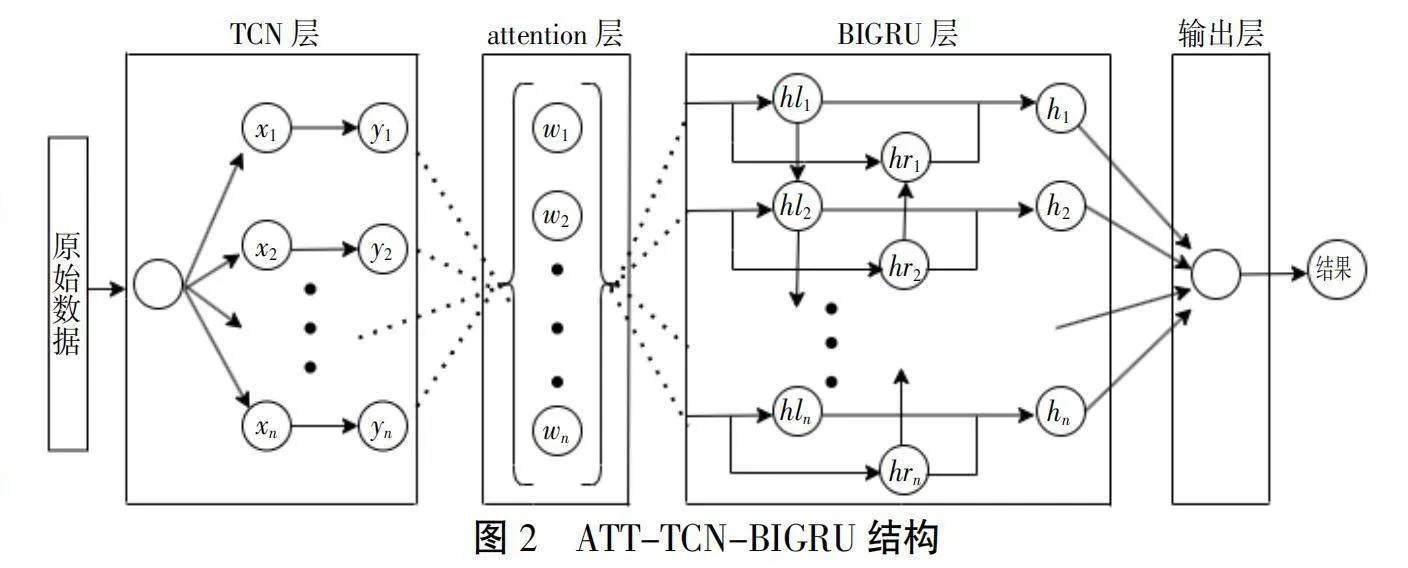
Nqt7PW9KG3dsmQZPmoXCEg== 时间卷积网络（TCN）是由卷积神经网络CNN变体而来，它可以直接使用卷积的特性来体现时间序列的高级持征，同时通过可扩张卷积结构捕获长期依赖关系，引入注意力机制，可以让模型更加关注TCN提取出的特征中的重要部分，然后根据上下文动态地分配不同特征的权重，同时模型也会根据数据的重要性进行自适应的特征加权。将TCN和注意力机制的结合可以使模型在不同的层级上对序列数据进行特征提取和加权处理，这样的多层级特征表示能够更全面地学习序列数据不同抽象层次的特征。BIGRU作为双向循环神经网络可以同时考虑过去和未来的上下文信息，这也使其可以更好地捕获序列中的全局结构。将三者结合起来使模型可以顾及过去和未来有效地掌握全局的结构，使模型更适合处理大规模和复杂的序列数据，以提高对序列数据的理解和建模能力，从而提高预测结果的精准度。ATT-TCN-BIGRU模型结构如图2所示。

2 基于完全自适应噪声集合经验模态分解的短时交通流组合预测模型

2.1 基于此模型的短时交通流预测

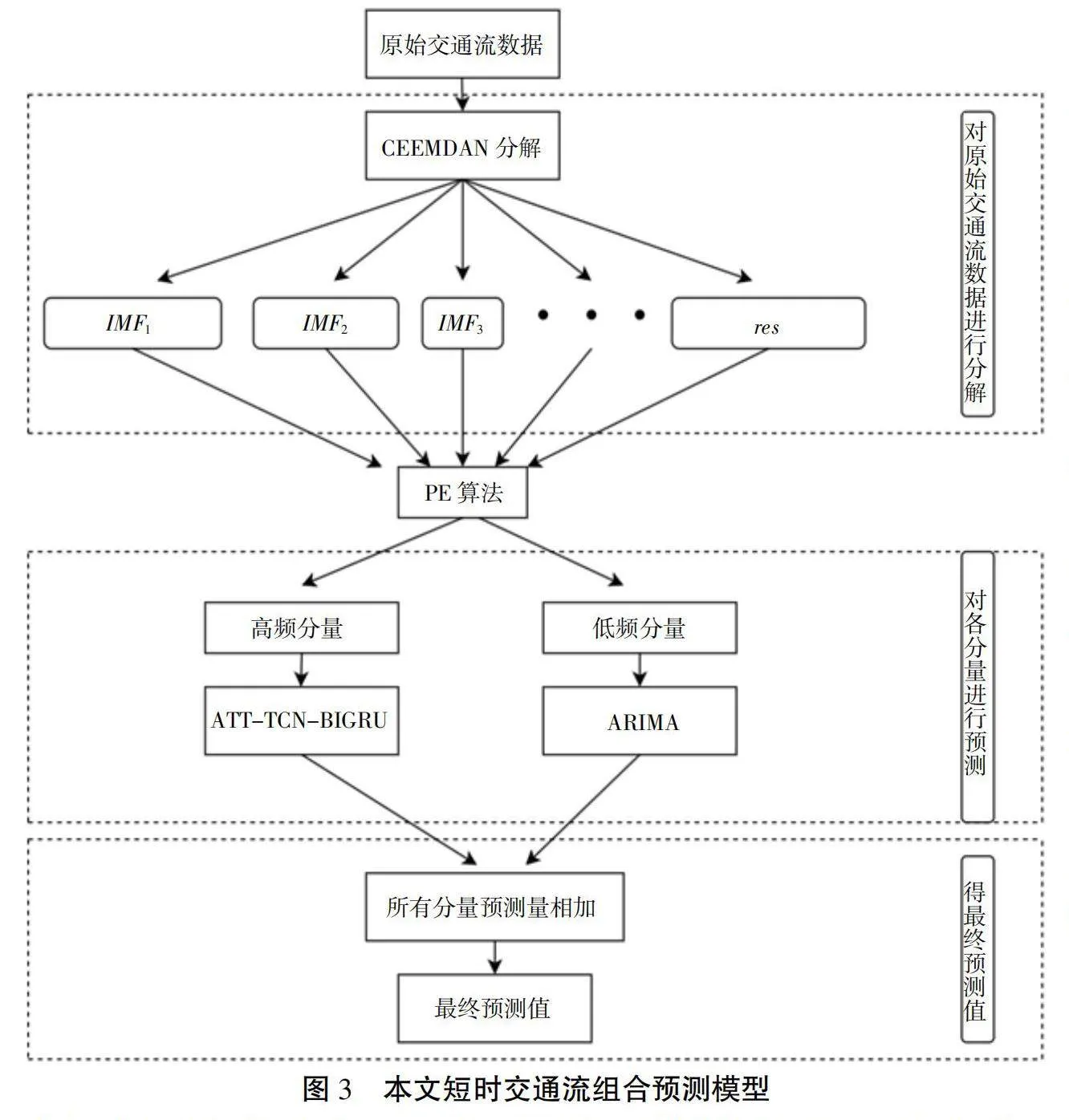
交通流预测领域中，短时交通流有非平稳、随机性高及难预测等特征，基于这些特征，本文提出了基于完全自适应噪声集合经验模态分解的短时交通流预测模型，此模型相比于单一的预测模型有更好的预测效果。CEEMDAN分解相加与EMD和EEMD可以将模态混叠和分解后残留白噪声的问题处理很好，分解的结果会更精准，本文使用CEEMDAN对原始交通流分解得到多个不同的分量，然后使用PE算法对各个分量进行随机性分析，将时间序列分量分为高频和低频。考虑到BIGRU算法可以通过在当前时刻同时考虑前后几个时间步的交通流量，且可以很好捕获序列中的全局结构，对非线性交通流有良好的预测效果，因此使用BIGRU对高频分量进行预测，为了提高预测效果，在BIGRU的基础上引入注意力机制和时间卷积网络（TCN），TCN可以直接使用卷积的特性来提现时间序列的高级持征，注意力机制可以根据上下文动态的TCN提取的特征分配不同特征的权重，以对不同特征进行不同的关注，使BIGRU算法捕捉特征时更有侧重点，建立ATT-TCN-BIGRU预测模型；考虑到自回归差分平移平均模型（ARIMA）可以很好的预测平稳的时间序列，使用ARIMA算法对低频分量进行预测。最后将每个分量的预测结果进行叠加，得到短时交通流最终预测值。基于完全自适应噪声集合经验模态分解的短时交通流预测模型流程图如图3所示。

基于完全自适应噪声集合经验模态分解的短时交通流组合预测模型步骤：（1）使用CEEMDAN对原始交通流时间序列进行分解，得到m个IMF分量；（2）使用排列熵（PE）算法对IMF分量进行随机分析，并计算每个IMF分量的排列熵值，将分量分为高频分量和低频分量；（3）使用ATT-TCN-BIGRU模型对非平稳且随机性高的高频IMF分量进行预测，使用ARIMA模型对稳定且随机性低的低频IMF分量进行预测；（4）将每个IMF分量的预测结果进行叠加，得到最终短时交通流预测值。

2.2 评价指标

预测评价指标是一种度量预测模型准确性的标准化方式，可以用来分析对比预测效果，通过评估模型的准确性来比较模型预测效果。均方根误差RMSE衡量的是预测值与实际值之间的误差大小；平均百分比误差MAPE是预测误差的绝对值占实际值的百分比的平均值，能够量化预测值相对于实际值的百分比误差，二者皆是之前越小预测效果越好，本文使用这两指标作为评价标准。评价指标公式如下：

RMSE= （22）

MAPE= （23）

式（22）、式（23）中：yj表示j时刻流量的实际数据，j表示j时刻的流量预测数据，n表示预测样本数量。

3 仿真结果分析

3.1 数据筛选

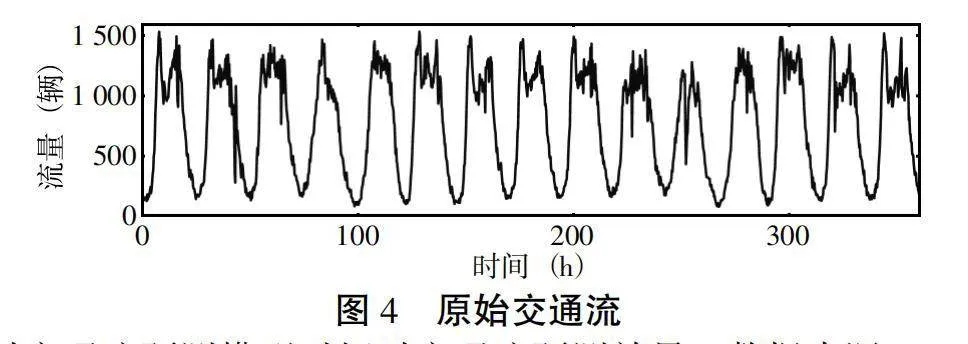
道路交通流之所以会呈现出非线性和不确定性的特征，是因为道路上存在很多影响交通的因素，如：突发状况、恶劣天气、道路施工、信号灯配时等因素。即使有很多影响因素，但是绘出原始交通流的图后发现还是呈现一定规律的，以15min为间隔的原始数据曲线图如图4所示。为了验证基于完全自适应噪声集合经验模态分解的短时交通流预测模型对短时交通流预测效果，数据来源于PeMS系统2019年8月1日—2019年8月15日，15天以15min为时间单位采样的数据结果。

先对原始交通流数据进行处理，最后得到1 440个数据。将处理好的数据输入建立好的模型中。用前面的交通流数据作为训练集来预测最后一天交通流数据。将前面14天的1 344个数据作为模型训练集来输入，最后一天的96个数据作为验证集输出。

3.2 基于CEEMDAN算法的分解

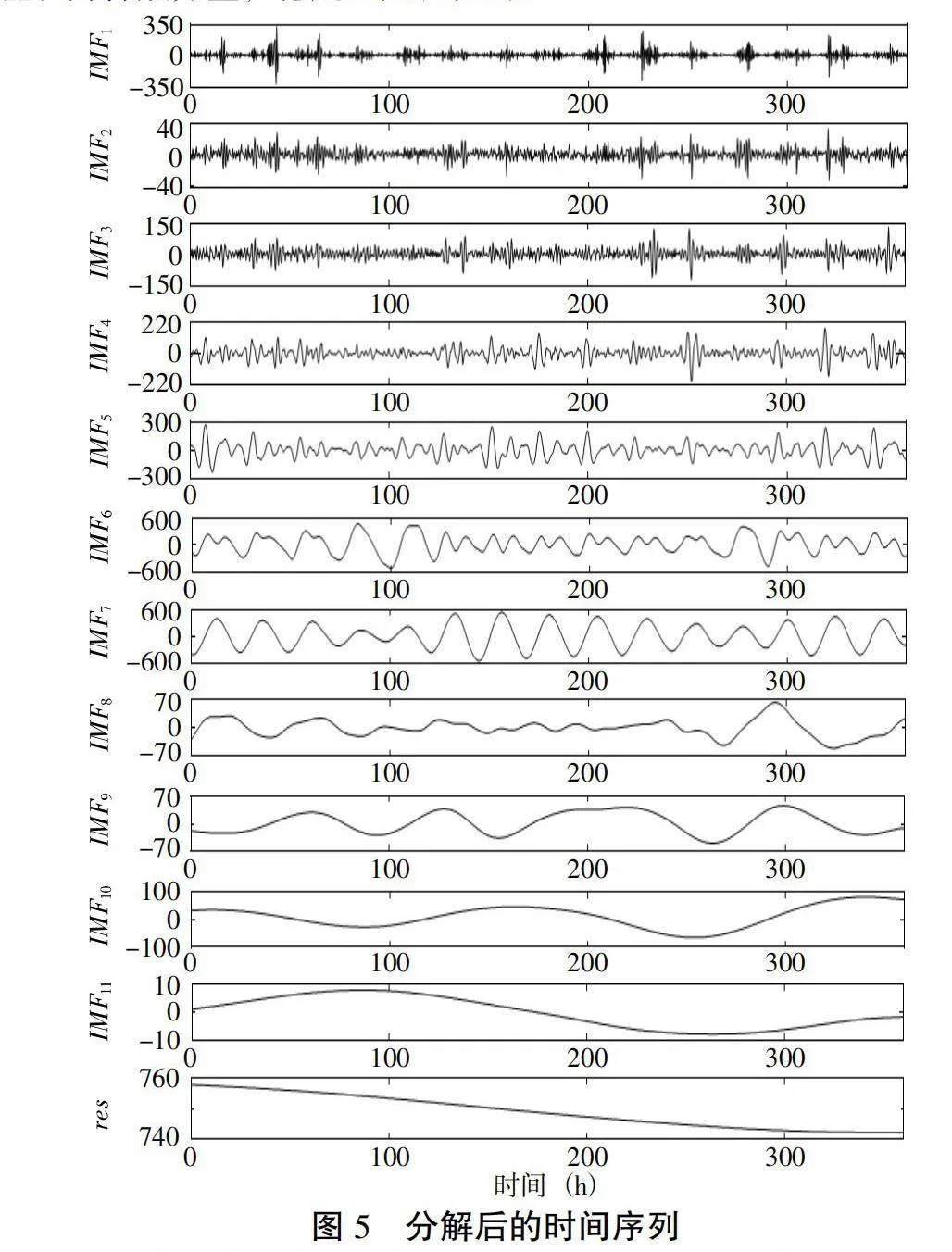
基于Python软件，使用CEEMDAN算法对处理后的数据进行分解，将参数设置为：加入高斯白噪声的组数为100，高斯白噪声的标准差为0.2，迭代次数为500。则处理后的数据经CEEMDAN的分解得到12个平稳性和随机性不同的IMF分量。经CEEMDAN分解后的各个序列图像如图5所示。

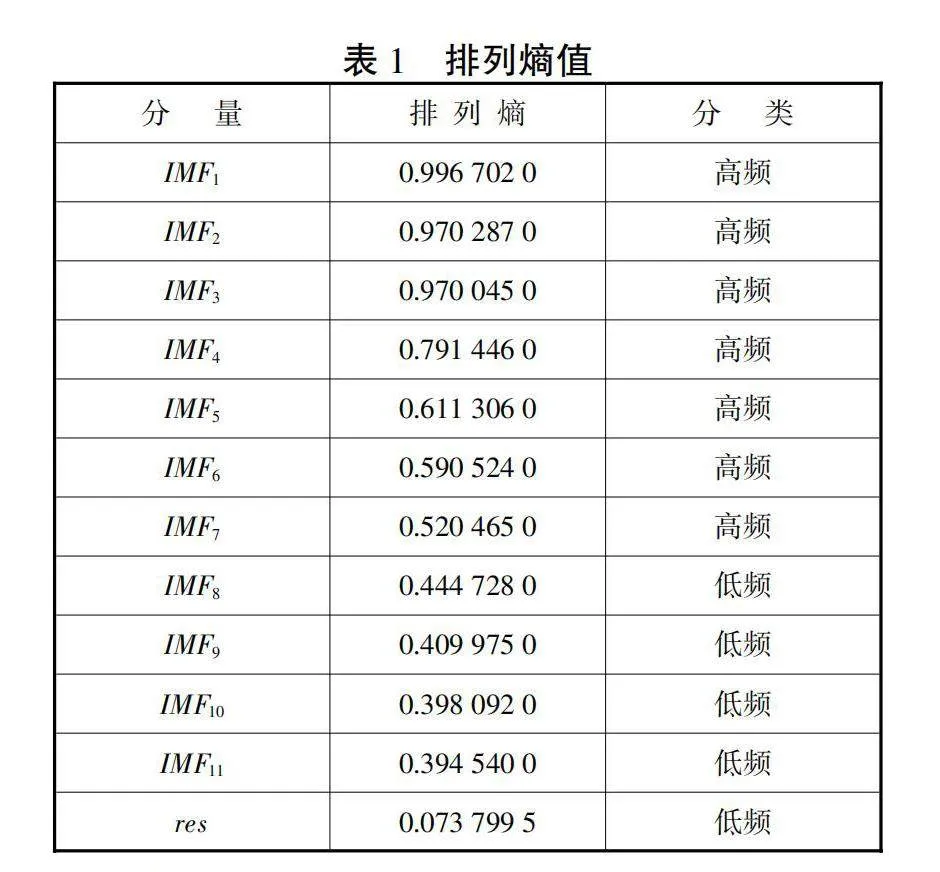
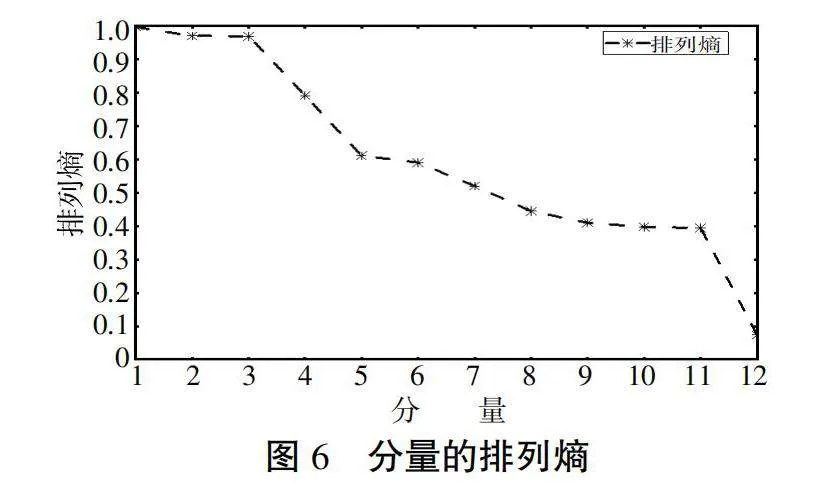
为了提高运算效率，基于Python计算得到各个IMF分量的排列熵值，参数设置为：嵌入维数为6，延迟时间为3。各IMF分量的排列熵值如表1所示，排列熵值趋势如图6所示。将排列熵值大于等于0.5的IMF分量看作高频分量，排列熵值小于0.5的IMF分量看作低频分量[14]。从表1和图6中可以看出IMF1—IMF7为高频分量，不稳定且随机性强；IMF8—IMF11及res残差项为低频分量，稳定且随机性弱。

3.3 ; 基于完全自适应噪声集合经验模态分解的短时交通流预测

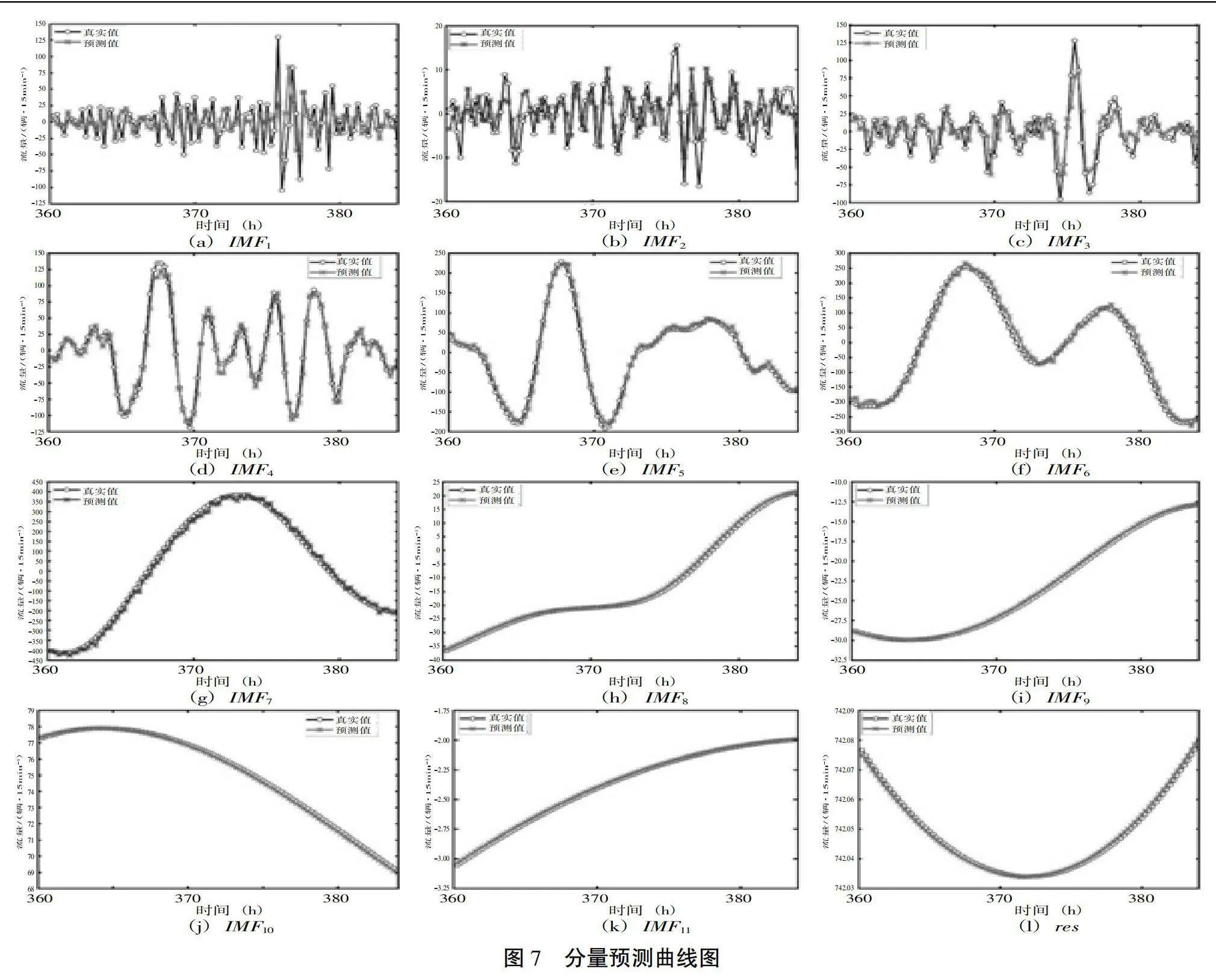
鉴于高频分量和低频分量的特点不同，分别建立ATT-TCN-BIGRU预测模型和ARIMA预测模型。对于高频分量IMF1

—IMF7，使用ATT-TCN-BIGRU模型进行预测；对于低频分量IMF8—IMF11及res残差项，使用ARIMA模型进行预测。各分量预测值与真实值对比结果如图7所示。

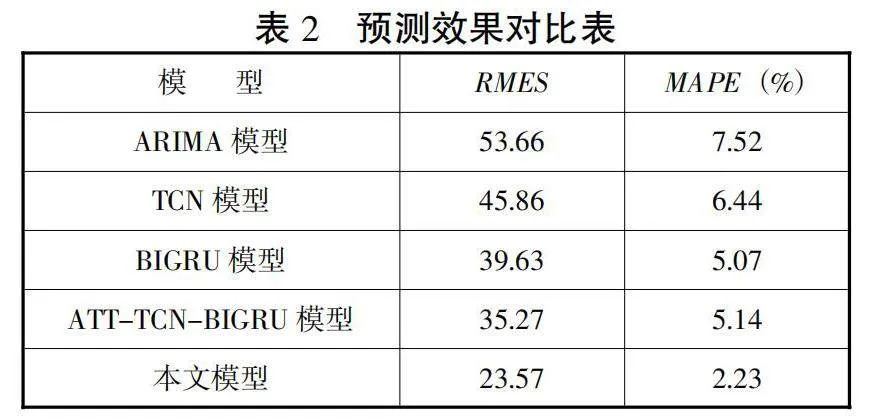
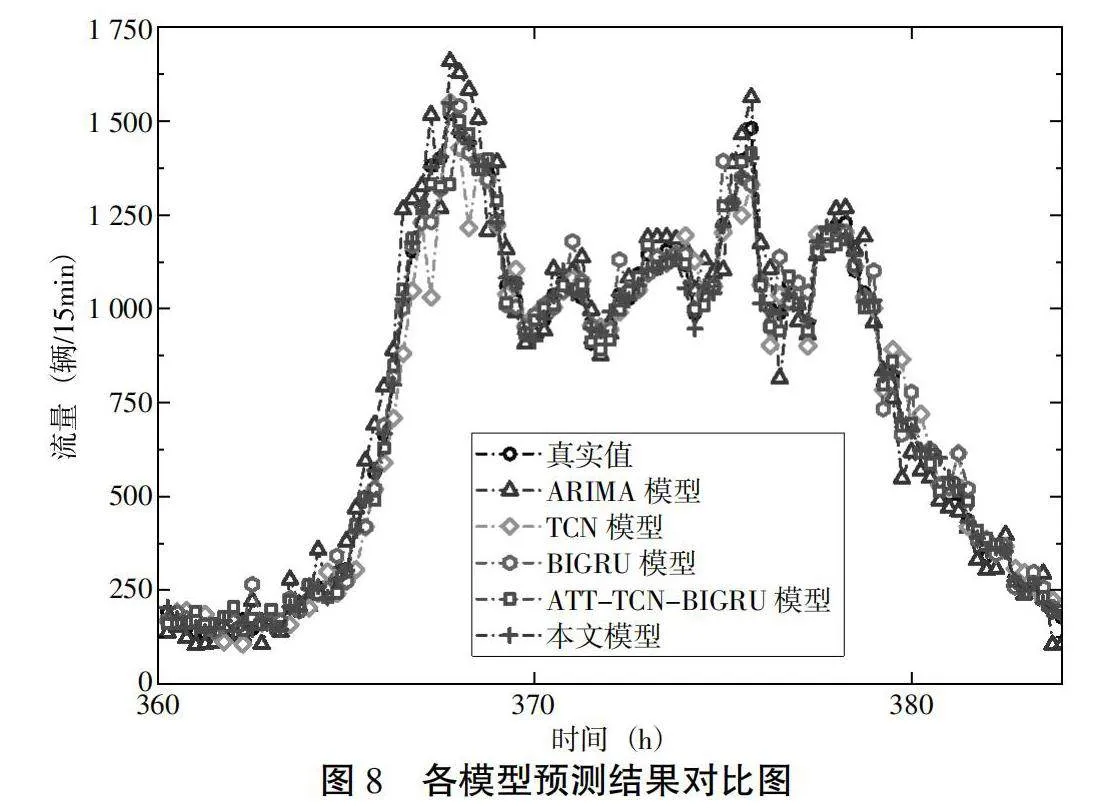
为了验证本组合模型对短时交通流预测效果，将ARIMA模型、TCN模型、BIGRU模型、ATT-TCN-BIGRU模型与本模型的预测结果进行对比，如图8所示。本文模型与其他模型的性能结果对比如表2所示。

从表2中的结果评价指标可以看出，相比于其他几个模型，本文提出的组合模型的预测值与真实值的拟合效果最好。从表2中可以得出，ARIMA模型的拟合效果最差，这是因为短时交通流随机性较高，ARIMA模型一般适用于平稳的时间序列；TCN模型和BIGRU模型的预测值对真实值的拟合效果相比于ARIMA模型呈现出变好的趋势；相较于单一预测模型，组合预测的效果更好，ATT-TCN-BIGRU模型预测值对真实值的拟合效果优于前面几种单一的模型，而相比于本文提出的组合预测模型，拟合效果依然不是很优。本文的组合模型原始交通流用CEEMDAN进行分解，然后不同特性的分量选择与其适合的预测模型，最后预测效果较其他模型好些。因此，基于完全自适应噪声集合经验模态分解的短时交通流预测模型提升了预测的精度，有很好的预测效果。

4 结 论

为了提高预测的准确性，针对具有非平稳、随机性高及难预测等特性的短时交通流，本文提出了基于完全自适应噪声集合经验模态分解的短时交通流预测模型。首先，对预处理后的原始交通流使用CEEMDAN进行分解，然后使用排列熵（PE）算法对分解后的各分量进行平稳性和随机性的分析，并将其分为高频分量和低频分量。之后，针对不同特性的分量选择合适预测模型进行预测。最后将各分量的预测结果进行叠加，得到最终的预测结果。将本文模型与其他模型预测结果进行对比，结果表明，预测效果在一定程度上有所提高。当然，本文模型所考虑的对象较少，后期可以考虑多路段问题及更复杂的时空问题，使研究更贴近于实际问题，从而提升交通流预测在交通决策中的可靠性。

参考文献：

[1] 张文胜，郝孜奇，朱冀军，等. 基于改进灰狼算法优化BP神经网络的短时交通流预测模型[J]. 交通运输系统工程与信息，2020，20（2）：196-203.

[2] 张玺君，王晨辉. 基于SARIMA-GA-Elman组合模型的短时交通流预测方法[J]. 兰州理工大学学报，2022，48（5）：107-113.

[3] 胡松，成卫，李艾. 一种改进鲸鱼算法及其在短时交通流预测中的应用研究[J]. 小型微型计算机系统，2021，42（8）：1627-1632.

[4] LIU B， TANG X， CHENG J， et al. Traffic flow combination forecasting method based on improved LSTM and ARIMA[J]. International Journal of Embedded Systems， 2020，12（1）：22-30.

[5] CHAI C， REN C， YIN C， et al. A multifeature fusion short-term traffic flow prediction model based on deep learnings[J]. Journal of Advanced Transportation， 2022，2022：1702766.

[6] 邴其春，张伟健，沈富鑫，等. 基于变分模态分解和LSTM的短时交通流预测[J]. 重庆理工大学学报（自然科学），2023，37（5）：169-177.

[7] 马莹莹，靳雪振. 基于EEMD和小波阈值的短时交通流预测研究[J]. 重庆交通大学学报（自然科学版），2022，41（6）：22-29.

[8] XIU C， SUN Y， PENG Q， et al. Learn traffic as a signal： Using ensemble empirical mode decomposition to enhance short-term passenger flow prediction in metro systems[J]. Journal of Rail Transport Planning & Management， 2022，22：100311.

[9] 聂铃，张剑，胡茂政. 基于CEEMDAN分解的短时交通流组合预测[J]. 计算机工程与应用，2022，58（11）：279-286.

[10] GAO H， JIA H， YANG L. An improved CEEMDAN-FE-TCN model for highway traffic flow prediction[J]. Journal of Advanced Transportation， 2022（6）：1-20.

[11] ZHU Y， ZHANG K， ZHAO C. Short-term traffic flow prediction of expressway based on CEE-MDAN-PE-BiGRU combined model optimized by attention mechanism[C] // 2022 International Conference on Big Data， Information and Computer Network（BDICN）. IEEE， 2022：80-87.

[12] RAJALAKSHMI V， GANESH VAIDYANATHAN S. Hyb-rid time-series forecasting models for traffic flow prediction[J]. Promet-traffic & Transportation， 2022，34（4）：537-549.

[13] A MIGLANI， N KUMAR. Deep learning models for trafic flow prediction in autonomous vehi-cles： A review， solutions， and challenges[J]. Veh Commun， 2019，20：100184.

[14] 王飞，孙鹏飞. 基于分解集成方法的空中交通流量短期预测[J]. 科学技术与工程，2021，21（35）：15270-15276.