低碳车辆路径问题及求解算法研究综述

摘 要：随着绿色物流的兴起，低碳车辆路径问题（Low-carbon Vehicle Routing Problem， LCVRP）成为了物流领域研究的焦点，对LCVRP最新研究文献及进展进行综述。首先，对影响车辆油耗和碳排放的主要因素进行分析归纳，总结常用的油耗和碳排放测度模型；其次，对求解LCVRP及其变体问题的精确算法、经典启发式算法、元启发式算法进行较为详细的综述；最后，针对LCVRP现有的研究不足指出未来待发展方向。

关键词：低碳车辆路径问题；油耗；启发式算法

中图分类号：U116.2 文献标志码：A

DOI：10.13714/j.cnki.1002-3100.2024.19.020

Abstract： With the rise of green logistics， Low-carbon Vehicle Routing Problem（LCVRP）has become the focus of research in the field of logistics. This paper is intended to review the latest research literature and progress of LCVRP. Firstly， the main factors affecting vehicle fuel consumption and carbon emissions are analyzed， and the commonly used measurement models of fuel consumption and carbon emissions are summarized. Secondly， the precise algorithms， classical heuristic algorithms and meta-heuristic algorithms for solving LCVRP and its variants are reviewed in detail. Finally， the future development direction of LCVRP is pointed out in view of the lack of existing research.

Key words： low-carbon vehicle routing problem; fuel consumption; heuristic algorithm

0 引 言

随着环保理念的不断普及以及对经济高质量发展的转型需求，低能耗、低排放、低污染的低碳经济发展理念被提出，得到了学术界和政府部门的广泛关注。物流业是推动国民经济发展的基础性、支柱性产业，是低碳经济的重要组成部分，而在物流业减排行动中，由于交通运输业以公路货车运输为主的特性，能耗和碳排放量更大，物流运输成本更高，从而成为了国家环保攻坚、节能减排的重点改进领域。因此，研究低碳化物流运作具有一定现实意义和理论价值。

车辆路径问题（Vehicle Routing Problem， VRP）是交通运输优化和运筹学领域中的重点研究方向之一，是物流配送领域中的热点问题。最早由Dantzing et al.[1]提出，其主要研究内容为：存在一个配送中心与若干个客户点，已知其地理位置和客户需求量，在不违反约束的条件下规划恰当的服务顺序以达到配送成本最小的目的。随着应用场景的不断拓宽，经典的VRP已不能应对复杂多变情形的要求，出现了诸多VRP变体类型，如带时间窗的VRP（VRP with Time Windows， VRPTW）、低碳VRP（Low-carbon VRP， LCVRP）、同时取送货的VRP（VRP with Simultaneous Pickup and Delivery， VRPPD）等，不同的约束条件和影响要素组合成了不同的变体问题。LCVRP在经典的VRP上加入了碳排放约束，在考虑经济效益的前提下，旨在科学的规划行车路线以降低配送过程中的燃油消耗和碳排放，由于影响车辆碳排放的因素众多且因素之间参差交错，LCVRP的模型更为复杂，求解难度更大。为顺应物流绿色低碳发展要求，学者们对LCVRP展开了一系列研究，具体集中在两个方面：一是对影响车辆碳排放的因素进行研究；二是碳排放计量方法。本文通过对国内外相关文献进行梳理和总结，先对LCVRP的研究进展进行综述，再对求解此类问题最具代表性的算法进行分析和讨论，最后结合现有文献，展望LCVRP未来的研究趋势。

1 LCVRP研究进展

1.1 油耗和碳排放影响因素

车辆作为分布最广的移动碳排放源，产生的碳排放量达交通运输排放总量的80%以上，重型卡车更是污染重灾区。如何确定车辆油耗和碳排放的关键影响因素以便有效规划配送路径成为了LCVRP关注的焦点。学者们对影响燃油消耗的因素进行了一系列研究，大致可以分为与外部环境有关的天气、交通状况，涉及人为主观因素的驾驶员经验以及车辆自身参数等几类[2-3]。通过总结整理相关文献，本文以油耗影响相关度高的行驶速度为依据，将其分为以下五类：

（1）车辆参数。主要包括与车辆外观有关的车辆大小、重量、类型与形状，与车辆性能有关的发动机尺寸、燃油类型等。尤其是车型与负载在实际配送活动中容易测度与统一，因而有较多学者研究不同车辆类型[4]，如轻型、中型、重型车辆，以及车辆在不同节点完成配送后货物卸载情况对油耗和碳排放的影响[5]。

（2）交通状况。道路交通流量、行驶速度和加速度对燃油消耗和碳排放有直接影响。卢笙等[6]研究车辆平均速度与实际道路油耗的关系，发现油耗在30km/h以下时，会随速度降低而显著上升。但随着当代城市交通拥堵愈加严重，车辆行驶速度普遍降低，偏离最佳行驶速度又会导致油耗和碳排放增加[7]，因而考虑交通拥堵的时变VRP研究[8]更能满足实际需要，设计高效的拥堵规避方案有助于物流碳减排。

（3）环境因素。环境对碳排放的影响主要表现在道路坡度、路面类型以及温度、风阻和海拔等自然条件方面。随着道路坡度的升高，车辆为克服阻力需要做额外功，油耗和碳排放也随之升高。尤其是碳排放因子对坡度更为敏感，影响排序为道路坡度>车辆类型>道路类型[9]。而在城市物流配送中，随着道路等级越高，道路承载的交通量变大，相应的碳排放量也越高。同时，海拔和温度的升高也在一定程度上增加了高油耗的概率[10]。

（4）驾驶员行驶习惯。驾驶员技术水平、行车习惯等显著影响油耗和碳排放，经验丰富且行车激进的驾驶员所消耗的燃油量通常更高。男性驾驶员碳排放量也往往高于女性驾驶员[11]。Loman et al.[12]对三种不同的驾驶风格进行测试，速度最高的动态驾驶风格往往伴随着高油耗。

（5）运营管理。运营管理主要体现在车辆组合、调度等管理层面。现代居民需求多样，配送商品种类更为繁杂，单车型配送难以满足实际需要，因此考虑多车型组合的异构VRP十分必要。Cheng et al.[13]测试了同质车队和异构车队对碳排放的影响，表明使用异构车队时的碳排放成本更少。邱玉琢等[14]进一步讨论了租赁车队和自有车队的经济性，证实考虑外部车队对降低碳排放成本有效。

1.2 油耗和碳排放测度模型

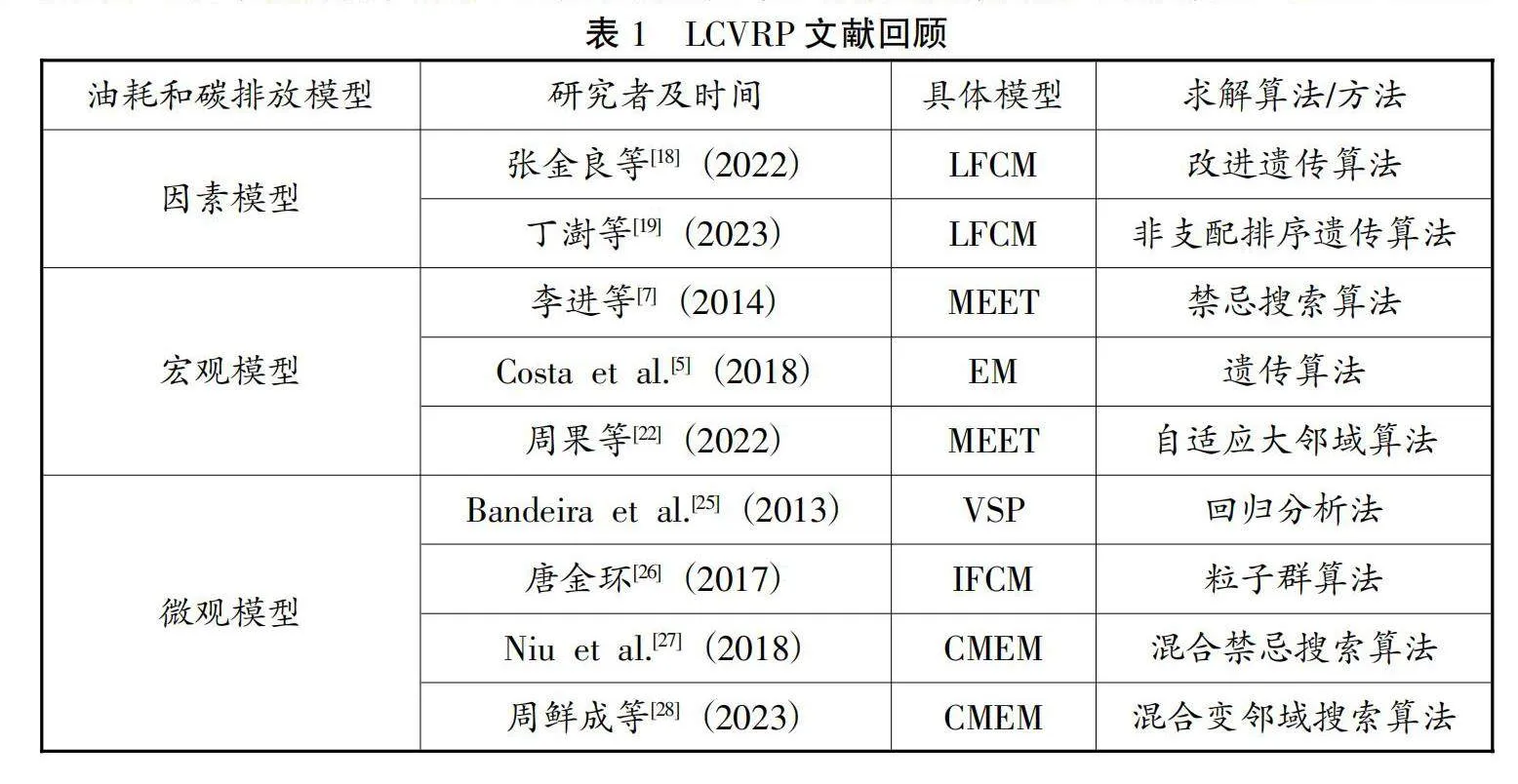
影响车辆碳排放的因素众多，如何量化排放因子以建立适用不同场景的油耗和碳排放模型是LCVRP研究的基础。目前应用最广泛的油耗和碳排放模型可分为三类：（1）因素模型，早期研究对油耗的估算所考虑的影响因素较为简单，通常将车辆油耗简化成与载重、行驶距离等有关的线性函数。Xiao et al.[15]提出了基于载重的油耗模型（Load Based Fuel Consumption Model， LFCM）。Mohammadi et al.[16]在对碳排放和油耗的刻画中，仅考虑了距离因素。吴丽荣等[17]构建了基于速度和负载的油耗测度模型。由于LFCM模型易于量化，因此学者们多用来简单测算油耗[18-19]。（2）宏观模型，主要使用参数平均值或构造回归函数来估算整个区域的碳排放。在VRP领域应用较多的有Hickman et al.[20]提出的考虑车辆平均速度、载重和道路坡度的碳排放测度模型（Methodology for Calculating Transportation Emissions and Energy Consumption， MEET）和Kouridis et al.[21]提出的考虑速度和行驶距离的碳排放计量模型（Computer Programme to Calculate Emissions from Road Transportation，COPERT）。周果等[22]分别采用了LFCM模型、MEET模型估算油耗和碳排放。（3）微观模型，以更全面的参数，如加速度、发动机效率、动态速度等来估算油耗。Bowyer et al.[23]提出了考虑车辆行驶牵引力、速度和加速度等多种微观因素的瞬时油耗模型（Instantaneous Fuel Consumption Model， IFCM），用于近似计算车辆每秒的油耗量。Barth et al.[24]在IFCM模型基础上，加入了发动机功率和转速等相关参数，提出了综合排放模型（Comprehensive Modal Emission Model， CMEM）。微观模型考虑因素更多，对碳排放预测更为精确，因而在物流配送领域应用更多[25-28]。上述三类油耗模型在LCVRP领域均得到了一定的应用，相关研究成果归纳如表1所示。

2 LCVRP求解算法

LCVRP属于NP-hard问题，求解难度会随着模型约束增多而增大，难以在短时间内求得最优解或近似最优解。目前，国内外学者求解该类多复杂约束VRP[22]的算法主要有精确算法、经典启发式算法和元启发式算法。

2.1 精确算法

精确算法是指在组合优化问题中能够求得绝对最优解的传统算法，其计算复杂度会随问题规模的增大呈指数增长，因而只适应于小规模算例的求解。用于求解LCVRP的精确算法主要有：分支界定法[8]、动态规划法[29]、割平面法[30]和整数线性规划法[31]。精确算法通常用来改进解的上界和下界，与启发式算法结合进行优化求解。

2.2 经典启发式算法

启发式算法是基于直观或者经验构造的算法，在满足相应约束下给出问题的可行解，包括经典启发式算法和元启发式算法。经典启发式算法通过逐步构造路径来形成可行解，通常被用来求解大规模的VRP以及为元启发式算法提供较高质量初始解[31-32]。穆东等[31]采用了前向插入算法构造初始解。Niu et al.[27]和Pu et al.[32]在求解LCVRP时，分别提出使用最近邻法、贪心算法来求得高质量的初始解。

2.3 元启发式算法

元启发式算法通过对邻域解进行不断地扰动和变换操作，尽可能使得算法搜寻到整个搜索空间，从而无限接近最优解。其求解性能优于经典启发式算法，常被用来求解带复杂约束的LCVRP及其变体问题[24]。在实际的应用中，单一的元启发式算法有其局限性，而混合多种局部搜索算子[23]、算法策略优化[33]等的改进元启发式算法适应性更强，求解表现更优。

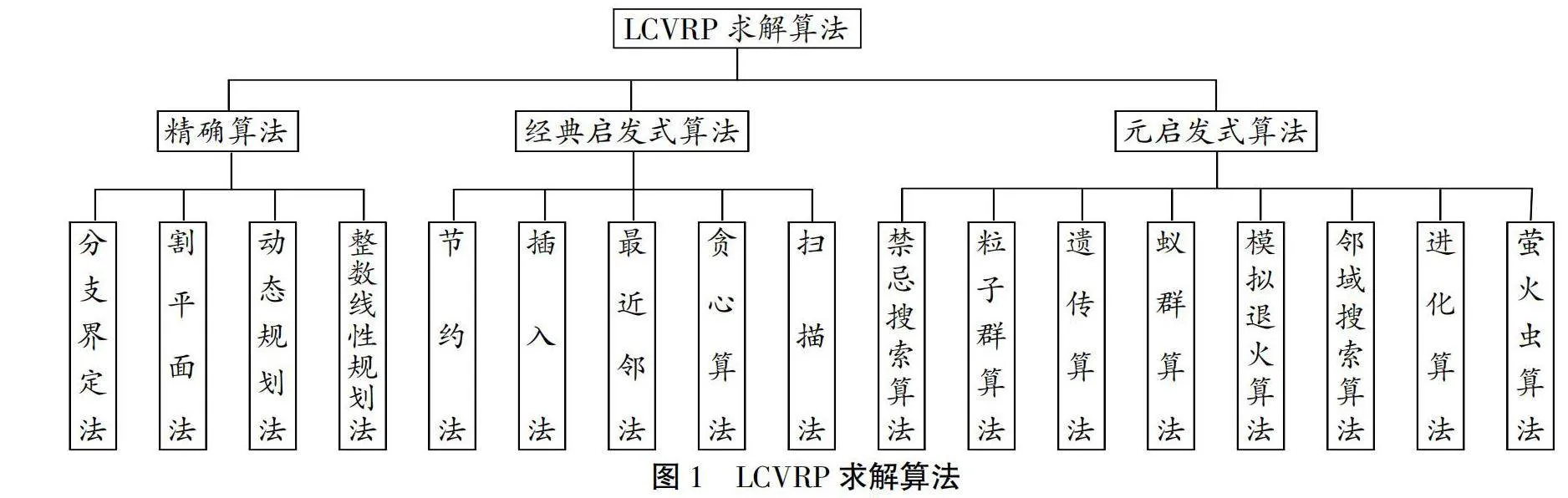
为进一步提高算法的搜索性能和收敛速度，学者们对多种启发式算法进行组合优化使用。常见的算法组合策略有：（1）两种或多种呈并行关系的启发式算法混合，如两阶段混合启发式算法[34]，第一阶段使用启发式算法构造初始解或进行全局遍历搜索，第二阶段使用其他算法进行局部搜索，平衡算法的全局搜索和局部搜索能力。（2）两种或多种启发式算法完全混合，一般以某种启发式算法为主算法，结合其他启发式算法的个别搜索策略以提高算法的寻优能力[28]。混合启发式算法在求解复杂LCVRP上具有一定的优越性如图1所示。

3 总结与展望

LCVRP是在碳排放的约束下涉及行驶速度、环境、交通状况等复杂路径规划问题，以整体运输碳减排为目标，优化配送路线从而实现总物流成本的降低，具有广阔的应用前景与研究价值。近几年针对LCVRP及其求解研究众多，取得了丰富的研究成果，但仍存在急待解决问题：（1）现有的油耗和碳排放测度模型较少考虑会驾驶员主观因素、实时交通状态等对碳排放的影响，适用范围有一定的局限。（2）碳排放量的转换常用油耗乘以某个固定转换系数，但实际中不同类型、大小的车辆油耗受多重因素影响表现出较大差异，进而碳排放量的计算也出现偏差。因此，在碳排放测度中考虑车辆参数、实时速度、突发状况等动态影响因子十分必要。（3）新能源车因其能耗小、无污染在物流配送领域应用广泛，但由于电池容量、充电限制，导致搭载货物、配送范围局限大，因此与燃油车辆共同组合配送研究成为了未来LCVRP的研究方向之一。

参考文献：

[1] DANTZIG G B， RAMSER J H. The truck dispatching problem[J]. Management Science， 1959，6（1）：80-91.

[2] ARDEKANI S， HAUER E， JAMEI B. Traffic impact models[J]. Traffic Flow Theory， 1996，7（1）：1-26.

[3] BIGAZZI A Y， BERTINI R L. Adding green performance metrics to a transportation data archive[J]. Transportation Research Record， 2009，2121（1）：30-40.

[4] DEMIR E， BEKTAS T， LAPORTE G. A comparative analysis of several vehicle emission models for road freight transportation[J]. Transportation Research Part D： Transport and Environment， 2011，16（5）：347-357.

[5] DA COSTA P R O， MAUCERI S， CARROLL P， et al. A genetic algorithm for a green vehicle routing problem[J]. Electronic Notes in Discrete Mathematics， 2018，64：65-74.

[6] 卢笙，吴烨，张少君，等. 基于车载诊断系统的轻型乘用车实际道路油耗特征分析[J]. 环境科学学报，2018，38（5）：1783-1790.

[7] 李进，张江华. 基于碳排放与速度优化的带时间窗车辆路径问题[J]. 系统工程理论与实践，2014，34（12）：3063-3072.

[8] LUO H， DRIDI M， GRUNDER O. A branch-price-and-cut algorithm for a time-dependent green vehicle routing problem with the consideration of traffic congestion[J]. Computers & Industrial Engineering， 2023，177：109093.

[9] 周涛，李毅军，孙琴梅，等. 大数据驱动下的山地城市道路条件对车辆碳排放影响研究[J]. 交通运输系统工程与信息，2023（5）：172-183.

[10] GONG J， SHANG J， LI L， et al. A comparative study on fuel consumption prediction methods of heavy-duty diesel trucks considering 21 influencing factors[J]. Energies， 2021，14（23）：8106.

[11] KHADER A I， MARTIN R S. On-the-road testing of the effects of driver's experience， gender， speed， and road grade on car emissions[J]. Journal of the Air & Waste Management Association， 2019，69（10）：1182-1194.

[12] LOMAN M， ŠARKAN B， SKRUCANY T. Comparison of fuel consumption of a passenger car depending on the driving style of the driver[J]. Transportation Research Procedia， 2021，55：458-465.

[13] CHENG R， GEN M， TOZAWA T. Vehicle routing problem with fuzzy due-time using genetic algorithms[J]. Journal of Japan Society for Fuzzy Theory and Systems， 1995，7（5）：1050-1061.

[14] 邱玉琢，张磊. 碳排放规制下生鲜农产品配送车辆路径优化问题[J]. 南京财经大学学报，2021（1）：68-78.

[15] XIAO Y， ZHAO Q， KAKU I， et al. Development of a fuel consumption optimization model for the capacitated vehicle routing problem[J]. Computers & Operations Research， 2012，39（7）：1419-1431.

[16] MOHAMMADI M， RAZMI J， TAVAKKOLI-MOGHADDAM R. Multi-objective invasive weed optimization for stochastic green hub location routing problem with simultaneous pick-ups and deliveries[J]. Economic Computation & Economic Cybernetics Studies & Research， 2013，47（3）：247-266.

[17] 吴丽荣，胡祥培，饶卫振. 考虑燃料消耗率的车辆路径问题模型与求解[J]. 系统工程学报，2013，28（6）：804-811.

[18] 张金良，李超. 碳排放影响下的动态配送车辆路径优化研究[J]. 中国管理科学，2022，30（9）：184-194.

[19] 丁澍，邱玉琢. 考虑低碳的多目标冷链混合车队路径规划研究[J/OL]. 计算机工程与应用：1-13[2023-09-13]. http：//kns.cnki.net/kcms/detail/11.2127.TP.20230517.1459.013.html.

[20] HICKMAN J， HASSEL D， JOUMARD R， et al. Methodology for calculating transport emissions and energy consumption[R]. Brussels， Belgium， 1999.

[21] KOURIDIS C， GKATZOFLIbq/mcfE7KQzKUXgcIJPBBA==AS D， KIOUTSIOUKIS I， et al. Uncertainty estimates and guidance for road transport emission calculations[R]. European Commission Joint Research Centre Institute for Environment and Sustainability， 2010.

[22] 周果，季彬，方晓平. 多对多越库配送绿色车辆路径问题及算法研究[J]. 铁道科学与工程学报，2022，19（8）：2202-2210.

[23] BOWYER D P， BIGGS D C， AKÇELIK R. Guide to fuel consumption analyses for urban traffic management[R]. Australian Road Research Board Transport Research， 1985.

[24] BARTH M， BORIBOONSOMSIN K. Real-world carbon dioxide impacts of traffic congestion[J]. Transportation Research Record， 2008，2058（1）：163-171.

[25] BANDEIRA J， ALMEIDA T G， KHATTAK A J， et al. Generating emissions information for route selection： Experimental monitoring and routes characterization[J]. Journal of Intelligent Transportation Systems， 2013，17（1）：3-17.

[26] 唐金环. 基于减排驱动的选址-路径-库存集成问题模型与求解研究[D]. 沈阳：东北大学，2017.

[27] NIU Y， YANG Z， CHEN P， et al. Optimizing the green open vehicle routing problem with time windows by minimizing comprehensive routing cost[J]. Journal of Cleaner Production， 2018，171：962-971.

[28] 周鲜成，蒋涛营，贺彩虹，等. 冷链物流配送的绿色车辆路径模型及其求解算法[J]. 中国管理科学，2023（12）：203-214.

[29] XIAO Y， KONAK A. A genetic algorithm with exact dynamic programming for the green vehicle routing & scheduling problem[J]. Journal of Cleaner Production， 2017，167（20）：1450-1463.

[30] KOÇ Ç， KARAOGLAN I. The green vehicle routing problem： A heuristic based exact solution approach[J]. Applied Soft Computing， 2016，39：154-164.

[31] 穆东，王超，王胜春，等. 基于并行模拟退火算法求解时间依赖型车辆路径问题[J]. 计算机集成制造系统，2015，21（6）：1626-1636.

[32] PU X， LU X， HAN G. An improved optimization algorithm for a multi-depot vehicle routing problem considering carbon emissions[J]. Environmental Science and Pollution Research， 2022，29（36）：54940-54955.

[33] 唐慧玲，唐恒书，朱兴亮. 基于改进蚁群算法的低碳车辆路径问题研究[J]. 中国管理科学，2021，29（7）：118-127.

[34] WANG X， LI X. Carbon reduction in the location routing problem with heterogeneous fleet， simultaneous pickup-delivery and time windows[J]. Procedia Computer Science， 2017，112：1131-1140.