基于城市复合网络的出行交通分配组合模型研究

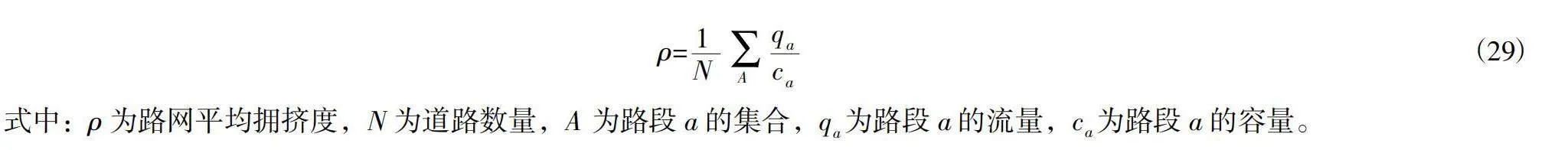
摘 要：文章提出了一种交通分配组合模型，解决传统四阶段方法缺乏联系导致误差逐渐放大的问题。文章基于构建的城市复合网络，将交通方式划分和交通分配整合在一起，综合考虑交通方式选择和交通分配的影响。通过基于A*算法的备选路径集查找方法，求解给定OD上的k短路径情况。采用广义费用公式对多方式出行效用进行计算，将费用、时间和换乘行为进行统一量化。最后，建立交通方式划分与交通分配组合模型，采用多层次迭代平衡求解，优化交通方式分担率。算例分析验证了组合模型在流量分配方面的优势，具有更好的路段流量均衡性和较低的阻抗时间。该模型可为城市交通规划和出行预测提供参考。

关键词：复合网络；交通方式划分；交通分配组合模型；A*算法

中图分类号：F502 文献标志码：A

DOI：10.13714/j.cnki.1002-3100.2024.19.018

Abstract： This article proposes a traffic allocation combination model to solve the problem of errors gradually amplifying due to the lack of connection in traditional four stage methods. This model integrates the division of transportation modes and transportation allocation， constructs a composite network， and comprehensively considers the impact of transportation mode selection and transportation allocation. Solve the k-short path situation on a given OD using an alternative path set search method based on the A* algorithm. Using the generalized cost formula to calculate the utility of multimodal travel， the cost， time， and transfer behavior are uniformly quantified. Finally， establish a combination model of traffic mode division and traffic allocation， and use multi-level iterative equilibrium solution to optimize the sharing rate of traffic modes. The example analysis verifies the advantages of the combined model in traffic allocation， with better road flow balance and lower impedance time. This model can provide reference for urban transportation planning and travel prediction.

Key words： composite network; traffic mode division; traffic allocation combination model; A star algorithm

0 引 言

传统交通需求预测方法将交通需求预测划分为四个独立的阶段：交通产生、交通分布、交通方式划分和交通分配。这种方法在实践中被广泛应用，因为它具有清晰的逻辑和明确的数据流入流出关系。然而，随着交通预测精度要求的提高，传统四阶段之间缺乏联系所带来的误差逐渐放大，因此需要建立新的模型来整合这四个阶段，以减少误差[1]。

近年来，有学者将交通四阶段需求预测中的两个或多个步骤组合起来，建立新的组合预测模型，减少传统四阶段中缺少联系造成的偏差。杜刚诚等[2]将交通分布中的重力模型与交通分配中的用户均衡模型组合起来建立一个新的熵模型，但是模型只对步骤进行简单改进，喻翔等[3]提出了基于广义费用的交通方式划分和交通分配组合模型，并做了简单算例求解，王炜等[4]结合交运之星平台对步行、自行车、机动车和公共交通等多种交通方式进行一体化分配。传统研究中交通方式划分的结果对交通分配阶段只能影响其平均值，在特定OD下，交通方式还受到道路流量的影响，形成循环反馈的关系，因此，需要建立一个更加完善的组合模型进行建模分析。

此外，在以往的研究中，交通方式划分通常采用分层Logit模型。这种方法需要先对私家车和公共交通比例进行分配，然后再考虑同层次公交分配问题，这是由于不同公交车的IIA特性引起的[5]。随着超级网络概念的提出，交通方式划分开始转向链接不同子网络的方法。孟梦等[6]构建了组合出行模式的超级网络，通过给定广义费用公式进行方式划分。袁春毅等[7]通过连接公路、铁路、水运和民航等建立超级网络模型，为国家级客运货运提供战略参考。

汪勤政等[8]基于换乘约束网络建立多方式交通分配模型算法；何胜学[9]考虑环境影响，建立交通需求分布和流量分配组合模型。早期的交通组合往往局限于数据的获取，并未做实际验证，随着数据采集技术和大数据技术的发展，居民出行调查、交通路网等数据更易被获取，交通分配模型的研究也更为完善；在公交地铁成网的交通系统里，原有的独立方式划分需要改进，建立符合实际情况的多方式复合网络进行研究分析。

本文使用开放街道地图（OSM）路网数据和公交地铁站点数据，引入了虚拟边的概念，将交通换乘行为考虑进模型中，建立了复合交通网络，对城市路网的k短路径寻找算法进行改进，确定了各起讫点的可行路径集。建立了交通方式划分与交通分配组合模型，在交通流量迭代平衡中，对每一次迭代交通方式比例进行重分配，体现两个交通阶段循环影响。本文旨在通过建立复合路网和组合模型，提高交通预测的精度，优化预测机制，并为后续研究提供参考。

1 路网构建与备选路径集查找

1.1 复合网络的构建

道路网络的准确性和完整性对于模拟和评估交通系统的性能至关重要。开放街道地图（OSM）提供了大量道路交叉口的经纬度坐标数据，为构建道路网络提供了便利。本小节的目的是利用OSM地图数据构建道路网络，并将其与公交和地铁网络相结合，以建立公交——地铁复合网络并进行换乘分析。

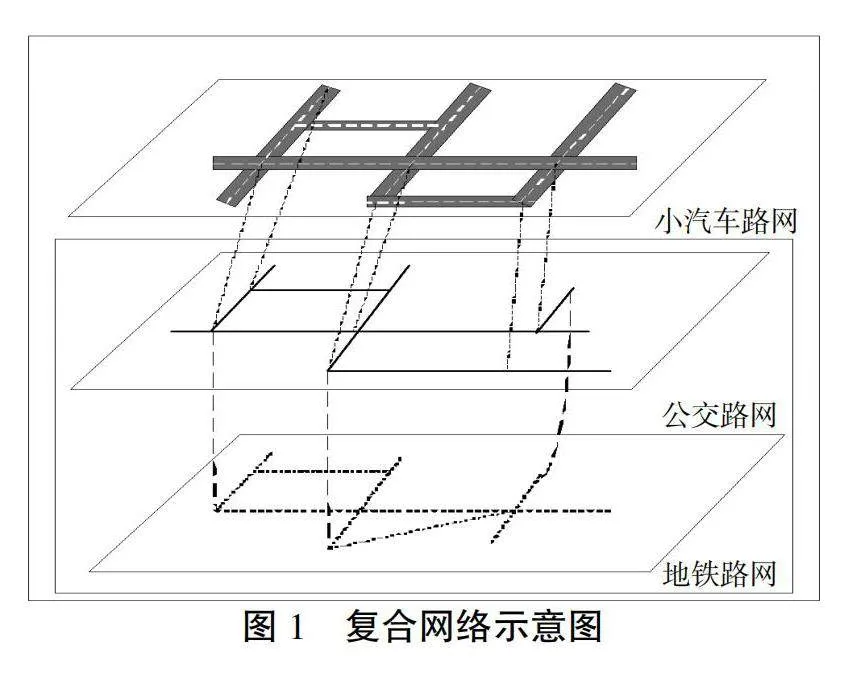
复合网络包括多个子网络，每个子网络都是一个独立的系统，并通过一些节点与其他子网络进行交互。通过提供多样化的交通选择，复合网络能够提供更丰富的交通方式组合，从而改善交通方式划分的准确性和实用性。复合网络示意图如图1所示。

本文复合网络由三个子网络构成，每个子网络都具有自己独立的边和节点属性。为了考虑出行者的换乘行为，需要在公交子网络和地铁子网络之间构建虚拟边。这些虚拟边表示换乘路径，用于连接公交和地铁之间的换乘点。通过引入换乘网络和虚拟边，复合网络可以更准确地模拟和评估出行者在公交和地铁之间的换乘行为。这种方式使得模型能够综合考虑不同交通方式之间的换乘损失，并为出行者提供更全面的交通选择。

（1）小汽车子网络构建

建立基于OSM地图数据的小汽车网络G=V，E，W，网络节点数据代表交叉路口，两节点间的连接边代表现实道路，其权重为道路阻抗，网络节点强度和连边权重可以反映节点和连接边的通行能力，其数学模型如下：

式中：i、j为交叉路口，V为节点集合，E为连接边集合，A为邻接矩阵，W为加权邻接矩阵，L为路段长度，V为路段限速，Q为路段实时流量，C为路段容量，m、n为公式参数，一般取值0.15和4。

（2）公交与地铁复合网络构建

基于已有的公交地铁站点数据与路线数据，建立公交网络G=V，E，W和地铁边G=V，E，W，网络节点数据代表公交或地铁站点，两节点间的连接边表示公交或地铁线路的一部分，其权重为路段通行时间，其数学模型如下：

对于公交和地铁间的换乘行为，引入换乘虚拟边矩阵：

式中：i、j为公交地铁站点，V为节点集合，E为连接边集合，A为邻接矩阵，W为加权邻接矩阵，f为i、j两站点间发车频率，L为地铁站点i、j间的长度，U为地铁站点i、j间的路段运行速度。δ为换乘最大距离，L为两站点间步行换乘距离，v为步行速度。

1.2 基于A*算法的备选k短路径集查找

在交通方式划分问题中，我们需要确定备选路径集，求解给定OD上的k短路径情况。在以往的k短路径集寻找问题中，往往采用偏离路径Yen算法，基于Dijkstra算法获取最短路径，并在最短路径中进行“偏离”，隐藏最短路径中偏离点到终点这一部分路径，再次使用Dijkstra算法获得次短路径，从而达到获取k短路的结果[10]。对于大规模网络而言，Dijkstra算法中通过每一次局部最优解得到全局最优解的方法存在收敛过慢的问题，为了解决这一问题，本文使用A*算法替代Dijkstra算法作为最短路径寻找方法，A*算法考虑了启发式函数对路径寻优的影响，能够更快的得到最优解，从而降低时间复杂度，更适用于城市大规模路网问题。

对于路网G=V，E，W偏离路径的Yen算法步骤如下：

Step1：根据A*算法求得起讫点r，s之间的最短路径，将该路径编号为p，并放入k短路径集合P中，此时i=1；

Step2：取集合P中的最后一条路径p作为当前路径，将该路径中除终点t之外的所有节点g作为潜在偏离节点，使用A*算法求得从各个节点g到终点s的最短路径作为偏离最短路径，为避免与前面路径重合，在使用A*算法前，需要隐藏g，s部分路径；

Step3：将偏离最短路径与未偏离路径r，g连接，作为第i条最短路径的候选路径之一，并将该路径放入候选路径集合X中；

Step4：从集合X中选择长度最小的路径作为第i+1条最短路径p，将该路径放入最短路径集合P中；

Step5：若集合P的路径总数m=k，则算法结束，否则返回Step2。

上述步骤中，使用A*算法代替了传统Dijkstra算法，A*算法的效用函数如下：

F=G+H （17）

G=w， a∈p （18）

H=φ （19）

式中：F为选择下一节点的效用函数，G为从起点移动到指定节点的阻抗，H为下一节点到终点的估算距离，p为起点r到当前节点n的路径集，φ为当前节点n到终点s的曼哈顿距离。H为该算法的启发式函数，通过终点距离这一先验条件，避免算法寻找局部最优而远离终点。依次从起点计算下一节点，直至到达终点。

2 交通分配组合模型的建立

2.1 复合路网交通方式选择

在建立复合路网之后，地铁、公交、小汽车为同一层次网络，地铁公交不再具有IIA特性，引用广义函数对多方式出行效用进行计算，将费用、时间、换乘行为进行统一量化，更好的体现交通方式带来的优势。OD对r，s间k条路径的广义费用计算公式如下：

式中：V为OD对r，s间p类交通方式的广义费用，p为OD对r，s间p类交通方式的票价费用，T为OD对r，s间p类交通方式的时间费用，ω为OD对r，s间p类交通方式的换乘费用。

小汽车出行票价：

P=H*S （21）

公共交通出行票价为：

P=H*L+H*L （22）

式中：H为小汽车每公里花费的燃油费，S为OD对r，s路径k出行距离；H为公交车每条线路乘车的花费，L为OD对r，s路径k的公交线路数，H为地铁每条线路乘车的花费，L为OD对r，s路径k的地铁线路数。

换乘延误：对于虚拟边带来的换乘延误，采用出行距离与换乘次数的比值计算成本：

ω= （23）

式中：ω为换乘延误成本，t为公共交通单次换乘花费时间，n为OD对r，s上路径k的换乘次数。

根据MNL模型计算OD对之间选择不同路径的概率，出行者选择不同方式的概率计算公式如下：

P= （24）

式中：P为OD对r，s出行者选择方式p的概率，N为出行方式的总量，λ为服从尺度参数。

2.2 方式划分与交通分配组合求解

本文旨在综合考虑出行方式选择和交通分配的影响，建立一种交通方式划分与交通分配组合模型，以研究出行者在实际出行中对不同线路的调整和交通方式的选择行为。该模型考虑不同路线对于不同交通方式的效用指数，以实现对出行路径的选择研究。

在组合模型中，出行方式选择作为交通分配的一部分，需要考虑交通方式对不同路段负载情况的影响。传统MSA方法只考虑单一交通方式的迭代平衡，而在MSA的迭代过程中，由于上一次迭代影响了道路阻抗，从而对交通方式划分结果产生影响，故每一次迭代中，需要对交通方式进行再分配。

交通分配求解目标为每一条路段阻抗函数的积分累加最小值：

minZ=w （25）

由于MSA针对的是单一交通方式带来的流量更新，需考虑公共交通与小汽车两种流程分配方案：

X=X+X （26）

式中：X为第i次流量分配方案，X为第i次公共交通流量分配方案，X为第i次小汽车流量分配方案。对于给定的流量总数Q，在每一次迭代时有：

= （27）

下一次迭代流量更新公式为：

式中：Y为第i次公共交通最优流量方案，Y为第i次小汽车最优流量方案，μ为公共交通当量转换系数。

整体步骤如下：

Step1：对于给定的OD对r，s和流量Q，根据k短路径计算备选路径集P。此时i=1；

Step2：根据备选路径集属性，将总流量Q按交通方式划分算法分为小汽车流量Q和公共交通流量Q；

Step3：分别对小汽车和公交-地铁两种方式进行交通分配，得到初始方案X；

Step4：将公共交通流量转换为小汽车当量，对路网进行流量更新，得到路网流量分布Q；

Step5：i=i+1，重新执行Step1～Step4，得到拟分配的辅助方案Y，新的流量分配方案X=X+Y-X/i；

Step6：根据新的流量分配方案，更新得到新的路网流量分布Q，若两次流量的结果之差小于设定阈值，即Q-Q<ε，则组合模型达到最优解，否则返回Step5。

3 算例分析

3.1 场景描述

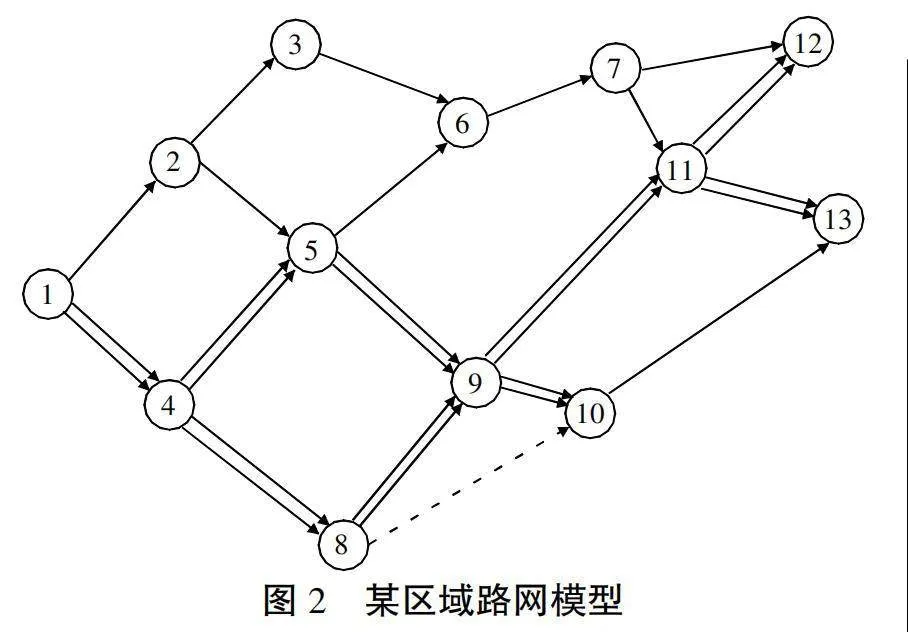
本文采用某区域部分路网数据验证本文的正确性和方法的有效性。部分路网如图2所示，经过简化后获得如图2所示路网，双线代表路段同时属于小汽车与公共交通路网，该路网包括13个节点和18个路段，设置了道路容量、自由流阻抗、道路属性等，各路段属性如表1所示。选取OD对1，12，1，13，4，13进行分析。

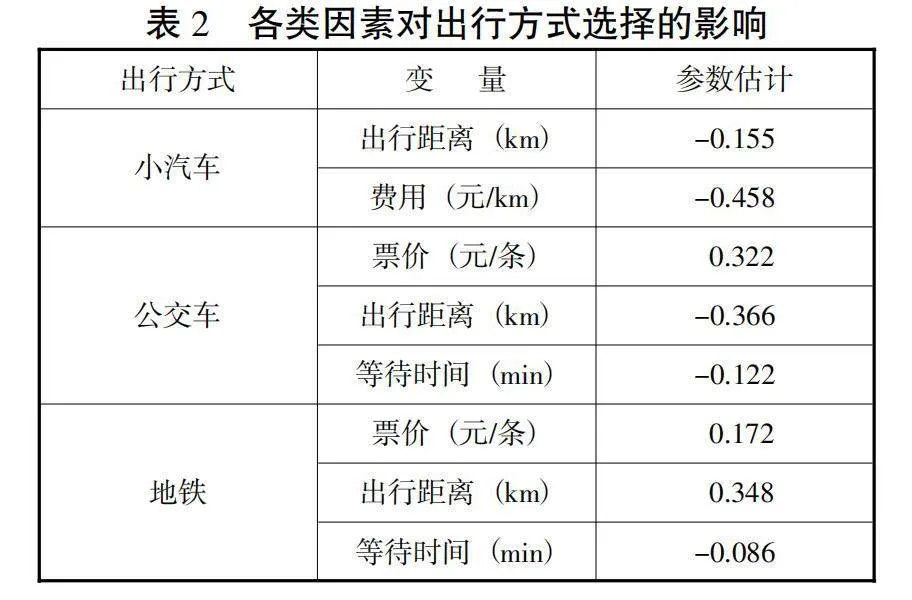
对研究区域以往的出行方式进行出行调查，主要考虑三种出行方式（小汽车、公交车、地铁），以及对应的距离、费用、等待时间等进行因素，参数如表2所示。

在各种出行方式中，小汽车变量参数均为负值，表明随着时间、费用、距离的增加、出行者选择该交通方式的概率降低。其中费用对小汽车影响最大，在长出行距离时，出行者更偏向于选择地铁这一交通方式。通过上述参数标定结果，可分析影响出行者在出行过程中对出行方式和路径选择的关键因素进行量化分析，为后续多方式交通分配的出行路径选择奠定基础。

3.2 结果分析

基于本文第二章的组合模型，λ取值0.1，分配流量Q为500pcu时，对研究区域三个OD分配情况进行求解，算法在迭代第18次时达到初步收敛，精度为0.05，道路平均拥堵率约为0.63，在80次迭代时达到0.01的迭代精度要求，道路平均拥堵率为0.608。算法在一般精度情况下具有良好的求解速度。其中平均拥挤度计算公式为：

ρ= （29）

式中：ρ为路网平均拥挤度，N为道路数量，A为路段a的集合，q为路段a的流量，c为路段a的容量。

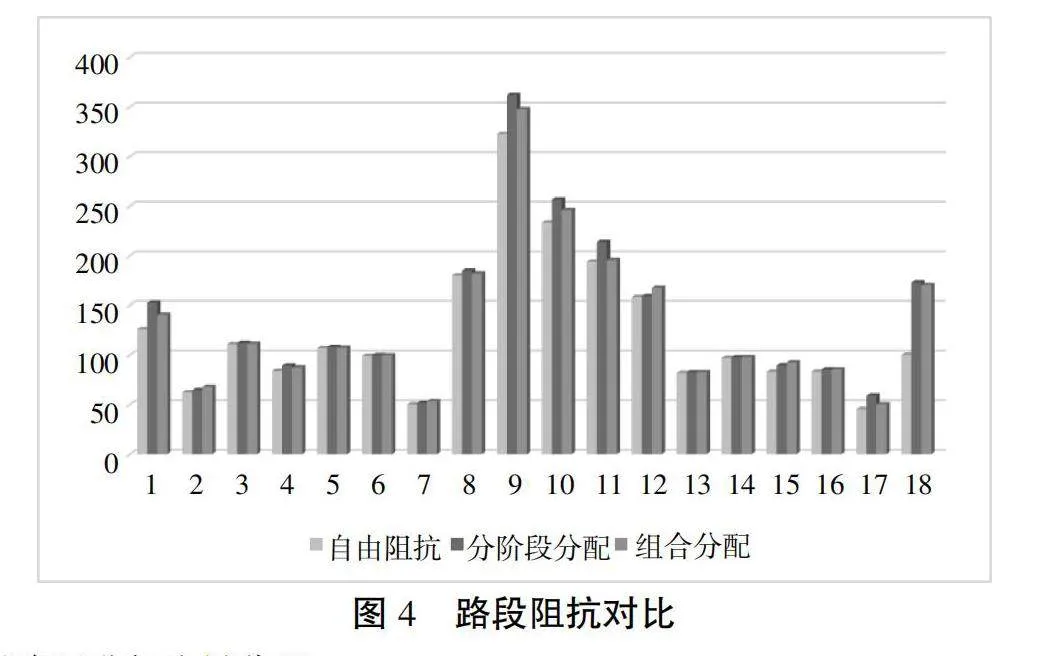
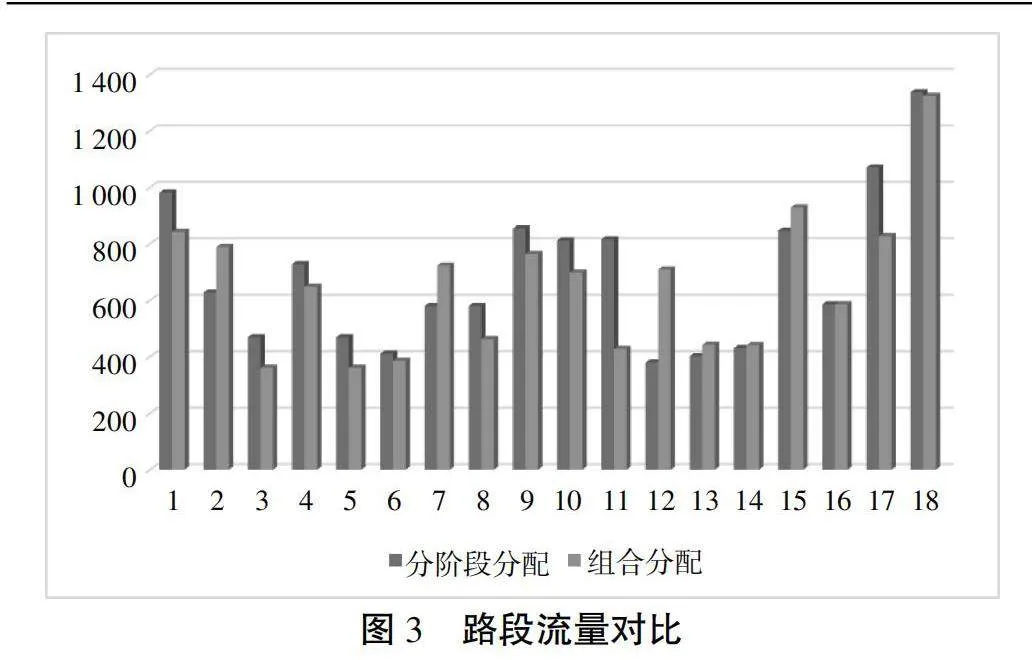
与传统分阶段交通分配进行比较，将两种方法分别用于研究区域进行流量分配，不同路段流量与阻抗情况如图3、图4所示。

图3、图4为分方式分配与组合分配的结果对比，从图3可知，分方式分配存在路段流量分布不均衡的情况，分阶段分配的流量区间在380～1 330pcu，流量分布标准差为264，组合分配的流量区间在360～1 320pcu，流量分布标准差为249；图4中，组合分配的阻抗时间普遍低于分阶段分配。这是由于组合模型中，对交通方式进行重新划分，优化不同交通方式分担率，从而达到更优的路网流量比例，优化阻抗时间。

此外，在对城市大规模问题进行求解时，往往不会找到所有路径，存在分配不完全问题，采用组合模型由于每次进行交通方式划分会重新迭代，选定新的路径集，故而能更加全面的利用路网进行流量分配。

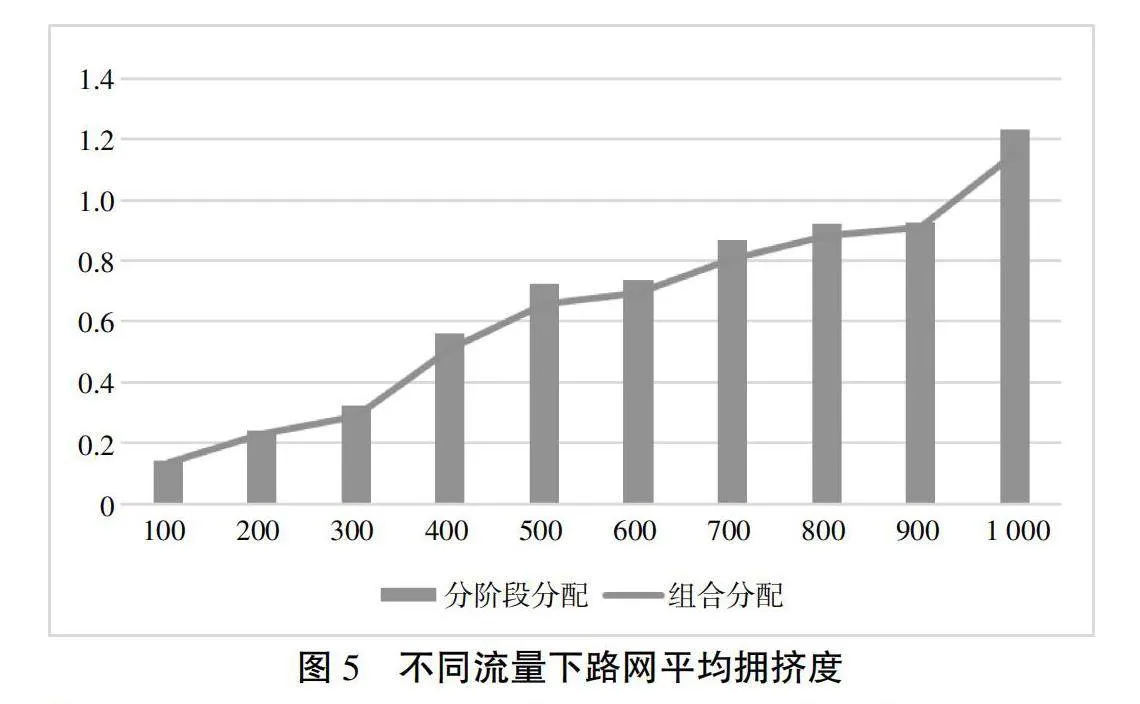
当继续加大流量时，对路网拥堵程度进行分析，验证算法结果中路段堵塞程度随流量的变化。

从图5可知，组合模型在相同的流量输入情况下，会有更低的路段拥挤度，由于交通分配的结果会对交通方式分担率进行动态调整，从而达到更合理的小汽车与公共交通分担比例。在分两阶段的交通分配中，小汽车与公共交通的路段流量只能达到各自方式的最优解，而达不到全方式的最优解。

4 结论与展望

本文基于复合网络和交通分配组合模型，对交通需求预测进行了研究。通过整合公交、地铁和小汽车网络，并引入虚拟边来考虑换乘行为，建立了复合网络，提高了交通预测的精度和实用性。采用基于A*算法的备选路径集查找方法，优化了路径选择过程，使得模型能够更快速地求解给定OD上的k短路径情况。通过广义费用公式统一量化费用、时间和换乘行为，提高了交通方式选择的准确性。算例分析表明，相比传统的分阶段交通分配方法，本文提出的组合模型具有更好的路段流量均衡性和较低的阻抗时间。组合模型能够动态调整交通方式分担率，实现更合理的交通方式选择，优化了路网流量分配，减轻了交通拥堵现象。

虽然本文的组合模型取得了一定优势，但仍有改进空间。可以考虑更全面整合交通方式，如出租车、共享单车等，以反映城市交通出行的多样性。优化路网数据选择，采用更丰富的实时交通数据和人流数据，提高模型的预测精度。交通方式划分模型的标定可以进一步考虑更多因素的影响，以提高对出行者心理和行为的理解和预测能力。文中组合模型采用了多层次迭代平衡求解方法，可以考虑引入更高效的优化算法和并行计算技术，提高求解效率。

综上所述，本文的交通分配组合模型为城市交通规划和出行预测提供了参考，但仍有许多方面可以进一步完善和探索，以提高交通预测的精度和实用性。

参考文献：

[1] 刘丽华，王炜，华雪东，等. 城市交通需求预测理论与模型研究综述[J]. 科学技术与工程，2021，21（30）：12804-12813.

[2] 杜刚诚，彭国雄. 交通组合模型在交通需求预测中的应用研究[J]. 武汉理工大学学报（交通科学与工程版），2004（1）：92-94，144.

[3] 喻翔，毛敏，刘建兵. 城市交通需求预测组合模型的研究[J]. 西南交通大学学报，2003（1）：75-79.

[4] 王炜，王建，华雪东，等. 基于网络交通分配方法族谱的交通分配一体化技术与工程应用[J]. 交通运输系统工程与信息，2021，21（5）：30-39.

[5] 姚丽亚，孙立山，关宏志. 基于分层Logit模型的交通方式选择行为研究[J]. 武汉理工大学学报（交通科学与工程版），2010，34（4）：738-741.

[6] 孟梦，邵春福，曾静靖，等. 组合出行模式下多方式交通流分配模型及算法[J]. 吉林大学学报（工学版），2014，44（1）：47-53.

[7] 袁春毅，聂向军，邵春福，等. 基于多方式广义费用模型的超级交通网络需求预测技术应用[J]. 中国公路学报，2022，35（11）：228-238.

[8] 汪勤政，四兵锋. 换乘约束下城市多方式交通分配模型与算法[J]. 交通运输系统工程与信息，2017，17（4）：159-165，181.

[9] 何胜学. 环境影响的交通需求分布和流量分配组合模型及算法研究[J]. 交通节能与环保，2020，16（4）：49-54.

[10] 徐涛，丁晓璐，李建伏. K最短路径算法综述[J]. 计算机工程与设计，2013，34（11）：3900-3906，3911.