基于深度强化学习带时间窗的绿色车辆路径问题研究

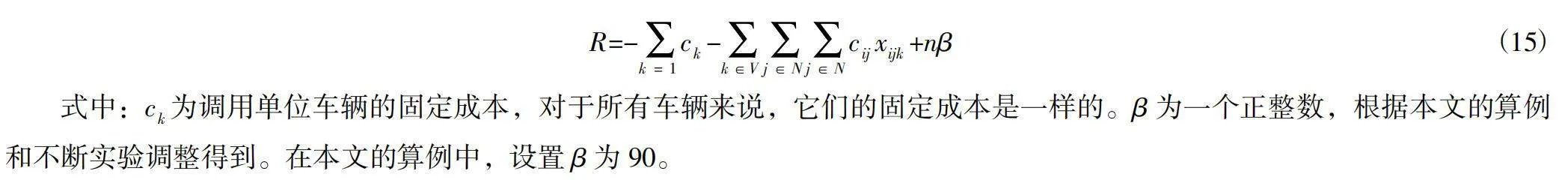
摘 要：如何在客户规定的时间内合理安排车辆运输路线，一直是物流领域亟待解决的问题。基于此，文章提出使用基于软更新策略的决斗双重深度Q网络（Dueling Double Deep Q-network， D3QN），设计动作空间、状态空间与奖励函数，对带时间窗的绿色车辆路径问题进行建模与求解。选择了小、中、大规模的总计18个算例，将三种算法的实验结果在平均奖励、平均调度车辆数、平均里程和运算时间四个维度进行比较。实验结果表明：在大多数算例中，与Double DQN和Dueling DQN相比，D3QN能在可接受的增加时间范围内，获得更高的奖励函数，调度更少的车辆数，运输更短的里程，实现绿色调度的目标。

关键词：深度强化学习；路径优化；决斗双重深度Q网络；D3QN算法；车辆路径问题

中图分类号：U116.2 文献标志码：A DOI：10.13714/j.cnki.1002-3100.2024.19.017

Abstract： How to reasonably arrange vehicle transportation routes within the time specified by customers has always been an urgent problem in the field of logistics. Based on this， this paper proposes to use Dueling Double Deep Q-network（D3QN）based on soft update strategy to design action space， state space and reward function to model and solve the green vehicle routing problem with time window. A total of 18 small， medium and large scale examples are selected， and the experimental results of the three algorithms are compared in four dimensions： Average reward， average number of scheduled vehicles， average mileage and operation time. The experimental results show that， in most examples， compared with Double DQN and Dueling DQN， D3QN can obtain higher reward function， dispatch fewer vehicles， transport shorter mileage， and achieve the goal of green dispatch within the range of acceptable increase in time.

Key words： deep reinforcement learning; path optimization; Dueling Double Deep Q network; D3QN algorithm; vehicle routing problem

0 引 言

带时间窗的车辆路径问题（Vehicle Routing Problems with Time Windows，VRPTW）是指在时间窗口约束下，将一定数量的配送或服务点分配给若干个车辆，使得所有配送或服务点被访问一次，并满足各车辆容量约束条件的配送路径问题。VRPTW问题最早可以追溯到20世纪70年代末和80年代初，它通常基于图论建立数学模型，是一个典型的NP-hard问题。

随着计算机算力的提升，深度学习算法逐步用于解决实际问题。2013年，Mnih et al.[1]首次提出了深度Q网络（Deep Q

-network）模型，该模型是一个卷积神经网络，用Q学习的变体训练，成功地直接从高维感觉输入中学习控制策略。2016年，Silver et al.[2]将深度强化学习算法运用到围棋游戏中，并且引入了蒙特卡洛树搜索法。在此算法的基础上，他们编写了程序AlphaGo。同年3月，AlphaGo以4比1的总比分战胜了围棋世界冠军李世石，成为第一个直接击败人类选手的人工智能机器人。由于传统的Q学习算法在某些情况下会高估动作值，从而使得整体的决策无法达到最优，Hasselt et al.[3]提出了深度双Q网络（Double DQN， DDQN）算法。Wang et al.[4]提出了对决深度Q网络（Dueling DQN）算法，这种算法能够更准确地估计状态的价值，区分不同动作的重要性。

强化学习的经典算法包括深度Q网络，在此基础上又衍生出了深度双Q网络，决斗深度Q网络和决斗双重深度Q网络等。决斗双重深度Q网络作为前两者算法的演化与升级，在其他领域取得了优于前二者算法的表现。袁帅等[5]借助带经验回放机制的D3QN算法，实现移动机器人在未知环境中更好地获取最优路径。在收敛速度方面，相比DQN提升了56%。韩磊等[6]使用改进的D3QN算法，提升了可变限速控制策略的灵活性。此外，也有学者将强化学习的方法运用到经典的路径优化问题中。Kool et al.[7]使用借助基于注意力机制和指针网络的强化学习解决旅行社问题，其结果接近其他专业算法。Nazari et al.[8]提出了一个端到端的强化学习框架来解决车辆路径问题，该模型仅通过观察奖励信号并遵循可行性规则，就可以从给定分布中采样问题实例找到接近最优的解决方案。其计算质量优于经典的启发式方法和Google的OR-Tools，并且计算时间相当。Lin et al.[9]运用深度强化学习研究电动汽车车队的路径优化问题，所提出的模型能够有效解决现有方法难以求解的大规模调度问题。

带时间窗的车辆路径问题作为一个经典的物流领域调度规划问题，不少学者使用精确式算法、近似算法对该问题及其变种问题进行建模和求解。随着环保理念的深入，学者们对考虑环境影响、碳排放的车辆路径优化问题也逐渐深入，车辆路径优化问题逐渐向着绿色调度的方向发展。

此外，随着人工智能技术的发展，强化学习的方法逐步运用到路径优化问题的求解中，并且取得了一定的成效。以往的研究往往借助基础的深度Q网络，对VRPTW问题进行求解，该方法容易造成对Q值的高估，从而降低训练的质量。双重深度Q网络算法作为一种新兴的算法，在解决此类问题上仍然有较大的潜力。传统的深度Q网络使用的是硬更新的方式对目标网络进行更新。本文运用了基于策略的深度强化学习方法中的参数更新方式，使用基于软更新策略的决斗双重深度Q网络算法，定义状态空间、动作空间和奖励函数，借助算法的智能体决策解决带时间窗的运输问题，验证了该算法在解决带时间窗的绿色车辆路径问题上的有效性。

1 算法概述

1.1 深度双Q网络与竞争深度Q网络

在原始的DQN算法中，由于原始算法采用的是新策略的方法，容易出现Q值估计偏高的情形。算法每次在学习时，不是使用下一次交互使用的真实动作，而是使用当前策略认为的价值最大的动作，产生最大化偏差，使得估计动作的Q值偏大。

为了解决这个问题，将动作选择和价值估计进行解耦，Hasselt等提出了深度双Q网络。DDQN算法相较于DQN算法，改变了目标值的计算方法，这使得训练过程更加稳定，能够有效地解决后者对于动作价值的高估问题，提高了算法的收敛性和性能。

DDQN基于经验回放机制与目标网络技巧，构建两个动作价值神经网络，一个用于估计动作，另外一个用于估计该动作的价值。DDQN算法不直接通过最大化的方式选取目标网络计算的所有可能Q值，而是首先通过评估网络选取最大Q值对应的动作。

接着，再将评估网络选择出的动作a，输入目标网络计算目标值：

式中：y表示目标值，w表示评估网络参数，w表示目标网络参数。

Dueling DQN算法是传统DQN的一个拓展，它包含了一种新的神经网络结构——竞争网络（Duel Network）。Dueling DQN通过引入一个基准网络和一个优势网络，将值函数的估计分解为状态值和动作优势。状态值表示在给定状态下的期望回报，而动作优势表示每个动作相对于平均值的优劣程度。通过这种分解，Dueling DQN可以将注意力集中在对状态值的学习上，而无需为每个动作单独计算值。这使得算法更加高效，并且能够更好地处理动作空间较大的环境。Dueling DQN的评估网络结构如下：

式中：V为最优状态价值函数，A为最优优势函数，第三项为在动作a平均取值情况下的优势函数，一般为0。

1.2 软更新策略的决斗双重深度Q网络

决斗双重深度Q网络（D3QN）结合了Double DQN和Dueling DQN算法的思想，进一步提升了算法的性能，是二者的演化与升级。它与Dueling DQN算法的唯一区别在于计算目标值的方式，其目标网络计算方式借鉴了Double DQN的思想，即利用评估网络获取s状态下最优动作价值对应的动作，然后利用目标网络计算该动作的动作价值，从而得到目标值。

本文使用基于软更新策略的D3QN来解决VRPTW问题。D3QN的目标网络与评估网络的模型和参数完全一致。这两个网络的更新方式包括硬更新和软更新，本文采取软更新的方式对评估网络的参数进行更新。评估网络的参数每更新迭代一次，目标网络的参数也会随之更新。软更新通过在每次更新时将一小部分评估网络的参数与目标网络的参数进行混合，从而使目标网络的更新过程平滑化。这种混合比例由超参数tau控制。具体更新公式如下：

w=tau*w+1-tau*w （4）

软更新可以减轻强化学习算法中的不稳定性问题。尽管相比于硬更新，其学习速度可能相对较慢，但如软更新在训练过程中提供了一种平滑的、逐渐更新的方式，更能增加算法的稳定性。

2 带时间窗的绿色车辆路径问题描述

2.1 问题描述

本文所研究的带时间窗的绿色车辆路径问题，在规划路线过程中考虑了环境保护和可持续性的因素，旨在最小化运输成本的同时，减少运输过程中的碳排放。绿色车辆问题的优化可以通过车辆调度和路径规划、车辆种类的选择以及燃料消耗等方面实现，降低对环境的影响[10]。在本文的模型中，所有的配送车辆被认为是相同的，因此，它们的排放量也相同。对于绿色车辆路径问题，本文的攻克重点放在车辆的调度数量和路线的距离上。车辆启动所排放的二氧化碳量是固定的，因此，调度越少的车辆，服务单位客户的碳排放越低。基于此，本文模型的优化目标为：首先实现调度车辆数量最小化，其次实现运输路线距离最小化，以期实现对环境的最小影响。奖励与惩罚函数的设置也关系到模型的优劣程度。本文对于车辆的调度成本设置为120个单位，而服务单个客户的成本为90个单位。对于智能体而言，需要服务至少两个客户，才能实现正收益，进一步保证了运输的有效性和调度的绿色性。

VRPTW问题的模型目标为：设计一组使总成本最小化的路线，首先最小化调度车辆数，其次最小化总运输距离。该问题的其他调度规则有：

每一个顾客仅服务一次；

每一条路线从0节点开始，到n+1节点结束；

能够实时观测到客户的时间窗，车辆的容量限制；

车辆在节点之间的移动距离在数值上等同于移动所花费的时间。

VRPTW问题的模型如下：

式（5）为目标函数，表明模型的目标是最小化总运输成本。式（6）确保每一个客户仅被访问一次。式（7）表明单一车辆的运输上限为它的容量上限。式（8）、式（9）和式（10）表明单一运输车辆必须从车库0出发，在服务客户后，最终回到车库节点n+1。式（11）建立了从上一个客户到下一个客户的车辆离开时间的关系。式（12）确保车辆服务时间在顾客的时间窗内。式（13）表明x为一个决策变量，保证单个车辆服务对应的客户。式（14）规定了多个变量的取值范围。

2.2 D3QN求解目标问题

使用D3QN算法求解带时间窗的绿色车辆路径问题，需要对算法的状态空间与动作空间、奖励函数两个方面进行重新设计。本节也从这两各方面进行介绍。

状态空间与动作空间方面，本文的状态空间指的是将车辆进行调度，服务顾客的过程中所处状态的集合。在本文问题中，车辆的状态为访问顾客的序列，长度为n。本文定义：在一辆车出发后，服务顾客，最终回到仓库时，车辆的坐标更新，容量重置为初始容量，调度时间归零，调度车辆序号增加1。

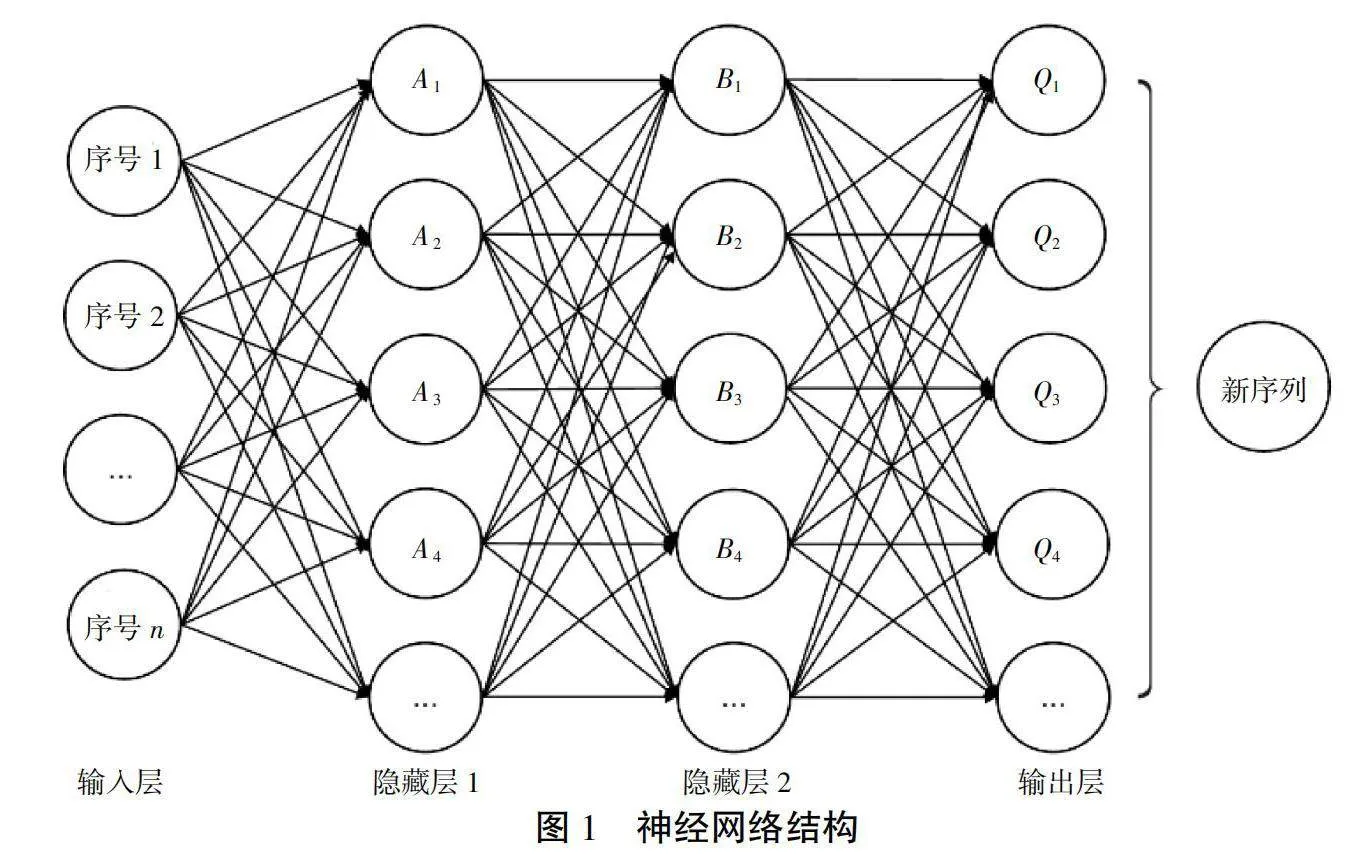
本文的动作空间定义为：将访问序列输入神经网络D60+iQ6532T6fe0KTWa+RohNF66HWZiwyOj1lIJa4os=，与环境进行交互所得到新的访问序列。动作空间的维度也为n，它会随着训练集中顾客数量的增加而增加。神经网络输出层输出的是采取动作a的情况下，进入下一个状态s可能选择的各种动作所对应的Q值大小。车辆将持续选择Q值最大的动作，更新位置与奖励。神经网络结构如图1所示。

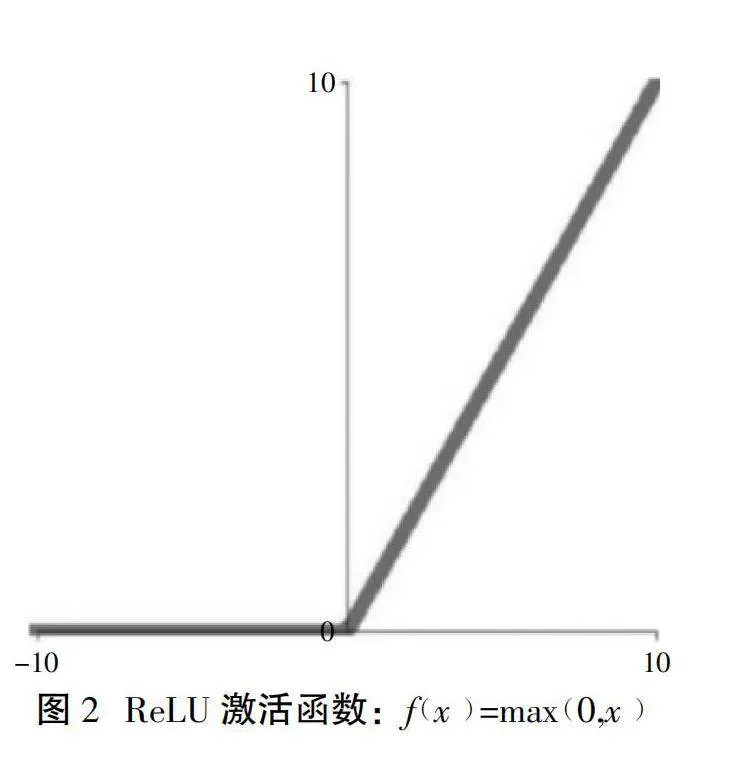
车辆状态输入神经网络后，通过ReLU函数激活（见图2），传递给下一个隐藏层或输出层。当车辆容量无法满足下一个顾客的需求，或是奖励过小时，车辆将直接返回仓库（0号节点），并调度下一辆车进行服务。

车辆每进行一次服务，将更新一次车辆移动的总距离，进行一次奖励函数的计算和累计，更新一次车辆的服务顺序序列，更新一次车内的剩余容量。

奖励函数的设置方面，深度强化学习的目标是最大化累计奖励。奖励函数的设置会影响到模型的学习效果。本文模型的实现目标为：首先实现调度车辆数量最小化，其次实现总运输距离最小化。前者的优先级要高于后者。基于这个原则，智能体在训练过程中调用的车辆越多，调度成本越高，惩罚应当越大；所有车辆运输的总距离越短，奖励越大。这两个部分作为公式的第一项和第二项，以负整数的形式表示。由于在本模型中，车辆行驶距离长短的数值等同于所花费的时间，因此，车辆的行驶距离越短，也意味着所花费的时间越少。在公式的第三项中，车辆每服务一个客户，进行一次固定的奖励。

本文研究问题的时间窗为硬时间窗，即车辆只能在规定时间内为客户服务。因此，提前到达客户地点的车辆，需要等待到客户的服务时间窗，才能进行服务，对于这部分车辆，不进行惩罚。

因此，将D3QN的累计奖励函数设置为三部分之和，具体公式如下：

R=-c-cx+nβ （15）

式中：c为调用单位车辆的固定成本，对于所有车辆来说，它们的固定成本是一样的。β为一个正整数，根据本文的算例和不断实验调整得到。在本文的算例中，设置β为90。

2.3 研究与算法流程

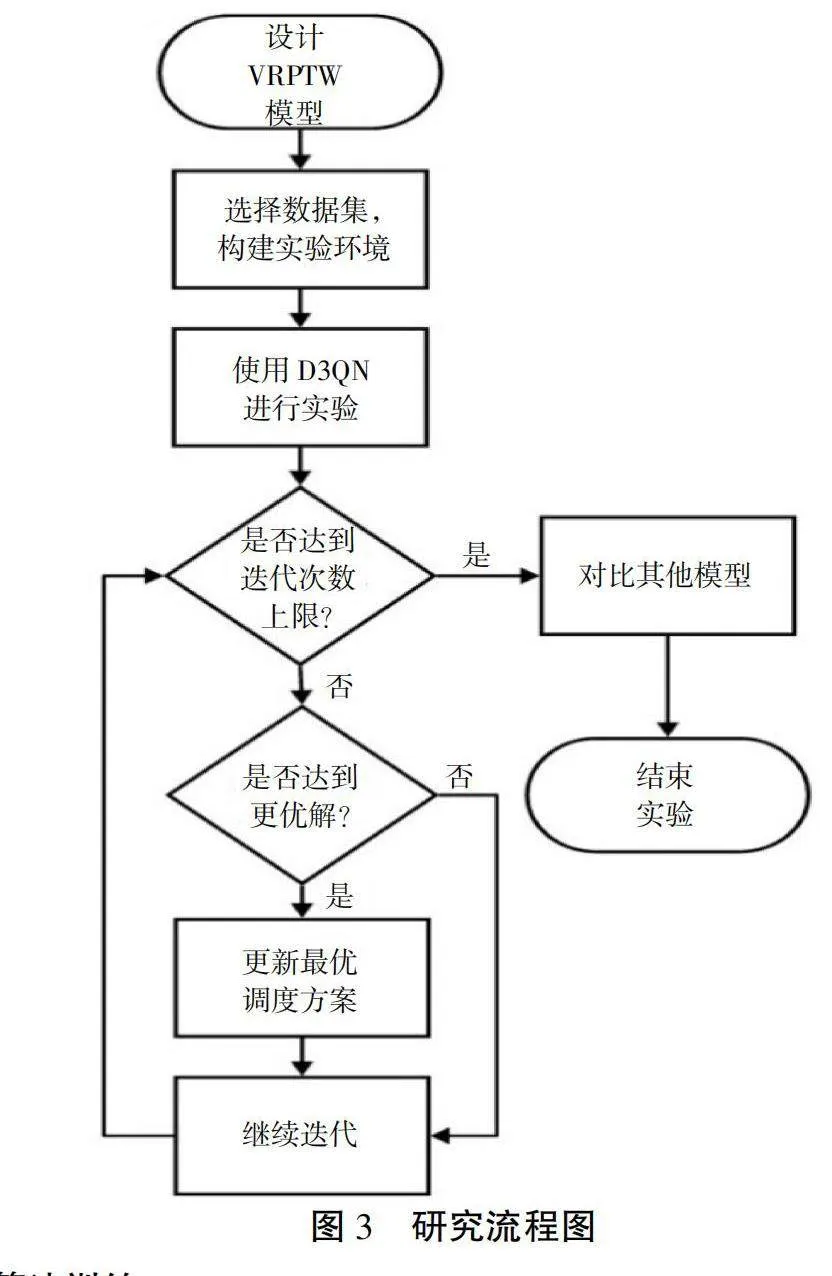
本文的研究流程如图3所示。

本文算法的伪代码如表1所示。

3 算法训练

3.1 算法模型与参数设置

本文应用算法为基于软更新策略的决斗双重深度Q网络，基于Python3.9语言与Pytorch1.13框架实现，配置12th Gen Intel（R）Core（TM）i9-12900H 2.50 GHz，RAM 16.0GB。VRPTW模型借助Python中的gym库进行编译。

探索策略方面，本文使用ε-贪心策略（epsilon-greedy）来对目标问题进行求解。

式中：ε为一个小于1的正数，P=ε表示算法以ε的概率随机选择动作空间的动作，P=1-ε表示算法以1-ε的概率选择当前时间步内价值最大的动作作为下个时间步要执行的动作。

算法方面，D3QN的评估网络共有四层网络结构。算法的第一层为输入层，共有四个输入维度，分别是：当前车辆所在节点的序号、车内的实时容量、当前的时间以及当前调度车辆的序号。算法的第二层、第三层和第四层为隐藏层，它们都是有128个神经元结点的全连接层，使用ReLU函数进行激活。算法的第五层为输出层，输出层输出的是对于各个动作的价值评估，输出维度会随着客户数量的变化而变化。根据各个动作的价值，智能体选择价值最高的动作采取下一步的行动。本文使用Adam优化器进行梯度下降法的求解。

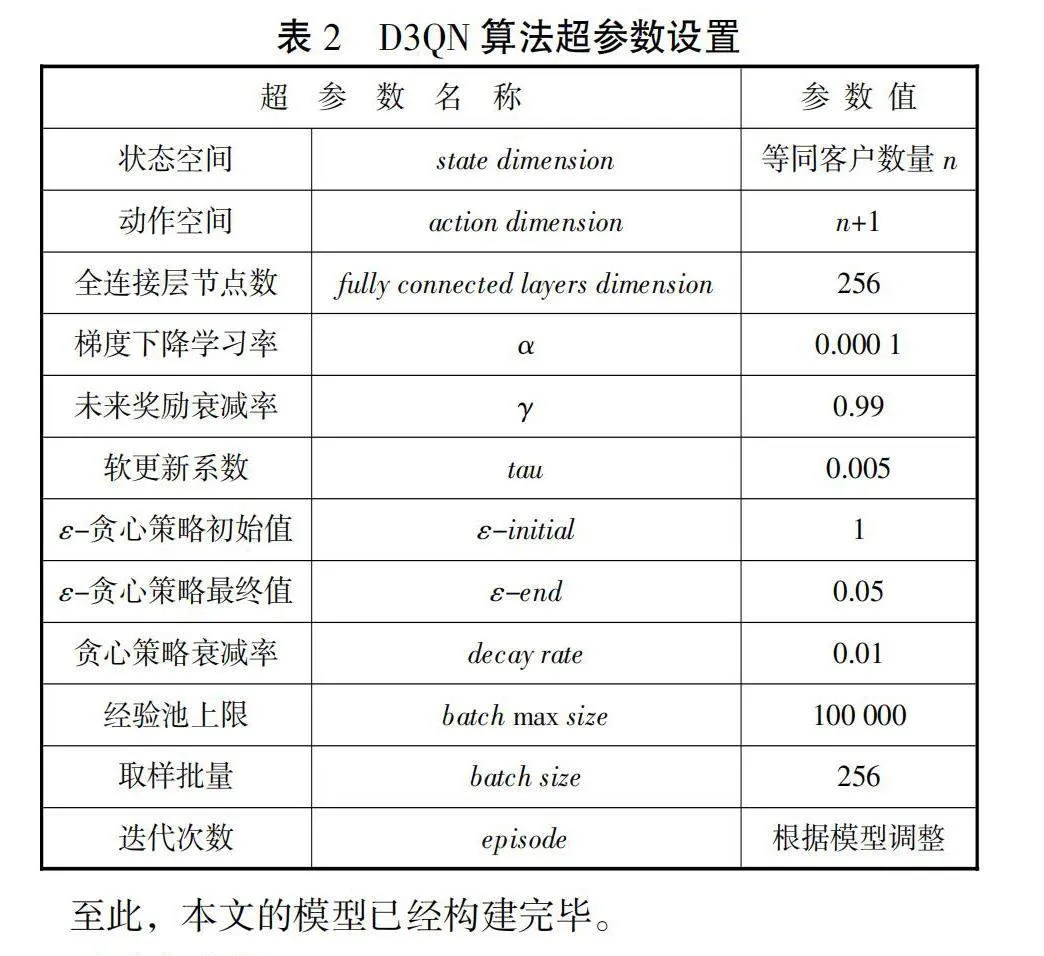
D3QN算法的超参数设置如表2所示。

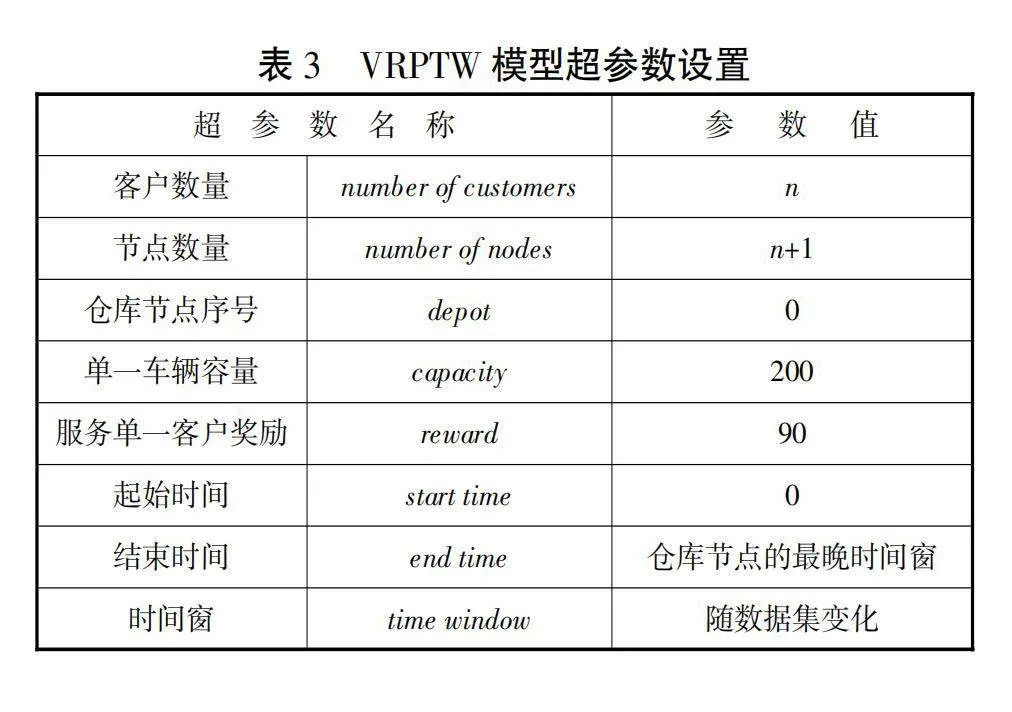
模型方面，借助gym库，构建了VRPTW模型的虚拟环境，以便接入强化学习算法中进行训练。本文选择了客户数量分别为10、20和50的多个数据集，分别代表小规模，中规模和大规模调度问题，以便验证算法在不同规模上的性能。越大规模的问题，智能体获得奖励的函数趋近收敛所需要的实验迭代次数越多。因此，针对不同规模的调度问题，本文也设置了不同的约束和实验的迭代次数。模型的部分超参数如表3所示。

至此，本文的模型已经构建完毕。

3.2 实验与分析

本文选择了Double DQN以及Dueling DQN算法，将它们与D3QN算法在不同问题规模的数据集上进行对比实验，以检验D3QN算法在解决此类问题上的优越性。

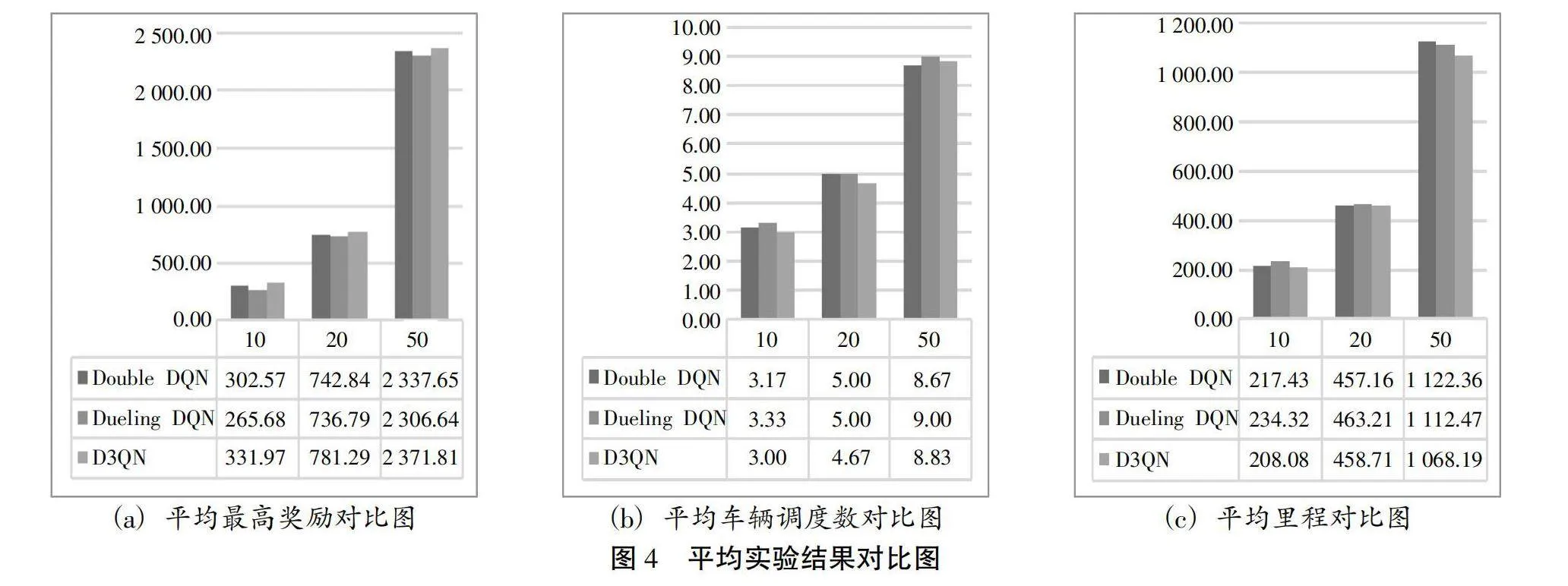
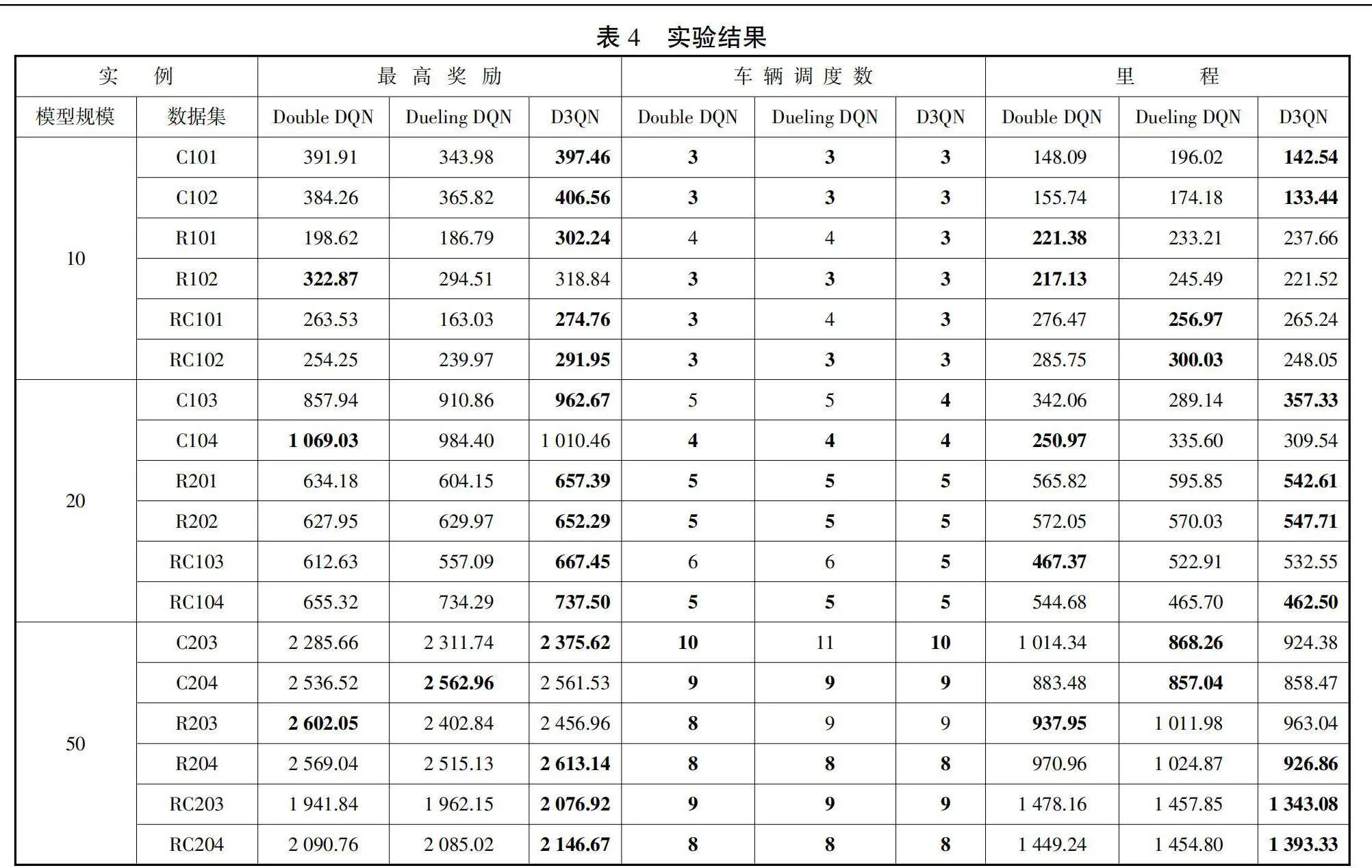
在表4所展示的18个不同规模的实验结果中，有14个实例中，D3QN取得了最高的奖励，占总实验次数的77.8%。由于本文实验的研究目标为：首先最小化调度车辆数量，其次最小化运输距离。因此，基于研究问题的绿色性原则，取得最高奖励的实验案例，运输里程未必最短。将三种算法在不同规模实例下的实验结果进行平均取值，具体结果如图4所示：

从图4发现：在平均最高奖励方面，D3QN算法比Double DQN高5.45%，比Dueling DQN高11.27%；在平均车辆调度数方面，D3QN算法比Double DQN低3.34%，比Dueling DQN低6.17%；在平均里程方面，D3QN算法比Double DQN低2.93%，比Dueling DQN低5.38%。

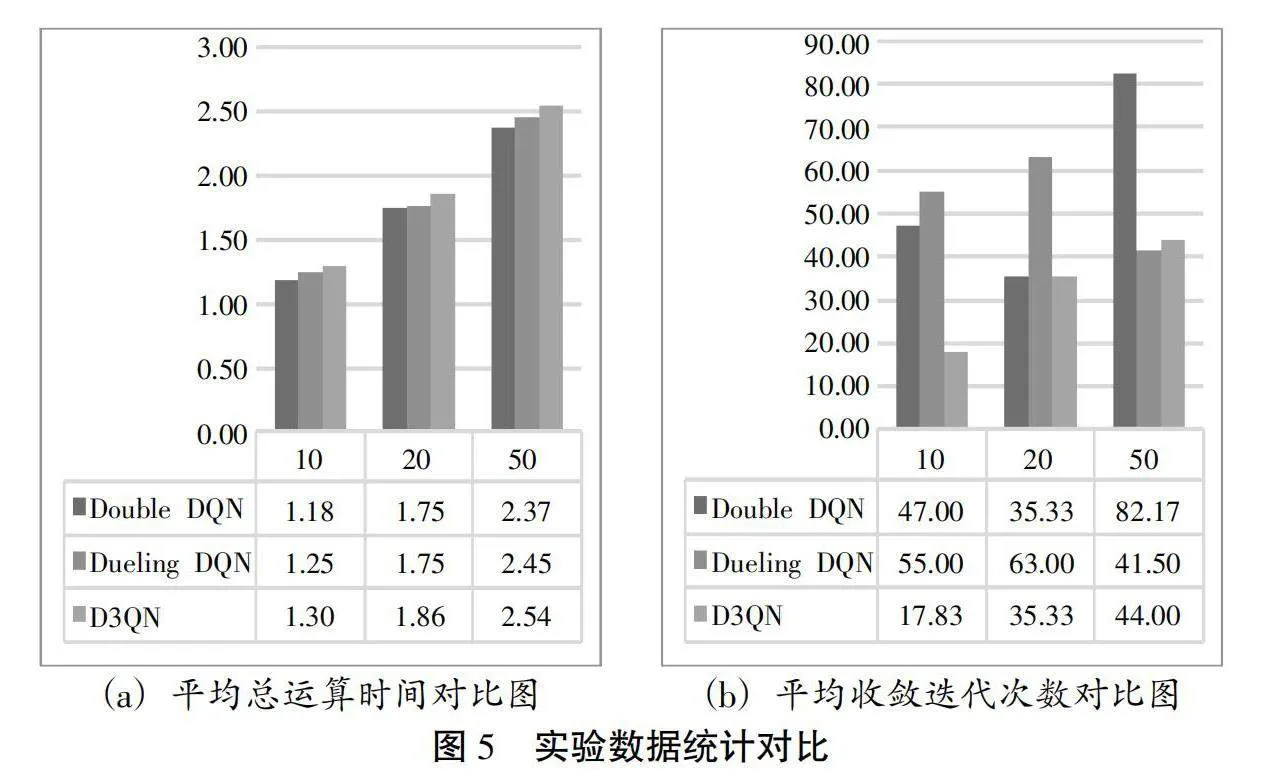
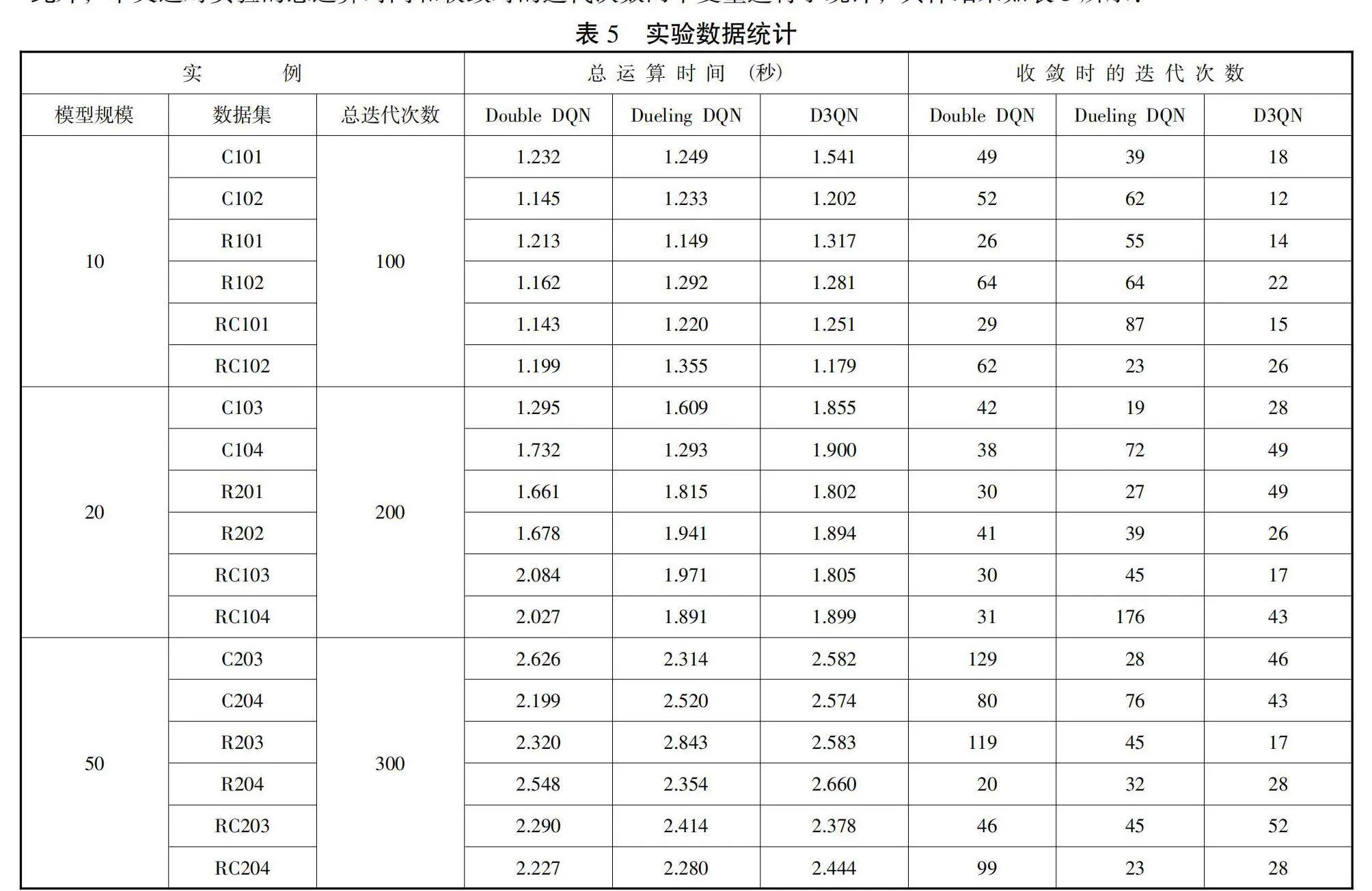
此外，本文还对实验的总运算时间和收敛时的迭代次数两个变量进行了统计，具体结果如表5所示：

 ; 本文分别设置模型规模为10、20、50的算例的总迭代次数为100、200和300次。总体而言，三种算法总运算时间较短，收敛时的迭代次数较快。将统计数据进行平均取值，具体结果展示如图5所示。

从图5中发现：在平均总运算时间方面，D3QN比Double DQN多7.71%，绝对值为0.13s，比Dueling DQN多4.35%，绝对值为0.08s；在平均收敛迭代次数方面，D3QN比Double DQN少36.17%，比Dueling DQN少35.16%。造成这种结果的原因可能是算法的结构不同。D3QN算法作为后两者算法的组合，其计算复杂度要更高，因而会耗费更长的时间。但是，从绝对数值的角度分析，D3QN多增加的运算时间平均保持在0.15s内，在实际应用中处于可接受范围内。此外，由于D3QN算法比后两者算法收敛速度要快，因此，在减少相同迭代次数的情况下，D3QN算法会比后两者算法花费更少的时间收敛。

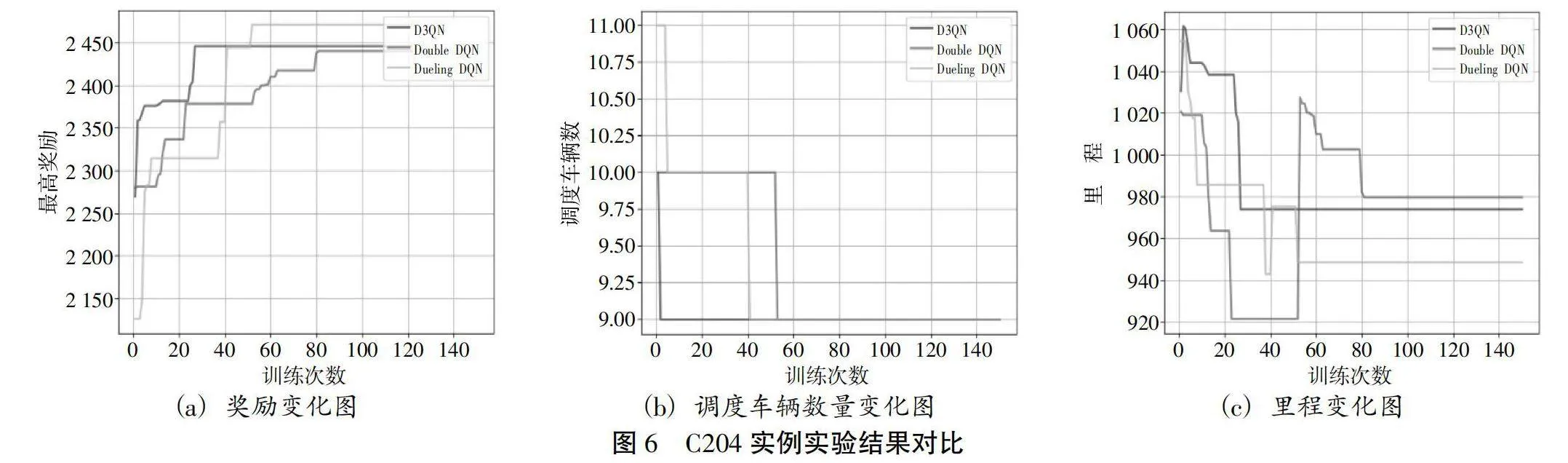
图6展示了在客户为50个的问题下，以C204数据进行实验的三种算法的奖励变化、调度车辆变化以及里程的变化。为了更直观地展示实验效果，本文设置实验次数为150轮。在前40轮中，D3QN算法最高奖励的上升速度较快，并且最先收敛。在此实例的实验中，三种算法所得到的最高奖励值接近，且用时均在2s以内。在图6（c）中，里程变化是上下波动的，因为调度车辆的减少可能导致奖励值和运输里程的增加。这也印证了本文研究问题的绿色性。

通过上述表格以及图，得出结论：在可接受的增加运算时间的情况下，基于软更新策略的D3QN算法相比于Double DQN和Dueling DQN算法能更快的收敛，得出更优的解。在带时间窗的绿色车辆路径优化问题中，D3QN算法相比于后两者算法更具备优越性。前者在算法层面结合了后者的优点。由于强化学习算法的探索具有一定的随机性，算法的表现基于不同的算例可能有差异。同时，算法的表现也受到实验参数、奖励函数、训练次数和深度以及计算机性能等方面因素的影响。随着这些因素的不断调整与优化，算法的表现也会越来越好。

4 结论与展望

本文使用基于软更新策略的D3QN算法对带时间窗的绿色车辆路径问题进行研究，将车辆的调度问题转化成顾客访问的排序问题；通过设置奖励函数，优先实现最小化调度车辆的目标，保证运输的绿色低碳；借助Python中的gym库，使算法的智能体与环境进行交互，重新规划序列。D3QN算法结合了Double DQN和Dueling DQN算法的技巧。在大部分算例中，D3QN算法在此类问题上的表现要优于这二者，能更快地寻找到更优质量的解。

本文的主要贡献如下：

（1）使用D3QN算法为带时间窗的绿色车辆路径问题设计了相应的动作空间与状态空间和奖励函数，能够较好地将问题转化为强化学习中智能体的运算与迭代。

（2）使用软更新的策略对D3QN算法的评估网络参数进行更新，能保证算法的稳定性和收敛性。

（3）在小、中、大的共18个数据集上进行了实验，将Double DQN与Dueling DQN作为对比，验证了D3QN算法的有效性。

综上所述，D3QN算法在解决VRPTW问题上仍然有较大的潜力。随着模型的优化和计算机算力的提升，该算法的性能也会进一步提升。

参考文献：

[1] MNIH V， KAVUKCUOGLU K， SILVER D， et al. Playing atari with deep reinforcement learning[EB/OL]. （2021-12-19）[2023-09-20]. https：//arXiv.org/pdf/1312.5602.pdf.

[2] SILVER D， HUANG A， MADDISON C， et al. Mastering the game of go with deep neural networks and tree search[J]. Nature， 2016，529：484-489.

[3] VAN HASSELT H， GUEZ A， SILVER D. Deep reinforcement learning with double q-learning[C] // Proceedings of the AAAI Conference on Artificial Lintelligence， 2016.

[4] WANG Z， SCHAUL T， HESSEL M， et al. Dueling network architectures for deep reinforcement learning[C] // International Conference on Machine Learning PMLR， 2016：1995-2003.

[5] 袁帅，张莉莉，顾琦然，等. 移动机器人优先采样D3QN路径规划方法研究[J]. 小型微型计算机系统，2023，44（5）：923-929.

[6] 韩磊，张轮，郭为安. 混合交通流环境下基于改进强化学习的可变限速控制策略[J]. 交通运输系统工程与信息，2023，23（3）：110-122.

[7] KOOL W， VAN HOOF H， WELLING M. Attention， learn to solve routing problems！[EB/OL]. （2021-10-24）[2003-09-20]. https：//github.com/wouterkool/attention-learn-to-route.

[8] NAZARI M， OROOJLOOY A， SNYDER L， et al. Reinforcement learning for solving the vehicle routing problem[EB/OL]. （2023-09-08）[2023-09-20]. https：//github.com/optML Group/VRP-RL.

[9] LIN B， GHADDAR B， NATHWANI J. Deep reinforcement learning for the electric vehicle routing problem with time windows[J]. IEEE Transactions on Intelligent Transportation Systems， 2021，23（8）：11528-11538.

[10] ASGHARI M， AL-E S M J M. Green vehicle routing problem： A state-of-the-art review[J]. International Journal of Production Economics， 2021，231：107899.

[11] SOLOMONMM. Vehicle routing and scheduling with time window constraints： Imodels and algorithms （heuris tics）[D]. University of Pennsylvania， 1984.

[12] SAVELSBERGH M W P. The vehicle routing problem with time windows： Minimizing route duration[J]. ORSA Journal on Computing， 1992，4（2）：146-154.

[13] MARTIN DESROCHERS， JACQUES DESROSIERS， MARIUS SOLOMON. A new optimization algorithm for the vehicle routing problem with time windows[J]. Operations Research， 1992，40（2）：342-354.

[14] K C TAN， L H LEE， K OU. Artificial intelligence heuristics insolving vehicle routing problems with time window constraints[J]. Engineering Applications of Artificial Intelligence， 2001，14（6）：825-837.

[15] 刘虹庆，王世民. 基于强化学习的车辆路径规划问题研究[J]. 计算机应用与软件，2021，38（8）：303-308.

[16] SAMUEL A L. Some studies in machine learning using the game of checkers[J]. IBM Journal of Research and Development， 1959，3（3）：210-229.

[17] WATKINS C J C H， DAYAN P. Q-learning[J]. Machine Learning， 1992（8）：279-292.

[18] HUANG Y， WEI G L， WANG Y X. VD D3QN： The variant of double deep q-learning network with dueling architecture

[C] // 第37届中国控制会议论文集（F），2018.

[19] KALLEHAUGE B， LARSEN J， MADSEN O B G， et al. Vehicle routing problem with time windows[M]. Springer US， 2005.

[20] 韩岩峰. 基于深度强化学习的无人物流车队配送路径规划研究[D]. 大连：大连理工大学，2021.

[21] 周瑶瑶，李烨. 基于排序优先经验回放的竞争深度Q网络学习[J]. 计算机应用研究，2020，37（2）：486-488.

[22] 冯超. 强化学习精要[M]. 北京：电子工业出版社，2018.

[23] 刘驰，王占健，戴子彭. 深度强化学习学术前沿与实战应用[M]. 北京：机械工业出版社，2020.

[24] YANG S， XU Z， WANG J. Intelligent decision-making of scheduling for dynamic permutation flowshop via deep reinforcement learning[J]. Sensors， 2021，21（3）：1019.

[25] 孙沪增，李章维，秦子豪，等. 带时间窗车辆路径规划算法研究与实现[J]. 小型微型计算机7a4019138b4b6d4f1e2855f6b56a0e9290d1caf14133d0fb1134951c9679e173系统，2020（5）：972-977.

[26] TICHA H B， ABSI N， FEILLET D， et al. Multigraph modeling and adaptive large neighborhood search for the vehicle routing problem with time windows[J]. Computers & Operations Research， 2019，104：113-122.

[27] 李茹杨，彭慧民，李仁刚，等. 强化学习算法与应用综述[J]. 计算机系统应用，2020，29（12）：17-29.

[28] BURSUC A， GUETTIER C， et al. Optimal solving of constrained path-planning problemswith graph convolutional networks and optimized tree search[C] // 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems （IROS）， IEEE， 2019：3519-3525.