基于订单相似度的AutoStore系统订单分批问题研究

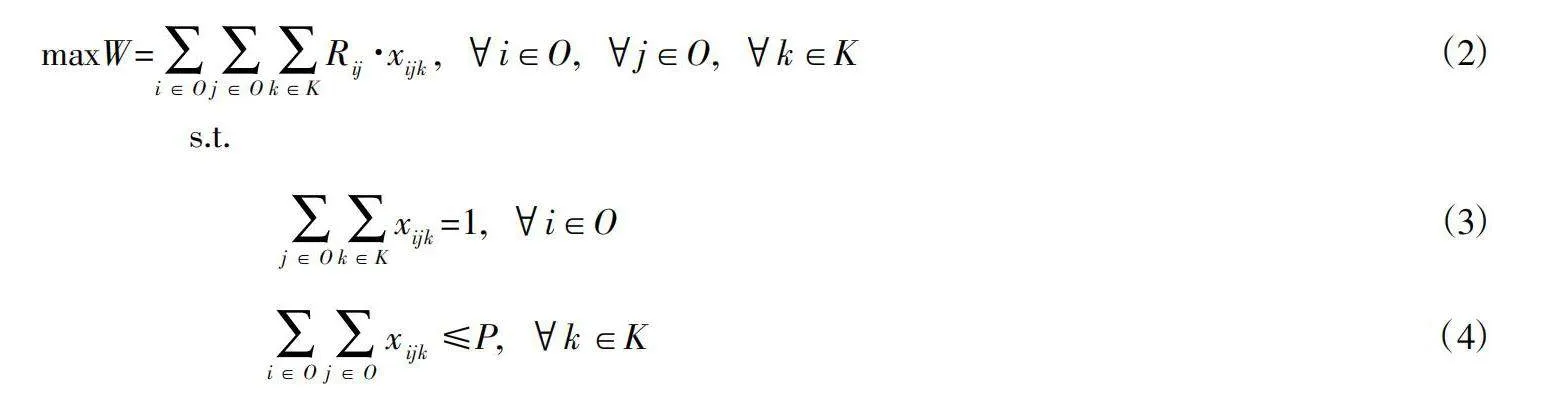
摘 要：作为一种高度自动化、智能化的高密度存储系统，AutoStore系统受到电商企业广泛关注。相较传统仓库，该系统能显著提高效率、降低成本。为进一步优化其效率，针对AutoStore系统中订单分批问题，以最大化单批订单相似度为目标构建了混合整数线性规划模型，并设计了基于层次聚类的启发式算法进行求解。根据现实订单数据设置了多个不同规模算例，通过实验证明了算法可行性。结果表明对不同规模订单分批问题，所提出算法均可在短时间内取得较优解。

关键词：AutoStore仓储系统；订单分批；混合整数规划模型；启发式算法；聚类算法

中图分类号：F253.9 文献标志码：A DOI：10.13714/j.cnki.1002-3100.2024.19.009

Abstract： In the realm of contemporary logistics， the AutoStore system， characterized by its advanced automation and intelligent high-density storage capacities， has garnered substantial attention from e-commerce enterprises. When juxtaposed with conventional warehousing systems， the AutoStore demonstrates a pronounced enhancement in operational efficiency while concurrently driving down associated costs. In an endeavor to amplify its efficacy， we addressed the intricate order batching issue inherent to the

AutoStore system. A mixed-integer linear programming model was meticulously formulated， predicated on the objective of optimizing the homogeneity within individual order batches. To achieve an effective resolution， we conceived and implemented a heuristic algorithm anchored in hierarchical clustering methodologies. Empirical validations， predicated on real-world order data across diverse scales， substantiated the algorithm's practicability. Preliminary outcomes indicate that irrespective of the order batch scale， our proffered algorithm consistently delivers superior solutions in abbreviated timeframes.

Key words： AutoStore warehousing system; order batching; mixed-integer programming model; heuristic algorithm; clustering algorithm

0 引 言

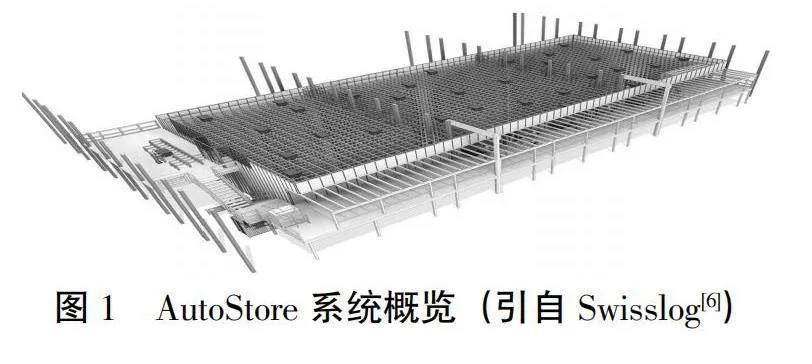
《中国制造2025》国家发展战略中明确指出，为促使我国工业制造产能提升，需要进一步推进智能物流发展[1]。在这一战略导向下，众多电商企业将物联网（IoT）和人工智能（AI）等前沿技术投入到智能物流设备和系统的研发中，以提升物流的自动化和智能化程度[2]。其中一种成果为AutoStore系统，这是一种高度自动化、智能化且储存密度极高的系统[3]。如图1所示，AutoStore通过纵向堆叠最多十五个规格相同的标准储物箱来构建储存堆垛，并将这些堆垛连接组成一个空间利用率极高的储存系统[4]。该系统中可以通过放置隔板，将料箱内部分隔成不同的小区域，从而在同一个料箱中存储多个种类货品[5]。

在传统仓库中的订单拣选通常会面临一系列问题，其中首要问题是低效率[7]。传统拣选系统通常采取“人到货”拣货方式，这意味着工人需要从工作台移动到储存区域进行拣货，导致工人在仓库中进行大量重复移动，产生大量的时间和劳动力浪费[8]。此外，传统仓库通常不能灵活应对订单变化情况，当订单量增加或SKU种类增多时，这些仓库很难临时扩展，可能需要重新设计布局及增加更多工人[3]。另外，当某个订单需要优先处理时，传统系统难以快速调整拣选优先级。最后，拣货在整个仓库运营中的成本占比相当大，通常占仓库运营成本一半以上[9]。

对于上述问题，AutoStore系统凭借其高度自动化和紧凑的系统设计，可以提供较好的解决方案。首先，通过机器人将料箱送至工作台的“货到人”方式，可以显著提高拣选效率，减少了时间和劳动力的浪费[10]。同时，由于机器人可以垂直和水平方向移动，可以随时根据需求调度到相应的存储货位，结合AutoStore系统高度模块化的特性，整个系统具有很高的灵活性，能够根据不同的优先级和订单需求快速调整拣货方案[4]。最后，由于应用了大量自动拣货机器人代替人工，该系统的拣货成本大大低于传统仓库[11]。

订单拣选效率的提高是现代物流和供应链管理中的关键问题，为进一步提高订单拣选效率，通常可以采用订单分批的策略。它的核心理念是将含有相同种类货物的多个订单集中在同一个波次中进行处理。现阶段，国内外许多学者针对不同智能仓储系统对该问题进行过深入研究。Petersen et al.[12]的研究表明，在人工拣选系统中，对于小批量订单进行订单分批能显著节省总成本。这为订单分批的实际应用提供了可靠的数据支持，证明了该策略的有效性。Henn et al.[13]则通过设计启发式算法来进行订单的分批和排序，进一步减少订单的延迟时间。此外，王旭坪等[14]提出了一种旨在最小化订单处理时间的非线性拣选与配送联合调度模型，通过数值实验模拟结果分析，发现这一模型对问题的处理能力更加全面，可以应对更加复杂的拣货场景。王转[15]针对电商配送中心的实际情况，更深入地探讨了订单分批在现实场景中的应用，综合考虑拣货工具和货品包装的体积，构建了以最大化节约搬运里程为目标的订单分批求解模型。

尽管上述研究为订单分批问题提供了多种有价值的研究方法，但对于AutoStore系统，这些传统方法可能并不完全适用，仍有必要针对其特殊的储存方式和拣货方式进一步设计订单排序方法。由于该系统内单个料箱可以存储多个种类的货物，且料箱通常按照共享存储的方式紧密堆叠[16]。因此，如何有效地将多个订单组合起来，使得对同种货物有需求的订单可以尽量集中在同一个订单批次中，这对减少拣货任务分配的数量和机器人拣选料箱的次数至关重要。在现有针对AutoStore系统内货物存储问题的研究中，杨玮等[17]通过结合关联规则挖掘算法与混沌种子优化算法，提出货物合箱的存储优化方法，该方法的核心是结合关联规则挖掘算法与混沌种子优化算法。通过从机器人翻箱操作、料箱的分配规则、系统布局三方面进行分析，并结合AutoStore的运作规律，建立了以机器人拣货行走距离最短为目标的数学模型，实现了更高效的货物存储和拣货过程。吴莹莹[10]基于关联规则提出一种合箱策略，并根据FP-growth算法设计了混合种子算法进行求解。这些研究进一步丰富了针对AutoStore系统的研究内容，为研究该系统中的订单拣选策略提供了更多的可行策略选择。

然而，针对具体的AutoStore系统订单分批问题，现有文献尚未进行过系统性的方法设计。基于上述研究背景，本文以最大化单个批次内的订单相似度为目标，构建了混合整数线性规划模型求解最优订单分批策略，同时，由于订单分批问题已被证明是NP-hard问题，因此本文设计了基于层次聚类的启发式算法对大规模问题进行求解。针对不同问题规模设置了多组算例对算法进行计算实验，实验结果证明本文所提出的算法对不同规模的问题都能在短时间内求得较优可行解，证明了本文所提算法的可行性和有效性。

1 问题描述

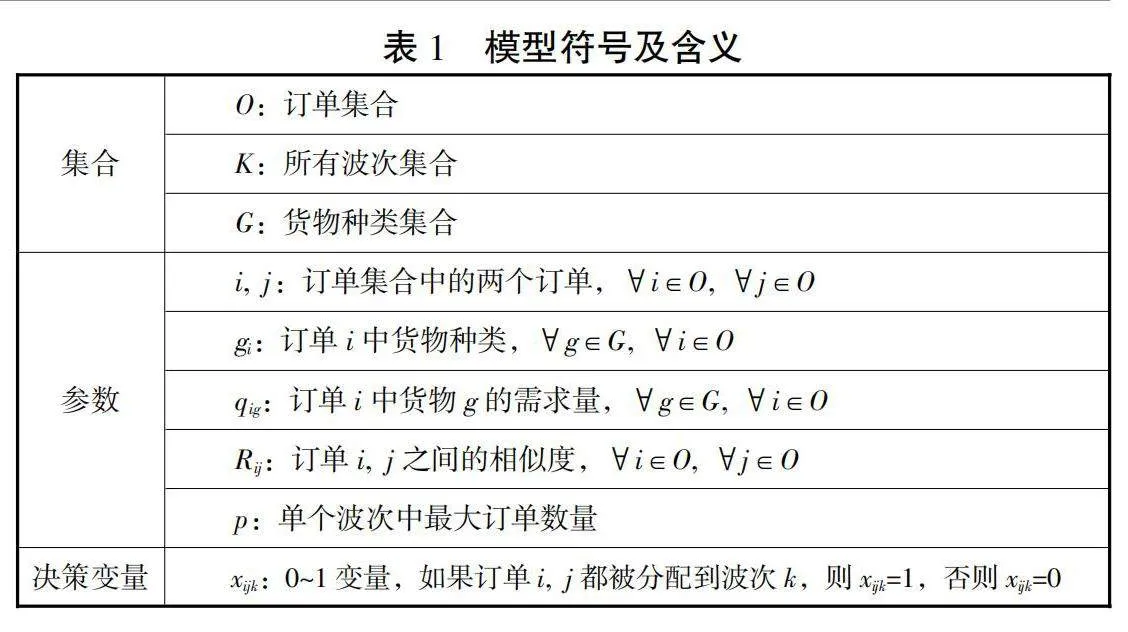
本文的问题描述为：在存有多种货物的AutoStore系统中，每个料箱中存储有m个种类货物，每个种类货物存储量为n。现需要对一批订单进行拣货，共包含O个小订单，每个订单共包含G个货物种类，每个种类需求q个货物。现在需要将这一批订单分为多个波次安排拣货指令，每个波次的分批依据为订单相似度R，即不同订单包含的相同种类货品数量；以订单i， j为例，q代表订单种类k的货物数量，那么订单间的相似度为：

式（1）说明了相似度的计算公式，即对两个订单中同时包含的货物种类而言，总需求数量较小的即为这两组订单间的相似度。本文目标是使具有高相似度的订单被分配在相同波次内，即最大化同一订单波次内相同种类货物的数量，从而将尽可能少地检索相同种类货物，提高系统拣货效率。

2 组合优化模型

2.1 问题假设。为构建模型作如下假设：（1）所有订单都具有相同的重要性，不考虑优先处理某些订单；（2）同一订单不能拆分；（3）已知各料箱中的货品信息，包括货物种类和各种类存货数量；（4）仓库里货品数量充足，不考虑补货。

2.2 模型构建。本文模型中的符号和含义如表1所示，以W为目标函数值，旨在最大化同一订单波次内相同种类货物的数量，据此建立如下混合整数线性规划模型：

式（3）表示每个订单只能被分配一次；式（4）表示每个波次订单数不超过最大订单数量；式（5）规定了变量的取值范围。

3 算法设计

3.1 算法思想。订单排序问题已被证明为NP-hard问题，为了对该问题进行快速求解，本文基于层次聚类算法，以最大化单个批次内的订单相似度为目标设计了启发式算法HC，旨在缩小搜索空间并更快地求得近似最优解。

层次聚类是一种无需预先指定聚类数量的聚类算法，它通过将数据点逐步合并成聚类簇来生成层次化的聚类结构。该算法的基本运行方式为：在算法开始时，每个数据点都被视为一个单独的簇。随后基于某种相似度度量，将最相似的两个簇合并为一个簇。这个过程会一直重复，直到所有数据点最终合并为一个簇或满足某些其他的终止条件。

3.2 算法规则

3.2.1 解的编码方式。本文使用字典对每个订单编码，包括订单编号、货物种类数、每个种类的货品数量，例如一个编号为2，包含两个货物种类的订单为：

'ID'：3， 'items'： 2：1， 5：3 （6）

式（6）表示了一个编号为“3”，包含1个种类“2”货物、3个种类“5”货物的订单。

在目标解中将所有订单构成一个订单列表，包含所有订单的编号，例如：

0，1，3， 2，4 （7）

式（7）中描述了一组将五个订单分为两个波次的解，其中：编号为0，1，3的三个订单为一个波次，编号为2，4的两个订单为另一个波次。

3.2.2 算法流程。算法的完整求解过程如下：

Step1：初始化数据。初始化订单数据，生成一批包含G个货物种类的初始订单，包括O个订单，每个订单有g个货物种类，每个种类需求q个货物。初始化簇。

Step2：计算关联矩阵。根据订单之间的相似度，计算出一个关联矩阵R。其中R表示第i个订单和第j个订单之间的相似度。

Step3：计算距离矩阵。根据关联矩阵R计算距离矩阵D，D中的每个元素表示簇之间的距离。距离矩阵初始化为最大关联值减去关联矩阵R，并将对角线元素设置为正无穷。

Step4：迭代合并簇。找到距离矩阵D中距离最近的两个簇，然后将它们合并成一个簇。删除被合并的第二个簇。更新距离矩阵D，删除对应的行和列。重复以上步骤，不断减少簇的数量，如果某次合并操作会导致某个聚类的大小超过P，则该次合并会被跳过，直到达到停止条件，即总的簇数量不大于最大波次数K，且每个波次中订单数量不超过最大订单数P。

Step5：输出结果。输出合并后的簇列表，这些簇即为分批后的各批次所包含订单。

4 数值实验

为了测试模型对不同规模大小订单的性能表现，本文利用Python3.10调用Gurobi求解器对模型进行求解，在Windows11的环境中运行，计算机配置Intel Core i7-12700H@2.30GHz，RAM16.0GB。

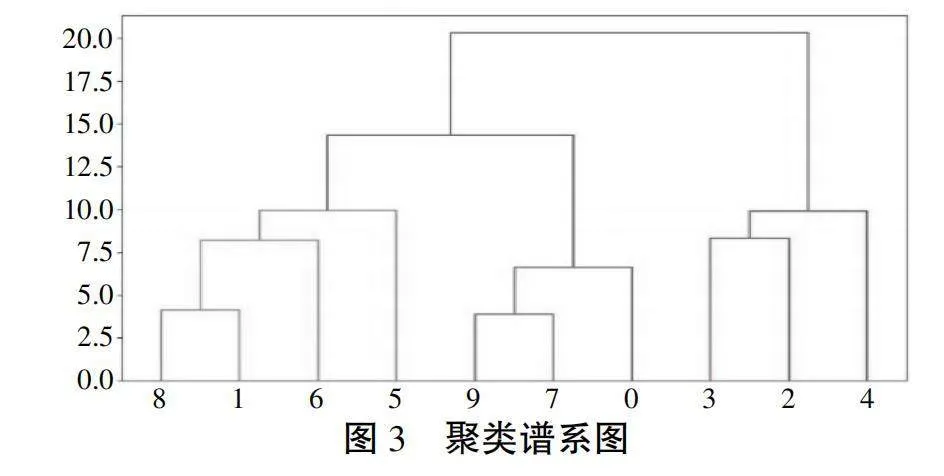
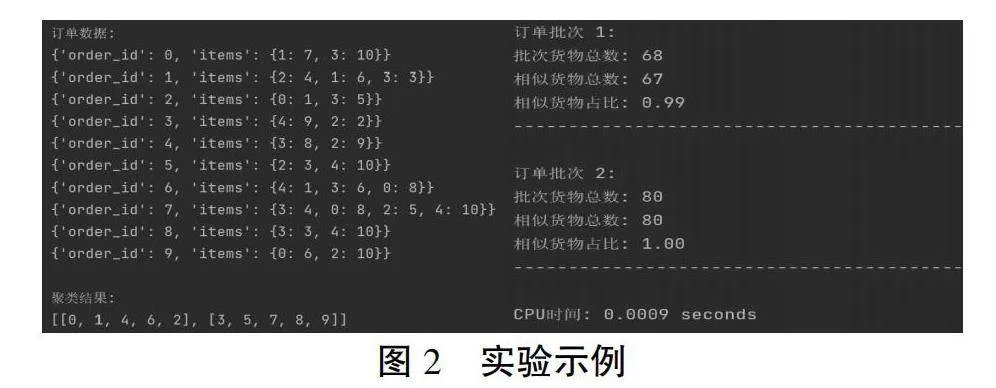
4.1 实验示例。如图2所示，以一组共包含5个种类的10个订单为例。其中每个订单包含g个种类货物，符合均值为2的几何分布；每个种类需求q个货物，q为1到10间的随机值，共分为两个订单批次。图3绘制了该问题的聚类谱系图。

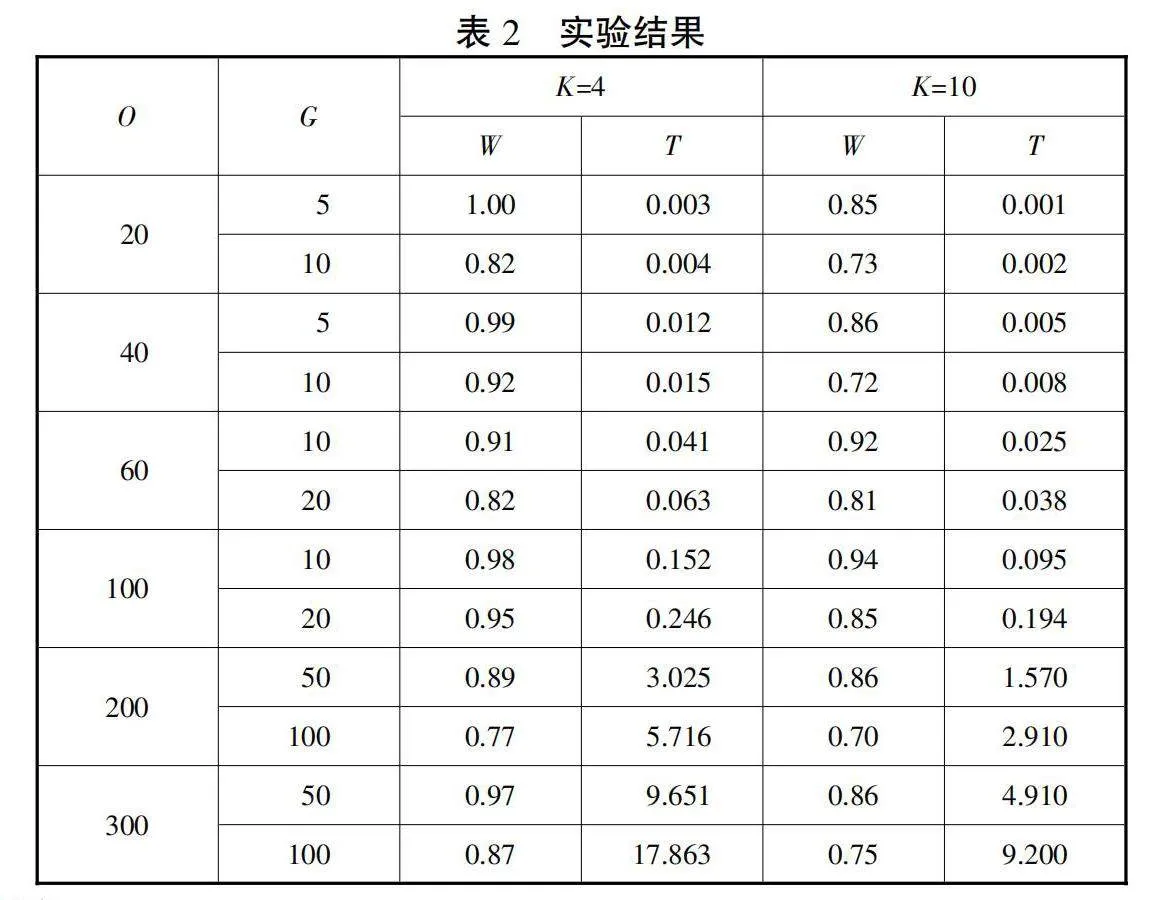
4.2 实验结果。对不同规模的算例求解结果如表2所示。标题中O表示总订单数量，G表示总货物种类数，K表示订单波次数，W表示单个订单波次内相同种类货物数量平均所占总货物数量的比值，T表示CPU计算时间（单位：秒）。

实验结果显示，对于所有参数组合，HC均能在短时间内求出可行解。对于同等规模订单算例而言，针对不同订单分批数，订单分批数越多，每个订单波次内相同种类货物数量平均所占总货物数量的比值W越低，但CPU计算时间也能得到明显降低。对于相同分批次数而言，W值并不单纯随着订单数量增大和包含货物种类数量增多而产生明显变化，仅仅与总货物种类数和订单总数的比值有关。观察数据可知，当订单所分批次和订单数量一定时，随着总货物种类数和订单总数的比值增加，W值不断降低，CPU计算时间不断增加。

因此，从最大化单个批次内订单相似度的角度而言，为了最大化同一订单波次内相同种类货物的数量，将订单进行较少的分批是更好的决策。但是，在分批数较多的情况下，每个订单波次也能有至少70%的订单相似度，且求解时间大大降低，对于更大规模的订单综合考虑，将订单进行较多的分批也是一种可行策略。

5 结 论

本文旨在研究AutoStore系统中的订单分批问题，以最大化单个批次内的订单相似度为目标，设计了混合整数线性规划模型，并设计了基于层次聚类算法的启发式算法HC。为验证算法的实用性和有效性，本文设计了一系列不同规模的算例针对所提出的算法进行实验。实验结果表明，无论是小规模还是大规模的问题，算法HC总能在短时间内求得较优可行解。结果发现在分批数一定时，订单相似度并不单纯与订单规模大小有关，主要与货物种类的总数与货物数量之间的比率有关。当订单规模固定时，选择较小的分批数量可以进一步提高订单之间的相似度。

综上所述，本文为AutoStore系统的订单分批问题提出了一种新的订单分批策略，并设计了一种能在短时间内求得较优解的启发式算法，该算法在各种规模的问题上都有出色的表现，为现实场景中的订单调度提供了新的参考方案。然而，本文仍有一定的局限性，由于在研究问题时为方便求解对问题做出了一定的简化，忽略了一些实际操作中可能存在的约束，例如订单的优先级和完成时间限制。未来的研究可以在本文研究基础上加入这些限制条件，使问题更加接近实际的操作场景，从而进一步提高算法在现实应用中的适应性和准确性。

参考文献：

[1] 周济. 智能制造——“中国制造2025”的主攻方向[J]. 中国机械工程，2015，26（17）：12.

[2] XU L D， XU E L， LI L. Industry 4.0： State of the art and future trends[J]. International Journal of Production Research， 2018，56（8）：2941-2962.

[3] BOYSEN N， DE KOSTER R， WEIDINGER F. Warehousing in the e-commerce era： A survey[J]. European Journal of Operational Research， 2019，277（2）：396-411.

[4] M W PVL. An in-depth review of automated split case picking technology for distribution centers[EB/OL]. （2019）[2023-09-05]. https：//mwpvl.com/html/swisslong autostore veview.html.

[5] BECKSCHÄFER M， MALBERG S， TIERNEY K， et al. Simulating storage policies for an automated grid-based warehouse system[C] // Computational Logistics： 8th International Conference， ICCL 2017， Southampton， UK， October 18-20， 2017， Proceedings 8， 2017：468-482.

[6] SWISSLOG. AutoStore： Space saving storage and order picking system for small parts[EB/OL]. （2021）[2023-09-05]. https：

//www.swisslog.com/en-us/products-systems-solutions/asrs-automated-storage-retrieval-systems/autostore-integrator.

[7] WINKELHAUS S， ZHANG M， GROSSE E H. Hybrid order picking： A simulation model of a joint manual and autonomous order picking system[J]. Computers Industrial Engineering， 2022，167：107981.

[8] BOYSEN N， BRISKORN D， EMDE S. Parts-to-picker based order processing in a rack-moving mobile robots environment[J]. European Journal of Operational Research， 2017，262（2）：550-562.

[9] XIE L， THIEME N， KRENZLER R， et al. Introducing split orders and optimizing operational policies in robotic mobile fulfillment systems[J]. European Journal of Operational Research， 2021，288（1）：80-97.

[10] 吴莹莹. AutoStore系统优化调度研究[D]. 西安：陕西科技大学，2021.

[11] SWISSLOG. 瑞仕格AutoStore落户上海为智慧用水打造物流之枢[J]. 现代制造，2021（11）：2.

[12] PETERSEN C G， AASE G J I J O P E. A comparison of picking， storage， and routing policies in manual order picking[J]. Production Economics， 2004，92（1）：11-19.

[13] HENN S， SCHMID V J C， ENGINEERING I. Metaheuristics for order batching and sequencing in manual order picking systems[J]. Computers & Industrial Engineering， 2013，66（2）：338-351.

[14] 王旭坪，张珺，易彩玉. B2C电子商务环境下订单拣选与配送联合调度优化[J]. 中国管理科学，2016，24（7）：101-109.

[15] 王转，裴泽平. 启发式路径下节约里程的订单分批算法[J]. 计算机工程与应用，2018，54（8）：203-209.

[16] ZOU B P， DE KOSTER R， XU X H. Operating policies in robotic compact storage and retrieval systems[J]. Transportation Science， 2018，52（4）：788-811.

[17] 杨玮，张子涵，张晓楠，等. 新型无人仓AutoStore的货物合箱方法研究[J]. 包装工程，2022，43（17）：174-183.