基于组合预测模型的上海物流需求预测

摘 要：随着物流行业的快速发展，为保证资源配置的合理运用，提前预测地区的物流货运量情况必不可少。以上海为例，将灰色预测模型与三次指数平滑预测模型结合起来，利用方差倒数加权法得到系数，再根据上海2016年到2020年实际货运量建立组合预测模型，从而预测出上海未来十年的货运量。最终发现上海货运量呈现逐年增长趋势，并在2032年达到最高

444 543.15万吨。最后，依据预测的结果对上海物流发展提供一些建议。

关键词：物流需求；灰色预测模型；三次指数平滑预测模型；组合预测模型

中图分类号：F272 文献标志码：A DOI：10.13714/j.cnki.1002-3100.2024.19.006

Abstract： With the rapid development of the logistics industry， it is essential to predict the logistics freight volume of the region in advance to ensure the reasonable utilization of resource allocation. Taking Shanghai as an example， the grey prediction model is combined with the cubic exponential smoothing prediction model， and the coefficient is obtained using the inverse variance weighting method. Then， a combination prediction model is established based on the actual freight volume of Shanghai from 2016 to 2020， in order to predict the freight volume of Shanghai in the next decade. Finally， it was found that the freight volume in Shanghai showed an increasing trend year by year， reaching a maximum of 444 543.15 million tons in 2032. Finally， based on the predicted results， provide some suggestions for the development of logistics in Shanghai.

Key words： logistics demand; grey prediction model; triple exponential smoothing prediction model; combination prediction model

0 引 言

随着世界经济的全球化，大都市在国际经济竞争与合作中发挥着越来越重要的作用[1]，上海是中国的直辖市之一，其每年的生产总值和GDP位于我国各城市的前列。随着世界经济的发展，我国港口发展迅速，港口的规模、数量和吞吐量都有了显著提高[2]。其国际航运和集装箱吞吐量也位于国际前列，在最近几年，上海港的集装箱吞吐量逐年增加，甚至超过了四千万的标准箱程度，在国际上是各国难以望其项背的程度。可以看出上海在中国的重要地位，其经济实力和地理位置对物流行业都有不小的影响。国家的经济发展是国家管理中最重要的任务。创造有利的经营和发展条件，可以在市场经济中吸引更多的投资[3]。

物流业已成为我国的基础性和支柱性产业，是国民经济发展不可或缺的支撑力量[4]。物流需求是制造与经营活动所产生的一种次生需求，它与社会经济活动紧密相关[5]。物流预测是进行物流管理的基础和前提[6]。为了能够在疫情之后快速的恢复物流行业的秩序，对接下来上海物流货运量进行预测是必须的。可靠的预测结果能够让物流的供给和需求更加平衡，使更多的社会资源涌入物流服务行业，从而使上海的经济情况能保持良好发展的状态。对于上海的物流需求预测同样可以让政府对物流行业的发展有更加系统和有效的规划，避免对有限资源的浪费。

1 单一预测方法

1.1 数据收集

首先，根据以往学者对相关预测问题的研究，本文对物流货运量进行预测的指标选择为上海地区的总计货运量。本文选用2013—2020年的上海总计货运量作为预测的参考数据。具体的货运量如图1所示。

1.2 灰色预测模型

GM1，1是目前比较常用的一种灰色模型（Grey Model），是进行灰色预测的基础，该模型最初由邓聚龙教授提出，后经广大学者的研究推广，现已广泛应用于国民经济的各个领域[7]。其优点是不需要较多的历史数据，因此本文选择上海2013—2020年货运量作为历史数据，来预测上海未来十年的货运量，模型建立步骤如下：

（1）首先，设定上海货运量序列：X=X1，X2，X3，…，Xn=84 304.63，89 979.96，90 893.00，…，138 839.00

式中：X为原始数据，Xn为第n个原始数据。

（2）根据公式X=Xn+Xn-1作一次累加得到累加数列：X=X1，X2，X3，…，Xn=84 304.63，174 284.59，180 872.96，…，259 962.99

式中：X1=X1=84 304.63。

（3）构建矩阵B和向量Y：B==Y=X2，X3，…，Xn=89 979.96，90 893.00，…，138 839.00

（4）用最小二乘法得到系数a和u：P==

式中：a为发展系数，u为灰色作用量。

（5）建立上海物流需求GM1，1模型：i+1=1-e+84 304.63+869 680.704 8e-869 680.704 8i+1=i+1-i

式中：i+1为预测值，i=1，2，3，…，n-1。

综上所述，将计算得到的各数值归纳如表1所示。

（6）对得到的GM1，1模型进行精度检验，根据已有数据得到其残差和相对误差，如表2所示。

模型相对误差值最大值0.102 1<0.2，意味着模型拟合效果达到要求。计算出均方差比值C和小误差概率P值，经计算该模型均方差比值C=0.100 5<0.35，小误差概率P=1>0.95，根据精度等级参照表，该模型为优，具有高精准度。

（7）对GM1，1模型进行适用性检验。该模型中-a=0.081 3<0.3，该模型可用于中长期预测。

1.3 三次指数平滑预测模型

指数平滑法从本质上来说属于一种特殊的加权移动平均法。对于短期预测来说，该方法十分有效。指数平滑法的计算过程容易理解、便于计算，能使用到的地方很多，只要取得少量的历史数据就可以连续使用该方法。当我们之前的预测数据发生了巨大改变时，该方法还可以进行自我调节以减少突发因素的影响。指数平滑法计算量小，容易掌握，操作简单，因此广泛用于经济研究的各个领域[8]。指数平滑法分为一次指数平滑、二次指数平滑和三次指数平滑[9]。

根据表1的具体数据可以看出上海货运量总体呈现上升趋势，所以这是一个非平稳时间序列，且呈现曲线上升趋势，所以本文采用三次指数平滑法进行短期的物流需求预测。具体步骤如下：

（1）首先，我们要确定初始值S、S、S和平滑系数α的值。在此取2013年到2015年前三期总计货运量的平均值作为初始值，为方便计算保留两位小数。

S=S=S==88 392.53

得到初始值S=S=S=88 392.53。接下来确定α的值，α取值大小体现了不同年份的货运量在预测中所占的比例；合适的α取值可以使预测更加准确。本文取α的值为0.1到0.9，分别计算不同α下的预测值，结果如表3所示。

为了得到最合适的α取值，本文将引入均方误差MSE（Mean Square Error），计算出不同平滑系数α值下的均方误差大小，结果如表4所示。

根据比较MSE的大小可以得出在α=0.9时，MSE最小，所以取平滑系数α=0.9进行预测。当α=0.9时，按公式S=αX+1-αS计算出一次指数平滑值S为：S=0.9*88 323.95+1-0.9*88 392.53=88 330.81（万吨）

同理求出S=88 324.64，S=95 997.52，S=105 884.58，S=119 600.05。

（2）在计算得到一次指数平滑的数据之后，再对一次指数平滑的数据进行一次指数平滑得到二次指数平滑值。当α=0.9时，按公式S=αS+1-αS计算出二次指数平滑值S为：S=0.9*88 330.81+1-0.9*88 392.53=88 336.98（万吨）

同理求出S=88 325.87，S=95 230.36，S=1 048 199.16，S=118 121.96。

（3）计算出各指数平滑值之后，在建立三次指数平滑模型之前，分别计算出a、b和c的值。

依据公式a=3S-3S+S得到：a=3*88 330.81-3*88 336.98+88 342.54=88 324.02

同理得到a=88 323.83，a=96 841.57，a=106 987.52，a=121 123.16。

依据公式b=6-5αS-25-4αS+4-3αS得到： b=6-5*0.9*88 330.81-25-4*0.9*88 336.98+4-3*0.9*88 342.54=-91.66。同理得到b=14.16，b

=11 402.15，b=11 783.37，b=15 936.36。

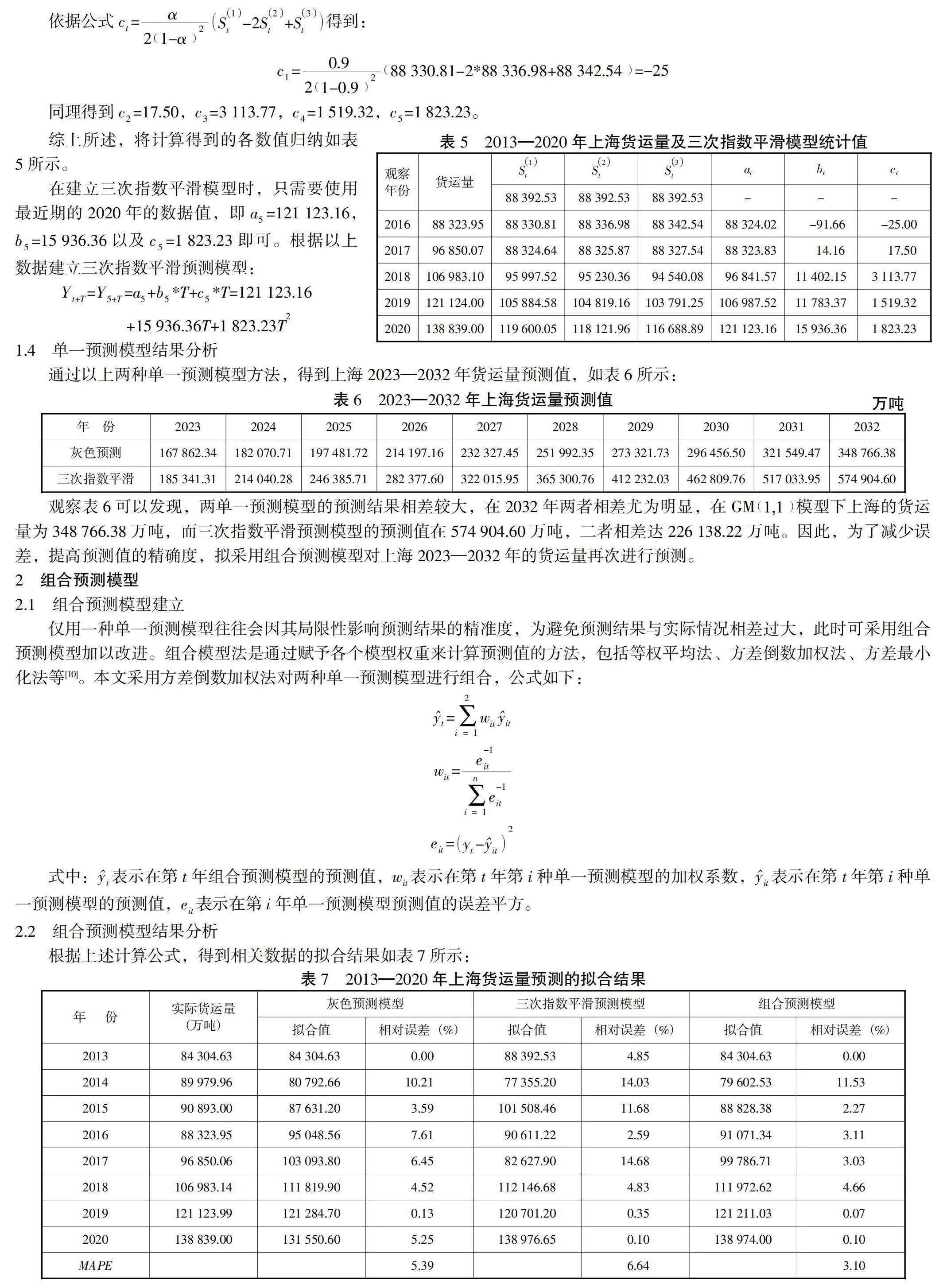
依据公式c=S-2S+S得到：c=88 330.81-2*88 336.98+88 342.54=-25

同理得到c=17.50，c=3 113.77，c=1 519.32，c=1 823.23。

综上所述，将计算得到的各数值归纳如表5所示。

在建立三次指数平滑模型时，只需要使用最近期的2020年的数据值，即a=121 123.16，b=15 936.36以及c=1 823.23即可。根据以上数据建立三次指数平滑预测模型：Y=Y=a+b*T+c*T=121 123.16 +15 936.36T+1 823.23T

1.4 单一预测模型结果分析

通过以上两种单一预测模型方法，得到上海2023—2032年货运量预测值，如表6所示：

观察表6可以发现，两单一预测模型的预测结果相差较大，在2032年两者相差尤为明显，在GM1，1模型下上海的货运量为348 766.38万吨，而三次指数平滑预测模型的预测值在574 904.60万吨，二者相差达226 138.22万吨。因此，为了减少误差，提高预测值的精确度，拟采用组合预测模型对上海2023—2032年的货运量再次进行预测。

2 组合预测模型

2.1 组合预测模型建立

仅用一种单一预测模型往往会因其局限性影响预测结果的精准度，为避免预测结果与实际情况相差过大，此时可采用组合预测模型加以改进。组合模型法是通过赋予各个模型权重来计算预测值的方法，包括等权平均法、方差倒数加权法、方差最小化法等[10]。本文采用方差倒数加权法对两种单一预测模型进行组合，公式如下：

式中：表示在第t年组合预测模型的预测值，w表示在第t年第i种单一预测模型的加权系数，表示在第t年第i种单一预测模型的预测值，e表示在第i年单一预测模型预测值的误差平方。

2.2 组合预测模型结果分析

根据上述计算公式，得到相关数据的拟合结果如表7所示：

观察可知，在灰色预测模型下，2014年货运量的相对误差最大，其值为10.21%；在三次指数平滑预测模型下，2017年货运量的相对误差最大，其值为14.68%；在组合预测模型下，2014年货运量的相对误差最大，其值为11.53%。虽然灰色预测模型的最大误差10.21%小于组合预测模型的最大误差11.53%，但组合预测模型的平均绝对百分比误差MAPE为3.1%，比灰色预测模型的5.39%和三次指数平滑预测模型的6.64%都要小。MAPE的结果越小，说明预测模型的准确度越高，由此可见，组合预测模型的准确度最高。

根据组合预测模型可得2023—2032年上海货运量预测值，如表8所示：

从表8可以看出，上海的货运量在2023—2032年呈上升趋势，在2032年达到444 543.15万吨，是2023年货运量的2.43倍。除此之外，对比2023—2032年三种预测模型的结果，分析组合预测模型预测值的稳健性，如图2所示。

从图2不难看出，不论是单一预测模型还是组合预测模型，其预测值均呈逐年增加的趋势，其中灰色预测模型的货运量预测值增长较为平缓，三次指数平滑预测模型的货运量预测值增长较快。组合预测模型的货运量预测值处于两者之间，可见组合模型下货运量预测值融合了两种单一预测模型的优点，因此，本文认为该结果符合实际。

3 结 论

本文通过组合预测模型对2023—2032年上海的货运量进行预测，通过组合预测模型可以看出上海的总货运量保持逐年递增的趋势。一方面是因为其沿海的地理位置拉动了港口经济；另一方面是其在国内和国际的经济地位，是中国连接国际的重要桥梁。所以，逐年增长的货运量符合实际情况。这对物流企业或者说是物流服务行业都是不小的压力。所以，相关企业需要提前应对，避免资源不够或者资源分配不均的情况。这时，对上海的货运量进行预测的数值发挥了重要作用。我们可以依据预测的数据来调整各种资源的分配情况，针对预测结果提出如下的建议：

（1）增加对快递进行包装和分拣的物流人员数量，以及物流末端的配送人员数量；（2）在保证货运量增加的同时，优化配送路线，学习和研究新的物流技术以提高物流的质量与效率；（3）政府可以对物流服务行业实施一些扶持性的政策，比如：减少税收，派专家对部分物流企业进行指导等；（4）政府应加强对物流行业的监督，避免浪费资源，造成无效运输，提高物流质量和效率；（5）物流服务行业应该对疫情等突发情况提高风险应对能力。

参考文献：

[1] LAN S L， YANG C， HUANG G Q. Data analysis for metropolitan economic and logistics development[J]. Advanced Engineering Informatics， 2017，32：66-76.

[2] XIE B K， ZHANG X X， LU J L， et al. Research on ecological evaluation of Shanghai port logistics based on emergy ecological footprint models[J]. Ecological Indicators， 2022，139：108916.

[3] MITROSHIN P， SHITOVA Y， SHITOV Y， et al. Big data and data mining technologies application at road transport logistics[J]. Transportation Research Procedia， 2022，61：462-466.

[4] LIANG Z J， CHIU Y， GUO Q， et al. Low-carbon logistics efficiency： Analysis on the statistical data of the logistics industry of 13 cities in Jiangsu Province， China[J]. Research in Transportation Business & Management， 2022，43：100740.

[5] 张亚晨曦. 后疫情时代湖北省物流需求预测[J]. 中国储运，2021（8）：80-82.

[6] 李明书，刘仁云，胡姝祺，等. 基于时间序列分析的长春市物流研究及预测[J]. 科技创新与应用，2020（32）：34-36.

[7] 罗永华，何忠伟. 基于灰色系统理论的茂名市物流需求预测分析[J]. 物流科技，2010，33（7）：19-21.

[8] 张祎，朱家明. 基于ARIMA和二次指数平滑模型的人口组合预测[J]. 牡丹江师范学院学报（自然科学版），2017（1）：9-12.

[9] 袁瑜，孙可朝. 国家物流枢纽货运量需求预测研究[J]. 公路交通科技，2020，37（S1）：29-34.

[10] 徐曼，陆芬. 基于组合预测模型的陕西省物流需求预测[J]. 物流科技，2023，46（11）：27-31.