无人机与卡车多组合配送问题研究

摘 要：由于城市配送场景的复杂性，无人机开始被应用于“最后一公里”配送，但无人机配送受到其飞行距离与载重等限制，无人机与卡车组合配送得到广泛关注。结合卡车与无人机配送特点，研究了一类考虑无人机与卡车多组合下的配送路径优化问题；在考虑无人机的飞行范围与载荷等因素下，建立以总配送成本最小化的整数规划模型，并设计了结合改进K-means聚类搜索的混合变邻域搜索算法求解该问题。算例结果验证了所提模型的可行性和所设计算法的有效性，通过与其他配送方式相比，成本最高节约达22%，且随着算例规模扩大，成本节约不断增加，为实现城市地区末端物流的降本增效提供了决策参考和依据。

关键词：无人机；路径规划；变邻域搜索；组合配送；城市配送

中图分类号：F252.14 文献标志码：A

DOI：10.13714/j.cnki.1002-3100.2024.19.003

Abstract： Due to the complexity of urban distribution scenarios， drones are beginning to be applied to the "last kilometer" distribution， but drone distribution is limited by its flight range and load， so the combination of drones and trucks for distribution has gained wide attention. Combining the characteristics of truck and UAV delivery， a delivery path optimization problem considering multiple combinations of UAVs and trucks is investigated. Under the consideration of the flight range and load of UAVs， an integer planning model is established to minimize the total delivery cost， and a hybrid variable neighborhood search algorithm combined with improved K-means clustering search is designed to solve the problem. The results verify the feasibility of the proposed model and the validity of the designed algorithm， and the cost saving is up to 22% compared with other distribution methods， and the cost saving increases with the expansion of the scale of the example， which provides decision-making references and bases for the realization of cost reduction and efficiency of the terminal logistics in urban areas.

Key words： UAV; path planning; variable neighborhood search; combinatorial distribution; urban distribution

0 引 言

随着无人机技术越来越成熟与规范，无人机配送受到了学界和业界的广泛关注。但无人机存在负载小、航程短等不足，这导致无人机难以较好地满足物流运输的需求。结合车辆的远距离和大容量特点与无人机的高效率和低成本，可以采用无人机和车辆组合配送的方式。这种组合配送能够满足城市复杂场景下各种类型的配送需求，并提高总体效率，同时满足安全配送的要求。因此，研究无人机和货车联合配送具有重要的理论意义和实践价值[1-2]。

车辆与无人机组合配送可理解为旅行商问题与车辆路径问题的扩展。同时根据无人机与车辆的数量可细分为使用单无人机的旅行商问题（Traveling Salesman Problem with a Drone，TSP-D）与使用多无人机车辆路径问题（Vehicle Routing Problem with Drones，VRP-D）。Kang et al.[3]根据无人机飞行特性，以总配送时间最短为目标建立整数规划模型，从而完成城市最后一公里配送任务。路世昌等[4]利用无人机与卡车协调配送对应急物流中的积水障碍问题进行研究。Agatz et al.[5]发现：与仅用卡车配送相比，小规模数量的客户使用无人机与卡车组合配送可以节省大量费用。Paul et al.[6]基于动态规划的精确方法，解决了大规模TSP-D的问题。Murray et al.[7]建立混合整数规划模型，并采取多种启发式算法求解卡车与多无人机组合配送问题。Quang et al.[2]以最小化运营成本为目标，在Murray的方法基础上，利用贪婪自适应搜索过程对无人机的配送客户点进行分配。曹英英等[8]基于无人机飞行范围与载重的约束下建立混合整数模型来服务农村地区，但同样研究的问题为TSP-D问题。季金华等[9]研究在疫情封控的背景下，以交叉感染风险与配送成本最小为目标，设计启发式算法求解TSP-D问题。彭勇等[10]通过将顾客分成三类进行研究，通过规划车辆与无人机路径使总服务时间最短。

在上述研究中，主要关注单无人机与卡车组合配送的TSP-D问题。然而，在实际配送中，由于客户点数量过多以及总需求量超过单一卡车额定载荷的限制，这种方案存在限制。因此，学者们将TSP-D问题扩展为VRP-D问题，以解决实际配送中的挑战。

Wang et al.[11]以总配送时间最短为目标，将TSP-D问题扩展为VRP-D，无人机可以从卡车或配送中心起飞。Gu et al.[12]在推广VRP-D问题的同时，将取货与送货问题融合考虑，考虑了无人机的承载能力和续航能力作为限制条件，并以最大化利润为目标，构建混合整数规划模型进行深入研究。Tamke et al.[13]针对两个不同的面向时间目标函数的带无人机的车辆路径问题（VRP-D），建立混合整数线性规划模型。

随着配送背景的复杂性增加，传统的VRP-D已经不能满足城市配送的需求。少量学者对无人机自身条件加以研究，包括无人机最大飞行时间、载重和飞行距离对续航能力的影响、道路限制对起飞点的约束等。例如，颜瑞等[14]考虑区域限制条件下卡车与无人机的组合配送。Cui et al.[15]考虑在无人机载重的约束下，提出以能耗最低为目标混合整数规划模型。但仍然存在以下几点考虑不足：（1）突发事件导致部分客户点卡车无法实现配送；（2）规定车辆必须在下一节点回收无人机；（3）配送中心周围小批量多批次的客户使用卡车进行配送，导致配送成本较高。

鉴于此，本文在考虑无人机载重、飞行距离限制、货车载重限制等约束下，无人机与货车对城市某区域内多个客户送货时，研究如何分配客户以及规划车辆和无人机路径，使配送成本最低。本文提出将独立无人机配送方式（PDTSPHqFjVcYOoPjG+CMtyylJng==）与车载无人机与卡车联合配送方式（FSTSP）相结合的无人机和卡车多组合配送（Hybrid Drone and Truck Delivery for Traveling Salesman Problem，HDTDTSP），它既能满足配送范围受限、一对一配送等特定配送需求，又能增加传统卡车配送货物的灵活性，降低整体的配送成本。

1 无人机与卡车多组合配送问题

1.1 问题描述

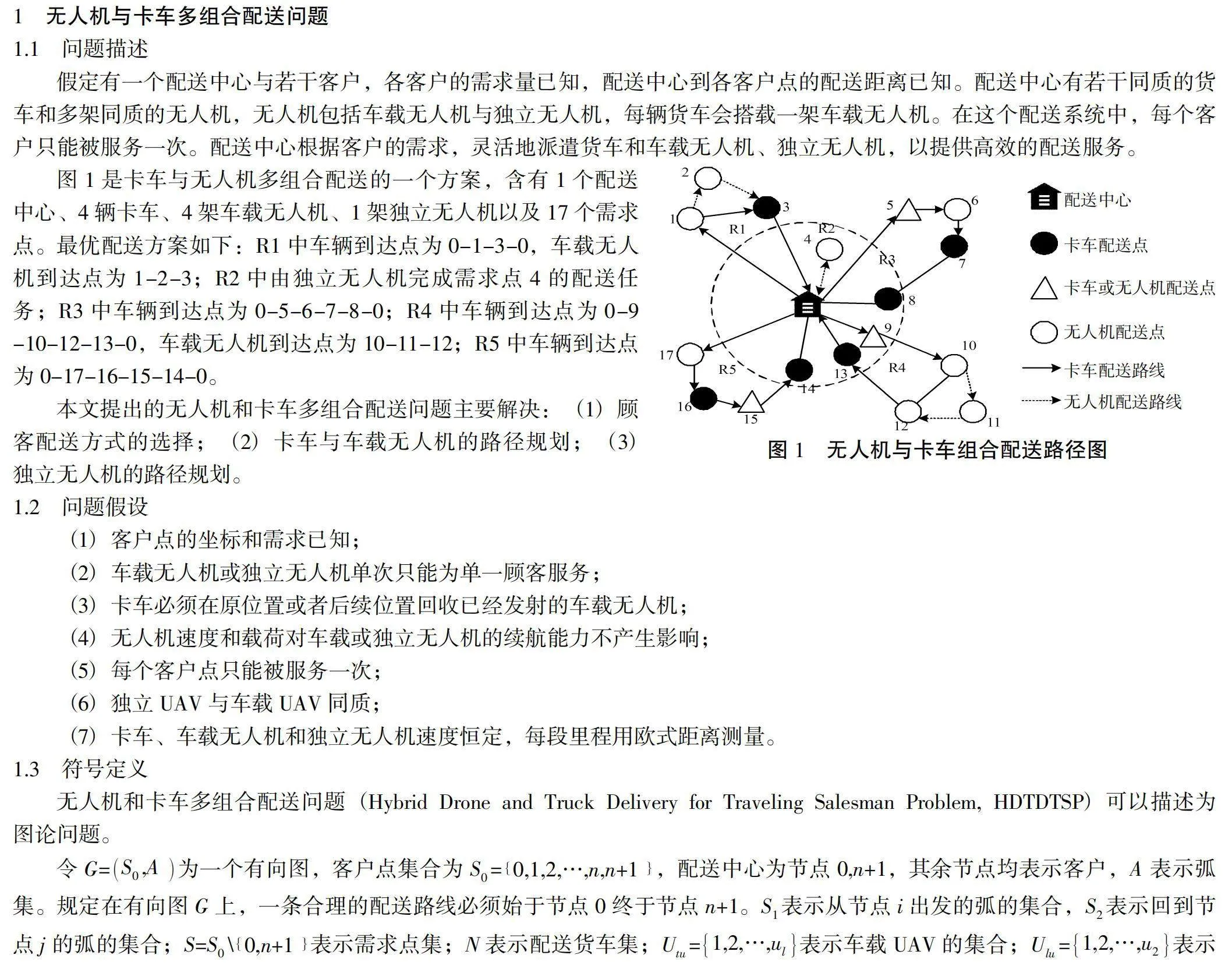
假定有一个配送中心与若干客户，各客户的需求量已知，配送中心到各客户点的配送距离已知。配送中心有若干同质的货车和多架同质的无人机，无人机包括车载无人机与独立无人机，每辆货车会搭载一架车载无人机。在这个配送系统中，每个客户只能被服务一次。配送中心根据客户的需求，灵活地派遣货车和车载无人机、独立无人机，以提供高效的配送服务。

图1是卡车与无人机多组合配送的一个方案，含有1个配送中心、4辆卡车、4架车载无人机、1架独立无人机以及17个需求点。最优配送方案如下：R1中车辆到达点为0-1-3-0，车载无人机到达点为1-2-3；R2中由独立无人机完成需求点4的配送任务；R3中车辆到达点为0-5-6-7-8-0；R4中车辆到达点为0-9-10-12-13-0，车载无人机到达点为10-11-12；R5中车辆到达点为0-17-16-15-14-0。

本文提出的无人机和卡车多组合配送问题主要解决：（1）顾客配送方式的选择；（2）卡车与车载无人机的路径规划；（3）独立无人机的路径规划。

1.2 问题假设

（1）客户点的坐标和需求已知；

（2）车载无人机或独立无人机单次只能为单一顾客服务；

（3）卡车必须在原位置或者后续位置回收已经发射的车载无人机；

（4）无人机速度和载荷对车载或独立无人机的续航能力不产生影响；

（5）每个客户点只能被服务一次；

（6）独立UAV与车载UAV同质；

（7）卡车、车载无人机和独立无人机速度恒定，每段里程用欧式距离测量。

1.3 符号定义

无人机和卡车多组合配送问题（Hybrid Drone and Truck Delivery for Traveling Salesman Problem， HDTDTSP）可以描述为图论问题。

令G=S，A为一个有向图，客户点集合为S=0，1，2，…，n，n+1，配送中心为节点0，n+1，其余节点均表示客户，A表示弧集。规定在有向图G上，一条合理的配送路线必须始于节点0终于节点n+1。S表示从节点i出发的弧的集合，S表示回到节点j的弧的集合；S=S＼0，n+1表示需求点集；N表示配送货车集；U=1，2，…，u表示车载UAV的集合；U=1，2，…，u表示独立配送UAV集合；S表示所有顾客需求点超过无人机最大载重的集合；S表示所有顾客需求点超过无人机最大续航的集合；S和S分别表示卡车和无人机的最大负载量；D表示无人机的最大续航里程；C与C分别表示卡车与无人机的单位距离配送成本；P与P分别表示卡车与无人机的单辆固定成本；w表示客户点i的需求量；e表示客户点i在卡车n路径中的序号；d表示卡车n从客户i到客户j的距离；d表示车载无人机u从客户i到客户j的距离；dd=d+d表示独立无人机u对客户i的配送距离。

1.4 数学模型

无人机和卡车多组合配送问题HDTDTSP的数学模型如下：

其中：公式（1）表示总成本最小化；公式（2）表示固定成本；公式（3）表示每辆卡车提供服务不能超过一次且不允许多次从配送中心出发；公式（4）表示卡车只有完成配送任务才允许返回配送中心；公式（5）表示卡车在完成需求点配送任务后必须离开；公式（6）表示需求点可以被卡车或者车载无人机或者独立无人机提供服务；公式（7）至公式（8）表示消除卡车路径的子回路；公式（9）至公式（10）表示若车载无人机a从点i发射，必须完成配送任务后，才可以在点k对其进行回收；公式（11）表示车载无人机的发射和回收路径必须在卡车路径上；公式（12）表示卡车的额定载重约束；公式（13）至公式（14）表示独立无人机和车载无人机的电量约束；公式（15）至公式（17）是决策变量。

2 求解HDTDTSP的变邻域搜索算法

无人机和卡车多组合配送问题HDTDTSP是比VRP更复杂的NP-hard问题，求解精确最优解的难度较大。Dhekra et al.[16]对变邻域搜索算法（Variable Neighborhood Search， VNS）改进，使其在无人机与卡车组合问题中求解效果更好。针对HDTDTSP，本文提出了一种混合变邻域搜索算法对其进行求解。

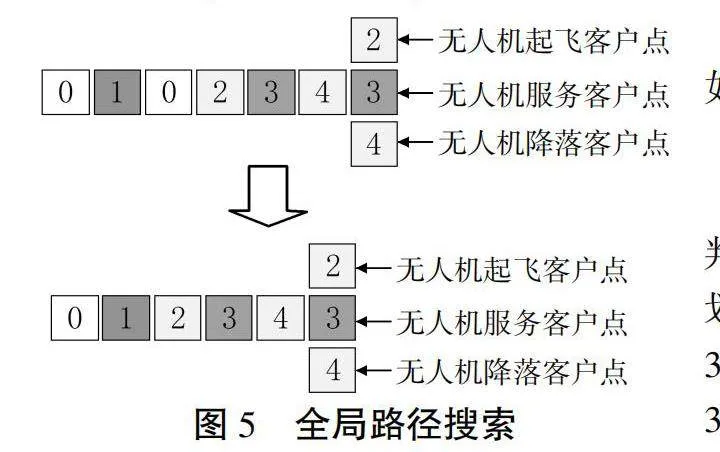
本文提出的变邻域算法主要包括四个部分：（1）顾客配送方式的选择，根据顾客的需求量以及与配送中心的距离确定顾客的初始配送方式。此外，由于每个聚类簇的配送车辆不能超过一辆，故在传统的K-means算法中加入距离和车辆载重的限制，使得聚类簇中的总需求量小于卡车的额定载荷；（2）卡车与车载无人机的路径规划，首先，根据启发式算法得到卡车与车载无人机的初始配送方案；利用领域操作对已生成的路径进行插入和交换操作，不断更新路径结果；最后，采取局部搜索操作，进一步扩大解空间，不断更新和优化路径方案；（3）独立无人机的路径规划，采用贪婪算法得到独立无人机配送方案的初始解；（4）全局最优路径搜索，交换不同配送方式的客户点，对全局路径方案进行更新。

2.1 配送方式的选择与卡车配送区域的确定

步骤1：计算所有需求点与配送中心的距离，将需求量超过独立无人机载重的需求点与距离大于独立无人机飞行半径R的需求点记录在集合P中，其余需求点放入集合N中；

步骤2：将集合P中客户点分配给卡车与车载无人机配送，集合N中客户点由独立无人机配送；

步骤3：采用手肘法确定聚类数量M；

步骤4：在客户点中随机选择M个对象作为初始聚类中心；

步骤5：计算各需求点与M个初始聚类中心的距离，在不超过卡车额定载荷的情况下，将距离最近的客户点分配至M个聚类簇中；

步骤6：根据步骤5中的M个聚类簇中心，对聚类中心信息进行更新；

步骤7：算法迭代到设定次数，计算终止，输出结果，否则转步骤5。

2.2 卡车与车载无人机路径规划

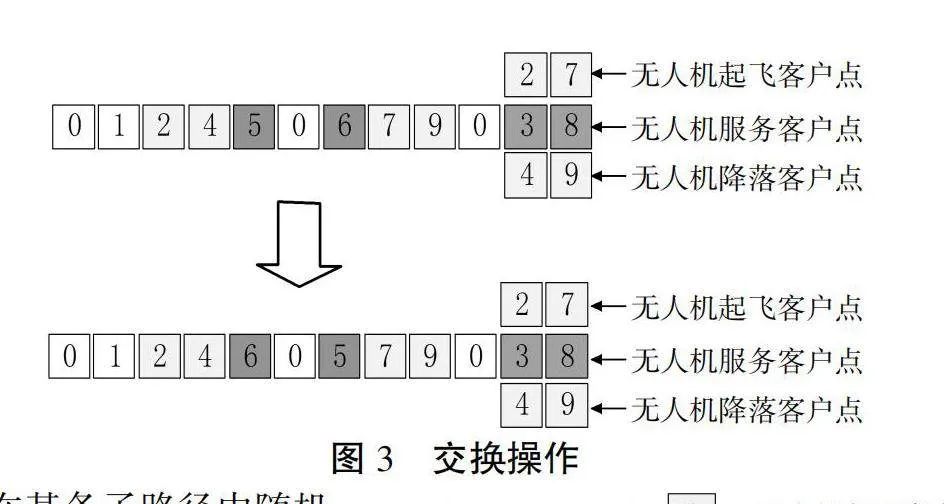
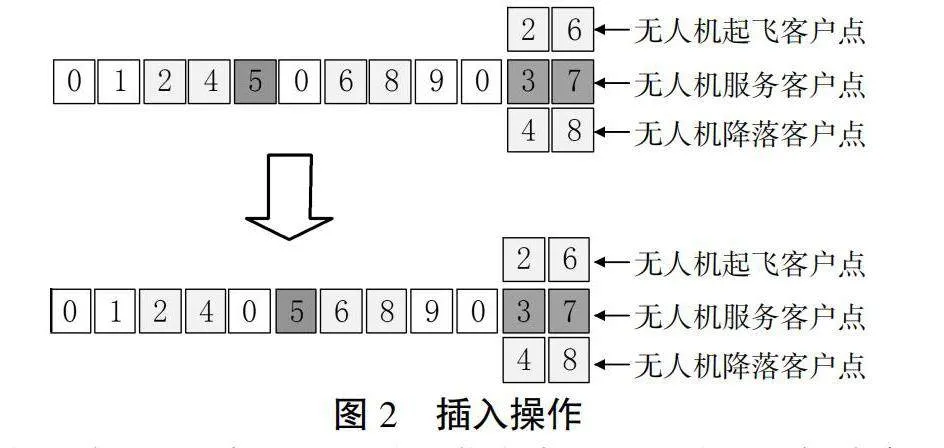
根据配送方式与聚类的结果，首先利用动态规划法得到卡车的行驶方案，然后将距离无人机配送客户点最近的两个点选为起落点，从而得到初始组合配送方案。局部搜索与插入操作、交换操作的设计可以进一步提高求解效率与精确性。如图2所示，将某路径中的某个客户插入到另一条路径中为插入操作。无人机起飞或回收点被选中时则顺延到下一点。如图3所示，交换操作是在交换后总需求量不大于卡车额定载荷前提下，对子路径中的客户点进行交替更换，若被选中的客户点为无人机的起落点，则将无人机的发射或者收回点设置为该客户点邻近点。

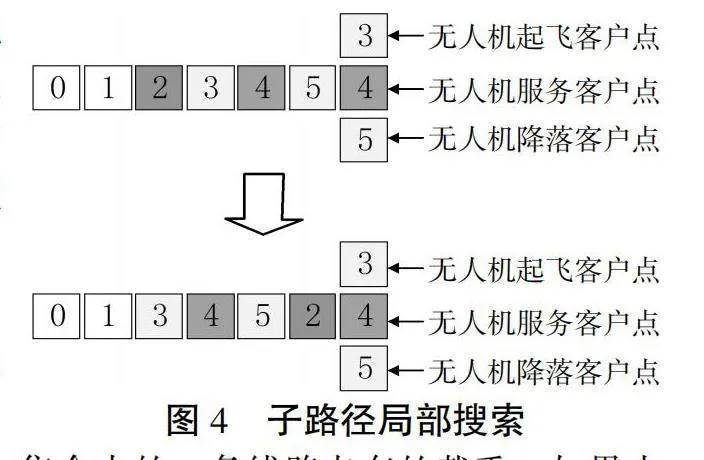
在子路径的局部过程寻找更优方案的过程就是局部搜索。即在某条子路径中随机交换两个客户点并更新路径，若被选择的客户点是无人机的发射或者收回点，则将无人机的发射或者收回点设置为该客户点邻近点，若出现无人机的发射和收回点与卡车行进方向冲突，则将发射与回收的顺序调换。路径更新的前提是原配送方案劣于新配送方案。子路径局部搜索如图4所示。

2.3 独立无人机的路径规划与全局最优路径搜索

步骤1：采取贪婪算法对集合N中的需求点进行路径规划，从而确定独立无人机的初始解；

步骤2：对圈内所有客户点进行遍历，判断客户点的需求量加入是否会超过聚类J集合中的一条线路卡车的载重，如果小于则转Step3，大于则算法结束；

步骤3：比较将客户点加入卡车配送路线增加的成本与无人机单独配送的成本，如果无人机单独配送的成本高于加入卡车路线的成本则将其加入集合M，否则跳过；

步骤4：对集合M中客户节约的成本进行计算，将其从大到小进行排列；

步骤5：依次将步骤4中客户按节约的成本高低加入卡车路线中，在加入的同时判断是否满足卡车的载重，满足则加入，不满足则停止，并根据加入的客户点重新规划路径。

3 算例分析

3.1 参数说明

在VRP Web获取CVRP的相关标准算例P-n16-k8、A-n32-k5、P-n40-k5、E-n51-k5、E-n76-k8以及E-n101-k8为基础数据，并将其命名为A16、A32、A40、A51、A76、A101，基于卡车-无人机组合配送背景要求，对标准算例数据进行一定的处理，分别包含一个配送中心和16、32、40、51、76、101个客户。此外，对客户需求量进行调整，以确保车载或独立无人机可以完成配送任务。

假设无人机的额定载荷t=15kg，航行里程D=15km，卡车额定载荷T=200kg。客户到配送点的最大往返直线距离D=15km。卡车单次固定费用为80元，无人机单次固定费用为20元；卡车的单位距离成本C=1.5元/km，无人机的单位距离飞行成本C=0.3元/km[17-18]。

运行环境为Windows11操作系统，处理器为AMD Ryzen 7 6800H with Radeon Graphics@3.20GHz。

3.2 不同配送方式的总配送成本

车辆与无人机的并行配送是指车辆与无人机分别独立完成对需求点的配送；车辆与无人机的协调配送是指车辆搭载无人机，两者共同对需求点进行配送。本文提出的车辆与无人机的多组合配送是指协同和并行两种配送方式相结合的混合配送，一方面车载无人机搭载车辆共同完成配送任务，另一方面独立无人机可从配送中心直接完成配送。

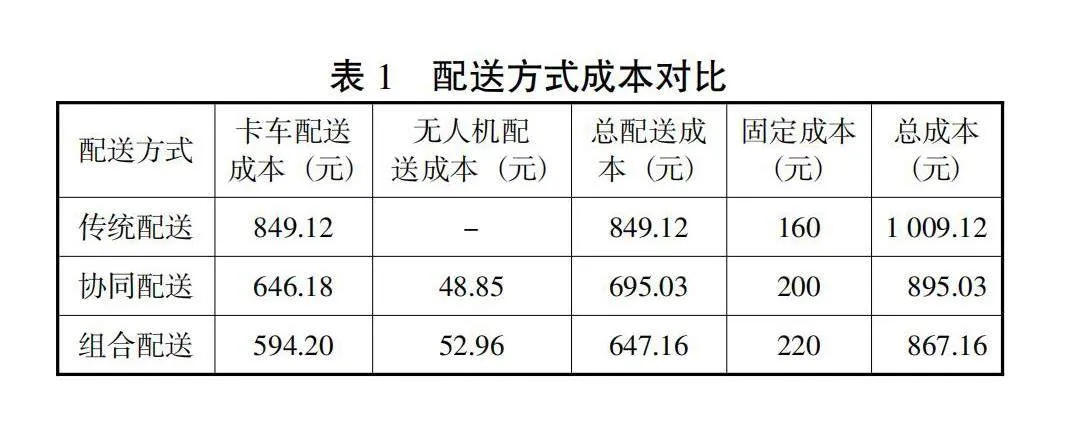
为了说明组合配送的优越性，以算例A51为例，分别采取三种配送方式进行运输，比较结果如表1所示。

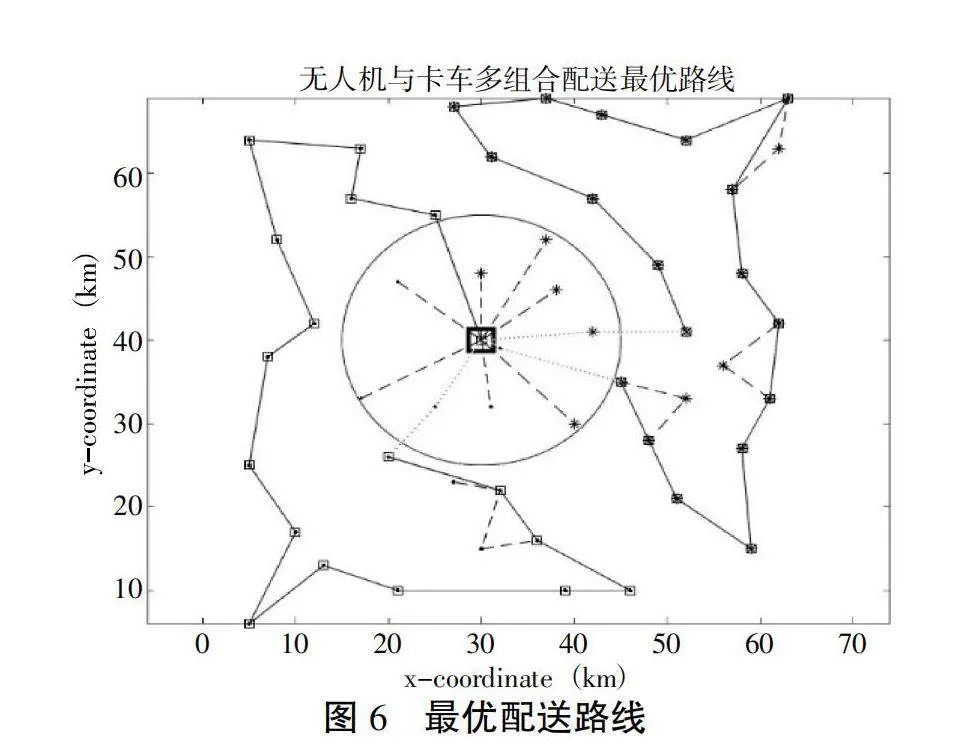
由表1可知：针对城市末端配送的复杂场景需求，结合无人机和卡车的多组合配送方式，可以同时实现协同和并行的优势。这种配送方式不仅能有效降低无人机使用频率和总配送距离，还能减少物流系统运营成本。图6为算例A51的最优配送路线。

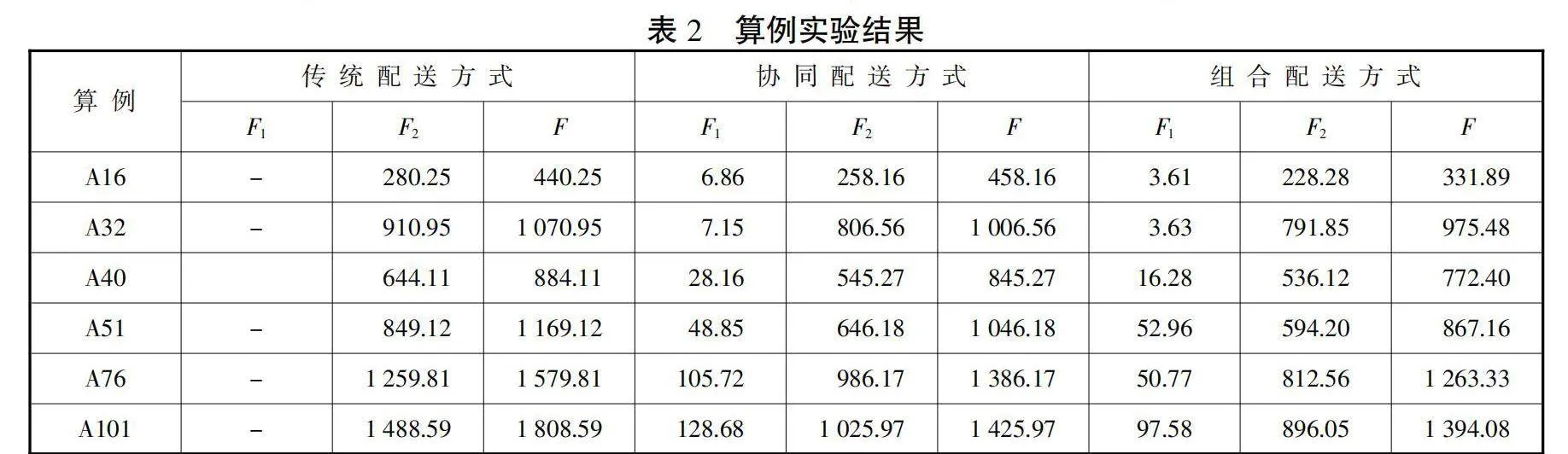
由于在最后一公里配送时经常出现交叉感染等现象，故本文考虑无人机在实施配送服务时仅对客户进行一对一配送，即车载和独立无人机单次仅配送一次客户便返回卡车或配送中心进行二次配送准备。由表2可以得出传统配送模式的固定成本占比为15.86%，但是车辆与无人机的组合配送方式在配送成本降低方面较明显，同时总成本比传统配送模式降低了12%，且随着规模的增加，成本的下降幅度更大。

3.3 算法的有效性分析

3.3.1 算法规模性分析

选取6种不同规模的数据，分别使用三种配送方式进行计算，F为无人机配送成本，F为卡车配送成本，F为运营总成本。

由表2可以看出，随着客户规模的增加，传统配送的总成本远远高于其他两种配送方式。与协同配送相比，组合配送在配送中规模的客户时总成本降低5%，在配送小规模与大规模客户，总成本降低8%。

与传统配送相比较，本文采用的组合配送由于无人机的参与，组合配送方式下的卡车里程减少近40%，且随着客户点的增加而增幅较缓。同时，为进一步对比配送方法的优劣，选取三种配送方式进行配送。经过三阶段算法优化，组合配送的总成本与传统卡车配送成本相比分别节约17.26%、12.68%、14.24%、23.78%、31.47%和33.22%，可以看出：组合配送与传统卡车相比，随着客户点规模的增多，节约的成本比例不断增加，说明该配送方法是有效的。

与并行配送相比，组合配送分别节约12.5%、2.24%、3.67%、6.89%、20.93%和13.91%。可以看出，组合配送方式与并行配送方式相比也降低了成本，进一步说明配送方法的有效性。

3.3.2 算法性能对比实验

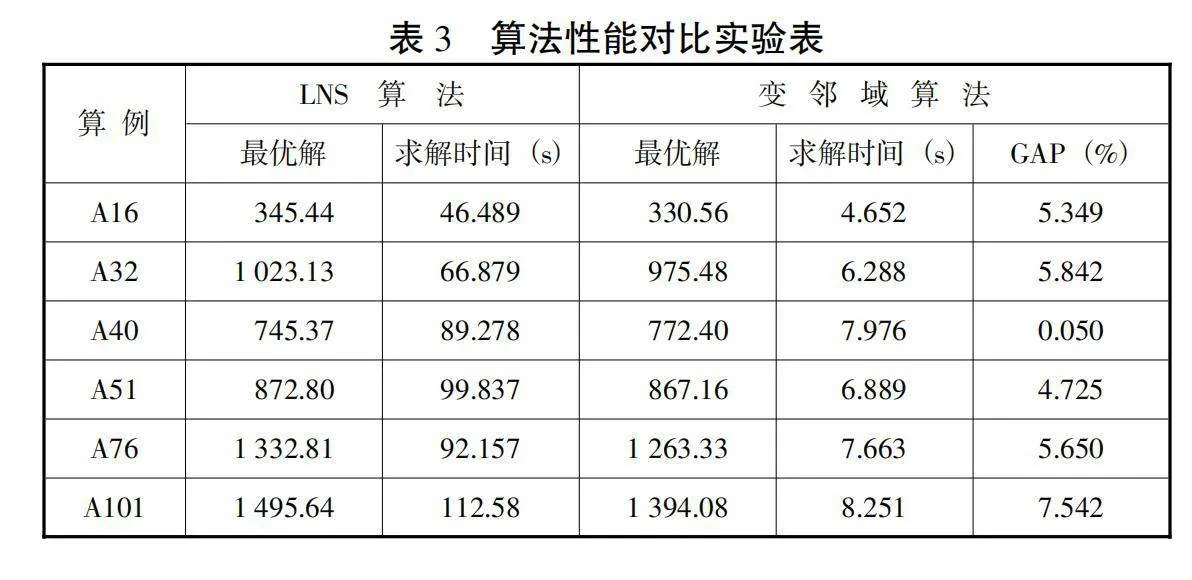
为了进一步验证变邻域算法在解决HDTDTSP问题方面的性能优势，我们选取了文献[20]中的大规模邻域搜索（LNS）作为对照。根据表3的数据，变邻域算法在解决A16、A32、A51、A76和A101这五个问题实例时，都获得了比LNS算法更优的最优解。此外，变邻域算法在求解时间方面也表现出了明显的优势，其求解时间较传统算法短得多，求解时间不到LNS算法的十分之一。同时，变邻域算法在解决表3中所列算例中的大多数最优解都优于LNS，平均差距为4.86%。综上所述，变邻域算法在解决HDTDTSP问题上显示出更高效的求解能力，能够在短时间内获得最优解决方案。

3.4 敏感性分析

3.4.1 飞行范围的敏感性分析

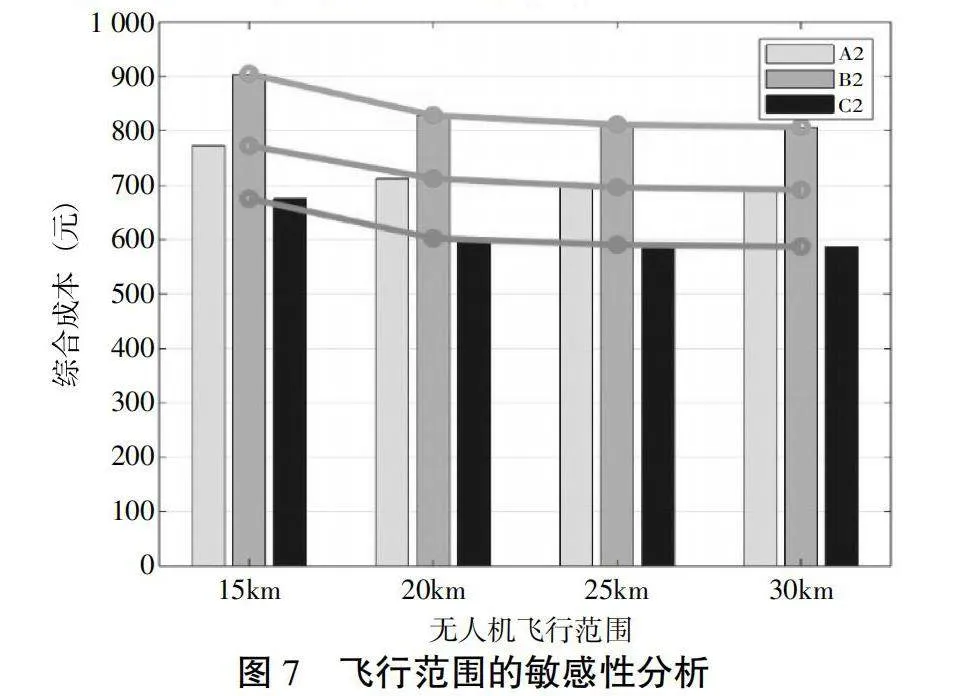
随机选择A40、A51和A76客户点数为40点的算例（即A2组、B2组和C2组），将无人机的载重设置为15kg，同时将无人机的续航能力设置分别为15km、20km、25km和30km，并进行灵敏度分析以发现飞行范围与总配送成本之间的关系。图7为A2、B2、C2三组数据的对比图，自变量为无人机的飞行范围，因变量为综合成本。

从图7可知：无人机飞行范围从15km变化至20km时，总配送成本变化明显；当飞行成本从20km增加至25km，以及从25km增加至30km时，总配送成本变动较小。在无人机飞行范围较小时，难以满足城市的配送需求，从而导致总成本变动不明显，因此在组合配送模式中发挥作用较小。但是，随着无人机飞行范围即无人机的可支配飞行空间增加，所发挥的效用也在增加，配送成本也进一步降低。当无人机的载重和飞行范围配比达到一个标准以后，飞行范围的增加并不能有效降低综合成本。

3.4.2 无人机载重的敏感性分析

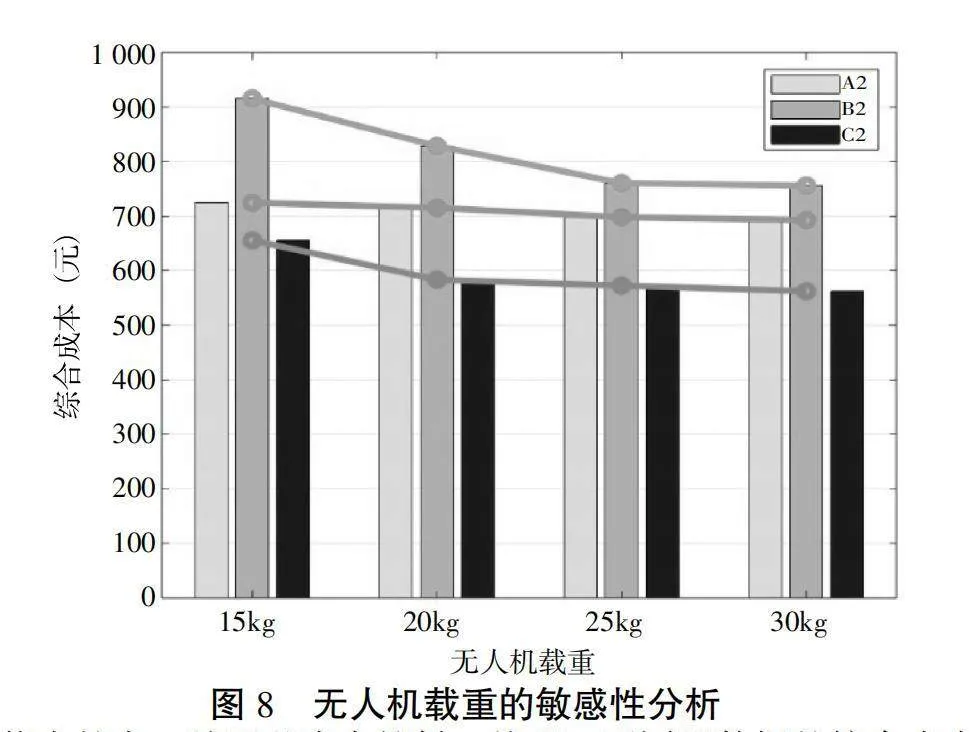
在A40、A51和A76中随机选择客户数为40的算例，设置无人机的飞行范围为15km，同时将无人机的载荷能力分别设置为15kg、20kg、25kg和30kg，并进行灵敏度分析以发现不同载重范围对总配送成本的影响。图8为三个数据集的求解结果，纵轴为总配送成本，横轴为无人机载荷能力。

从图8可知：在无人机的载荷能力等差变动的情况下，载荷能力越大，总配送成本越低。然而，不同组数据的综合成本变动范围和变动间隔存在差异。A2组的客户需求量大多集中在15kg～30kg，同时由于飞行范围的限制，综合成本变动较小，并且细微的变动主要集中在15kg～25kg之间。对于C2组的数据集，当无人机载荷能力在15kg～20kg范围内变动时，总配送成本变动较大。主要是因为客户点的需求量在15kg～20kg。无人机的载荷能力从25kg增加至30kg时，三组数据成本降低不明显，由于无人机飞行范围的限制，增加载重不能进一步降低配送成本。

4 结 论

本文研究了无人机与卡车多组合配送问题，以最小化配送总成本为目标建立模型，并设计了求解该问题的变邻域搜索算法，具体包括：首先，对客户的配送方式进行选择；其次，以卡车最大载荷为约束，使用K-means算法确定聚类并运用迭代最近点算法给出初始路径；最后，采用混合变邻域算法优化初始路径，最终得到总成本最低的路径方案。算例结果验证了本文所设计算法能有效求解所提问题，同时分析了无人机的飞行范围以及载重对最优方案产生影响。

考虑无人机与卡车多组合配送的实用性和有效性，接下来可进一步研究更有效的启发式算法，拓展并应用到城市地区更复杂的配送场景，考虑交通情况、时间窗等实际约束。

参考文献：

[1] 任璇，黄辉，于少伟，等. 车辆与无人机组合配送研究综述[J]. 控制与决策，2021，36（10）：2313-2327.

[2] QUANG M H， YVES D， QUANG D P， et al. On the min-cost traveling salesman problem with drone[J]. Transportation Research Part C， 2018，86：597-621.

[3] KANG M J， LEE C， et al. An exact algorithm for heterogeneous drone-truck routing problem[J]. Transportation Science， 2021，55（5）：1088-1112.

[4] 路世昌，邵旭伦，李丹. 卡车-无人机协同救灾物资避障配送问题研究[J]. 计算机工程与应用，2023，59（2）：289-298.

[5] AGATZ N， PAUL B， SCHMIDT M， et al. Optimization approaches for the traveling salesman problem with drone[J]. Transportation Science， 2018，52（4）：965-981.

[6] PUAL B， AGATZ N， SCHMIDT M， et al. Dynamic programming approaches for the traveling salesman problem with drone[J]. Networks， 2018，72（4）：528-542.

[7] MURRAY C C， RITWIK R， et al. The multiple flying sidekicks traveling salesman problem： Parcel delivery with multiple drones[J]. Transportation Research Part C， 2020，110：368-398.

[8] 曹英英，陈淮莉. 基于集群的卡车与无人机联合配送调度研究[J]. 计算机工程与应用，2022，58（11）：287-294.

[9] 季金华，刘亚君，别一鸣，等. 基于无人机与卡车协作的封控社区生活物资配送方法[J]. 交通运输系统工程与信息，2022，22（5）：264-272.

[10] 彭勇，黎元钧. 考虑疫情影响的卡车无人机协同配送路径优化[J]. 中国公路学报，2020，33（11）：73-82.

[11] WANG X Y， POIKONEN S， GOLDEN B， et al. The vehicle routing problem with drones： Several worst-case results[J]. Optimization Letters， 2017，11（4）：679-697.

[12] GU R X， LIU Y， MARK P， et al. Dynamic truck-drone routing problem for scheduled deliveries and on-demand pickups with time-related constraints[J]. Transportation Research Part C， 2023，151：1-19.

[13] TAMKE F， BUSHERU. A branch-and-cut algorithm for the vehicle routing problem with drones[J]. Transportation Research Part B， 2021，144：174-203.

[14] 颜瑞，陈立双，朱晓宁，等. 考虑区域限制的卡车搭载无人机车辆路径问题研究[J]. 中国管理科学，2022，30（5）：144-155.

[15] CUI S X， SUN Q， ZHANG Q， et al. A time-dependent vehicle routing problem for instant delivery based on memetic algorithm[Z]. 2022.

[16] DHEKRA R， JOUHAINA C S， WASSILA A M， et al. Application of a variable neighborhood search algorithm to a fleet size and mix vehicle routing problem with electric modular vehicles[J]. Computers & Industrial Engineering， 2019，130：537-550.

[17] 郭秀萍，胡运霞. 卡车与无人机联合配送模式下物流调度的优化研究[J]. 工业工程与管理，2021，26（1）：1-8.

[18] KITJACHAROENCHAI P， MIN B C， LEE S， et al. Two echelon vehicle routing problem with drones in last mile delivery[J]. International Journal of Production Economics， 2020，225：107598.