加强代数推理 发展理性思维

摘 要：通过分析2024年全国各地区中考部分涉及代数推理的试题，启发日常教学要注重学生符号抽象、推理、运算的训练，加强知识形成和应用过程的推理教学，关注代数推理的抽象性和直观性，深层构建代数推理认知进阶体系等，为进一步研究培养学生的代数推理能力提供思路.

关键词：代数推理；中考数学；命题特点

中图分类号：G633.6 文献标识码：A 文章编号：1673-8284（2024）10-0050-05

引用格式：樊允浩. 加强代数推理 发展理性思维：2024年中考代数推理试题的评析及启示［J］. 中国数学教育（初中版），2024（10）：50-54.

基金项目：安徽省教育信息技术研究课题——基于智慧课堂的初中数学精准教学实践研究（AH2019073）.

作者简介：樊允浩（1984— ），男，高级教师，主要从事初中数学教育教学研究.

《义务教育数学课程标准（2022年版）》指出，数学在形成人的理性思维、科学精神和促进个人智力发展中发挥着不可替代的作用. 初中阶段，除了在“图形与几何”领域有推理或证明的内容，在“数与代数”领域也有推理或证明的内容. 代数推理侧重数与式的运算、变形，具有一定的抽象性. 加强代数推理教学，有助于学生理解代数及其运算的意义. 综观2024年全国各地区中考数学试卷，发现加强了对学生代数推理能力的考查，突出了素养立意. 笔者结合2024年全国各地区中考数学试卷中涉及代数推理的相关试题，谈谈代数推理问题的命题特点及其教学启示.

一、代数推理试题类型

推理是思维的基本形式之一，一般可以分为演绎推理、归纳推理和类比推理. 其中，归纳推理和类比推理也可以统称为“合情推理”. 代数推理是以“数与代数”领域的知识为基础，通过演绎、归纳和类比等方式解决数学问题的过程. 本文中，将研究的代数推理问题分为合情推理问题、演绎推理问题，以及两者融合类问题.

二、典型试题评析

1. 合情推理

（1）归纳推理.

例1 （宁夏卷）观察下列等式：

第1个：1 × 2 - 2 = 22 × 0；

第2个：4 × 3 - 3 = 32 × 1；

第3个：9 × 4 - 4 = 42 × 2；

第4个：16 × 5 - 5 = 52 × 3；

……

按照以上规律，第n个等式为 .

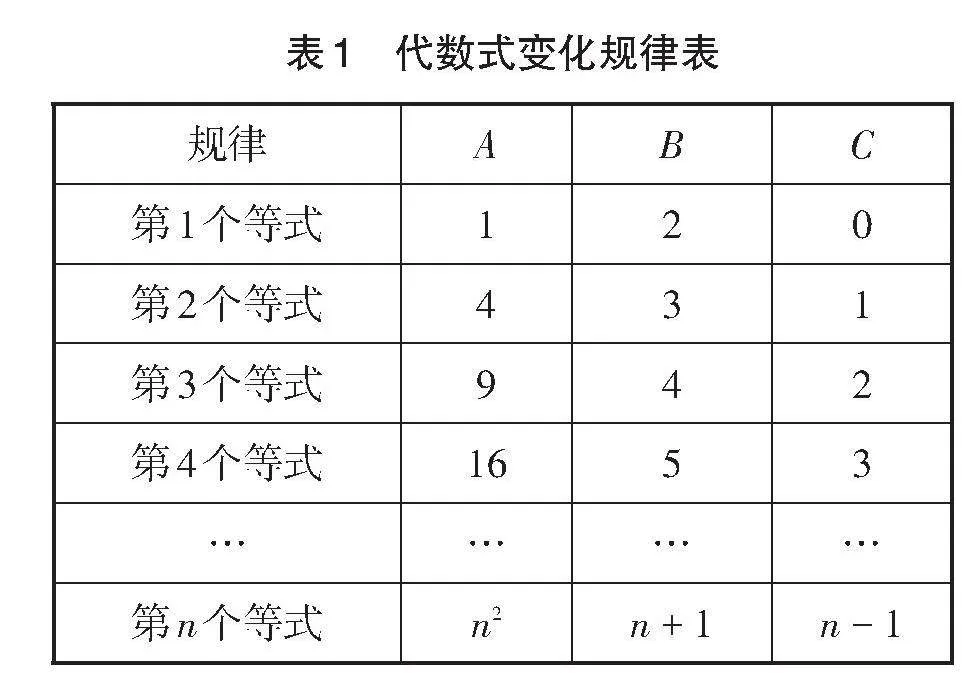
解析：该题是一道典型的数式规律题. 给出一组算式，需要学生通过观察发现等号左右两边每一项的特点及其与序数的关系. 将题干中的等式用表1的形式表示出来，发现第n个等式为n2（n + 1） - （n + 1） = （n + 1）2（n - 1）（n是正整数）.

表1 代数式变化规律表

[规律 A B C 第1个等式 1 2 0 第2个等式 4 3 1 第3个等式 9 4 2 第4个等式 16 5 3 … … … … 第n个等式 n2 n + 1 n - 1 ]

【评析】该题主要是运用归纳推理解决问题. 归纳是通过对某类事物中若干特殊情形的分析得出一般结论的思维方式. 解决此类推理题的关键是分析问题中所隐含的数量关系. 学生要学会通过观察分析几个特例，运用不完全归纳法总结出蕴含在部分对象中的共同性质，从而抽象出一般规律，用数学符号表达自己的想法. 此归纳推理是通过运算实现的，即属于代数推理.

（2）类比推理.

例2 （河北卷）“铺地锦”是我国古代一种乘法运算方法，可将多位数乘法运算转化为一位数乘法和简单的加法运算. 淇淇受其启发，设计了如图1所示的“表格算法”，图1表示132 × 23，运算结果为3 036. 图2表示一个三位数与一个两位数相乘，表格中部分数据被墨迹覆盖，根据图2中现有数据进行推断，正确的是（ ）.

<＼＼10.1.5.160＼f＼00初中＼00中数初中版2024年飞翔＼中数初中2024年第10期＼image1樊.png>[图1][图2]

（A）“20”左边的数是16

（B）“20”右边的“■”表示5

（C）运算结果小于6 000

（D）运算结果可以表示为4 100a + 1 025

解析：该题考查了整式的加法和乘法运算. 类比图1，设一个三位数与一个两位数分别为[100x+10y+z]和[10m+n]. 如图3，则[mz=20，nz=5，ny=2，nx=a].所以[m=4n]. 可以确定当[n=1，y=2]时，[m=4，z=5，]

[x=a]. 根据题意可得选项D正确.

<＼＼10.1.5.160＼f＼00初中＼00中数初中版2024年飞翔＼中数初中2024年第10期＼image8樊.png>[图3]

【评析】该题主要是运用类比推理解决问题. 先结合图1给出表示132 × 23的具体方法，计算结果为3 036，再引导学生类比这种运算方法解答问题. 解类比推理题的关键就是运用熟悉的数学知识分析未知与已有的认知结构中具有的相似特征，然后猜想其在解题方法和解题思维上的类似之处，从而解决问题. 应用类比推理解决问题可以培养学生的思维能力，让学生对问题产生更深层次的认识，从而提高解题效率. 该题是通过运算解决的，故属于代数推理.

2. 演绎推理

例3 （重庆A卷）我们规定：若一个正整数A能写成m2 - n，其中m与n都是两位数，且m与n的十位数字相同，个位数字之和为8，则称A为“方减数”，并把A分解成m2 - n的过程，称为“方减分解”. 例如，因为602 = 252 - 23，25与23的十位数字相同，个位数字5与3的和为8，所以602是“方减数”，602分解成602 = 252 - 23的过程就是“方减分解”. 按照这个规定，最小的“方减数”是 . 把一个“方减数”A进行“方减分解”，即A = m2 - n，将m放在n的左边组成一个新的四位数B，若B除以19余数为1，且2m + n = k2（k为整数），则满足条件的正整数A为 .

解析：设m = 10a + b，则n = 10a + 8 - b（1 ≤ a ≤ 9，0 ≤ b ≤ 8）. 要使“方减数”最小，需a = 1，可求得m = 10，n = 18，即最小的“方减数”是82；根据“B除以19余数为1，且2m + n = k2（k为整数）”，得出[3a+4b+719]为整数，30a + b + 8是完全平方数，由于1 ≤ a ≤ 9，0 ≤ b ≤ 8，逐个检验计算，即可求解.

【评析】该题主要是运用演绎推理来解决. 从定义出发，推出某个特殊情况下的结论. 已知新定义（大前提），并存在特殊情况（小前提），即设m = 10a + b，则n = 10a + 8 - b（1 ≤ a ≤ 9，0 ≤ b ≤ 8），且B = 1 000a + 100b + 10a + 8 - b = 1 010a + 99b + 8，利用新定义得出特殊情况下的结论. 演泽推理的基本形式为“三段论”，即“大前提—小前提—结论”. 这个过程既能培养学生自主探究的能力，又能提升学生演绎推理的能力. 学生在日常学习中要注重问题的探究过程，体验知识抽象的过程，要学会用严谨的数学语言进行表达. 以上演绎推理是通过相关运算实现的，故属于代数推理.

例4 （福建卷）已知实数[a，b，c，m，n]满足[3m+n=ba，mn=ca].

（1）求证：[b2-12ac]为非负数.

（2）若[a，b，c]均为奇数，[m，n]是否可以都为整数？说明你的理由.

解析：（1）由题意，得[b=a3m+n，c=amn]. 计算，得[b2-12ac][=a23m-n2].

由此可知[b2-12ac]是非负数.

（2）m，n不可能都为整数. 理由如下.

若m，n都为整数，其可能的情况有：① m，n都为奇数；② m，n为整数，且其中至少有一个为偶数.

① 当m，n都为奇数时，则[3m+n]必为偶数. 因为[3m+n=ba]，所以[b=a3m+n]. 因为[a]为奇数，所以[a3m+n]必为偶数. 这与[b]为奇数矛盾.

② 当m，n为整数，且其中至少有一个为偶数时，则mn必为偶数. 因为[mn=ca]，所以[c=amn]. 因为[a]为奇数，所以[amn]必为偶数. 这与[c]为奇数矛盾.

综上所述，m，n不可能都为整数.

【评析】该题主要是运用演绎推理解决问题. 数与式的运算及性质的应用都是基于数与式的性质、运算法则和运算律的演绎推理. 方程、不等式和函数实质上都是数量关系，研究数量关系主要是基于数式通性的等价变形，这种等价变形的本质也是演绎推理. 第（1）小题的解答离开演绎推理是没法进行的，考查了整式的运算、因式分解、等式的性质等基础知识，以及综合应用所学知识分析问题、解决问题的能力. 解第（2）小题时，要按照推理证明的格式写出证明过程. 该题表面看是考查学生对有关数的奇偶数性质的掌握情况，深层看是以这些知识为载体，考查学生的推理能力.

3. 合情推理与演绎推理融合

例5 （江苏·盐城卷）发现问题：

小明买菠萝时发现，通常情况下，销售员都是先削去菠萝的皮，再斜着铲去菠萝的籽.

提出问题：

销售员斜着铲去菠萝的籽，除了方便操作，是否还蕴含着什么数学道理呢？

分析问题：

某菠萝可以近似看成圆柱体，若忽略籽的体积和铲去果肉的厚度与宽度，那么籽在侧面展开图上可以看成点，每个点表示不同的籽. 该菠萝的籽在侧面展开图上呈交错规律排列，每行有n个籽，每列有k个籽，行上相邻两籽、列上相邻两籽的间距都为d（n，k均为正整数，n > k ≥ 3，d > 0），如图4所示.

<＼＼10.1.5.160＼f＼00初中＼00中数初中版2024年飞翔＼中数初中2024年第10期＼image27.png>[（a）][（b）][图4]

小明设计了如下三种铲籽方案.

方案1：图5是横向铲籽示意图，每行铲的路径长为 ，共铲 行，则铲除全部籽的路径总长为 .

<＼＼10.1.5.160＼f＼00初中＼00中数初中版2024年飞翔＼中数初中2024年第10期＼image28.png>[图5]

方案2：图6是纵向铲籽示意图，则铲除全部籽的路径总长为 .

<＼＼10.1.5.160＼f＼00初中＼00中数初中版2024年飞翔＼中数初中2024年第10期＼image28.png>[图6]

方案3：图7是销售员斜着铲籽示意图，写出该方案铲除全部籽的路径总长.

<＼＼10.1.5.160＼f＼00初中＼00中数初中版2024年飞翔＼中数初中2024年第10期＼image28.png>[图7]

解决问题：

在三个方案中，哪种方案铲籽路径总长最短？试写出比较过程，并对销售员的操作方法进行评价.

解析：对于方案1和方案2，由题意归纳出数量关系，列出代数式即可求解；对于方案3，由图7可以得出斜着铲每两个点之间的距离为[d2+d22=2d2]，根据题意得到一共有2n列、2k行籽，斜着铲相当于有n条线段长，即可得出铲除全部籽的路径总长为[22k-12]dn. 在“解决问题”阶段，利用作差法比较三种方案即可得到方案3铲籽路径总长最短. 销售员的操作方法是选择最短的路径，减少对菠萝的损耗.

【评析】该题是代数合情推理与演绎推理的融合运用. 解题时，学生需要经历由合情推理到演绎推理的代数推理全过程. 在“分析问题”阶段，需要通过观察发现三种方案中的每行籽数、行上相邻两籽的间距与每行铲的路径长，以及铲除全部籽的路径总长的数量关系，通过不完全归纳法抽象出一般规律并将其用式子表达出来，重在对归纳推理能力的考查. 在“解决问题”阶段，通过对代数式的运算，推理出方案3的铲籽路径总长最短，进而解决问题，重在对演绎推理能力的考查. 总体来说，该题通过让学生经历发现问题、提出问题、分析问题和解决问题的过程，引导学生经历由合情推理到演绎推理的代数推理全过程.

总之，基于运算的代数推理，以代数运算为基础，侧重对数与式的运算和变形，以及对运算规律的提炼与证明，具有一定的抽象性. 该题要求学生能基于具体数值运算实例归纳得到具有一般性的运算规律，用数学符号表示该规律，考查学生的归纳推理能力和演绎推理能力. 在实际解题中，为了确保归纳的正确性，学生可以依据运算法则或等式（不等式）的性质进行演绎推理，积累用数学符号进行一般性推理的经验.

三、教学启示

1. 注重对符号抽象、推理、运算的训练

代数领域的符号抽象主要体现在运用符号表示数、数量关系及其变化规律. 代数中的符号推理的特点是“基于运算”，初中阶段代数的本质特征就是符号运算，加强代数推理有助于学生理解代数及其运算的意义. 在教学中，教师可以以数与式的性质、运算及关系作为代数推理教学的出发点，引导学生基于符号运算和推演，探析和表征运算法则、规律和公式，逐步发展学生的代数推理能力. 例1中给出了一组等式，观察等式左右两边每一项的特点及其与序数的关系，要求学生推理得出第n个等式. 教师可以让学生观察：这组等式有什么特点？等式的每一项与它对应的序数有什么关系？有什么发现？在学生经过一系列观察、比较、分析、推理并给出猜想后，教师引导学生总结出一般规律并将其用字母表示出来. 教师可以进一步引导学生利用乘法公式进行证明. 加强运算、推理的教学主要是加强算法、技能背后的算理、运算律的教学，引导学生关注运算、推理的步步有序和步步有据.

2. 加强知识形成和应用过程的推理教学

日常教学中，教师要引导学生关注知识的形成过程. 在数学概念的学习过程中，需要从特殊事物的不同属性中归纳出共同的、本质的属性，形成概念的定义；能够利用概念的定义进行简单的推理. 例如，根据有理数的定义推出两个有理数的四则运算的结果仍然是有理数，利用无理数的定义判断一个数是不是无理数. 在数学法则的教学过程中，让学生经历观察、计算、归纳、类比、猜想、论证等过程，发展学生的代数推理能力. 例如，在学习完全平方公式时，教师可以给出几道数学表达式，引导学生观察、计算，发现其中蕴含的数学规律，并让学生尝试编写问题，经历“再发现”的过程，自然生成完全平方公式，再通过运算、推理确定公式的合理性. 通过以上探索，学生能体验代数推理的内涵和用途，切实提升推理能力. 同时，在知识应用过程中，教师还要引导学生反思：正在做什么（目标）？为什么要这么做（依据）？接下来该做什么（方向）？能得到什么结论？等等. 这样的反思有助于学生厘清思考过程中每一个判断的理由和依据，使思考的过程和思维的轨迹变得清晰、有条理，从而提高思维的敏捷性和深刻性，以及发现问题和提出问题、分析问题和解决问题的能力. 这正是促进代数推理能力进阶的重要方式.

3. 代数推理教学要关注抽象性和直观性

推理是数学的基本思维方式. 其中，代数推理和几何推理的侧重点不同. 代数推理注重运用代数规则和运算法则进行变形与转化，几何推理则注重观察和分析图形的性质和关系. 日常教学中，要引导学生关注代数推理与几何推理的融合，丰富学生理性思维的提升路径. 教师要认识到代数推理的抽象性是其核心特征，但过于抽象的内容容易使学生感到困惑. 因此，教师要引导学生通过直观寻求代数推理的方法，从图形（图象）出发，将图形问题代数化，将代数推理结论借助直观加以解释，使抽象性和直观性相结合，使学生逐步深入理解代数推理的本质，从而整体提升推理能力和问题解决能力.

4. 深层构建代数推理认知进阶体系

代数推理过程是逐级抽象和一般化的思维发展过程，使学生的抽象思维得到高度发展. 代数推理的认知发展由低到高分为具体化算术、结构化算术、符号化概括、形式化建构和一般化推广五级. 图8的代数推理学习进阶系统中，每一级代表学生代数推理认知发展过程中的关键点，前三级对应意识层的进阶发展，后三级对应能力层的进阶发展. 其中，符号化概括是意识层和能力层链接的桥梁，既是意识层的最高级，也是能力层的起点. 每一层级的发展都是以前一层级为基础，呈现螺旋上升式发展.

[一般化推广][辩证逻辑] [形式化建构][理性一般] [分析] [符号化概括][理性具体] [抽象] [结构化算术][感性一般] [概括] [具体化算术][感性具体] [识别] [认知进阶] [思维发展] [能力层] [意识层][图8 代数推理学习进阶系统]

加强代数推理占据“数与代数”学习领域的重要位置. 综合分析学生核心素养具体表现的认知进阶发展，可以为构建符合学生认知发展规律的学习进阶系统奠定基础. 日常教学中，教师要因材施教、循序渐进，加强代数推理教学，发展学生的理性思维.

参考文献：

［1］ 中华人民共和国教育部. 义务教育数学课程标准（2022年版）［M］. 北京：北京师范大学出版社，2022.

［2］ 王远敏. 初中代数推理的表现及应用［J］. 中学数学教学参考（中旬），2023（10）：66-68.

［3］ 史宁中，曹一鸣.《义务教育数学课程标准（2022年版）》解读［M］. 北京：北京师范大学出版社，2022.

［4］ 吕亚军. 指向数学推理能力提升的课堂教学设计：以“完全平方公式”为例［J］. 中学数学月刊，2024（6）：7-9，23.

［5］ 何勇. 例析初中数学代数推理的类型及教学启示［J］. 中学数学，2024（10）：84-85.

［6］ 吴立宝，刘颖超. 从意识到能力：代数推理认知发展的进阶理路［J］. 课程·教材·教法，2023，43（4）：120-126.