明晰作图原理 发展理性思维

摘 要：依据新课标、新教材的理念和导向，尝试改变几何作图教学中只教作图程序的现象. 以“如何用尺规作一个角等于已知角”这一典型实例为载体，重点引导学生思考“怎么想到这样画、为什么这样画”，启发学生经历深度思考的过程，发展学生的几何直观和推理能力.

关键词：尺规作角；明晰原理；理性思维

中图分类号：G633.6 文献标识码：A 文章编号：1673-8284（2024）10-0041-04

引用格式：李莎. 明晰作图原理 发展理性思维：以“尺规作角”的教学为例［J］. 中国数学教育（初中版），2024（10）：41-44.

尺规作图，即有限次地使用无刻度直尺和圆规进行作图的活动. 从古希腊欧几里得的《几何原本》开始，尺规作图就作为构建几何演绎体系的基础，也是学习与理解几何概念及其关系的基本工具.《义务教育数学课程标准（2011年版）》指出，对于尺规作图，学生不仅要知道作图的步骤，而且要知道实施这些步骤的理由.《义务教育数学课程标准（2022年版）》（以下简称《标准（2022年版）》）中增加了尺规作图的相关知识点，强调不仅要把尺规作图作为一种几何学习任务，更重要的是将它作为一种感知几何图形、理解几何概念和图形性质、探究几何规律的认知工具.

学生在小学阶段认识几何图形，是基于对图形的直观感知，在初中阶段注重用推理的方法研究几何图形. 用推理的方法所研究的几何图形，是有逻辑的直观图形——尺规作图作出的几何图形. 因此，尺规作图是用推理的方法研究几何图形的有逻辑的直观基础. 下面以“尺规作角”一课的教学为例，启发学生经历深度思考的过程，发展学生的几何直观和推理能力.

一、教学内容解析

本节课选自苏科版《义务教育教科书·数学》七年级上册“6.2 角”第2课时的第一部分，主要内容为用圆规和无刻度直尺作一个角等于已知角. 尺规作角是学生在初中阶段学习尺规作图的初步体验，其探究方法对后续开展其他尺规作图的学习具有重要的启蒙作用. 小学阶段，学生已经学习了用三角板、量角器画一些特殊角，在有关平面图形的学习中也学习了线段和角等相关概念，掌握了用圆规截取等长线段的方法. 用尺规来实现作一个角等于已知角，即“复制”一个相同的角，其本质是利用尺规作线段来确定所作角终边上的关键点，这是本节课的重点也是难点. 教学过程应立足学生的已有认知，引导学生借助已有的知识储备和学习经验，从用量角器画角的过程中寻找灵感，有逻辑地构建目标图形的示意图，再根据直观示意图的组成元素及其位置关系，执果索因，确定作图方法，进而用尺规构图作出目标图形，最后用逻辑推理证明所画图形的正确性. 从用量角器画角到用尺规作角，是学生从形象思维到抽象思维的一次重要跨越. 教学过程中应重点引导学生在观察、操作、猜想、证明等实践活动的过程中，建立直观操作与抽象作法之间的联系，培养学生的空间观念和探究性思维，发展学生的几何直观和推理能力.

二、素养导向的教学目标

基于以上分析，确定本节课的教学目标如下.

（1）经历尺规作角的过程，增强动手能力，能想象出通过尺规作角所形成的图形，发展空间观念和几何直观.

（2）理解尺规作角的基本原理与方法，发展几何直观和推理能力.

（3）经历尺规作角方法的探索过程，通过与量角器画角过程的类比、猜想，推断尺规作角的方法，初步体会尺规作图的基本思路，发展推理能力和抽象能力.

三、教学过程设计

环节1：创设情境，构建目标图形.

引言：将一条射线绕着它的端点旋转到另一个位置就形成了一个角，我们把这个角记为∠AOB. 为了进一步用推理的方法研究角，需要用圆规和没有刻度的直尺作一个角等于已知角. 那么怎样作呢？我们先从画角开始探究.

问题1：如果∠AOB = 30°，你能画一个和∠AOB一样大的角吗？

追问：如果∠AOB = 50°，你打算怎么画一个与其一样的角？∠AOB = 80°呢？

思考：你认为用量角器画角的关键是什么？

师生活动：教师先板演一个角的形成过程. 通过问题引领，学生尝试用三角板或量角器分别画出以OA为始边的30°，50°，80°角，并将三个角分别标记为∠AOB1，∠AOB2，∠AOB3. 学生经历操作、观察、分析的过程，明确画一个角的关键即确定角终边上的一个点，我们称之为确定该角的关键点.

【设计意图】基于学生的已有认知，以“如何画一个30°的角”引入课题，使学生经历用三角板、量角器画角的过程，明确画一个角的关键即确定该角终边上的一个点. 在引导学生回忆旧知的同时为后面尺规画角的教学作铺垫.

环节2：类比关联，分析目标图形.

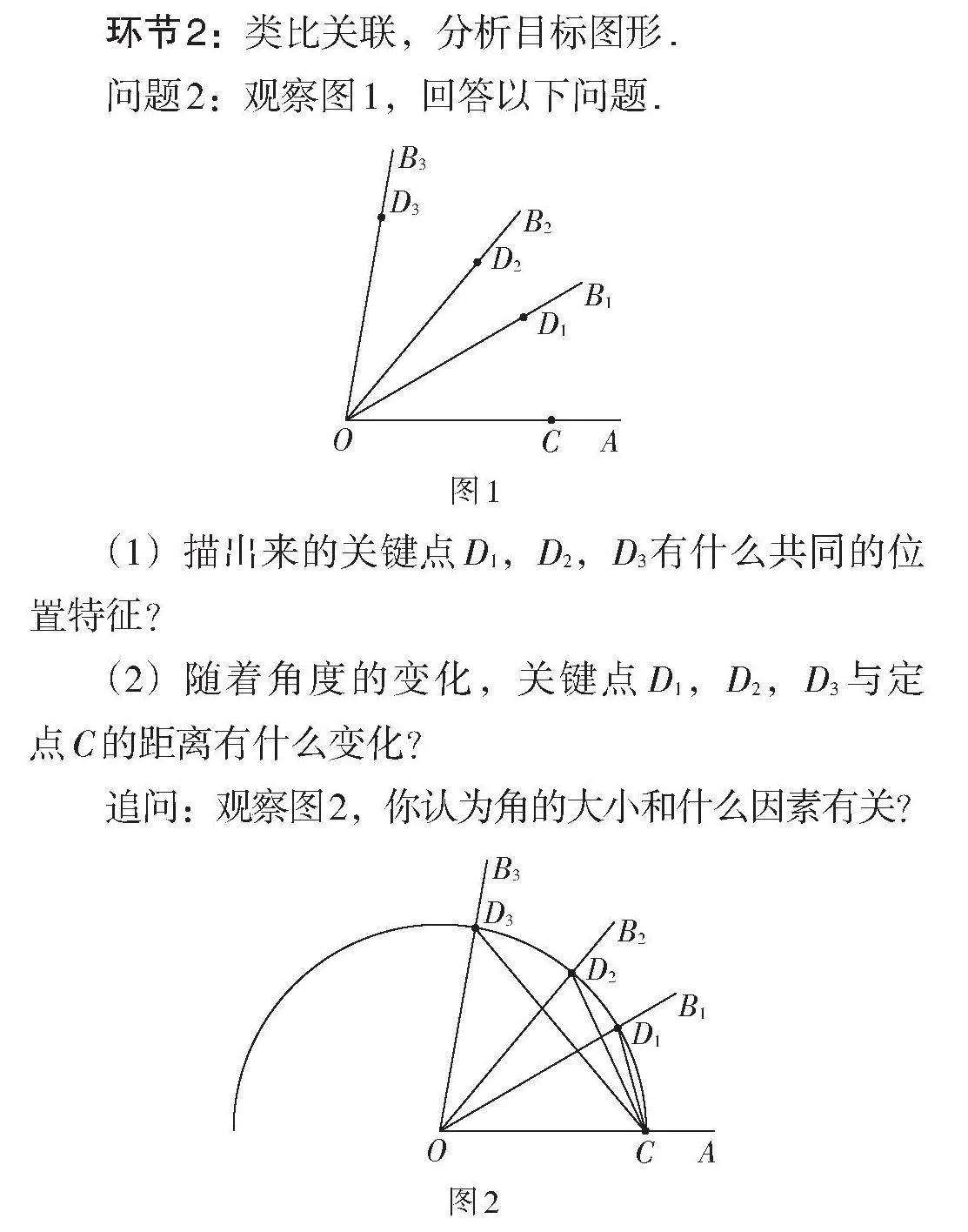
问题2：观察图1，回答以下问题.

[O][B3][B2][B1][D3][D2][D1][C][图1][A]

（1）描出来的关键点D1，D2，D3有什么共同的位置特征？

（2）随着角度的变化，关键点D1，D2，D3与定点C的距离有什么变化？

追问：观察图2，你认为角的大小和什么因素有关？

[O][B3][B2][B1][D3][D2][D1][C][图2][A]

师生活动：教师引导学生通过对图1中几个特殊角的关键点的观察，得到一般猜想，即决定一个角大小的关键点具有共同的位置特征. 它们都在量角器的边缘弧上. 如果把量角器的边缘弧看成以中心O为圆心，OC长为半径的半圆，则关键点到圆心O的距离相等，即OD1 = OD2 = OD3 = OC. 教师继续用教具展示同一条圆弧上角的变化过程，通过问题引领，学生观察发现：同一条圆弧上，关键点D（动点）与点C（定点）的距离随着角度的变化而变化. 同一条圆弧上，一个角的大小由该圆弧上C，D两点的距离（线段CD的长）确定.

【设计意图】引领学生经历同一圆弧上确定角的大小的关键因素的探究过程，将新旧知识有效衔接，逐步突破教学难点. 探究过程渗透了由特殊到一般的数学思想，注重引导学生通过有逻辑地构建直观图形来关注事物的共性，进而得到作图方法.

环节3：执果索因，拟订作图方法.

问题3：如图3，如何利用尺规画∠A′O′B3′，使∠A′O′B3′ = ∠AOB3？

[O][B3][D3][C][图3][A]

追问1：要“复制”一个和∠AOB3一样的角，我们可以先任意画一条射线O′A′作为始边. 通过前面的分析，我们得到画一个角的关键就是确定该角终边上的一个点，那么这个关键点D3′在哪里呢？如何“复制”一个和图3同样大小的圆弧呢？

师生活动：学生借助圆规“复制”和图3同样大小的圆弧，即以点O′为圆心，OC长为半径画圆弧，从而得到关键点D3′所在的第一条圆弧.

追问2：此时点D3′一定在这个圆弧上. 那么圆弧上的哪一点表示点D3′呢？设所画圆弧与射线O′A′的交点为点C′，那么所画角的大小还与什么有关？如何“复制”一条和线段CD3等长的线段呢？

师生活动：学生借助圆规“复制”和CD3等长的线段，即以点C′为圆心，CD3长为半径画弧，从而得到关键点D3′所在的第二条圆弧. 通过两条弧的交点确定关键点D3′，最后过点D3′画射线O′B3′，作出∠A′O′B3′（如图4）.

[O′][B3′][D3′][C′][图4][A′]

追问3：在画∠A′O′B3′的过程中，圆规和直尺分别发挥了怎样的作用？

师生活动：学生回忆作角过程中直尺和圆规的作用，体会尺规作角的方法.

【设计意图】立足已有的用量角器画角的学习经验，让学生初步尝试将尺规作角转化为通过尺规作线段来实现，使学生经历用尺规作等角的探索过程，体会用尺规作等角的方法，发展学生的几何直观和推理能力.

环节4：尺规构图，作出目标图形.

问题4：如图5，已知∠AOB，如何用尺规作∠A′O′B′，使∠A′O′B′ = ∠AOB？

[O][B][A][图5]

追问1：现在没有了圆弧，该怎么办？圆弧的大小对角的大小有影响吗？说说你的看法？

追问2：所作角与已知角是否相等？如何验证？

师生活动：从“有弧”到“无弧”，学生经历了再思考的过程. 教师引导学生作出圆弧后，将问题4的解决自然转化为问题3，引导学生经历尺规作角的完整操作过程. 在教师问题的引领下，全班学生交流展示. 学生或用量角器测量，或将所画角与已知角进行叠合来验证尺规作角的准确性，同时直观感受圆弧大小的任意性及尺规作角的科学性.

追问3：说一说用尺规作一个角等于已知角的步骤.

师生活动：全班交流、优化作图痕迹，师生共同得出用尺规作一个角等于已知角的步骤.

归纳作法如下.

（1）如图6，以点O为圆心，任意长为半径画弧，分别交OA，OB于点C，D；

（2）画射线O′A′，以点O′为圆心，OC长为半径画弧，交O′A′于点C′；

（3）以点C′为圆心，CD长为半径画弧tNPF1ocB1T4gU3ufYJ/dhnlBHf0EBkPbD10KAA6eSFQ=，交前弧于点D′；

（4）过点D′作射线O′B′.

则∠A′O′B′即为所求.

[O′][B′][D′][C′][A′] [图6] [O][B][D][C][A] [（a）][（b）]

【设计意图】从问题3到问题4，从“有形”到“无形”，学生经历了从具体形象思维到抽象思维的跨越，思维活动渐次提升. 通过画角、验角等操作，培养了学生的动手能力、科学态度和理性精神.

环节5：论证说理，抽象作图本质.

问题5：如图7，连接CD，C′D′，想一想△OCD和△O′C′D′的三边有怎样的数量关系？说一说你的理由.

[O′][B′][D′][C′][A′] [图7] [O][B][D][C][A] [（a）][（b）]

师生活动：通过构造如图7所示的三角形，教师引导学生明晰尺规作角方法的实质. 学生或叠合△OCD和△O′C′D，或根据尺规作角的过程进行推理，得出两个三角形的三边关系，即O′C′ = OC = O′D′ = OD，C′D′ = CD，抽象出化角为线的方法.

【设计意图】引导学生对尺规作角的作法进行口头说理论证，抽象化角为线的方法，发展学生的推理能力和抽象能力.

四、教学思考

与传统思考问题的方式相比，尺规作图更多的是培养学生的几何直观和逆向思维. 教师在教学中要注重引导学生主动用通性通法探究尺规作图的方法，并对作出的图形进行说理论证. 在分析和解决问题的过程中，培养学生的数学思维能力，发展空间观念、几何直观和推理能力.

1. 加强通法指导，形成整体思维

《标准（2022年版）》中要求的19种尺规作图在作图方法的本质、内容的联系性上体现了数学的整体性. 在尺规作图的教学中，教师应加强学法有章可循的通法指导，帮助学生形成尺规作图一般化的思维习惯和探究思路，使学生在获得数学基础知识和基本技能的过程中，领悟基本思想，积累基本活动经验. 首先，教师应引导学生通过对问题进行分析，使学生明确“已知什么，要作什么”，并根据问题给出的条件构建直观图形，然后借助已有的学习经验和知识储备思考该怎么作，并根据图形的性质及图形间的联系，通过推理找出画图的方法，进而作出目标图形，最后通过说理正向证明所作图形的正确性. 例如，本课例中，用尺规作一个角等于已知角时，可以先确定角的始边，即借助直尺任意画一条射线，然后思考“该怎样确定角的终边”. 通过对用量角器画角过程的分析得出画一个角的实质，即确定该角终边上的一个关键点，执果索因，得出尺规作角的方法，最后说理证明所作角的正确性.

2. 注重过程实践，发展学科素养

《标准（2022年版）》指出，要经历尺规作图的过程，增强动手能力，能想象出通过尺规作图的操作所形成的图形，理解尺规作图的基本原理与方法，发展空间观念和空间想象力. 依据新课标、新教材的设计理念和导向，教师应改变目前几何作图程序性教学的做法，不能仅限于让学生掌握具体作法，更重要的是让学生充分经历作图方法探析的过程，让学生在直观操作与抽象作法之间建立联系，感悟两者相互依存的关系，发展学生的几何直观和推理能力. 例如，本课例中，教师引导学生在用量角器量角、画角的活动中寻找灵感，使抽象问题具体化，引导学生经历观察、操作、猜想、推理等实践活动，得出确定一个角终边关键点的方法，使教学难点得以突破，进而完成尺规作角. 教师因势利导，以问题引领学生观察所构建的三角形的三边关系，使学生再次经历思维过程，抽象得出化角为线的方法，明晰尺规作角的本质.

在尺规教学的过程中，教师应加强对学生的学法指导，注重“教思维”，让学生在自主探究的过程中进一步发展所必需的数学基础知识、基本技能、基本思想和基本活动经验，形成解决尺规作图问题的基本方法和策略，在遇到新的情境和新的问题时，可以迁移应用，发展数学核心素养；在面对现实生活情境时，会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界.

参考文献：

［1］欧几里得. 几何原本［M］. 燕晓东，译. 南京：江苏人民出版社，2011.

［2］中华人民共和国教育部. 义务教育数学课程标准（2022年版）［M］. 北京：北京师范大学出版社，2022.

［3］吴增生. 用整体教学追求直观与逻辑的融合发展：ICME-14中国特色主题活动中“平行线的判定与性质”课例研究［J］. 中国数学教育（初中版），2021（9）：11-17.

［4］骆文娟. 从《原本》与“课标”谈尺规作图教学［J］. 数学通报，2022，61（12）：17-21.

作者简介：李莎（1986— ），女，中学一级教师，主要从事初中数学教育教学研究.