学习进阶视角下项目式学习的实践与思考

摘 要：综合与实践活动是培养学生综合运用知识和方法解决实际问题能力的重要载体. 以“包装纸盒的设计”为项目主题，借助具有挑战性和开放性的驱动性问题，营造一个开放且有意义的探究空间，阐述基于学习进阶理论的数学项目式学习的实践与思考．

关键词：包装纸盒设计；项目式学习；数学核心素养

中图分类号：G633.6 文献标识码：A 文章编号：1673-8284（2024）10-0009-07

引用格式：许笑笑，黄信永. 学习进阶视角下项目式学习的实践与思考：以“包装纸盒的设计”为例［J］. 中国数学教育（初中版），2024（10）：9-15.

《义务教育数学课程标准（2022年版）》（以下简称《标准》）提出，初中阶段综合与实践领域，可采用项目式学习的方式，以问题解决为导向，整合数学与其他学科的知识和思想方法，让学生从数学的角度观察与分析、思考与表达、解决与阐释社会生活以及科学技术中遇到的现实问题. 由此可见，项目式学习是课程深化和时代发展的需求. 以“包装纸盒的设计”为主题，赋予学生“包装纸盒设计师”的角色，以项目学习任务群为主线落实数学核心素养的发展.

一、对学习进阶的理解

在《标准》中，“进阶”一词共出现了4次，主要聚焦于学习目标进阶、知识进阶和核心素养进阶. 基于学习进阶理论的初中数学项目式学习旨在揭示学生在学习和探索某一主题时，对该主题的思考和理解，以及实践活动经验在相当长一段时间内是如何从简单到复杂、从低水平到高水平、从新手到专家逐渐发展的，以提升学生的数学核心素养为重点，强调学习思维的递进.“学习进阶”包含6个基本要素，如表1所示.

表1 学习进阶的6个要素

[要素 内容 进阶起点 在学生开始学习和探究某一内容或实践前具备的实际水平 进阶终点 学习进阶的最高水平（顶点），是某一阶段学习结束时期望学生达到的学科理解能力 进阶维度 学科内或科学实践过程中的核心概念，通过追踪学生在这些维度上的水平可以了解其整体学习进程 进阶水平 指在学习进阶所追踪的发展路径上存在多个相互关联的中间步骤，这些步骤反映了学生思维发展过程的普遍阶段 学业表现 指处于特定理解水平的学生在完成某类任务时所应有的表现 学业测评 用于追踪学生在预期进阶路径上的发展情况 ]

二、项目主题的确定

在确定项目主题的过程中，需要考虑问题背景、核心知识、学生学情等因素，基于此建立项目式学习与学科文化、数学元素及人文社会的广泛联系. 项目主题是项目式学习活动开展的“心脏”，涉及一个待解决的实际问题和对学生具有一定挑战性的驱动性问题.《标准》指出，让学生借助折叠纸盒等活动经验，认识立体图形展开图，建立立体图形与展开后的平面图形之间的联系，培养空间观念和空间想象能力. 因此，“包装纸盒的设计”项目重点探究如何在给定材料的情况下，设计、绘制出一个容积尽可能大的包装纸盒.

三、基于学习进阶理论的项目实施过程

1. 进阶起点

由表2可知，“包装纸盒的设计”与第三学段和第四学段的核心知识具有紧密联系.

表2 学生的学习进阶起点（知识储备）

[学段 核心知识 《标准》要求 第三学段 展开图 借助折叠纸盒等活动经验，认识立体图形展开图，培养空间观念和空间想象能力 第四学段 二元一次方程组 能根据二元一次方程组的特征，选择代入消元法或加减消元法解二元一次方程组 等腰三角形

直角三角形 探索并掌握等腰三角形、直角三角形的性质定理和判定定理 一元二次方程 能用配方法、公式法、因式分解法解数字系数的一元二次方程 相似三角形 了解相似三角形的性质定理和判定定理 展开图 能根据展开图想象和制作模型；通过实例，了解展开图在现实生活中的应用 ]

该项目是以初中数学核心知识为基点，在学生学完立体图形的展开图之后，开展的综合与实践活动. 此时，学生具备了一定的发现与提出问题、分析与解决问题的能力，拥有一定的应用意识、创新意识和实践能力，初步掌握了问题解决的基本步骤，为项目程序的开展奠定了基础.

2. 进阶终点

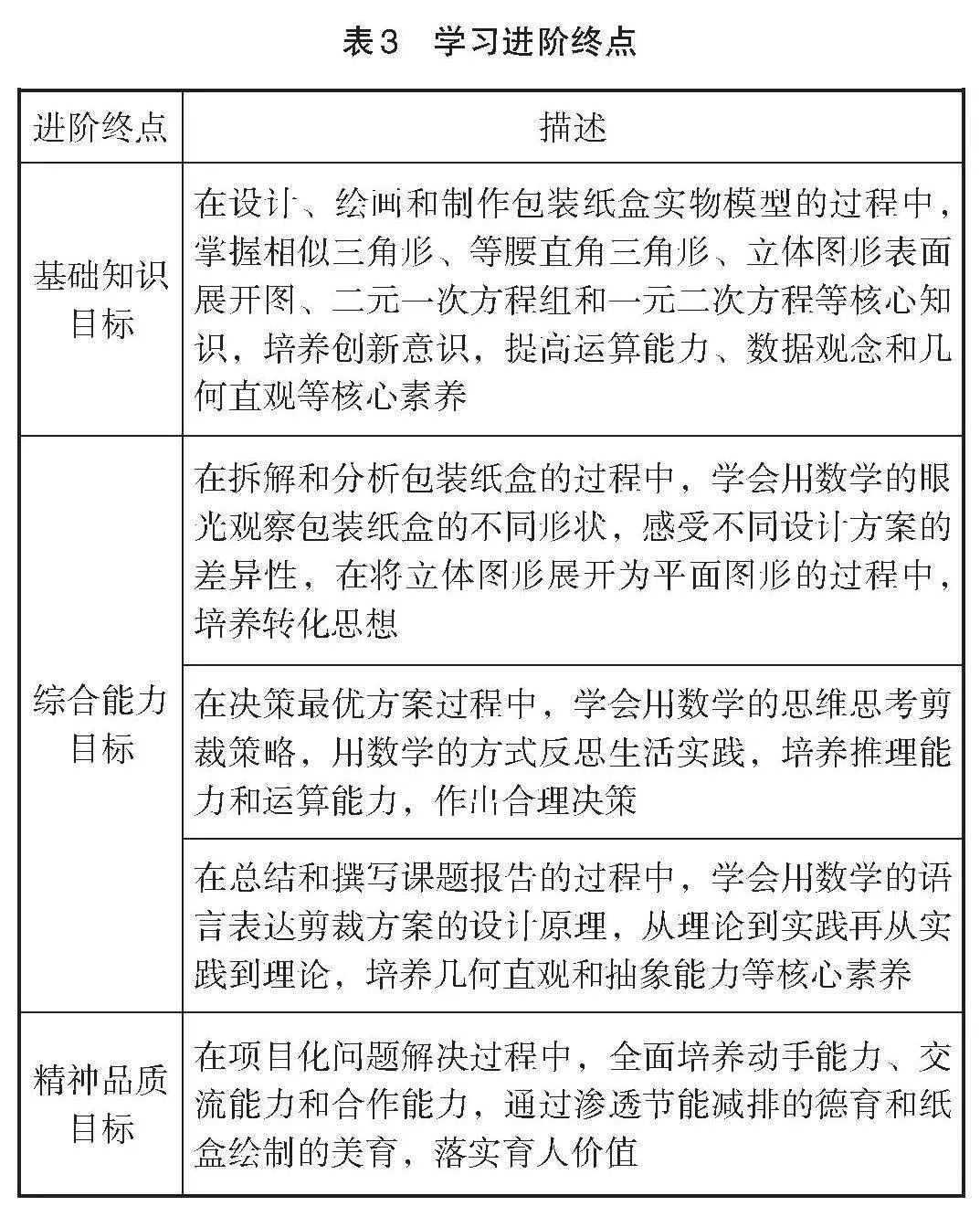
包装纸盒在生活中随处可见，其中蕴含着数学、科学、美学等学科知识. 因此，设计包装纸盒具有丰富的价值和意义. 基于数学核心素养导向，教学目标自始至终统领着项目程序的设定、项目活动的组织、项目过程的优化和项目质量的评价. 根据布卢姆的教育目标分类法，给出学习进阶终点的三个目标——基础知识目标、综合能力目标和精神品质目标，如表3所示.

表3 学习进阶终点

[进阶终点 描述 基础知识目标 在设计、绘画和制作包装纸盒实物模型的过程中，掌握相似三角形、等腰直角三角形、立体图形表面展开图、二元一次方程组和一元二次方程等核心知识，培养创新意识，提高运算能力、数据观念和几何直观等核心素养 综合能力目标 在拆解和分析包装纸盒的过程中，学会用数学的眼光观察包装纸盒的不同形状，感受不同设计方案的差异性，在将立体图形展开为平面图形的过程中，培养转化思想 在决策最优方案过程中，学会用数学的思维思考剪裁策略，用数学的方式反思生活实践，培养推理能力和运算能力，作出合理决策 在总结和撰写课题报告的过程中，学会用数学的语言表达剪裁方案的设计原理，从理论到实践再从实践到理论，培养几何直观和抽象能力等核心素养 精神品质目标 在项目化问题解决过程中，全面培养动手能力、交流能力和合作能力，通过渗透节能减排的德育和纸盒绘制的美育，落实育人价值 ]

3. 进阶维度

该项目通过追踪学生对立体图形表面展开图和相似三角形的发展水平，了解学生整体的学习进程，提升数学核心素养.

4. 进阶水平

（1）进阶阶段1：课前导学，任务前置.

情境1：众所周知，纸张的生产是以破坏环境为代价的. 资料显示，目前我国每生产1吨纸就要耗费约20棵大树、100立方米水. 如果每人每天浪费1张纸，全国每天就要浪费约2 700吨纸、54 000棵大树、270 000吨水.

任务1：收集和认识包装纸盒，记录相关资料.

任务2：拆解和分析包装纸盒，探究结构特征.

任务3：在5 × 5的方格纸中，探究棱长为1的密闭立方体包装纸盒的表面展开图有哪几种. 在预学单中画出各类不同的表面展开图.

学业表现：能够基于情境1，树立节能减排的环保意识；在任务1中，能够将实物立体图形抽象为数学中的理想几何体，并从数学的角度分析其结构特征，培养抽象能力；在任务2中，能够用数学的思维反思生活实物，培养几何直观和空间观念，寻找生活中的数学韵味；在任务3中，能够对平面几何图形的位置摆放进行构思，画出密闭立方体的展开图，培养空间观念.

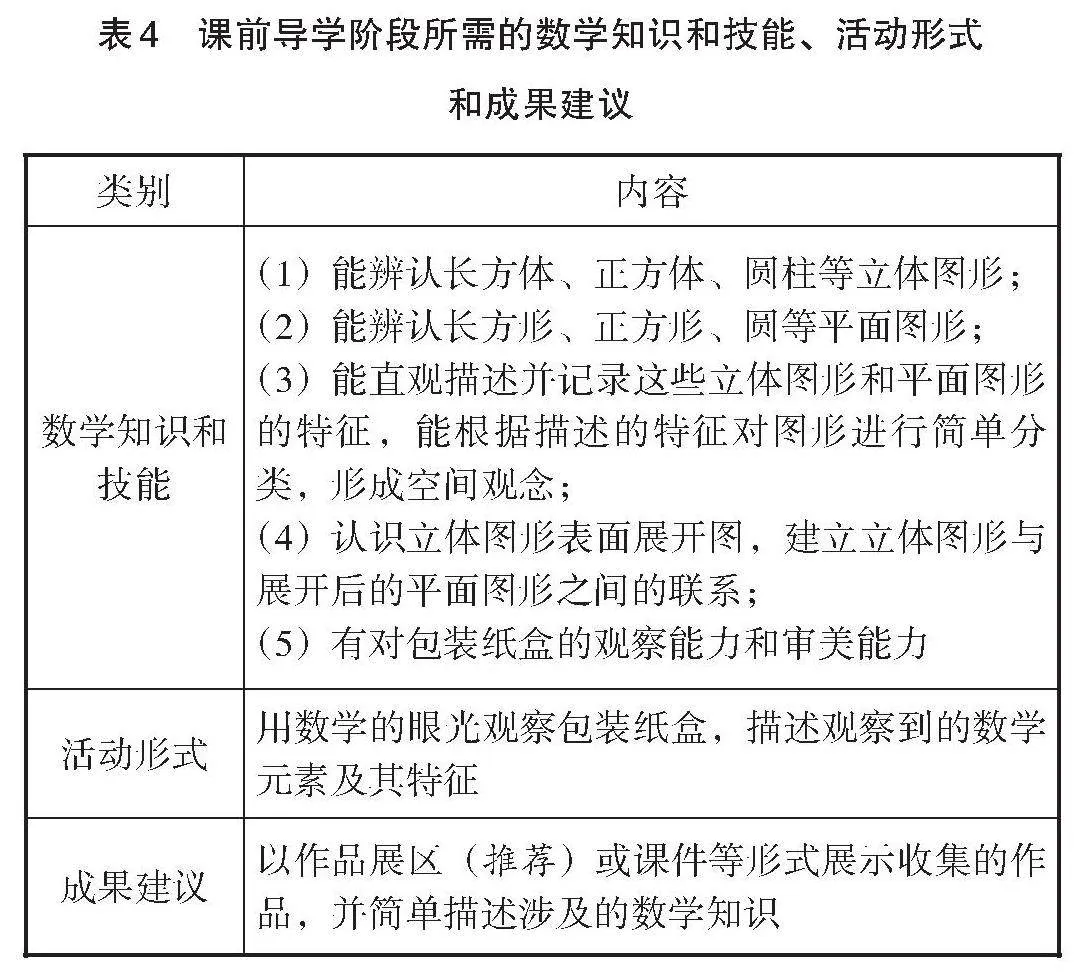
表4给出了课前导学阶段所需要的数学知识和技能、活动形式及成果建议.

表4 课前导学阶段所需的数学知识和技能、活动形式

和成果建议

[类别 内容 数学知识和技能 （1）能辨认长方体、正方体、圆柱等立体图形；

（2）能辨认长方形、正方形、圆等平面图形；

（3）能直观描述并记录这些立体图形和平面图形的特征，能根据描述的特征对图形进行简单分类，形成空间观念；

（4）认识立体图形表面展开图，建立立体图形与展开后的平面图形之间的联系；

（5）有对包装纸盒的观察能力和审美能力 活动形式 用数学的眼光观察包装纸盒，描述观察到的数学元素及其特征 成果建议 以作品展区（推荐）或课件等形式展示收集的作品，并简单描述涉及的数学知识 ]

【教学说明】勤俭节约是中华民族的传统美德. 利用情境1渗透德育，推进“大思政”建设. 任务1和任务2中的开放性问题设计，通过让学生用数学的眼光“看”包装纸盒，发现包装纸盒中的数学元素，使学生感受几何图形的对称之美、变换之美和组合之趣，实现“低起点、多层次”的个性化教学. 任务3可以唤醒学生对立体图形的表面展开图知识点的记忆，激发学生学习的主观能动性，减轻课中的学习压力.

（2）进阶阶段2：积累经验，初探项目.

小组合作展示：课中展示任务1、任务2和任务3的课前预学成果.

学业表现：用数学的眼光“看”包装纸盒，描述看到的数学元素及其特征，能够剖析寻找立体图形展开图的思考路径.

【教学说明】借助学具（正方形磁力片），鼓励学生动手操作、动脑想象，感知立体图形和平面图形之间的转化及这两类图形的关联. 通过小组的课前探究和师生、生生的课中合作，确定密闭立方体包装纸盒的表面展开图种类，为下一环节的画图设计和计算论证作铺垫.

（3）进阶阶段3：创设情境，呈现项目.

情境2：某公司推出一款环保包装盒，一个包装盒由一张卡纸折叠而成，其组装过程更加节省劳动力. 根据计算，一个纸盒的设计最高能降低40%的包装成本，还能避免过度包装带来的资源浪费.

任务4：用一张边长为20 cm的正方形纸片，探究如何剪裁出一张展开图，并将这张展开图折叠、制作成一个容积尽可能大的密闭立方体包装纸盒.（不计黏合处、不重叠.）

学业表现：在情境2和任务4中，能感受到在原材料有限的情况下，设计容积尽可能大的包装纸盒对节能减排的意义和价值.

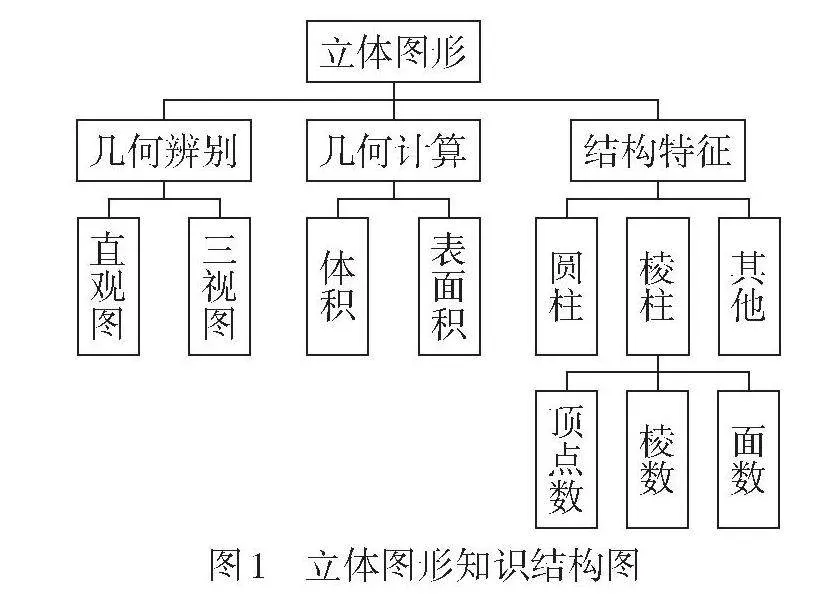
【教学说明】教师通过微视频展示情境2及学生手工制作密闭立方体包装纸盒的过程. 借助短视频的个e28320c3d0f36aa840c9c759fac8e174b2c1071bde4b508619c1a5cda122a562性化制作，既能起到示范性作用，又符合学生多样化的审美需求. 通过任务4，可以串联各学段的学科核心知识，特别是相似三角形和立体图形的知识，其知识结构如图1所示. 该知识结构图为数学项目学习的开展和问题的解决提供了丰富的素材.

[立体图形][几何辨别][直观图][三视图] [几何计算][体积][表面积] [结构特征][圆柱][棱柱] [其他][顶点数][棱数] [面数] [图1 立体图形知识结构图]

（4）进阶阶段4：设计方案，探究项目.

小组合作探究1：（拆解项目，特例设计，巧设基础性问题）在边长为20 cm的正方形纸片中，将表面展开图横向放置.

学业表现：能够借助学具拼图及计算发现容积尽可能大的正方体表面展开图设计方案.

如图2，当将表面展开图横向放置时，密闭立方体包装纸盒的棱长为4 cm或5 cm.

[（a）][（b）][（c）][（d）][（e）][图2 部分横向放置的作品设计

]

小组合作探究2：（推进项目，优化设计，巧设发展性问题）在边长为20 cm的正方形纸片中，将正方体表面展开图斜向放置.

学业表现：借助正方形磁力片，猜想容积尽可能大的裁剪方案并进行理论计算.

如图3，当将正方体表面展开图斜向放置时，密闭立方体包装纸盒的棱长分别为[1023 cm，] [4345 cm，][202619 cm]，[552 cm]，[42 cm].

[（e）] [（b）] [（d）] [（a）] [（c）][图3 部分斜向放置的作品设计

]

小组合作探究3：（深化项目，创新设计，巧解挑战性问题）探究容积更大的设计方案.

学业表现：借助等腰直角三角形、矩形和正方形磁力片，部分学生寻找到了容积更大的设计方案.

如图4，密闭立方体包装纸盒的棱长分别为4 cm，[52 cm]，[42 cm]，[407 cm].

[（a）] [（c）] [（b）] [（d）][图4 部分学生的创新作品设计

]

表5给出了课中研学阶段所需的数学知识和技能、活动形式和成果建议.

表5 课中研学阶段所需的数学知识和技能、活动形式

和成果建议

[类别 内容 数学知识和技能 （1）了解相似三角形的性质定理和判定定理；

（2）掌握等腰三角形和直角三角形的性质定理和判定定理；

（3）掌握二元一次方程组的解法；

（4）运用勾股定理解决问题；

（5）发展抽象能力、推理能力、运算能力、几何直观、模型观念、数据观念和创新意识 活动形式 用数学的眼光观察包装纸盒，借助学具进行猜想、验证、推理和择优 成果建议 从建模到解模，从猜想到验证，描述包装纸盒的设计全过程 ]

【教学说明】从横向放置展开图这一特例入手，呈现指向明确、计算简单的基础性问题，使得每名学生都能获得一定的数学知识，不同的学生在数学上得到不同的发展. 在探究1中的设计经验的基础上，利用探究2将学生的学习重心转移到计算上来. 通过分析正方形中直角折线段长度的求法，有利于培养学生的抽象能力和运算能力. 立足学生思维的最近发展区，考虑学生在探究1和探究2中已经达到的水平，通过探究3发展学生的高阶思维，培养学生的空间观念和创新意识.

（5）进阶阶段5：课后延学，学业测评.

任务5：（发展项目，迭代设计，巧探延学性问题）在一张长为36 cm、宽为24 cm的矩形纸片中，如何剪裁出一张正方体的表面展开图，并将这张展开图折叠制作成一个容积尽可能大的无盖立方体包装纸盒？（不计黏合处、不重叠.）

针对上述问题，各小组合作探究并汇报探究过程中遇到的困难及解决的办法，呈现小组的最优设计方案.

任务6：制作包装纸盒，并展示和介绍包装纸盒.

任务7：撰写课题报告，并进行小组汇报.

学业测评：针对该项目成果，采取三维立体定量评价和定性评价相结合的评价方式. 定量评价包括学生自评、小组互评和教师评价三个维度，涉及过程性评价和结果性评价两个部分. 项目成果立体评价如表6所示.

表6 项目成果立体评价表

[评价标准 优秀得4分，良好得3分，一般得2分，合格得1分 评价内容 评价分数 自评 互评 师评 项目过程评价 能综合运用数学知识和技能，积极主动地参与方案的设计及包装纸盒的制作 能正确表达自己的想法 尊重他人的建议并能进行有效沟通 具有创新能力和批判能力，遇到困难不退缩、不放弃 能利用各种资源解决问题 活动过程记录清晰、完整 项目结果评价 能根据问题寻求包装纸盒设计方案 包装纸盒有图案和文字的美术设计 汇报表达流畅、语言逻辑清晰 撰写课题研究报告 综合评定 ]

定性评价的内容如图5所示.

[在本次项目活动中，用文字进一步描述在该项目活动过程中，

你的困惑： ；

你的收获： ；

你的建议： ；

你运用到的数学知识和能力： ；

你的最优方案： ][图5]

学业表现：在任务5中，能够借助正方形磁力片猜想体积尽可能大的裁剪方案并进行计算验证.

如图6，无盖立方体包装纸盒的棱长分别为[9 cm]，[62 cm]，[45 cm]，[45 cm]，[3237 cm].

[（a）] [（b）] [（c）] [（d）] [（e）][图6 部分学生的作品设计

]

在任务6中，能够运用跨学科知识（美学知识、语言知识、劳动技术知识和广告学知识等）自制精美包装纸盒，将知识运用到现实情境中，培养几何直观和动手实践能力. 在任务7中，能够对项目化问题解决的全过程进行总结，提升对数学知识的研究意识和应用意识.

表7给出了课后延学阶段所需的数学知识和技能、活动形式和成果建议.

表7 课后延学阶段所需的数学知识和技能、活动形式

和成果建议

[类别 内容 数学知识和技能 （1）了解相似三角形的性质定理和判定定理；

（2）掌握等腰三角形和直角三角形的性质定理和判定定理；

（3）掌握二元一次方程组的解法；

（4）运用勾股定理解决问题；

（5）发展抽象能力、推理能力、运算能力、几何直观、模型观念、数据观念和创新意识 活动形式 用数学的思维设计和绘制包装纸盒，用数学的语言撰写课题报告 成果建议 展示设计的包装纸盒作品，并撰写设计说明，注明姓名和作品名称；制作课件，简明扼要地介绍包装纸盒设计和制作的全过程，并描述涉及的数学知识和方法 ]

【教学说明】类比课前情境和课中情境的学习过程，本环节对无盖立方体包装纸盒的设计和绘制方案进行再梳理、再巩固. 在决策最优方案的过程中，学会用数学的思维思考剪裁策略，用数学的方式反思生活实践，培养了学生的推理能力和运算能力. 在绘制包装纸盒实物模型的过程中，运用平面设计等知识技能，渗透纸盒绘制中的美育，培养了学生的创新意识. 在撰写课题报告的过程中，学会用数学的语言表达剪裁方案的设计原理，从理论到实践再从实践到理论，培养了学生的几何直观和抽象能力，使学生积累了基本思想、基本方法和基本活动经验.

四、项目反思

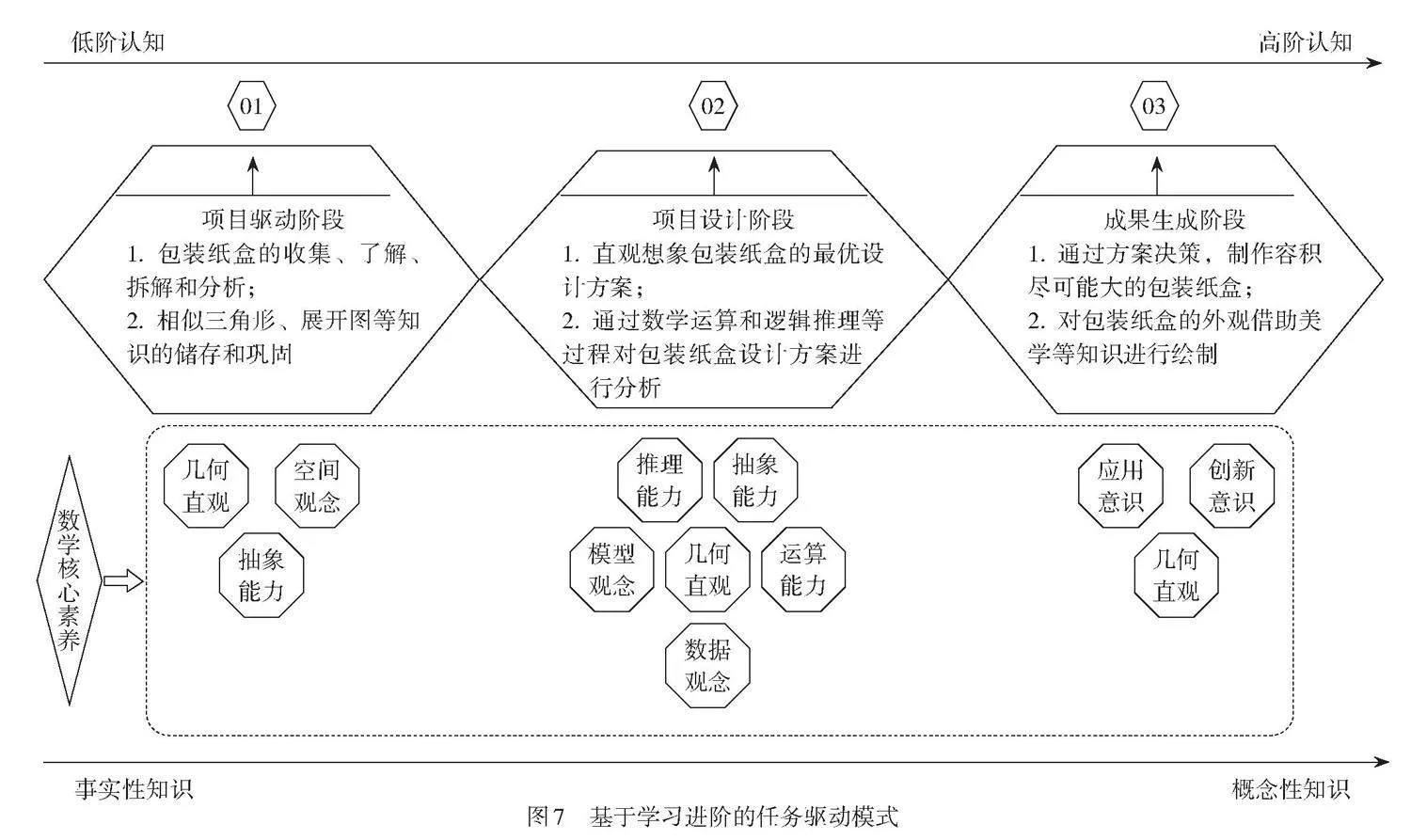
1. 关注进阶路径，培养高阶思维

在“包装纸盒的设计”项目中，学生经历了三个阶段的进阶路径（如图7），实现了从项目驱动、项目设计到成果生成的目的. 学生通过计算、探究、表征、合作、直观想象、动手操作和绘图设计等过程，经历观察包装纸盒、设计包装纸盒、优化方案设计、制作包装纸盒、撰写设计报告和交流展示成果等环节，最终完成包装纸盒产品制作. 本项目用事实性知识支撑概念性知识的形成，以实现从低阶认知到高阶认知的跨越.

2. 重视数学建模，提升核心素养

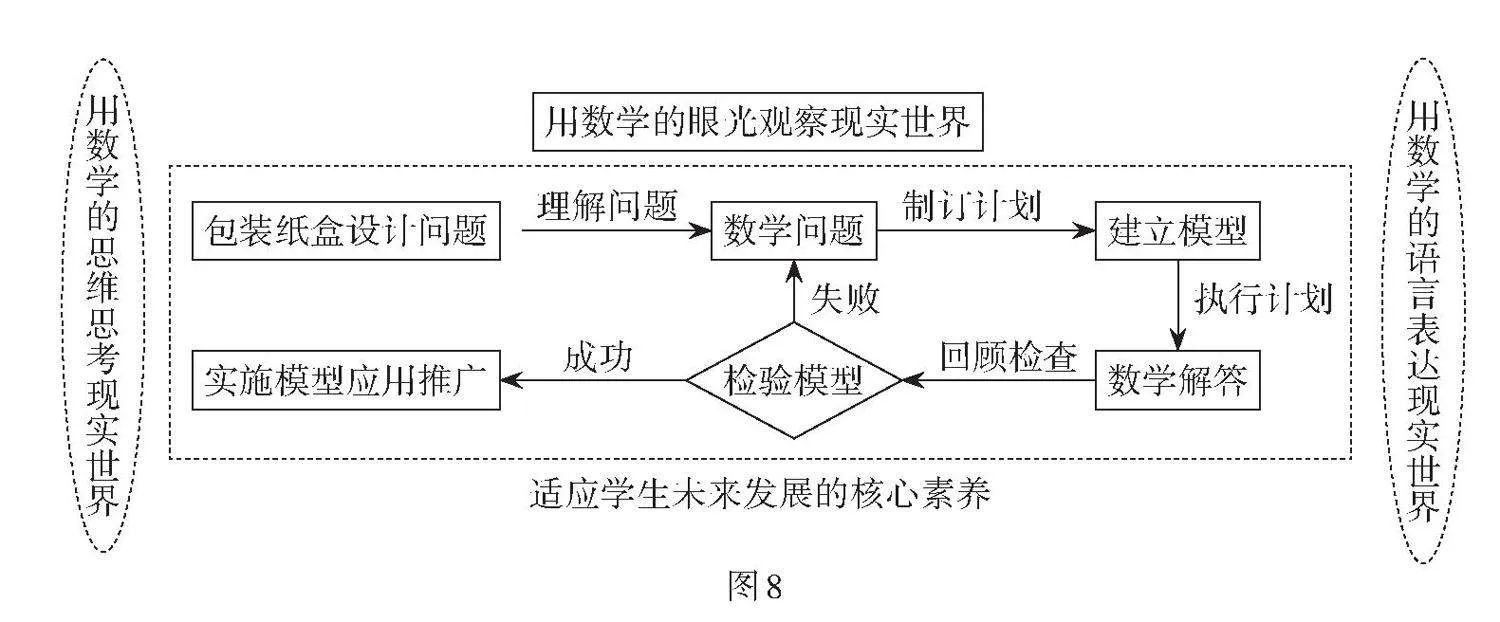
传统的数学教育往往是针对数学问题进行解决，而适应未来需求的教育应该是在真实的情境中去解决真实问题.《标准》指出，项目学习教学所涉及的问题主要是现实世界中具有开放性的问题，问题解决需要将现实问题转化为数学问题. 由此可见，“真情境”是衡量项目优劣的首要指标，而数学建模是联系数学与现实生活的基本途径. 该项目中，从现实问题中的情境1和情境2出发提出项目主题，设置开放性任务4和任务5. 在学生分组合作完成探究1、探究2和探究3后，教师及时引导学生进行提炼和总结，生成图8，同时借助图8完成任务5、任务6和任务7，得到包装纸盒裁剪问题的可视化解决策略.

3. 构建任务驱动，优化进阶模式

教学有法，贵在得法. 针对本项目形成了基于任务驱动的“三场四环”递进式学习模式（如图9），即以课前场景、课中场景、课后场景为三个主要板块，以任务驱动、任务挑战、任务迭代、任务进阶为四个基本环节. 考虑到项目式学习需要具备小组合作探究和设置开放性问题等特点，本项目力求做足课前场景，做实课中场景，做优课后场景. 在课前场景中，教师下发预学单，分析学生的进阶起点，明确学生的进阶终点. 在课中场景中，通过导学单的引领，明确学生的进阶水平，全程追踪进阶维度，分析学生的学业表现. 在课后场景中，通过延学单的设计，助力学生生成研究成果，助力教师开展学业测评.

作者简介：许笑笑（1992— ），女，中学一级教师，主要从事数学教学研究；

黄信永（1989— ），男，中学一级教师，主要从事初中数学课堂教学研究.