基于数学理解性学习的教学实践与思考

摘 要：以“有理数与无理数”一课的教学实践为例，提出数学理解性学习的形成策略.

关键词：有理数与无理数；理解性学习；数学活动经验

中图分类号：G633.6 文献标识码：A 文章编号：1673-8284（2024）10-0031-05

引用格式：黄贤明. 基于数学理解性学习的教学实践与思考：以“有理数与无理数”一课为例［J］. 中国数学教育（初中版），2024（10）：31-35.

基金项目：2022年度江苏省教育科学规划课题——大概念观照下初中数学前建构教学的实践研究（C/2022/02/01）.

作者简介：黄贤明（1999— ），男，中学二级教师，主要从事初中数学教学研究.

数学学习重在理解. 有理数与无理数的概念是学生进入初中阶段后学习的第一个概念，它们是因数学知识结构内部发展的需要而生成的数学概念. 在探索有理数时，学生提取、归纳整数与分数的共同属性；而对无理数的探索过程是学生发现、感受和思考无限不循环小数的过程.《义务教育数学课程标准（2022年版）》（以下简称《标准》）对有理数和无理数的要求为：理解有理数的意义，了解无理数. 由此可见，《标准》对有理数的要求是在掌握有理数概念的基础上理解其意义. 本文以苏科版《义务教育教科书·数学》七年级上册“2.2 有理数与无理数”一课的教学为例，基于数学理解性学习进行教学实践与思考.

一、基于数学理解的内涵阐述

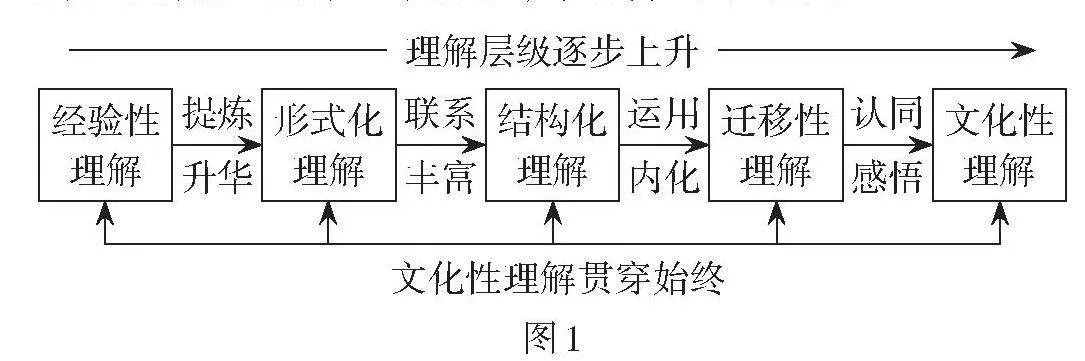
数学理解是指个体建立了包含数学概念、法则等内容的内部知识网络. 数学理解不是一蹴而就的，而是一个层级发展的过程，是不断丰富、完善认知结构和知识意义的过程. 数学理解性学习层级发展的过程模型主要阐述了学生数学理解性学习的发展会依次经历经验性理解、形式化理解、结构化理解、迁移性理解和文化性理解五个阶段，具体如图1所示.

经验性理解是指学习者从原有认知结构中提取出对新知识的起始性理解，但这种理解往往掺杂着个性化理解，是模糊的、不全面的. 教师在教学中应该积极把握学生已有的经验，寻找新旧内容之间的联结点，让学生利用已有经验促进对新知的理解. 形式化理解是指通过接受有效的刺激进行整理、组织、概括和重新表述等数学活动，使经验性知识逐渐摆脱数学内容的非本质属性，进而获得对其本质属性的深刻理解. 结构化理解实际上是一种结构关联性理解，强调在一种知识的关系脉络中把握相关知识的内涵与本质. 迁移性理解是指个体在结构化理解的基础上，能够灵活运用知识解决问题，将所学知识迁移到陌生的情境中，运用到问题的解决中. 文化性理解贯穿数学理解的始终，是数学理解的深层次指向. 教师在教学中应该有意识地推进文化性理解，增强学生的认同感，鼓励学生深入了解数学内容背后的文化历史，形成对数学文化的个人感悟，进而丰富经验性理解，加深形式化理解，拓展结构化理解，完善迁移性理解.

二、对学生理解有理数与无理数过程中的障碍分析

1. 已有经验引发认知冲突

有理数概念的获得是对整数与分数共同本质属性的提取，即都可以化为分数形式. 学生基于已有认知，能够知道整数与分数的区别、有限小数与分数的关系、整数与分数形式的异同，但是随着将整数以分数形式表示出来，这就与学生已有的认知经验（分数的分母不为1）矛盾，导致学生产生了认知冲突，使得学生对有理数概念的理解不透彻.

2. 缺乏记忆导致概念混淆

布卢姆教育目标分类法将认知领域分为记忆、理解、运用、分析、评价和创造六个部分，其中理解是在知道的基础上发生的. 如果学生不记忆概念或片面记忆概念，随着对不同概念的不断学习与积累，就会导致概念记忆的混淆. 以对[-27]的分类为例，部分学生将其归类为无理数，原因是经过运算发现[-27]≈[-0.285 71…]，以为这个小数好像是无限不循环小数，认定[-27]为无理数. 这显然是错误的. 原因之一，[-27=-0.2·85 714·]，是一个无限循环小数；原因之二，[-27]是两个整数之比的形式，满足有理数的定义. 究其原因，学生对于有理数和无理数的概念掌握不牢固，只关注所给数的小数形式.

3. 自身能力影响体系构建

有些学生在分类有理数、利用逼近思想感受无理数、概念辨析等环节频频出错，导致其对概念的学习停留在记忆的层级，对于概念的运用浮于机械地模仿. 这终将导致学生无法独立构建有理数和无理数的概念体系，也就无法达到对概念的深入理解的层次.

三、基于数学理解性学习的“有理数与无理数”的教学过程设计

1. 复习思考：激活经验性理解

问题1：读一读，并比较下列两组数，它们有什么区别？

（1）+7，998，-1 035，0；

（2）[12]，[-312]，[23]，[-14].

问题2：观察这两组数，它们还能再细分吗？

教师引导学生利用大括号将整数和分数分类，具体分类情况如下.

[整数正整数：+7，9980负整数：-1 035]

[分数正分数： 12， 23负分数：-312，-14]

问题3：观察上述分数，思考什么是分数，什么是分数形式.

【设计意图】通过对具体数的分类与思考，引导学生回顾整数与分数的概念及其分类，并利用具体分数指出分数的形式，激活学生已有的经验，为有理数概念的本质属性的提取作铺垫.

2. 归纳提取：生成形式化理解

活动1：尝试将0.1，-0.25，4，-3，0化为分数形式.

依托原有的经验，学生能很快地将0.1化为[110]，将-0.25化为[-14]. 但对于整数而言，则需要教师进一步辅助辨析分数与分数形式的区别，引导学生将整数表示为分母是1的分数.

问题4：0.1，-0.25等都是有限小数，可以化为分数形式. 那么0.333 3…，0.666 6…等无限循环小数能化为分数形式吗？

小结：经过探究发现，分数（有限小数、无限循环小数）和整数都可以统一为分数形式，我们将能够写成分数形式[mn]（m，n是整数，n ≠ 0）的数叫作有理数.

教师完善板书，如图2所示.

活动2：结合已有经验，尝试采用不同的方式对有理数进行分类.

学生进行小组交流，教师补充完善，得到的结果如下.

[有理数整数正整数0负整数分数正分数负分数] [有理数正有理数正整数正分数0负有理数负整数负分数]

问题5：无限小数还包括无限不循环小数，你能举几个无限不循环小数的例子吗？无限不循环小数能化为分数形式吗？

【设计意图】通过活动1，将学生已有的经验进行组织、再现，围绕将有限小数进行分数形式的转化，完善学生的经验性理解，打破学生的思维困境，使之自然理解整数的分数化过程，再加以无限循环小数的补充，直观呈现整数与分数之间的共性，使得经验性知识逐步服务于有理数概念本质属性的提取，形成深层次的认识，进而在活动2的探究中获得对有理数概念及其分类的形式化理解.

活动3：尝试利用面积是4的正方形ABCD（如图3）画出一个面积是2的正方形EFGH.

[A][B][C][D][图3]

提示：尝试利用正方形纸片动手操作，探索发现分别连接正方形ABCD四边的中点得到的正方形EFGH（如图4）面积为2.

[图4] [2][A][B][C][D][E][F][G][H]

问题6：若设正方形EFGH的边长为a，且[a2=][2]，则边长a是有理数吗？

活动4：探究面积为2的正方形的边长a的值.

教师引导学生观察图4，启发学生思考：面积为2的正方形的大小介于面积为4和面积为1的正方形之间，故其边长a的大小也应该介于1到2之间. 而后借助Excel表格，依次给出正方形的边长与面积的数据（如图5），让学生逐步缩小a的范围.

问题7：还可以继续确定边长a的取值范围吗？a是有限小数吗？

师：借助计算器求得a = 1.414 213 562 373…，它是一个无限不循环小数，我们将无限不循环小数叫作无理数. 仿照有理数的分类，无理数可以分为正无理数和负无理数.

活动5：尝试说出一些无理数.

① 围绕π产生的数；② 依托正方形的面积等，给出不可以开方的数；③ 构造如3.020 220 222…等形式的无理数.

【设计意图】通过活动3的动手尝试，得到面积为2的正方形，让学生在实践操作中积累数学活动经验.而后借助具体图形对边长a的大小进行探索，揭示已有的数无法表示边长，并通过活动4的探究活动，让学生发现边长a不具备有理数的特征，属于无限不循环小数，自然生成无理数的概念，感受逼近、合情推理等数学思想方法在数学探究过程中的价值. 最后以活动5来丰富相关无理数的实例，促进学生形式化理解的形成.

3. 历史再现：渗透文化性理解

问题8：有理数的“理”是什么含义？

古希腊毕达哥拉斯学派提出“万物皆数”理论，这里的“数”指的是有理数，即一切数都可以表示成整数或整数之比. 有理数也应该称为“可比数”或“成比例的数”. 1607年，明代数学家徐光启将有理数“proportion”翻译为古汉语的“理”，“理”就是“比值”的意思.

【设计意图】有理数名称的由来源远流长，是人类智慧的结晶. 就定义来说，有理数更应该称为“可比数”，但由于古汉语的翻译问题及各国之间的文化差异，最终形成了“有理数”的名称. 以有理数的发展历史开阔学生的视野，揭示有理数中“理”的内涵，促进学生初步形成对有理数概念的文化性理解.

4. 概念辨析：引导结构化理解

练习1：判断下列说法是否正确，并说明理由.

（1）有理数都是有限小数；

（2）有理数包括正数、负数和0；

（3）有理数包括整数和分数；

（4）无限小数都是无理数；

（5）无理数都是无限小数.

练习2：将下列各数填在相应的集合内：-6，9.3，-[27]，42，0，0.333…，1.414 114 111，[π2]，3.303 003 000 3…，

-3.141 592 6.

正数集合：｛ …｝；

负数集合：｛ …｝；

有理数集合：｛ …｝；

无理数集合：｛ …｝.

问题9：-[27]经过计算是-0.285 71…，看似无限不循环小数，为什么它却是有理数？为什么[π2]有分数线，但它不是分数、有理数？如何判断一个数是有理数还是无理数？有理数和无理数的本质区别在哪里？

【设计意图】经过形式化理解，学生对于有理数和无理数的概念已经有了一定的认识. 通过概念辨析及数的分类的练习，进行精细的信息加工，纠正学生对概念的错误认识，将有理数和无理数的概念与已有认知结构结合起来，类比学生已有的知识经验，促进学生对新概念的记忆与存储，使得学生从单一的形式化理解发展到具有关联性的结构化理解.

5. 拓展思考：指向迁移性理解

练习3：回答下列问题.

（1）如图6，A，B所表示的集合代表什么含义？有哪些数无法在图中表示出来？

[整数集合][正数集合][无理数集合][A][B][图6][…][…][…]

（2）写出4个数，同时满足以下3个条件：① 其中3个数属于有理数集合；② 其中2个数属于负数集合；③ 其中2个数属于整数集合.

（3）将（2）中的4个数和-12，3.515 115 111…，0.666…，-2π填入图中的集合.

练习4：设面积为3π的圆的半径为x，x是有理数吗？试说明理由，并估计x的整数部分是多少. 同理，面积为5π，10π的圆，你能估计出它们半径的整数部分吗？

【设计意图】这两道练习题的设计旨在考查学生对有理数和无理数概念的理解及迁移应用能力. 在练习3的设计中，设问从封闭到开放再回归到封闭，使学生在设计、评价、分类的过程中，提升“四能”，进一步加深对概念的理解. 在练习4的设计中，学生再次感受无理数的存在，进一步应用逼近思想解决问题.

6. 自我总结：促进文化性理解

教师引导学生总结本节课所学内容，并形成知识建构.

（1）通过本节课的学习，你对有理数和无理数有了哪些认识？它们与我们所学的正数和负数存在哪些联系与区别？

（2）本节课的学习中蕴含着哪些数学思想方法？

（3）课后拓展：查阅相关有理数与无理数的历史故事.

【设计意图】通过自我总结，引导学生回顾课堂所学的概念并系统梳理知识体系. 同时，教师应该关注学生个体的知识构建情况，以谈感想与疑惑等方式，让学生在“说”的过程中进一步理解、内化概念，形成对知识综合性、整体性的认识.

四、教学反思

在常态化教学中，教师应该关注学生对知识的应用情况（即结构化理解和迁移性理解环节）. 基于数学理解性学习视角，经验性理解、形式化理解与文化性理解这三大环节也是在学生理解知识的过程中必不可少的.

1. 以旧启新，依托经验性理解

建构主义理论认为，数学知识不可能以实体的形式存在于个体之外. 对初中阶段的学生而言，他们已经有了小学阶段的数学知识基础，拥有了一定的生活和学习经验，并且这些经验是在不断积累、更新与完善的. 在初中数学教学中，教师要基于学生已有的经验，重视对学生经验的激活，让学生的已有经验服务于新知的获得与理解，实现概念的自主构建和自然生长. 因此，在“有理数与无理数”一课的教学中，教师从对数的分类的探究出发，激活学生对于分数形式的认识，促进学生对整数与分数本质属性的提取.

2. 直观呈现，重视形式化理解

形式化理解是数学理解性学习的关键一环，既是学习概念的核心，也是后续结构化理解、迁移性理解的重要基础. 学生经过对经验的激活、提取，为新知的获得搭好了“脚手架”. 在“有理数与无理数”一课中，学生依托经验获得了分数形式. 下一步就需要巧妙地利用多种方式（如提问、动手操作、列表等）直观呈现概念的本质属性，引导学生自然构建概念，获得概念的内涵，促使学生形成对概念的形式化理解.

3. 巧妙渗透，促进文化性理解

文化是数学课堂的“润滑剂”，对学生个人成长和素养发展具有重要作用. 文化性理解渗透于数学理解性学习的各个环节，不受学生认知基础的限制. 在“有理数与无理数”一课的教学中，文化性理解的内容主要涉及以下两点. 其一，有理数与无理数都蕴藏着丰富的历史文化底蕴，如有理数名称的由来、无理数的发现，等等. 但教学设计中只呈现了有理数名称的由来，目的在于用数学史促进学生对有理数概念的理解，让“理”与“比例”之间建立起文化性桥梁，既拓宽了学生的视野，也深化了学生对概念的理解. 其二，在对有理数与无理数概念的探索中体现了多种数学思想方法，如抽象思想、逼近思想、归纳猜想、类比、分类等. 这些数学思想方法存在于学生的自我总结中，为学生今后的数学探究活动累积了重要的探究经验.

参考文献：

［1］周正峰，任宏章. 关于初中数学概念生成性教学的思考：以“有理数与无理数”的教学为例［J］. 中学数学月刊，2019（10）：39-40.

［2］中华人民共和国教育部. 义务教育数学课程标准（2022年版）［M］. 北京：北京师范大学出版社，2022.

［3］吕林海. 数学理解性学习与教学：文化的视角［M］. 北京：教育科学出版社，2013.

［4］常经营，兰伟彬. 布鲁姆教育目标分类的新发展［J］. 南阳师范学院学报，2008（5）：84-86.

［5］曾峥，杨豫晖，李学良. 数学史融入初中课堂的案例研究［J］. 数学教育学报，2019，28（1）：12-18.

［6］张涛，代钦，李春兰. 数学教学视域下理解与应用皮亚杰建构主义理论［J］. 数学教育学报，2024，33（3）：96-102.