基于学生思考路径的习题解法研究与反思一例

摘 要：针对一道填空题的解法，两名学生分别基于“几何模型”和“函数最值模型”的视角，提供了与预设解题思路完全不同的思考路径. 通过对这两种思考路径的进一步研究，发现了几种意料之外的解法. 同时，基于学生思考路径的解法研究，提出几点思考.

关键词：思考路径；解法探究；解后反思

中图分类号：G633.6 文献标识码：A 文章编号：1673-8284（2024）10-0061-04

引用格式：范明明，郑金. 基于学生思考路径的习题解法研究与反思一例［J］. 中国数学教育（初中版），2024（10）：61-64.

基金项目：广东省2022年度中小学数学教学研究专项课题——指向核心素养的初中数学习题课教学策略研究（GDJY-2022-M-b71）.

作者简介：范明明（1988— ），男，中学一级教师，主要从事初中数学教育教学研究；

郑金（1989— ），女，中学一级教师，主要从事初中数学教育教学研究.

在九年级备考复习阶段的一次巩固练习中，有一道填空题难度较大，学生的完成情况不理想. 在笔者讲解题目的解题思路后，学生虽然恍然大悟但也表示很难想到. 在笔者提出“大家是如何思考该问题的？”这一追问后，学生纷纷给出了自己的思考路径. 当笔者根据学生的思考路径继续研究题目时，发现了意想不到的解法. 现整理成文，与同行分享.

题目 如图1，在正方形[ABCD]中，[AB=2 cm]，点 E为 边BC 中点，M ，N 分别是边 CD ， AB 上的动点，连接 MN ，AE，且始终保持[MN⊥AE]，连接AM，EN，则[AM+EN]的最小值为__________.

一、预设的解题思路

该题是一道以正方形为背景的双动点求最值问题. 一般来说，求两条线段和的最小值问题的最终落脚点是“三点共线”，故线段 AM 和线段 EN 在线段 MN 的两侧是该问题求解的难点所在. 要想利用“三点共线”，就需要把 线段AM 和线段 EN 通过某种方式“移”到一起. 于是，想到将线段 AM 沿着 AE 的方向平移到 线段EF 处，如图 2 所示. 当 F ，E ，N 三点共线时，[EF+NE]的值最小，即[AM+][EN]的最小值为线段 NF 的长度.

随后，笔者根据[MN⊥AE]这一条件想到直角和直角三角形，进而想到勾股定理，继而思考是否可以以 NF 为一边构造直角三角形. 考虑到线段 EF 与线段 AM 平行且相等，于是自然地联想到连接 MF 构造平行四边形 AMFE . 由此，不仅可以推出[∠FMN=90°]，得到“[△FMN]是直角三角形”这一关键条件，还可以由平行四边形的性质得到[MF=AE=12+22=5]. 此时，求线段 MN 的长成为解决问题的关键 . 如图2，过点M作[MG⊥AB]于点G，易 证[△ABE≌][△MGN]. 所以[MN=5]. 在[Rt△FMN]中，由勾股定理，得[NF=MF2+MN2=][10]. 故[AM+][EN]的最小值为[10 cm].

当然，也可以将EN沿着EA的方向平移到AF处，如图3所示. 在[Rt△MNF]中亦可求出[MF=10]，即[AM+][EN]的最小值为[10 cm]，此处不再赘述.

二、学生的思考路径

在笔者向学生展示上述解题思路后，他们恍然大悟，在惊讶解法竟如此简单的同时，也有部分学生发出没想到或根本想不到的感叹. 当笔者提出“大家是如何思考该问题的？”的追问后，学生纷纷给出了自己的思考路径. 其中，有两名学生的思考路径比较典型，具体如下.

生1：题目所求的是[AM+EN]的最小值，从形式上看，容易想到“将军饮马”模型，利用该模型的一般思路是“对称 + 共线”，于是想到作点 M 关于线段 AB 的对称点 F . 如图4，连接 AF 和 NF ，则[AM=AF]. 但受方向和角度的影响，AF 和 EN 不能共线. 于是考虑将 AF 向 FN 转化. 但 由于点M 是动点，故 AF 和 NF 之间不存在明显的数量关系，解题陷入了困境. 我又换了一个角度作点 E 关于 AB 的对称点，但结果还是一样.

生2：由两条线段和的最小值问题联想到函数最值问题，即先用代数式表示线段的和，再结合自变量的取值范围和函数的增减性求其最小值. 如图5，过点 M 作[MF⊥AB]于点 F. 由[△ABE≌][△MFN]，得[FN=][BE=1.] 设[AF=x]，则[BN=1-x]. 设[AM+EN=y]，则[y=x2+22+][1-x2+12]，其中x的取值范围为[0≤x≤1]. 但是该函数的表达式中含有根号，无法求出y的最小值.

以上两名学生分别从几何和代数的角度思考了该问题. 虽然受已有经验的影响，两名学生没有求得最终结果，但是他们分析问题的思考路径无疑是值得称赞的，这也是比较符合大多数学生认知水平的思考方式.

三、基于学生思考路径的解法探究

虽然这两名学生没有求得最终结果，但是笔者认为这两种思路还有进一步研究的价值. 因此，笔者在课后对这两种思考路径作了更进一步地探究.

1. 从“将军饮马”到“将军遛马”

笔者在分析生1的思路后，发现AF 与 NE 之所以无法共线，原因在于线段 AF 的位置“不合适”，不符合运用“将军饮马”模型的基本条件. 笔者尝试转化线段 AM ，从而改变 AF 的位置，以满足“将军饮马”模型的运用条件. 结合图5，笔者想到可以连接DF（如图6），则[DF=AM]. 所以[AM+EN]的最小值等于[DF+][EN]的最小值. 此时，虽然还构不成“将军饮马”模型，但竟然得到了“将军饮马”模型的一个变式——“将军遛马”模型.

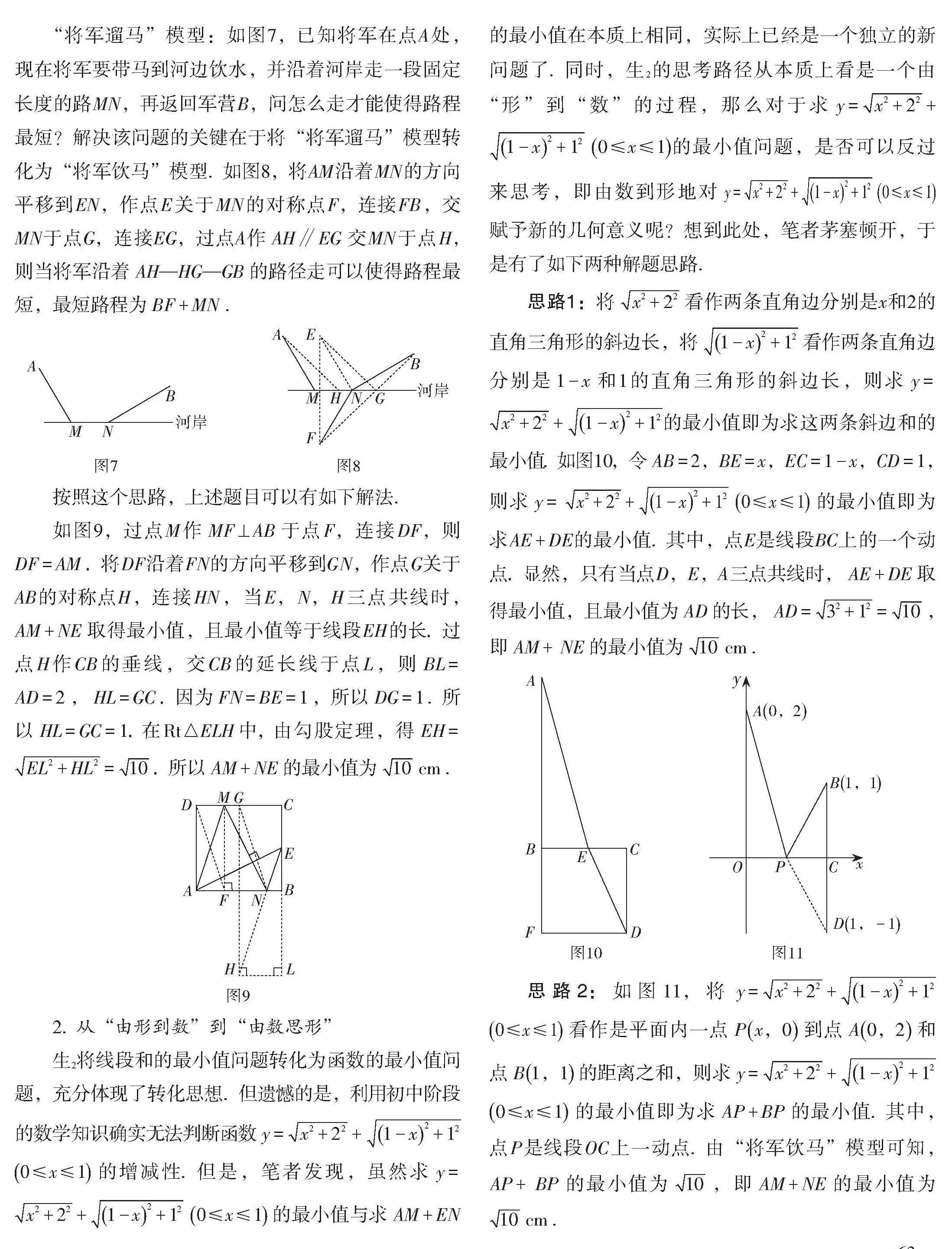
“将军遛马”模型：如图7，已知将军在点A 处，现在将军要带马到河边饮水，并沿着河岸走一段固定长度的路 MN，再返回军营 B，问怎么走才能使得路程最短？解决该问题的关键在于将“将军遛马”模型转化为“将军饮马”模型. 如图8，将 AM 沿着 MN 的方向平移到 EN，作点 E 关于 MN 的对称点 F，连接 FB ，交 MN 于点G，连接EG，过点A作[AH∥EG]交 MN 于点 H，则当将军沿着[AH—HG—GB]的路径走可以使得路程最短，最短路程为[BF+MN].

按照这个思路，上述题目可以有如下解法.

如图9，过点 M 作[MF⊥AB]于点 F，连接 DF，则[DF=AM]. 将 DF 沿着FN的方向平移到 G N，作点 G 关于 AB 的对称点 H ，连接 HN ，当 E， N，H 三点 共线时，[AM+NE]取得最小值，且最小值等于线段 EH 的长. 过点 H 作 CB 的垂线，交 CB 的延长线于点 L ，则[BL=][AD=2]，[HL=GC]. 因为[FN=BE=1]，所以[DG=1]. 所以[HL=GC=][1]. 在[Rt△ELH]中，由勾股定理，得[EH=][EL2+HL2=10]. 所以[AM+NE]的最小值为[10 cm].

2. 从“由形到数”到“由数思形”

生2将线段和的最小值问题转化为函数的最小值问题，充分体现了转化思想. 但遗憾的是，利用初中阶段的数学知识确实无法判断函数[y=x2+22+1-x2+12][0≤x≤1]的HgqmXr1QTqvx2YiLytKnHNiFSEEh05JFZsoN3vBstVo=增减性. 但是，笔者发现，虽然求[y=][x2+22+1-x2+12 0≤x≤1]的最小值与求[AM+EN]的最小值在本质上相同，实际上已经是一个独立的新问题了. 同时，生2的思考路径从本质上看是一个由“形”到“数”的过程，那么对于求[y=x2+22+][1-x2+12 0≤x≤1]的最小值问题，是否可以反过来思考，即由数到形地对[y=x2+22+1-x2+12 0≤x≤1]赋予新的几何意义呢？想到此处，笔者茅塞顿开，于是有了如下两种解题思路.

思路1：将[x2+22]看作两条直角边分别是x和2的直角三角形的斜边长，将[1-x2+12]看作两条直角边分别是[1-x]和1的直角三角形的斜边长，则求[y=][x2+22+][1-x2+12]的最小值即为求这两条斜边和的最小值. 如图10，令[AB=2，BE=x，EC=1-x，CD=1，] 则求[y=][x2+22+1-x2+12 0≤x≤1 ]的最小值即为求[AE+DE]的最小值. 其中，点E是线段BC上的一个动点. 显然，只有当点 D，E，A 三点共线时，[AE+DE]取得最小值，且最小值为[AD]的长，[AD=32+12=10]，即[AM+][NE]的最小值为[10 cm].

思路2：如图11，将[y=x2+22+1-x2+12][0≤x≤1 ]看作是平面内一点[Px，0]到点[A0，2]和点[B1，1]的距离之和，则求[y=x2+22+1-x2+12][0≤x≤1 ]的最小值即为求[AP+BP]的最小值. 其中，点 P 是线段 OC 上一动点. 由“将军饮马”模型可知，[AP+][BP]的最小值为[10]，即[AM+NE]的最小值为[10 cm].

四、解后反思

1. 广泛联想找思路，大胆尝试寻方向

解数学题，就其本质而论，就是寻求命题的条件与结论之间的逻辑联系. 整个解题的思维推理过程，实质上就是一系列的广泛联想过程. 联想的内容主要有相似问题的处理方法，类似条件的处理策略，可能相关的定理、方法或数学模型等. 换而言之，就是联想已往的解题经验和相关的数学模型. 例如，在预设的解题思路中，由两条线段和的最小值问题想到“三点共线”，进而想到将两条线段“移”到一起，正是受

以往解题经验的影响. 学生由[AM+NE]想到“将军饮马”模型和“函数最值”模型，也是联想相关数学模型的具体体现. 但是联想只能寻找可能的解题思路，在此基础上还需要配合大胆尝试才能验证解题方向的正确性，进而确定是否需要调整解题策略. 笔者基于生1的思考路径继续探究，正是将线段 AM 转化为线段 DF 并作出大胆尝试，才发现了“将军遛马”模型. 此外，从“由形到数”到“由数思形”的转变也是广泛联想和大胆尝试的具体体现. 当然，广泛联想和大胆尝试是在全面、深入加工题目信息基础上进行的解题活动，而不是思维定式般的机械模仿和套用.

2. 模型结构要理解，模型思想更关键

生1能从[AM+NE]的最小值联想到“将军饮马”模型，说明其对“将军饮马”模型的结构具有一定了解. 但是从生1作点 M 关于 AB 的对称点 F 的解题步骤来看，这种了解只停留在对该模型简单套用的层次，而没有深刻理解模型的本质和内涵. 由前文的解析过程可知，要想改变线段 AF 的位置，只能从“源头”上对线段 AM 进行转化，这显然已经超出了单纯记忆与复制模型结构的层次，是需要学生对“将军饮马”模型有深刻理解才能实现的模型建构，是模型思想的体现. 但是模型结构和模型思想之间存在本质的差异. 掌握模型结构只是对模型固有形态的一种静态理解，而模型思想则是通过分析、联想、建立（或选择）恰当的模型，并运用该模型的性质分析问题，使问题得以解决的思维策略，是一种动态的建构过程. 显然，掌握模型结构并不等于具有模型思想. 换句话说，生1解题思路受阻的根本原因在于其头脑中虽有模型结构但缺乏模型思想，因此在解题过程中只能对“将军饮马”模型进行简单的记忆与模仿，而不能自主地选择和建构.

3. 数形结合百般好，数形分离莫忽略

我们知道，数形结合是一种重要的数学方法，主要是指数与形之间的一一对应关系. 根据前后对应顺序的不同，这种对应关系应包含两个方面：一是从“数”到“形”的转化，二是从“形”到“数”的转化. 生2将求[AM+NE]的最小值转化为求[y=x2+22+][1-x2+12 0≤x≤1]的最小值，正是体现了由形到数的转化. 但“转化”这个词本就暗含了数与形的独立性，即数形结合的前提是数形分离. 事实上，在生2将[AM+NE]转化为[x2+22+][1-x2+12]后，“数”与“形”就已经实现了分离，求[y=x2+22+1-x2+12 ][0≤x≤1 ]的最小值已经成为了一个独立的新问题. 笔者正是在“数形分离”的基础上赋予了[x2+22+][1-x2+12 0≤x≤1]新的几何意义，从而继续了由“数”到“形”的转化，并最终求出结果. 事实上，只关注“数形结合”而忽略“数形分离”，正是导致生2解题思路受阻的根本原因. 综合分析此种解法，正是从“数形结合”到“数形分离”再到“数形结合”的探究过程.

参考文献：

［1］奚后知. 运用广泛联想法解数学题［J］. 数学通报，1986（5）：4-6.

［2］陈晶. 数学模型相关概念的厘清与教学思考［J］. 中学数学教学参考（下旬），2018（9）：63-64.

［3］吴有昌，郑锦松. 数形结合思想［J］. 中学数学教学参考（中旬），2018（1 / 2）：112-115.

［4］孙四周.“数形结合”与“数形分离”［J］. 中学数学教学参考（中旬），2021（12）：1.