对角互补模型探究

摘要：本文中以2024年江苏中招数学真题中的对角互补模型问题为例，深入探讨对角互补模型相关问题，旨在为学生提供一种有效的解题路径和策略，帮助学生提高解决此类问题的能力.

关键词：对角互补模型；解题策略；初中数学

对角互补模型是初中数学几何部分的重要内容之一，它基于角的互补性质，通过构造辅助线、利用相似三角形和全等三角形等方法来解决与补角相关的角度计算和证明问题.这类题目不仅考查学生对角的互补性质的理解，还考查学生的空间想象能力和逻辑推理能力.

1 真题

真题1（2024年江苏盐城中考数学第16题）如图1，在△ABC中，∠ACB=90°，AC=BC=22，点D是AC的中点，连接BD，将△BCD绕点B旋转，得到△BEF.连接CF，当CF∥AB时，CF=______.

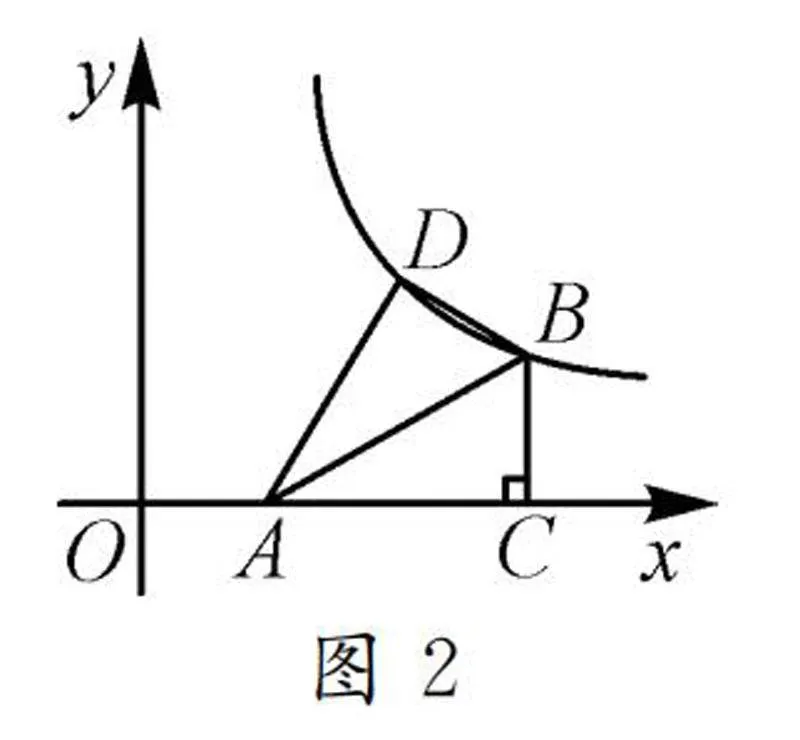
真题2（2024年江苏扬州中考数学第17题）如图2，在平面直角坐标系中，点A的坐标为（1，0），点B在反比例函数y=k/x（x＞0）的图象上，BC⊥x轴于点C，∠BAC=30°，将△ABC沿AB翻折，若点C的对应点D落在该反比例函数的图象上，则k的值为______.

2 对角互补模型的概念、性质及解题策略

对角互补模型特指四边形内存在一组对角角度之和为180°，同时满足至少一组邻边长度相等的特定几何形态.此类模型依据角度的特性，主要细分为含有90°和120°角的两种类型.在解决这类问题时，我们通常会采用两种主要的辅助线构造方法：一种是通过顶点作双重垂直线来形成全等的三角形，另一种则是通过图形的旋转操作来构建全等的三角形.这两种方法都能有效地帮助我们理解和解答涉及对角互补模型的问题.

2.1 含90°对角互补模型

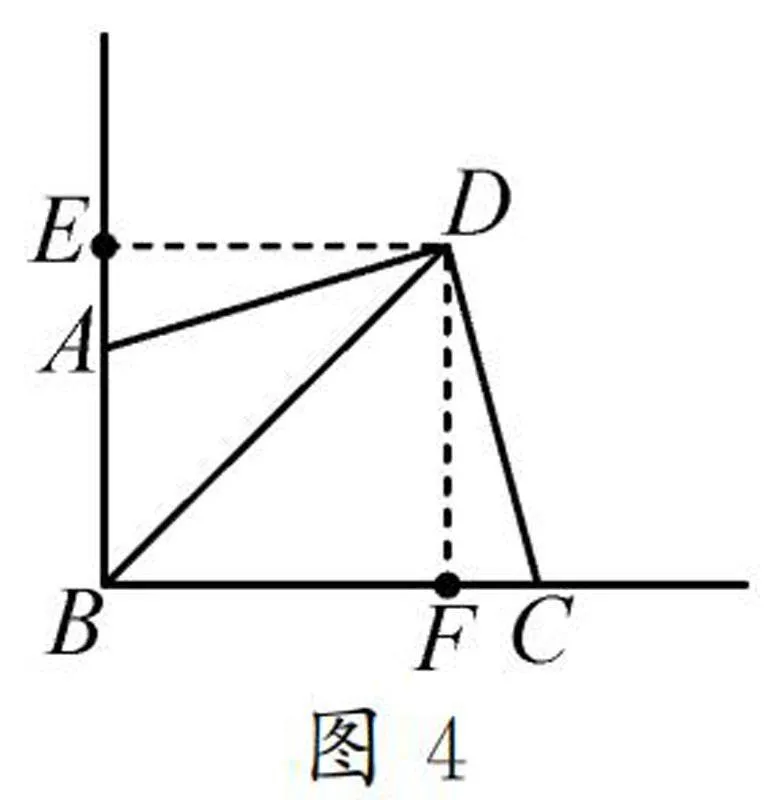
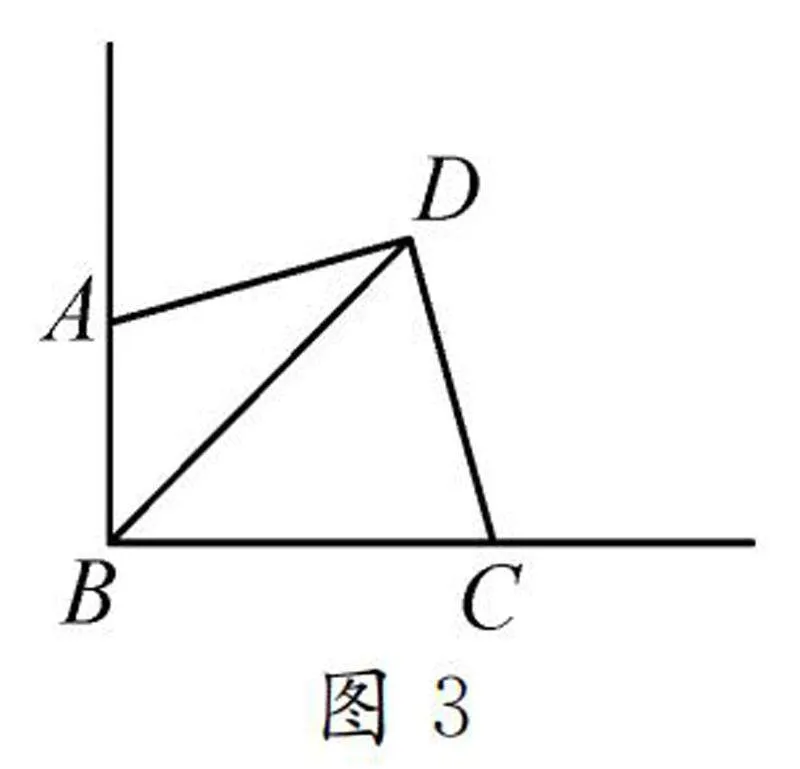
如图3，已知∠ABC=∠ADC=90°，AD=DC，则可得：①BD平分∠ABC；②AB+BC=2BD；③S=S+S=1/2BD2.

证法一：过顶点作双垂线证明.

①如图4所示，过点D作DE⊥EB，DF⊥BC，垂足分别为E，F.

∴∠DEA=∠DFC.

∵∠ABC=∠ADC=90°，

∴∠DAB+∠DCB=180°.

∵∠DAB+∠DAE=180°，

∴∠DCB=∠DAE.

∵AD=DC，

∴△DEA≌△DFC.

∴DE=DF.

∴四边形DEBF为正方形.

∴∠ABD=∠DBC.

∴BD平分∠ABC.

②∵四边形DEBF为正方形，

∴BD=2EB=2BF.

③∵△DEA≌△DFC，

∴S=S+S=S+S+S=S=1/2BD2.

证法二：旋转法证明.

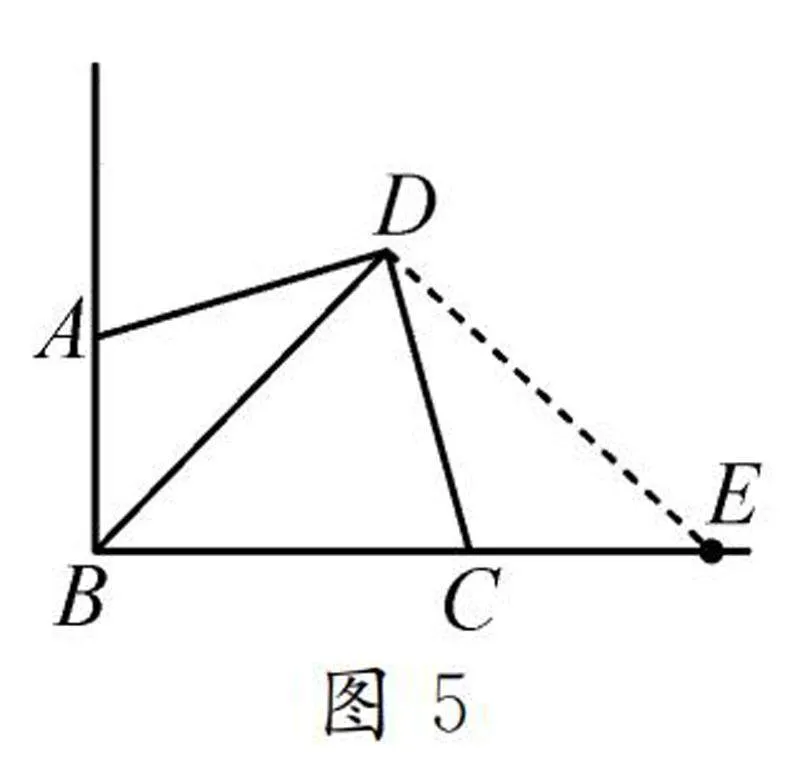
图5①如图5，将△DAB绕点D逆时针旋转，当AD与DC重合时，点B落在射线BC上的点E处.

∴△DAB≌△DCE.

∴∠ADB=∠CDE.

∵∠ADB+∠BDC=90°，

∴∠BDC+∠CDE=90°.

∴∠BDE=90°.

∵DB=DE，

∴△BDE为等腰直角三角形.

∴∠DBC=45°.

∴BD平分∠ABC.

②∵AB=CE，

∴BC+CE=BC+AB=2BD.

③∵△DAB≌△DCE，

∴S=S+S=S+S=S=1/2BD2.

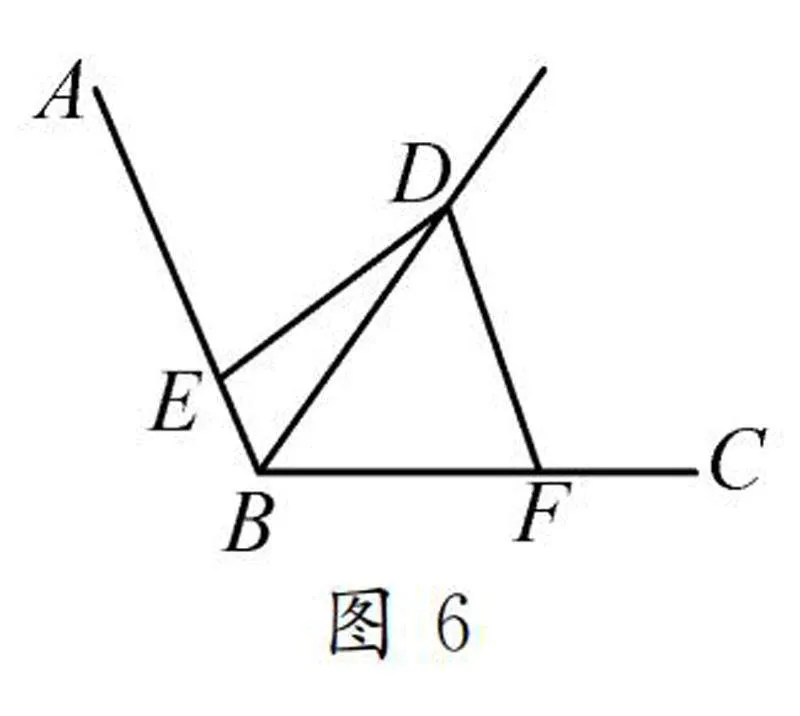
2.2 含120°对角互补模型

如图6所示，已知∠ABC=2∠EDF=120°，DE=DF.

结论：①BD平分∠ABC；②EB+BF=BD；③S+S=34BD2.

3 对角互补模型复习策略

3.1 基础知识梳理

为了更有效地复习、掌握对角互补模型，学生需要对相关的基础知识进行梳理和强化.首先，学生需要深入理解角的互补性质，这是对角互补模型的基本前提.其次，学生应熟练掌握平行线的性质，如平行线间的同旁内角互补、内错角相等、同位角相等，因为这些性质与对角互补模型有着密切的关系［1］.此外，相似三角形和全等三角形判定条件也是复习的要点.因为在对角互补模型的解题过程中，经常需要利用这些判定条件来证明三角形的相似或全等，从而找到解题的突破口.为了更有效地复习这些基础知识，学生还可以采取制作思维导图、编写知识卡片等方式，将知识系统化、条理化，便于记忆和回顾.除了上述的基本知识点，学生还需要对与对角互补模型相关的定理、公式进行系统回顾和整理.例如，勾股定理、三角函数等，这些定理和公式在解决对角互补模型问题时经常会被用到.通过复习这些定理和公式，学生可以更好地理解和应用对角互补模型.

3.2 模型思维训练

在掌握了基础知识后，学生应当进行深入的模型思维训练.这不仅意味着要识别出题目中蕴含的对角互补模型，更要深入理解模型的本质及其所蕴含的几何规律.通过大量的练习和模拟，学生能够在脑海中建立起对角互补模型的清晰图象，提高对这种模型的敏感度.当遇到相关题目时，学生能够迅速形成条件反射，联想到对应的模型和解题策略，从而高效、准确地解答问题.这种训练不仅有助于提高学生的解题速度，还能帮助他们形成更为系统的几何思维模式［2］.

3.3 解题思路内化

解题思路的内化对于提高解题能力至关重要.学生首先需要深入理解并掌握对角互补模型的解题思路和方法，如巧妙地构造辅助线，准确地运用相似三角形和全等三角形的性质等.在解题的过程中，学生应当注重思路的连贯性、条理性，确保每一步都有充分的依据和明确的目的.为了加深理解，学生应不断进行练习和反思.通过反复实践、思考，学生可以将这些解题思路、方法逐步内化为自己的思维习惯.这样，在面对类似的问题时，学生便能迅速并准确地找到解题的切入点，从而提高解题的效率和准确性.这一过程不仅有助于提升学生的数学能力，更能培养学生严谨的逻辑思维和自主学习能力［3］.

3.4 练习与反馈

练习是提高解题能力的重要途径.在复习对角互补模型的过程中，学生需要通过大量的练习来加深理解.同时，学生应注重练习的质量和效果，选择具有代表性的题目进行练习，并及时反馈练习情况.通过练习，学生可以了解自己的不足和需要改进的地方.这时，学生可以向老师请教或与同学交流讨论，以获得更好的指导和建议.在练习过程中，学生还应注重错题的总结和归纳.通过整理和分析错题，学生可以找出自己的薄弱环节和易错点，并制定相应的改进措施.这样可以帮助学生更好地巩固知识点和提高解题能力［4］.

4 结论

对角互补模型是初中数学几何部分的重要知识点之一，它涉及角的互补性质、相似三角形、全等三角形的判定条件等多个方面.通过掌握相关的解题方法和策略，学生可以有效地提高解决此类问题的能力.因此，在复习过程中，学生应重视对角互补模型的学习和练习，加强基础知识的掌握，通过不断练习提升自己的思维能力和应用能力.

参考文献：

[1]苏锡永.浅谈数学教学与高阶思维能力培养[J].考试周刊，2023（12）：69-72.

[2]刘海燕.初中数学建模思想初探[J].现代教育科学，2011（4）：126-128.

[3]张细婷.关于中考数学复习方法与策略的探索[J].学周刊，2015（20）：198.

[4]吕凤艳.基于中考导向的初三数学复习课教学探究[J].辽宁教育，2022（1）：89-92.